直驱风电场多电压源型变流器控制耦合引发振荡的机理分析

郑泽天，沈 沉，严 鋆，袁沐琛，刘 晔，范 辉

（1.清华大学电机工程与应用电子技术系，北京市 100084；2.中国电力科学研究院有限公司，北京市 100192；3.国网河北省电力有限公司，河北省 石家庄市 050022）

0 引言

新能源系统的发展依赖于电力电子设备的发展与应用［1］，而高比例电力电子设备的应用也导致电网稳定性问题愈发严重。其中，电磁振荡极大影响了风电系统的发展。典型的电磁振荡事故有中国河北沽源的双馈风电场次同步振荡事故以及新疆哈密的直驱风电场次/超同步振荡事故［2-4］。这些事故都造成了大量发电机脱网以及各方面经济损失，有些地区至今仍可频繁监测到次同步电流，为风电场的建设和并网埋下安全隐患。与双馈风机相比，直驱风机的电力电子化特征更加明显，同时也更容易引发风电系统的振荡问题［5］。因此，本文以直驱风机风电场为对象，对相关电磁振荡问题进行研究。

现场录波数据显示，实际风电系统中的电磁振荡往往可分为2 个阶段：第1 阶段，系统因参数配置失当、控制方式切换或运行方式改变，导致系统存在至少一个右半平面特征根，由不稳定模式引发的电磁振荡始于系统平衡点附近的发散振荡；第2 阶段，并网变换器控制系统中的限幅环节饱和，振荡不会持续发散，最终形成等幅自持振荡［6］。

对于第1 阶段中产生发散振荡触碰限幅的诱因，现有文献往往假设单机内外环控制参数设置不当［7］。本文认为单机出厂时其参数已经根据相关并网导则进行过整定，运行时出现因单机控制参数配置失当而产生不稳定模式的概率较低。同时，风电系统中有较多电压源型变流器（voltage source converter，VSC）设备，如直驱风机和静止无功发生器（static var generator，SVG）等，运行中可能存在相互作用。因此，本文主要考虑运行中多VSC 产生耦合作用、控制方式切换或运行方式改变导致第2 阶段等幅自持振荡的可能性。

SVG 被广泛安装在现代风电系统中，主要用于改善电压稳定的问题。然而，SVG 与风电场之间可能存在电磁相互作用。为研究SVG 和直驱风电场的耦合作用，首先要对SVG 进行建模。常见的模型为线性化模型。例如，文献［8］将SVG 建模为一个受控电流源；文献［9］通过推导SVG 以及直驱风机的线性化模型，获得输入阻抗模型以及并网系统的传递函数；文献［10］采用谐波线性化方法建立SVG的正负序阻抗模型，以此来研究SVG 的接入对系统稳定性的影响。然而，上述文献均将SVG 作为独立装置单独建模，忽略了其与直驱风机控制结构的相似性，不利于共性振荡机理的挖掘和归纳。

针对SVG 与风电场之间交互机理的研究，目前已取得一定成果。文献［11］研究了含SVG 的双馈风电场次同步振荡问题，研究结果表明振荡是由限幅环节引起的切换型次同步振荡现象，并进一步研究了SVG 不同控制参数对于系统振荡的影响。文献［12］揭示了双馈风电机组转子侧变流器控制参数以及SVG 控制参数对于振荡的影响。文献［13］研究了SVG 与双馈风电场之间次同步振荡的相互作用机理。文献［14］推导并构建了基于dq解耦控制的SVG 控制策略和仿真模型，研究基于直驱风机的风电场中SVG 对次同步振荡的影响。文献［15］建立了双馈感应发电机和SVG 的序阻抗模型，并基于伯德图的稳定性准则和时域仿真，分析了SVG 的接入对次同步振荡的影响。

上述研究均局限于单台SVG 与风电场之间的耦合影响。而针对多台SVG 之间耦合作用引起的振荡、SVG 不同控制方式对多台SVG 之间振荡的影响，以及SVG 耦合振荡引起风电场自持振荡的可能性尚未见报道。

本文考虑直驱风机和SVG 的共性特点，从统一的VSC 控制系统建模出发，建立了适用于电磁振荡研究的双VSC 耦合系统模型，分析了不同电气距离的双VSC 发生耦合作用时，系统产生不稳定模式的机理，进一步研究了电网侧连接电抗的变化（即系统强弱变化）对出现发散振荡的概率的影响。最后，通过仿真验证了所提振荡机理的正确性。本文同时指出，上述振荡机理可能成为导致风机发生限幅非线性自持振荡的外因。

1 用于电磁振荡研究的风电场建模

考虑到风电场中的直驱风机和SVG 设备有相似的VSC 结构，本章通过简化风机结构，尝试用统一的VSC 控制系统结构对2 种设备进行建模。

1.1 风电场并网模型和典型直驱风机结构

一个典型的直驱永磁同步发电机（permanent magnet synchronous generator，PMSG）风电场包含30～60 台风机。一般而言，几台直驱风机连接在一起形成一个串型结构，而几“串”风机又通过公共连接点（point of common coupling，PCC）经过一系列升压变压器和输电线路（相当于一组阻抗）连接到35 kV 电压等级主网［16］，如图1 所示。图中：每个串型结构中含有n台直驱风机。图2 为典型直驱风电机组的示意图。

图1 风电场接入电网的模型Fig.1 Model of wind farm connected to power grid

图2 典型直驱风电机组结构Fig.2 Structure of typical direct-driven wind turbines

与机侧机械部分强相关的振荡模式即为轴系扭振模式，其振荡频率在低频振荡频段［17］，而控制耦合相关电磁振荡在次同步或超同步频段［18］。直驱风机的永磁同步发电机与电网完全解耦，且机侧变流器采用最大功率跟踪控制。因此，其与电网的交互较小，机侧的振荡模态也很难影响风机网侧输出特性。相关研究表明，直驱风机与电网之间［19-20］以及多直驱风机之间［21］的控制耦合作用引起的振荡模式和直流电容动态以及网侧变流器控制强相关，而与风力机、发电机动态以及机侧变流器控制相关性较弱。因此，机侧部分（包括风力机、发电机和机侧变流器）在建模时，可等效为一个由风力机接收风功率并转化为电功率的功率源；包含直流电容的网侧变流器d轴控制回路保持直流母线电压稳定，q轴控制回路保持输出无功功率稳定，可被建模为具有对应控制系统的VSC。

1.2 统一的VSC 控制系统建模

本文考虑的SVG 模型采用双闭环反馈控制。d轴控制回路保持直流母线电压稳定，q轴控制回路则有不同的控制模式：当SVG 为恒电压控制时，q轴的控制目标是端电压；当SVG 为恒无功控制时，q轴的控制目标是输出的无功功率。由此，可建立直驱风机风电场中直驱风机和SVG 统一的VSC 控制系统，仅需要改变q轴的控制目标就可以在不同情况之间切换，如图3 所示。图中：vdc和分别为直流母线电压的量测值和参考值；C为直流电容；vd、和Q、分别为机端电压d轴分量和输出无功功率的量测值、参考值；vq为机端电压q轴分量的量测值；va、vb、vc和ia、ib、ic分别为机端电压和输出电流的三相量测值；id和iq分别为输出电流量测值的d轴和q轴分量；和分别为输出电流参考值的d轴和q轴分量；v′、v、vpcc、vg分别为变流器输出、机端、PCC处、电网接口的相电压；V为机端相电压幅值；和分别为脉宽调制（pulse width modulation，PWM）参考电压的d轴和q轴分量；θ为锁相环（phase locked loop，PLL）输出相角；R、L和R2、L2分别为VSC 输出和机端之间的滤波电阻、电感；Rl1、Ll1和Rl2、Ll2分别为机端和PCC 之间变压器和输电线路的等效电阻、电感；Rg和Lg分别为PCC 和电网之间输电线路的等效电阻和电感；ω0=2πf0为角频率，其中，f0为工频。

图3 VSC 控制系统结构Fig.3 Structure of VSC control system

2 双VSC 耦合系统建模

为研究风电场中VSC 相互耦合产生发散振荡的机理和触碰限幅的诱因，本章对限幅产生作用前的双VSC 耦合系统进行建模。

以定向到无穷大母线电压相量上的同步旋转坐标系dq0 为全网公共坐标系，列写网络方程并线性化得：

式中：下标1、2 分别对应VSC1和VSC2；v′d和v′q分别为变流器输出电压的d轴分量和q轴分量；vpccd和vpccq分别为PCC 处电压的d轴分量和q轴分量；s为复变量；Δ 表示变量与平衡点的偏差量。

对于外环直流电压控制，根据功率守恒并线性化得：

研究SVG 动态时，d轴直流电压外环控制回路比例-积分（PI）环节的方程为：

式中：Gdc1，2(s)为d轴外环PI 环节的传递函数。

q轴外环控制回路PI 环节的方程为：

式中：Gv1，2(s)为q轴外环PI 环节的传递函数。

如图3 所示，研究直驱风电机组动态时，只需将式（6）改为：

统一的电流内环控制回路PI 环节方程为：

式中：Gi1，2(s)为电流内环PI 环节的传递函数；上标c 表示电气量定义在SVG 内部PLL 定向的dq0 坐标系。

对于该坐标系下某一电气量的d轴和q轴分量和，将其变换到全网公共坐标系下得到电气量xd和xq，变换方程为：

式（9）中，Δθ1，2可由PLL 的动态进行计算：

式中：GPLL1，2(s)为PLL 环节的传递函数。

3 双VSC 耦合产生不稳定模式的机理分析

本章首先讨论稳态情况下VSC 机端近似条件，然后，化简得到双VSC 在不同电气距离和不同控制目标下的网络方程，并按化简结果的不同分为3 种情况：1）双SVG 电气距离较近；2）双直驱风机电气距离较近；3）双VSC 电气距离较远（此时，SVG 与直驱风机化简结果一致）。

本章主要讨论前2 种情况下VSC 因动态耦合产生不稳定模式的机理。对于第3 种情况，当2 个VSC 电气距离较远时，它们到PCC 的连接阻抗较大，相互耦合作用较小。单机低短路比情况下不稳定模式的产生机理已有较多文献开展了研究［22-23］，本章将使用耦合模型进行简单验证，以证明所提机理与文献中结论的统一性。

3.1 稳态情况下VSC 机端电气量近似关系

为分析双VSC 耦合系统的不稳定趋势，先对其端口电气量的关系进行推导。由于仅对其作原理性的解释，为分析简便，假设线路仅有连接电抗而没有连接电阻，即Rl1，2=0。

1）SVG

稳态情况下认为SVG 发出有功功率为0，即P1，2=0。将定电压控制的SVG 视为PV节点，定无功控制的SVG 视为PQ节点，从潮流计算近似可得：

2）直驱风机

稳态情况下认为直驱风机发出无功功率为0，即Q1，2=0。将直驱风机视为PQ节点，从潮流计算近似可得：

以上分别得到了SVG 和直驱风机对应的机端近似条件。

3.2 网络方程化简

由式（2）和式（3）可得：

式（13）即为系统网络方程，以下讨论不同情况下式（13）的化简结果。

3.2.1 双SVG 电气距离较近情况下的网络方程化简

将式（11）代入式（13），又根据假设Rl1，2=0，则当Ll1，2→0 时，式（13）可化简为：

设x=Δiq1+Δiq2，对式（14）的第2 行公式做反拉式变换（假设初始值为0），有

解得：

稳态时，可认为Δiq1+Δiq2=0，后文在对其他电气量进行类似讨论时将不再另行说明，都取该电气量的稳态值为0。

将Δiq1+Δiq2=0 代入式（14）的第1 行公式得Δvd1，2=0。

综上可得：

以上结论是在SVG 发出无功功率为0 且2 台SVG 都与PCC 电气距离足够近这2 个条件下，根据网络方程得出的，与SVG 本身的控制无关。由上述讨论可知，此时SVG 端口的电压和电流被“钳位”，几乎没有调节余地，Δiq1和Δiq2仅有一个自由度。

进一步，对网络方程式（2）、式（3）线性化前的微分方程进行类似分析。式（17）将变为：

3.2.2 双直驱风机电气距离较近情况下的网络方程化简

将式（12）代入式（13），又根据假设Rl1，2=0，则当Ll1，2→0 时，式（13）可化简为：

由式（19）的第2 行公式可得Δid1+Δid2=0，代入式（19）的第1 行公式得Δvd1，2=0。

综上可得：

与双SVG 的网络方程式（17）相比较，自由度从q轴电流转移到了d轴电流。

3.2.3 双VSC 电气距离较远（包含SVG 和直驱风机）情况下的网络方程化简

对于双SVG，将式（11）代入式（13）；对于双直驱风机，将式（12）代入式（13）。 同时，考虑Rl1，2≫Rg、Ll1，2≫Lg可得：

综上，式（17）、式（20）和式（21）分别对应网络方程的3 种不同情况，下面也将分别在这3 种情况下对双VSC 耦合产生不稳定模式的机理进行分析。

3.3 不稳定机理分析

上节推导得到了式（17）、式（20）和式（21），其表达了不同情况下VSC 外部网络中电气量在稳态时需要满足的条件。本节将在此基础上推导控制系统内部状态变量的平衡点，并讨论不同情况下该平衡点的稳定性。

3.3.1 电气距离较近时的双SVG 系统将式（17）代入式（1）、式（4）—式（9），有

此时，化简后的系统不再包含某些dq控制回路，如图4 所示。图中：反馈回路由蓝色箭头表示，相关电气量变化趋势由红色箭头表示。

图4 电气距离较近时的双SVG 系统Fig.4 Double-SVG system with short electrical distance

考虑系统的稳态平衡点。若SVG 采用定机端电压控制，令参考量设定值=0，由式（17）有Δvd1，2=0；若SVG 采用定无功控制，令参考量设定值=0，而ΔQ1，2=+=0。代入式（6），2 种控制方式均有：

当某台SVG 的Δvdc或Δv因任何扰动首先发生变化时，因为电感上的电流不会突变，所以应该先分析其本身控制回路的变化，再分析外电路的电气量变化。而另一台SVG 则先由外电路耦合的电气量发生变化，再影响其控制回路。

假设对系统施加微小扰动，不失一般性，不妨假设SVG1首先感受到扰动，Δvdc1＞0。

1）考虑d轴控制回路

由式（26）可得Δvdc1＞0 时，＞0，由式（23）可得Δv′d1＞0、Δiq1＜0、Δv′q1＜0，又Δiq1+Δiq2=0，则Δiq2＞0、Δv′d2＜0，使得Δiq2更大，从而使Δiq1更小，形成正反馈，系统失稳，直到某一处限幅环节作用为止。

2）考虑q轴控制回路。

若2 台SVG 中至少有一台为定无功控制，不失一般性，不妨假设SVG1采用定无功控制，则有：

当Δiq1＜0 时，ΔQ1＞0、＞0、Δiq1＞0，形成负反馈。此时，在控制参数合适的情况下，系统可以稳定。

若2 台SVG 都是定电压控制，不失一般性，假设SVG1首先对扰动开始响应。由式（17）可知，Δvd1已经由外电路钳位至0，q轴控制回路对iq1实际没有控制能力，最终系统因d轴正反馈失稳。

记Gv1，2(s)=Gkp1，2+Gki1，2/s，其中，Gkp1，2和Gki1，2分别为该PI 环节的比例系数和积分系数。式（6）的第1 行公式对应线性化前的微分方程为：

3.3.2 电气距离较近时的双直驱风机系统

将式（20）代入式（1）、式（4）—式（9），有

与3.3.1 节同理可得此时所有偏差量均为0，系统处于平衡点，对平衡点稳定性进行分析。假设对系统施加微小扰动，不失一般性，不妨假设PMSG1首先对扰动开始响应。例如：Δvdc1＞0，则由式（34）可得＞0，由式（31）可得Δv′d1＞0、Δid1＞0、Δv′q1＞0，又Δid1+Δid2=0，则Δid2＜0、Δv′d2＞0，使Δid2＞0，从而使Δid1＜0，形成负反馈，系统可以稳定，如图5 所示。

图5 电气距离较近时的双PMSG 系统Fig.5 Double-PMSG system with short electrical distance

3.3.3 电气距离较远时的双VSC 系统（包含SVG和直驱风机）

将式（21）代入式（1）、式（4）—式（9），状态变量偏差量全部为0，系统处于平衡点。分析可得，此时对其中一台VSC 施加微小扰动，该扰动引起的VSC 控制系统内部电气量变化通过耦合作用对另一台VSC 产生的影响较小。此时，系统的不稳定模式可能来源于单台VSC 与弱电网间的相互作用，不是由两机控制的耦合作用产生。该平衡点仍为不稳定平衡点，但该情况不是本文讨论重点，不再赘述。

3.4 小结

根据本节分析，各种情形总结如表1 所示，对双VSC 耦合有以下结论：

表1 双VSC 的耦合作用Table 1 Coupling effects of double-VSC

1）2 台SVG 电气距离较近且都采用定电压控制时，判断电压参考值匹配判据为=vg且=vg，若不满足则可能产生不稳定振荡模式。当至少有一台SVG 采用定无功控制时，系统可以稳定。

2）一台SVG 和一台直驱风机电气距离较近时，由于直驱风机本质上工作在定无功控制模式，无论SVG 采用何种控制，两机系统不会形成正反馈，系统可以稳定。

3）2 台直驱风机电气距离较近甚至直接并联时，系统稳定（单机控制参数合理）。

4）2 台VSC（包含SVG 和直驱风机）电气距离过远时，两机控制耦合的交互作用较弱。系统此时仍有可能出现不稳定模式，如文献［22-23］所述的单机低短路比情况下与电网相互作用产生的次同步振荡，该情况不属于本文讨论范围，故不再赘述。

4 考虑随机性的发散振荡概率计算方法

由第3 章可知，双SVG 控制耦合引发的振荡与电气距离远近紧密相关。本章将距离远近量化为连接电抗大小进行研究。考虑到系统侧运行方式的变化，包括串补投切等操作引起的系统等效连接电抗变化较为复杂，难以显式表达。因此，本章将等效电抗的大小看成随机数，并假设其服从某一分布，进而推导等效电抗变化时发散振荡发生概率的计算方法。

4.1 考虑随机性的电力系统特征量计算方法

考虑系统内一组W维随机变量X，其波动会影响选定的特征量Y，两者间存在隐函数关系：

式中：h(·)为一般的非线性函数，Y与X间无显式表达式。

现假设已知X的分布，要求Y的分布，则将式（35）在平衡点X=X0处做泰勒展开，保留二阶项，有

其中，

式中：Xi为自变量的第i个元素；n为元素总数。

灵敏度矩阵Δ和海森矩阵Γ可采用摄动法计算得到：

式中：ΔXi为Xi的微小增量。

高斯混合模型（Gaussian mixture model，GMM）可以将任意随机分布的概率密度函数描述为一组高斯分布概率密度函数的加权和。取X͂=X-X0，W维随机变量X͂的概率密度函数可用GMM 描述为：

式中：fX͂(X)为多维随机变量X͂的联合概率密度函数；Nm(X|μm，Σm)为一个以μm为均值向量、Σm为协方差矩阵的多维高斯分布；M为GMM 中高斯分量的项数；ωm为第m个高斯分量的权重。

文献［24］给出了一种形如随机变量函数的计算方案如下：

式中：θ0为任意常数。

假设已知X的分布，将随机变量X͂=X-X0写成如式（39）的GMM 形式，并利用GMM 的叠加性，可以计算函数Y的分布［25］。

4.2 连接电抗大小随机变化时发散振荡发生概率的计算方法

考虑图3 中2 台VSC 到PCC 和PCC 到主网的连接阻抗构成星形结构，可作星形-三角形变换，如图6 所示。

图6 连接阻抗的星形-三角形变换Fig.6 Star-delta transformation of connection impedance

图中：

式中：Zline1、Zline2为2 台VSC 到PCC 的连接阻抗；Zg为PCC 到主网的连接阻抗；Z12、Z13、Z23为变换后的阻抗，呈三角形地连接在各端口之间。

当双 SVG 电气距离较近时，可认为Zg≫max{Zline1，Zline2}，则有Z12≪min{Z13，Z23}。因此，可近似只考虑Z12对系统振荡的影响。进一步，主网中投切串补等改变系统运行方式的操作引起Zg变化，由式（41）可考虑为Z12的变化。考虑到系统运行方式变化导致Z12呈现的任何分布均可使用GMM 拟合，同时，不同X的分布在GMM 形式下对应特征量Y的数学表达也具有一致性。因此，在没有Z12先验分布信息的前提下，本文仅为说明机理，不妨认为其满足均匀分布。

对于式（35），取X为双SVG 的连接电抗，取Y为系统主导特征根的实部，按照4.1 节方法进行计算，即可得到连接电抗大小随机变化时主导特征根实部的分布函数，可反映双SVG 发生发散振荡的概率。在算例分析部分，将结合具体参数和仿真结果，对所研究场景中等效连接电抗随机变化时双SVG发生发散振荡的概率进行计算和分析。

5 算例分析与讨论

5.1 两台SVG 的耦合振荡

按照图3 所示的结构建立2 台SVG 耦合并网系统，其中，SVG 模型及其控制参数如表2 所示。

表2 SVG 仿真参数设置Table 2 Simulation parameter configuration for SVG

根据式（1）—式（10）列写系统状态空间方程，并计算不同情况下的系统特征根，其分布情况如图7所示。图7（a）中2 台SVG 均为定电压控制，机端电压参考值的标幺值=1.000，=1.005，SVG2不满足3.4 节中电压参考值匹配判据，系统出现一对（2 个）不稳定共轭复根。图7（b）中，2 台SVG 均为定电压控制，=0.995=1.005，2 台均不满足电压参考值匹配判据，系统出现4 个不稳定实根。通过计算各特征根中状态变量的参与因子，可得到不稳定模式对应的强相关变量，如表3 所示。由表3可知，与系统主导不稳定模式强相关的状态变量是SVG 的电流和d轴机端电压对应的状态变量；对该组动态特性影响明显的控制参数应为机端电压参考值。

表3 不稳定模式对应的强相关变量Table 3 Strongly correlated variables corresponding to unstable modes

图7 不同情况下的系统特征根Fig.7 System eigenvalues in different conditions

图7（c）和（d）的特征根均在虚轴左侧，表明2 台SVG 中至少一台为定无功控制时，在合理参数下系统可以稳定，与第3 章中的机理与结论相吻合，证明了其正确性。

在PSCAD 中建立由2 台SVG 背靠背连接并接入无穷大电网的系统详细模型，其控制和系统参数如表2 所示。仿真设置如下：

t=2 s 时，SVG2接入电网，设为定电压控制，设定其机端电压参考值=1.005；t=5 s 时，SVG1接入电网，设为定电压控制，设定机端电压参考值==1；

t=10 s 时，设定SVG2机端电压参考值=1.005；

t=15 s 时，设定SVG1机端电压参考值=0.995；

t=20 s 时，将SVG1变为定无功控制，设定SVG1无功功率参考值=4 MW；

t=25 s 时，将SVG2变为定无功控制，设定SVG2无功功率参考值=4 MW。

SVG2在t=2 s 后全程接入电网，因此，选取SVG2的相关波形展示仿真结果，如图8 所示。以5 s为间隔，共分为6 段，分别对应2 台SVG 不同q轴的控制组合情况。观察仿真结果可知，当2 台SVG 均为定电压控制且不满足电压参考值匹配判据时，系统会存在不稳定模式（发散振荡），当电压外环PI 的限幅环节起作用时，形成自持等幅振荡。通过Prony 分析可知，该振荡频率为29.85 Hz，在次同步频段范围内。SVG2电压外环PI 输出的电流参考值和如图9 所示。2 台SVG 电压参考值均不匹配时，电流参考值的直流偏移较大，造成其“削头”程度较大。因此，机端观察到的振荡幅值反而比2 台SVG 中仅有一台SVG 电压参考值不匹配时的振荡幅值略小。而当至少一台SVG 选取定无功控制时，振荡平息。仿真结果与机理分析和模式计算结果一致。

图8 SVG2直流电压、机端电流、机端电压的仿真结果Fig.8 Simulation results of DC voltage, terminal current and terminal voltage of SVG2

图9 SVG2电流参考值波形Fig.9 Current reference waveforms of SVG2

如4.2 节所述，考虑电网侧投切串联补偿电容引起的连接电抗变化，串补度k一般不超过50%［26-27］。式（41）改写为：

忽略线路电阻，各条线路的连接电感仍按表2取值，取k的范围为0 ≤k≤50%，则等效连接电抗L12的取值范围为0.202 mH ≤L12≤0.204 mH，可见串补对等效连接电抗的影响较为有限。为包含故障切机和其他改变运行方式操作产生的极端情况，将L12的变化范围放大，考虑为0～0.4 mH 的均匀分布。2 台SVG 均设置为定电压控制，且均不满足电压参考值匹配判据，按照4.1 节所述步骤进行计算，特征量Y为系统主导特征根的实部，其分布函数如图10 所示。可见，当等效连接电抗随机变化时，主导特征根变化范围较大，但始终在虚轴右侧，进一步证明了电气距离较近时本文所提出的系统不稳定机理的正确性。

图10 所选特征量的概率密度分布Fig.10 Probability density distribution of selectedcharacteristic quantity

5.2 含SVG 的直驱风机风电场耦合限幅振荡

进一步，考虑2 台SVG 耦合作用引起风电场自持振荡的可能性。如图11 所示，在PSCAD 中建立双直驱风机风电场模型，风电场出口分别连接SVG，且SVG 控制参数和系统参数设置均不变，如表2 所示。直驱风机的仿真参数如表4 所示。本算例仅从原理方面说明振荡发生的可能性。因此，每个风电场只设置一台等值直驱风机。

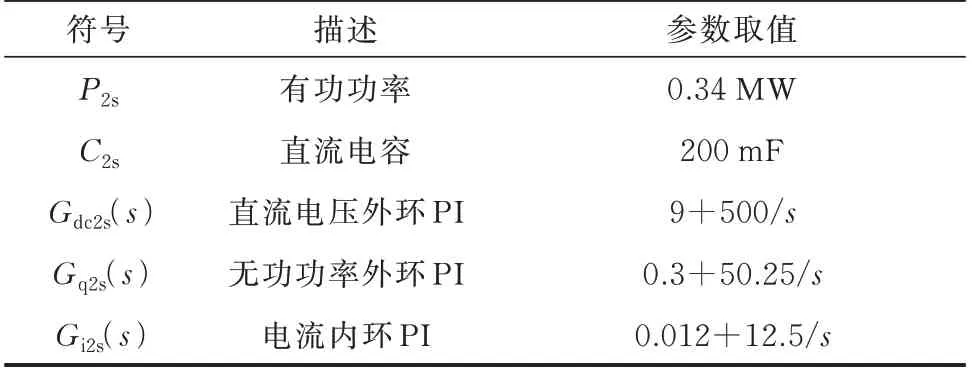
表4 单台PMSG 仿真参数设置Table 4 Simulation parameter configuration for single PMSG

图11 含SVG 的双PMSG 风电场模型Fig.11 Double-PMSG wind farm model with SVGs

仿真设置与5.1 节完全相同，仍可按SVG 不同情况分为6 段，仿真结果如图12 所示。图8 和图12中，SVG2直流电压的波形几乎完全一致。事实上，直驱风机的接入并没有对SVG 中各电气量的波形和性质产生影响。但是，观察图12 中PMSG2电流参考值和直流电压可知，t=2 s 时直驱风机接入电网后，经过过渡过程可以稳定。t=10 s 时，2 台SVG因定电压控制产生耦合振荡，激发了直驱风机的不稳定模式，最终d轴电压外环PI 的限幅环节起作用，形成等幅自持振荡。t=20 s 后，即使SVG 定无功控制后已经退出振荡回到稳定状态，直驱风机也因满足自持振荡条件（可通过基于描述函数扩展的Nyquist 定理判断［28］）而维持等幅振荡，不受SVG 控制策略和运行方式改变的影响。

图12 SVG2直流电压、PMSG2电流参考值和直流电压的仿真结果Fig.12 Simulation results of DC voltage of SVG2,current reference and DC voltage of PMSG2

6 结语

本文将风电场中的直驱风机和SVG 统一建模为VSC 控制系统，详细分析了双VSC 耦合下不同电气距离情况产生不稳定模式的机理，提出了连接电抗大小随机变化导致系统发生振荡的概率计算方法。机理分析和算例验证表明，2 台SVG 电气距离较近且都是定电压控制时，需要根据电压参考值匹配判据判断系统是否会发生振荡。若判据不满足，则系统存在不稳定模式，该模式对投切串补等改变运行方式的操作敏感度较低，仅能通过改变控制方式消除振荡。

本文还提出一种非线性自持振荡机理，即直驱风机在初始状态下可稳定运行，但SVG 耦合产生的不稳定模式可能激发等幅自持振荡，且自持振荡被激发后可不依赖于SVG 的振荡状态而持续维持。此时，直驱风机的限幅自持振荡形成了一种“本地模式”，SVG 切换控制策略后自身稳定运行，而其运行方式的改变也不再影响直驱风机的自持振荡状态。这种由外因引发且外因撤去后仍能保持的自持振荡现象在热力学领域时有发生［29］，但在电力系统中尚无相关研究。该机理说明，在工程中需要对事故全程更精确、更全面地分析，而不能仅仅将振荡源定位于观察时刻正在振荡的机组，否则可能得到错误的振荡机理。

本文仅从原理出发说明控制耦合振荡发生的机理，对于更复杂的多VSC 耦合场景尚无法得到解析结果，可考虑结合动态等值方法和电磁暂态仿真进行进一步研究。