基于多域融合的空间辐射源细微特征识别

2023-09-18王晓晗闫毅范亚楠李雪牟娇

中国空间科学技术 2023年4期

王晓晗,闫毅,范亚楠,李雪,牟娇

1.中国科学院国家空间科学中心,北京 100190

2.中国科学院大学,北京 100049

1 引言

辐射源个体识别在电子对抗和通信安全等方面起到至关重要的作用,是非合作通信侦察中的一项关键技术[1]。辐射源识别主要根据所截获射频信号的差异判断所属辐射源[2],根据辐射源工作状态掌握其载体的情况,从而有针对性地对其进行监视和管理[3-4]。卫星通信不受地域地形的限制,具有通信距离远、全球覆盖、安全可靠的优势,研究空间辐射源识别技术,对通信卫星的有效的侦察、监测和管理具有重要意义。

由于辐射源设备的个体差异,在信号上不可避免地存在着不影响信息传递的细微特征差异,这些可检测、可重现的细微差别被称为信号细微特征或辐射源个体细微特征[5]。射频设备中电子元件的容差是形成细微特征的原因,元件在生产时实际值与标称值存在差异,在工作过程中温度、湿度、老化也会引起参数的变化。目前认为,空间辐射源细微特征的主要成因是卫星转发器中功率放大器的非线性效应[6]。通信卫星与地面站的距离遥远,为了抵消路径损耗,保证功率放大器较高的工作效率,卫星转发器中的功率放大器通常工作在饱和状态或邻近饱和状态,导致输出的信号产生严重的非线性失真。由放大器产生的非线性产物主要有谐波、交调、互调和杂散等[7-9]。因此,由于元件容差的存在,系统的非线性特性不同,对信号的影响也随之不同,这给依据信号中提取细微特征,进而识别出相应的辐射源个体提供了可行性。

目前,国内外针对辐射源识别问题,主要针对暂态信号与稳态信号两类信号进行研究。暂态信号是指辐射源在开、关机和模式转换时由于工作状态不稳定所产生的能体现辐射源特征的信号,因其持续时间短且受噪声干扰影响大,不易于进行辐射源识别。稳态信号是指辐射源稳定工作时所辐射的信号,存在于整段信号的信息中,易于获取并且能够更全面描述发射机信号的特征,因此是辐射源识别的研究重点。

近年来,众多学者针对稳态信号的提取提出了多种处理方法,主要包括贝叶斯估计[10]、信号包络[11]、二维时频特征[12]、Wigner-Ville分布[13]、小波变换[14]、固有时间尺度分解[15]、变分模态分解[16]、Hilbert-Huang变换[17-18]、双谱分析[19-21]等理论。文献[22]利用雷达信号的累积量作为个体识别的特征,使用KNN分类器对3部同型号机载雷达的实测数据进行分类识别,取得良好的分类效果。文献[23]使用离散傅里叶变换的功率谱构建了谱域特征,结果表明谱域特征比时域特征性能好,与小波域特征性能接近,并略有提高。文献[24]使用Gabor变换系数构建了基于Gabor变换的特征,结果表明基于Gabor变换的特征比时域和谱域特征更为有效。直接提取信号变换的结果进行辐射源识别,存在大量的无效或冗余数据。无效数据对识别效果贡献不足,甚至会产生负面影响,冗余数据会增大计算量,影响辐射源识别效率。这些方法大多使用单一信号处理手段提取特征,难以全面准确地表示辐射源信号之间的细微差别,存在一定的局限性。

随着信号体制和电磁环境的复杂化,单一域的特征难以完整体现信号的特性,将这些特征进行融合,建立更高维度的特征向量集合,可以全面表达信号的特征,获得更优的识别效果。为解决现有分类方法[25-27]数据冗余和特征单一对分类效果的负面影响,本文综合现有方法与成果,提出一种多域特征融合(multi-domain feature fusion,MFF)的空间辐射源识别方法,通过对信号进行Hilbert-Huang变换和高阶谱分析,然后提取HHT边际谱和双谱的特征并将其拼接融合为信号的多域特征,采用SVM分类器进行分类识别,进行仿真实验,验证方法的性能。

2 辐射源细微特征识别

2.1 辐射源细微特征分析处理流程

通信设备细微特征提取与识别过程如图1所示,辐射源设备发送射频信号,通信接收机收到信号后,送入预处理机中,预处理的主要作用是对信号进行去噪处理,以削弱噪声的影响,加强有用信息;预处理后的数据将送入主处理机进行信号处理和特征提取,生成特征数据集送入分类识别模块;在分类识别模块,将已标注的特征数据集送入分类器中进行训练,再将待识别信号特征数据集送入训练后的分类器中,得到分类识别结果。

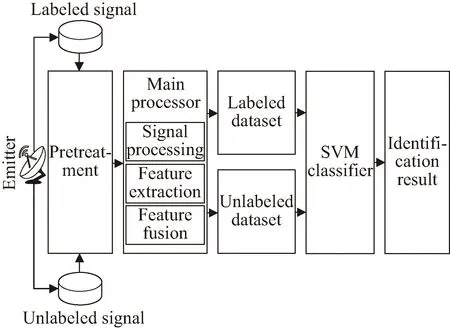
图1 通信设备细微特征提取与识别流程

2.2 功放模型及细微特征

功率放大器是通信发射机中的重要器件,为保证较高的工作效率,卫星转发器内部的高功率放大器通常工作在饱和状态或邻近饱和状态,导致输出的信号存在严重的非线性失真,是辐射源细微特征的主要来源。

一个双音复信号x(t)可以表示为:

式中:ai为信号的幅度;fi为信号的频率;θi为信号的相位。

假设功率放大器输入信号为x(t),输出信号y(t)可表示为:

式中:A[ai]为功率放大器由于非线性特性引起的幅度AM-AM失真;φ[ai]为相位AM-PM失真。卫星通信系统中,常采用行波管放大器作为转发器内部的高功率放大器。Saleh模型是针对行波管提出的失真模型[28],对幅度和相位失真均有描述:

图2给出了功率放大器的AM-AM、AM-PM特性曲线,体现了功率放大器的非线性特性。

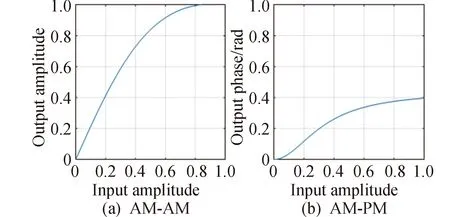
图2 功率放大器的AM-AM和AM-PM曲线

信号经过非线性功率放大器,会产生多种非线性产物,这些产物中蕴含着信号的细微特征。由功放产生的细微特征主要包含谐波、交调、互调、杂散等成分,影响信号的幅度、频率和相位。对于每一台辐射源设备,由于其内部的电子元件存在差异,导致信号的细微特性不同,从而形成辐射源个体识别的依据。

3 特征设计与分类识别方法

3.1 Hilbert-Huang变换

Hilbert-Huang变换利用经验模态分解(empirical mode decomposition,EMD)对原始信号进行处理,分解原始信号得到若干个本征模态函数(intrinsic mode function,IMF),再对得到的IMF进行Hilbert变换得到瞬时频率,从而获得信号的Hilbert时频谱[29]。

在经验模态分解过程中,信号s(t)被分解为IMF分量ci(t)与残留分量rn(t)之和,即:

图3为信号波形及其IMF分量,其中signal为原始信号s(t),之后依次为EMD分解之后得到IMF分量ci(t),分别称作IMF1～IMF6,最后为残留分量rn(t),每一个IMF分量代表了原始信号中存在的一种模态分量。IMF1频率最高,特征时间尺度最小。随着分解层数的增加,IMF分量的特征时间尺度增大,频率降低,多分量信号中的不同频率成分被分离出来。

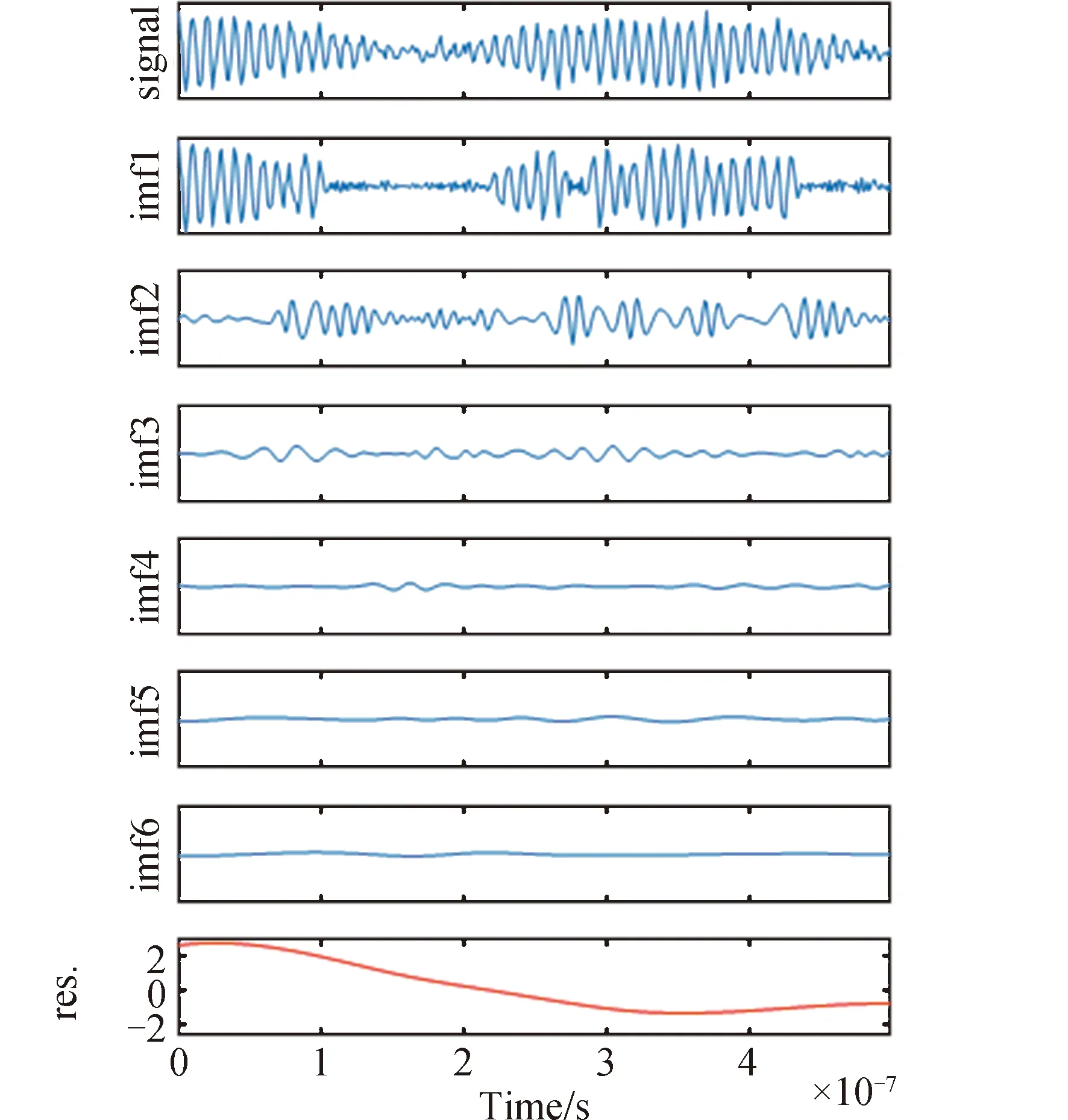
图3 信号及其IMF分量

EMD分解后的各个IMF分量经过Hilbert变换可以求得瞬时频率。原始信号可以表示为:

反映了信号幅值与时间、频率的关系,信号幅值可以表示为时间t和瞬时频率ω的函数H(ω,t),从而获得信号总的HHT时频谱:

图4所示为仿真信号的HHT时频谱图,由于EMD能够实现对信号成分的精细分析,H(ω,t)频率分辨率很高,信号的不同频率分量以及低频噪声分量清晰地显示出来,能较好反映信号的细微特征。

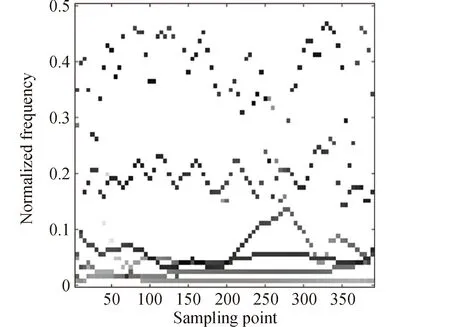
图4 信号的HHT时频谱

HHT边际谱由HHT时频谱沿时间轴进行积分得到:

图5为仿真信号的HHT边际谱图,是Hilbert时频谱在时间轴上的积分,它反映了每一个频率点上的幅值分布,代表信号的幅值在整个频率段上随频率变化的情况,反映了概率意义上幅值在整个数据跨度上的积累幅值。与傅里叶分析不同,傅里叶变换的频谱中某一频率处能量的存在代表该频率在整个时间轴上的存在,而HHT边际谱数值的大小表示该频率出现的概率高低,该频率出现的具体时刻由图 4中的HHT时频谱表示。

图5 信号的HHT边际谱

3.2 高阶谱分析

高阶谱是二维功率谱的推广,是高阶累积量的傅里叶变换,可以提供二阶统计量所没有的相位信息,适用于对信号细微特征的研究。

定义一个随机序列为:

{x(n),x(n+τ1),…,x(n+τk-1)}

其高阶累积量ckx(τ1,τ2,…,τk-1)满足:

则k阶谱是k阶累积量的k-1维离散时间傅里叶变换,即:

因此,三阶谱又称为双谱,四阶谱又称为三谱,分别定义如下:

双谱是阶数最低的高阶谱,在特征提取、故障检测方面有着较为广泛的应用,形成了较为成熟的理论和估计方法。图6是非线性信号在SNR=0dB条件下的双谱图。图7所示的双谱图是用等高线来定性刻画的,完整地保留了信号的双谱特征,最大限度地保留了信号原有的信息,方便观察不同辐射源信号高阶谱的差异。

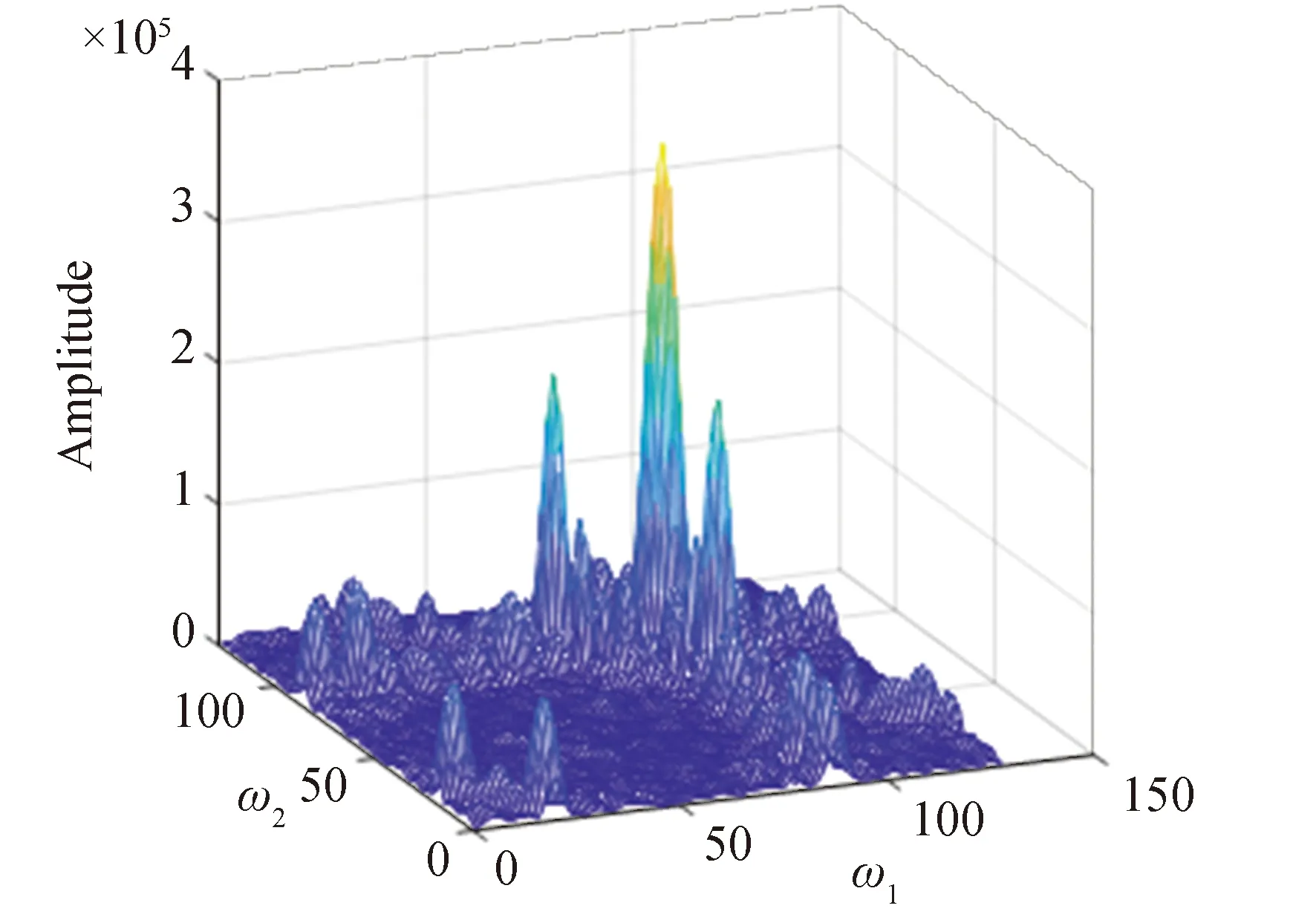
图6 信号的双谱

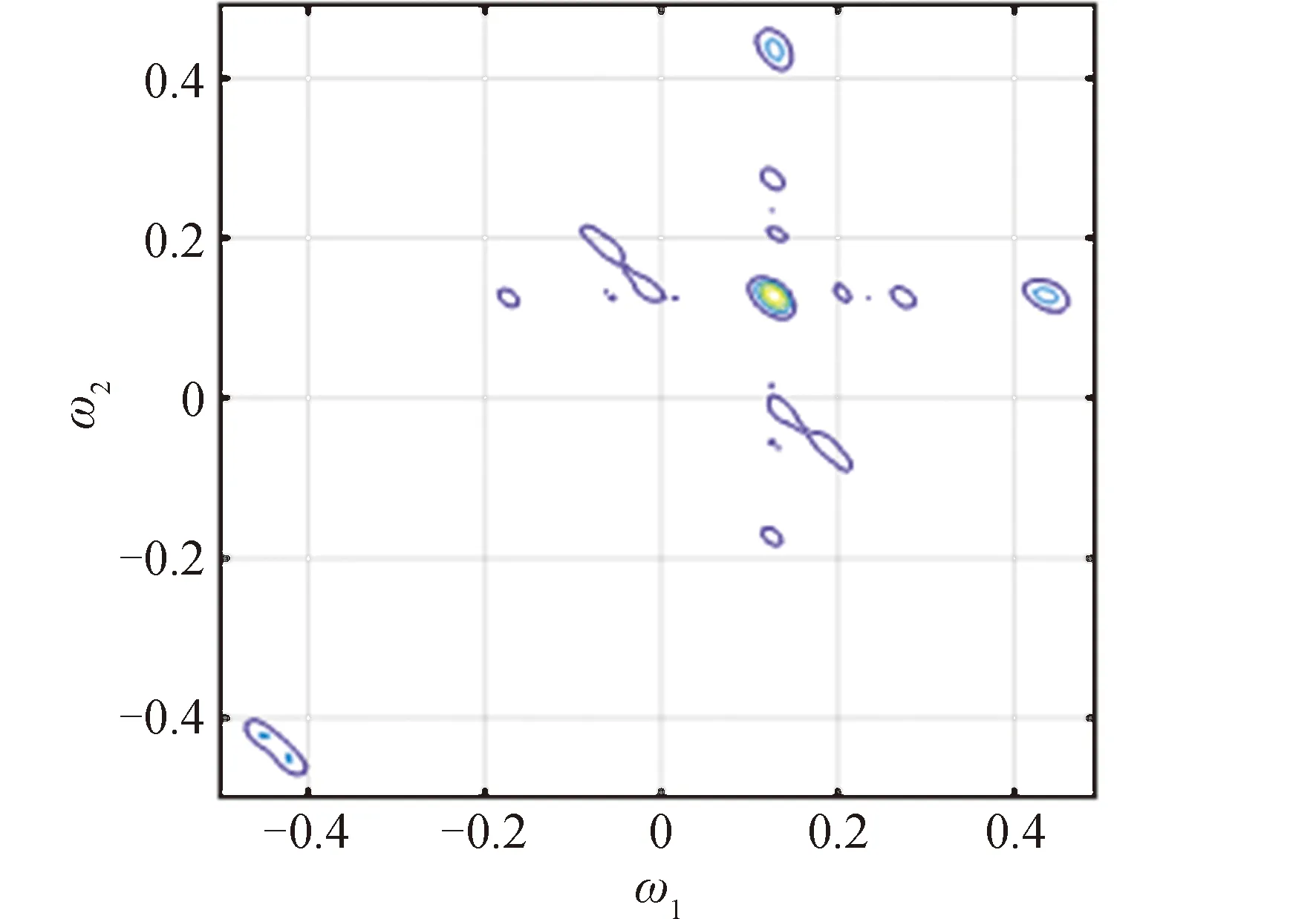
图7 通过FFT估计的双谱

3.3 MFF辐射源识别方法

单一域特征往往无法全面体现信号复杂丰富的特征信息,导致识别效果不佳。虽然单一域特征在分类识别中存在局限性,但将多种特征进行拼接融合,可以发挥特征在不同域的作用。多域融合特征设计的目的是尽量获得足够多的特征,构建新的多域特征向量空间,以更全面描述辐射源信号的细微特征,并通过多域特征表征不同信号的差异性,将辐射源识别的问题转换到高维特征空间中的判决区域划分,以实现更优的识别效果。

统计量是样本的函数,用于描述或者构建样本之间的关系,从样本数据中提取信息并推断总体信息。信息熵可以表征样本数据能量的分布情况。有效的辐射源细微特征应当具有较强的判别性以及较低的冗余性。根据上述原则,本文设计了辐射源多域特征集合,如图8所示。

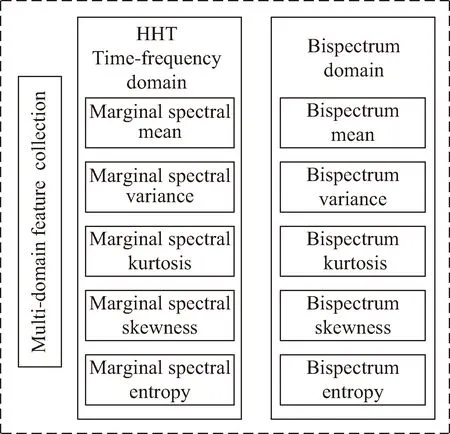
图8 辐射源多域特征集合

对于一个随机变量X,数学期望为D(X)。其方差定义为:

D(X)=E{[X-E(X)]2}

峰度定义为:

偏度定义为:

使用EMD算法分解信号,并进行Hilbert变换,求得HHT边际谱J(ω)。基于HHT边际谱的特征设计包括以下统计特征。

1)HHT边际谱均值AVGJ为:

AVGJ=E[J(ω)]

2)HHT边际谱方差VARJ为:

VARJ=D[J(ω)]

3)HHT边际谱信息熵HseJ为:

4)HHT边际谱峰度KurtJ为:

KurtJ=Kurt[J(ω)]

5)HHT边际谱偏度SkewJ为:

SkewJ=Skew[J(ω)]

定义双谱矩阵为:

双谱投影为:

基于双谱的特征设计包括以下统计特征。

1)双谱均值AVGB为:

AVGB=E[Bx(ω1,ω2)]

2)双谱方差VARJ为:

VARB=D[Bx(ω1,ω2)]

3)双谱信息熵HseB为:

4)双谱投影峰度KurtP为:

KurtP=Kurt(P)

5)双谱投影偏度SkewP为:

SkewP=Skew(P)

在特征融合的基础上,本文设计了基于MFF的辐射源识别方法,流程如图9所示。原始信号集合包含已标注信号和未知信号,将其送入非线性元件并加以高斯白噪声,得到有噪声的失真信号集合;对失真信号集合分别进行Hilbert-Huang变换和高阶谱分析,得到信号的HHT边际谱和双谱;然后进行特征提取和特征融合,提取HHT边际谱的均值、方差、峰度、偏度和信息熵作为信号HHT时频域特征,提取双谱均值、双谱方差、双谱投影峰度、双谱投影偏度和双谱信息熵作为信号的双谱域特征,再将其拼接融合得到多域特征集合;最后将已标注的多域特征送入SVM分类器中进行训练,将待识别的多域特征送入训练好的分类器中,得到分类识别结果。

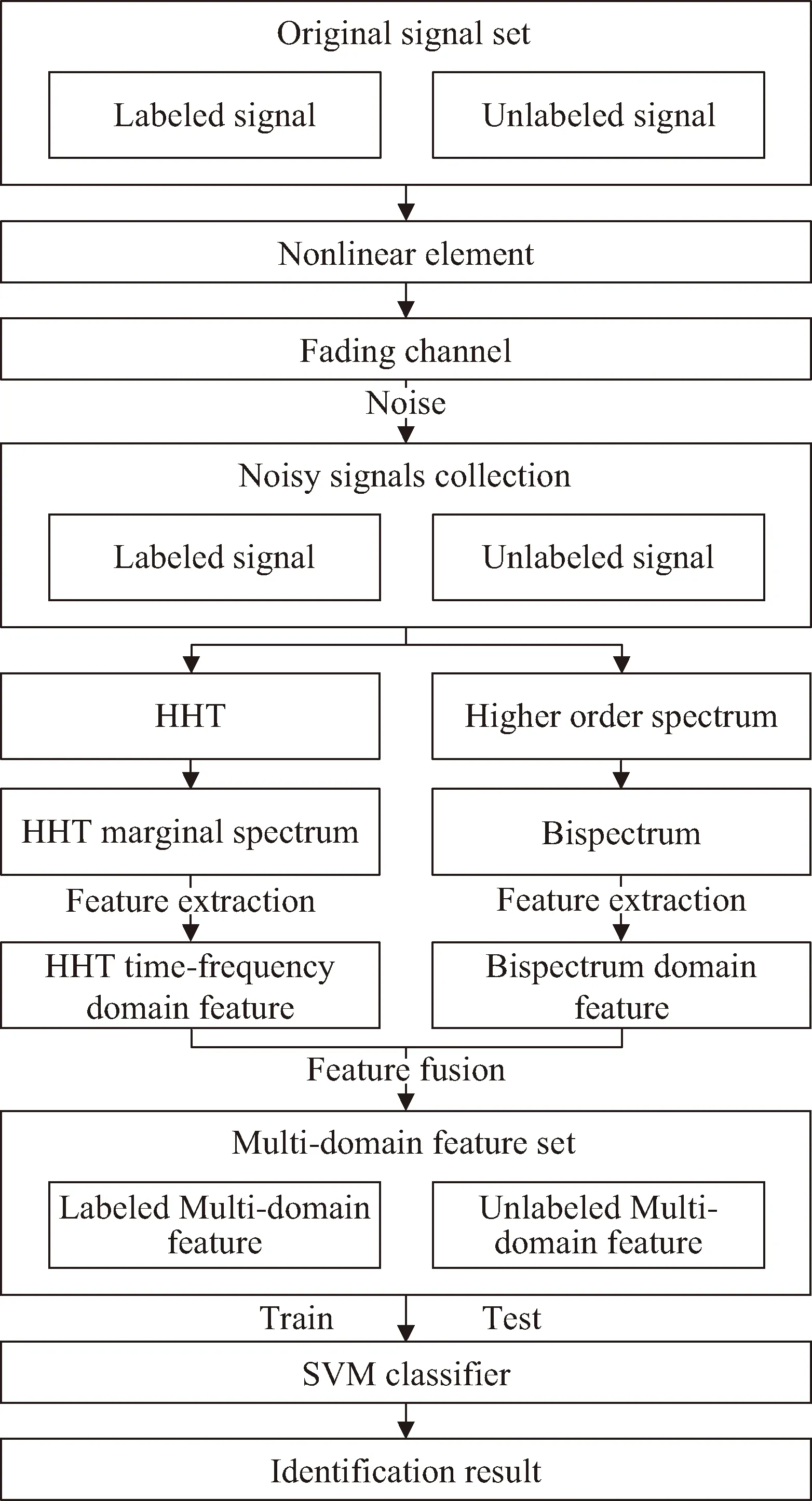
图9 基于MFF的辐射源识别方法流程

4 试验设置与结果分析

4.1 试验设置

为了评价多域融合的辐射源识别方法,本次仿真试验对发射端的非线性失真进行了仿真,功率放大器采用Saleh模型,模拟了信号的谐波、交调、互调、杂散等非线性产物特征,将本文提出的方法与传统基于HHT边际谱、边际谱信息熵、双谱投影、双谱矩形积分、四阶累积量切片谱的分类识别方法进行了比较。

实际的通信卫星工作在L、C、S、Ku及Ka频段,在试验设置中,使用不失代表性的简单模型,参考Inmarsat和Thuraya卫星通信系统,卫星转发器带宽36MHz,共划分为120个子带,多路转发器相邻通道的频率间隔为300kHz,10MHz、10.3MHz对应原始信号的两个射频频点,发送到卫星转发器的两个通道中,然后经过变频、放大到下行1626MHz、1626.3MHz两个频点,在卫星地面站接收到高频信号,将其下变频至10MHz、10.3MHz的中频频段,在中频接收机选取80MHz的频率对信号进行采样,选取每段信号的长度为N=400。设置辐射源个数为4个,辐射源输入相同的信号并加以高斯白噪声,信噪比的设置SNR∈[0,20]dB,其中,SNR仿真步长为1dB。在仿真信号中,每个信噪比下选取50段构成有标签的训练数据集,并在同样的信噪比设置下分别选取50段构成测试数据集。

然后进行预处理,对训练集和测试集信号进行小波阈值去噪,对小波系数进行阈值处理。因为小波变换后有用信号的能量主要集中在少数绝对值较大的小波系数上和特定的频率范围内,而噪声的能量却分布于整个小波域内。小波分解后的有用信号的系数幅值会大于噪声的系数幅值,采用阈值处理的方法可实现信号去噪。

4.2 试验结果分析

为验证试验结果的有效性,进行如下试验,将本文提出的多域融合识别方法与传统方法进行对比,将训练集输入到SVM分类器中,训练不同的分类器,将测试集输入分类器中进行分类,计算正确率,表1为各种方法分类器的输入。边际谱信息熵描述信号边际谱的不确定性;四阶累积量切片谱是四阶谱在一维的投影;双谱投影和双谱矩形路径积分通过不同的积分路径将二维双谱通过积分转化为一维数据进行处理;传统方法常把上述特征作为衡量信号细微特征的重要参数。

表1 试验设置

SVM算法最初是为二值分类问题设计的,当处理多类问题时,就需要构造合适的多类分类器。本文采用一对一 SVM,在任意两类样本之间设计一个SVM分类器,k个类别的样本就需要设计k(k-1)/2个SVM分类器。当对测试数据进行分类时,对所有的分类器分别进行测试,并保存结果,最后得票最多的类别即为该样本的类别。

对去噪后的信号进行HHT变换,得到信号的HHT边际谱,图10是在SNR=20dB下4台发射机信号的HHT边际谱。

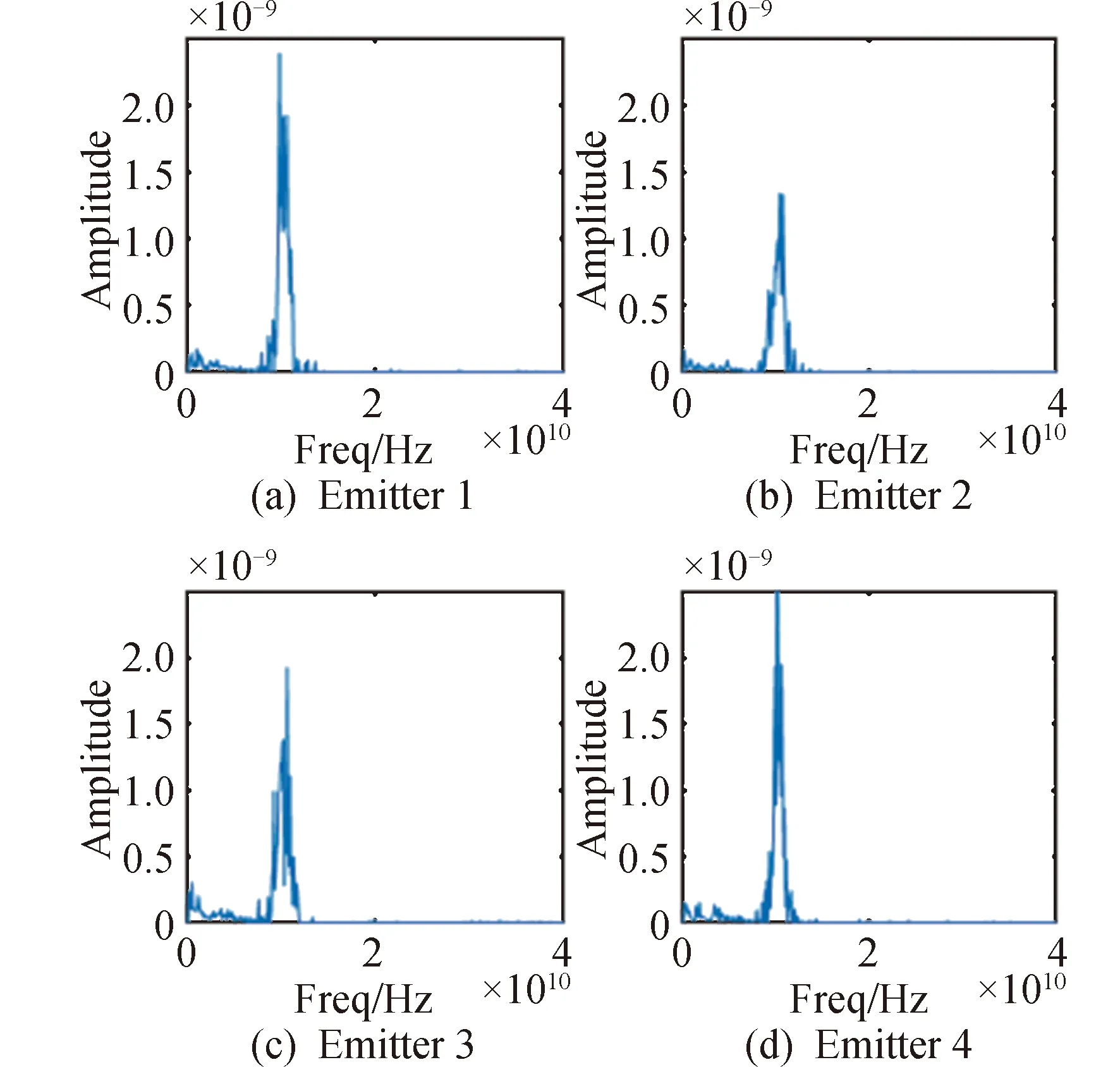
图10 SNR=20dB信号的HHT边际谱

提取HHT边谱的均值、方差、峰度、偏度、信息熵特征,为方便显示,固定三维图像的X轴代表HHT边际谱的均值,Y轴代表方差,Z轴分别代表HHT边际谱的偏度、峰度和信息熵,绘制特征空间分布散点图,如图11～13所示。

图11 HHT边谱均值-方差-偏度

图12 HHT边谱均值-方差-峰度

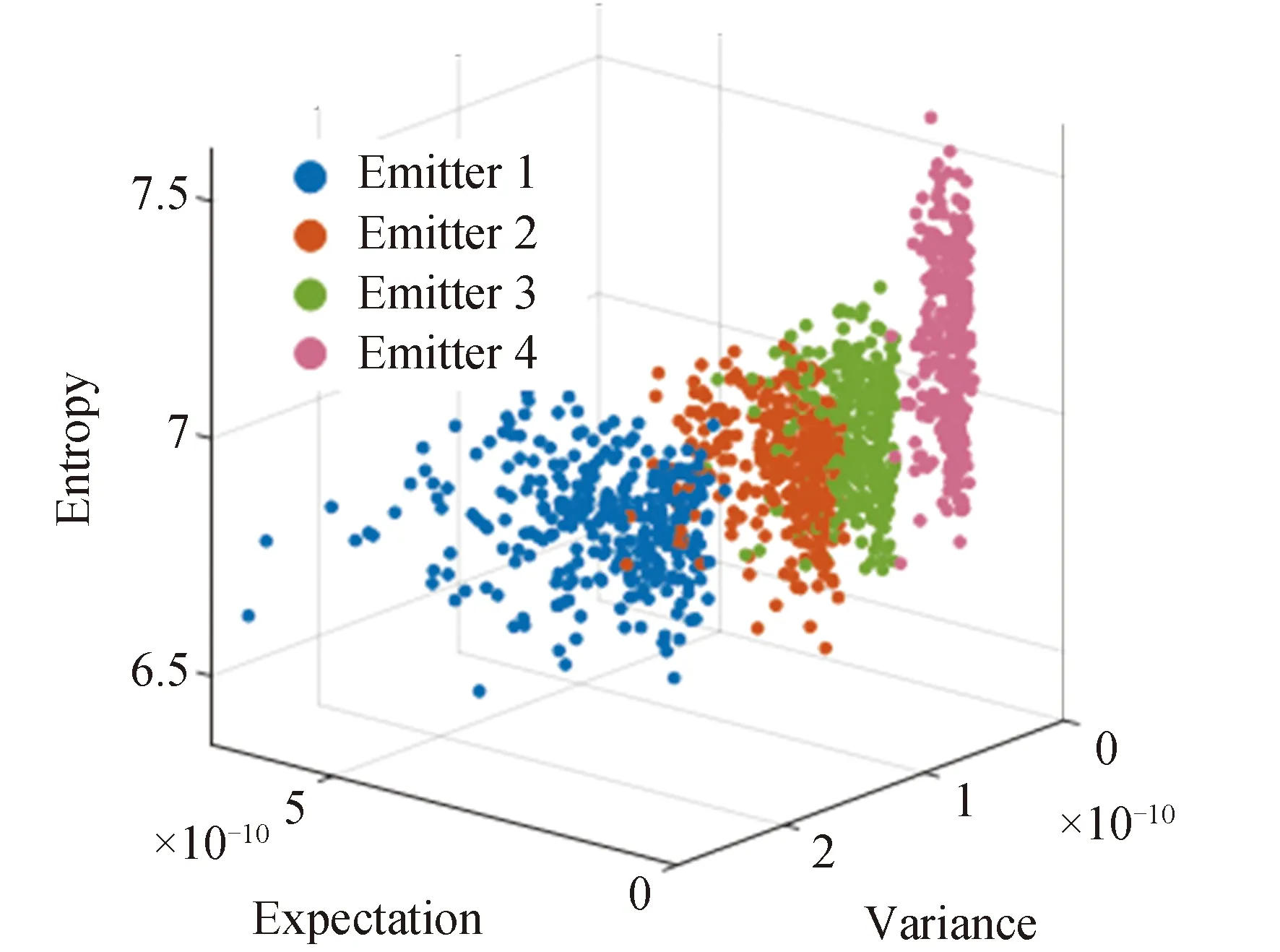
图13 HHT边谱均值-方差-熵

然后计算信号的双谱,图14为SNR=20dB下4台发射机信号的双谱图像。

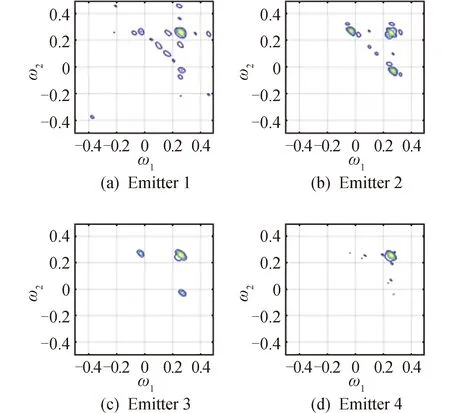
图14 SNR=20dB 信号的双谱图像

提取双谱均值、双谱方差、双谱投影峰度、双谱投影偏度和双谱熵,为方便显示,固定三维图像的X轴代表双谱的均值,Y轴代表双谱方差,Z轴分别代表双谱投影峰度、双谱投影偏度和双谱熵,绘制特征空间分布散点图,如图15～17所示。

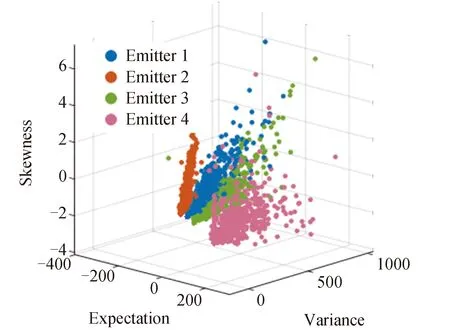
图15 双谱均值-方差-偏度

图16 双谱均值-方差-峰度

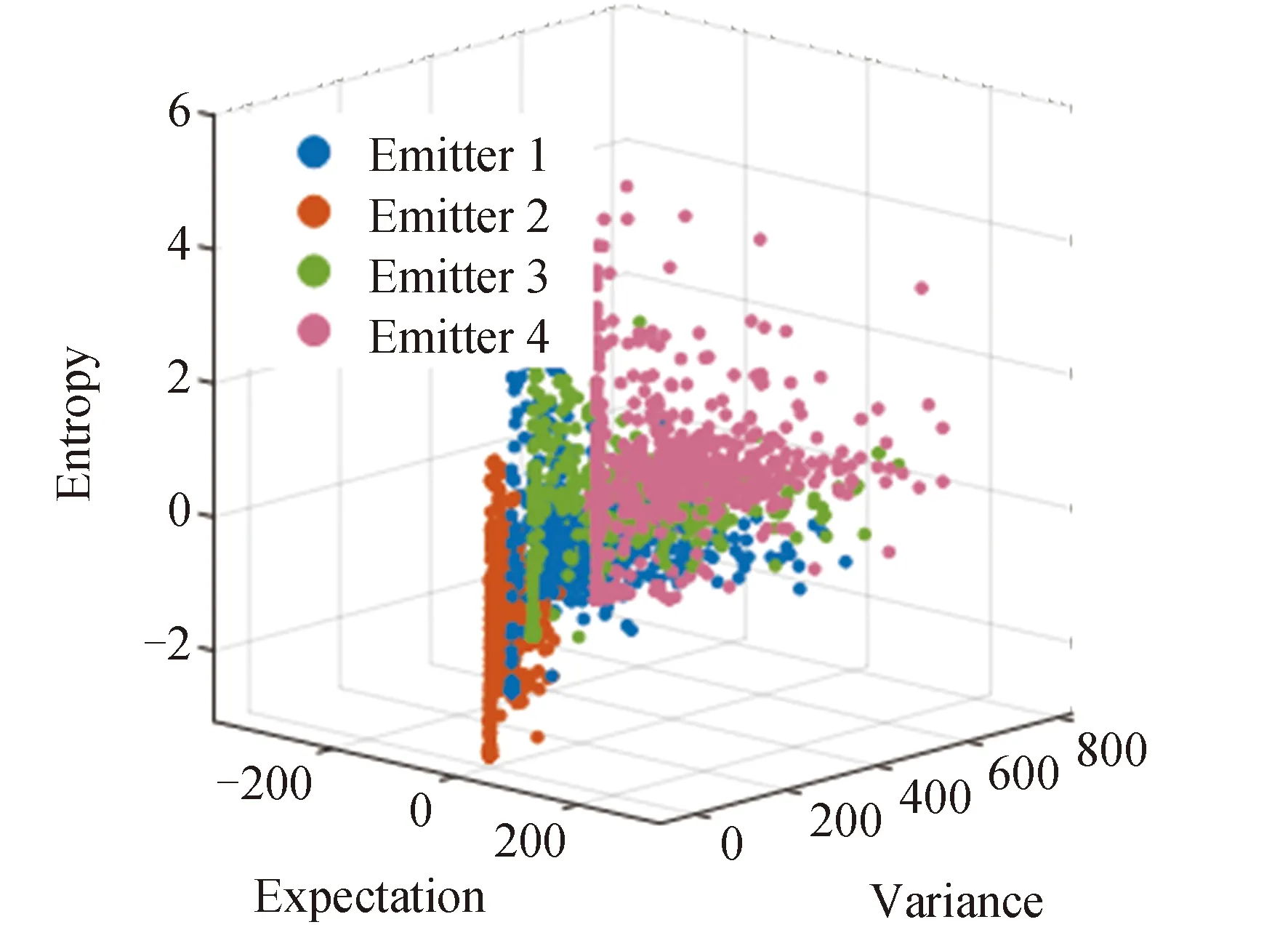
图17 双谱均值-方差-熵

可以看出,不同发射机信号的HHT边际谱和双谱图像具有细微差异,这些细微区别是辐射源发射机硬件的不同引起的,是发射机固有特性在信号上的体现。因此HHT边际谱和双谱可以用于提取个体信号的特征,满足辐射源个体识别的基本要求。

在HHT边际谱和双谱的特征分布散点图中,以不同颜色表示不同辐射源个体的特征。除个别异常值外,特征总体呈现明显的同类聚集性和类间分离性,具有良好区分度,能够反映不同的辐射源个体的差异。

图18为4台发射机的四阶累积量切片谱。四阶累积量是一个有3个参数变量的四维函数,三谱即四阶谱,是四阶累积量的三维离散时间傅里叶变换,但计算量大且耗时长,在有限数据情况下相对于相关运算其估计方差较大。四阶累积量切片谱实质上是四阶谱在一维的投影,四阶累积量切片谱比四阶谱明显简化了计算的复杂度,但保留了其抑制高斯噪声的固有优点,利于实际应用中的图形显示。

图18 四阶累积量切片谱

对基于HHT边际谱、边际谱信息熵、双谱投影、双谱矩形积分、四阶累积量切片谱的分类识别方法及本节所提方法的分类结果进行对比分析,具体的分类结果随SNR的变化特性曲线如图19所示。

图19 不同方法分类效果曲线

由图 19可得,对比基于HHT边际谱、边际谱信息熵、双谱投影、双谱矩形积分、四阶累积量切片谱的分类识别方法,本文提出的MFF方法有着更好的性能。MFF方法自SNR=9dB开始,分类正确率开始显著提高,自SNR=13dB开始,分类正确率的升高趋于平缓,SNR≥16dB时,可以达到90%以上的分类正确率。在SNR=20dB时,基于HHT边际谱方法的分类正确率为65.45%,基于边际谱信息熵方法的分类正确率为86.03%,基于双谱投影方法的分类正确率为79.98%,基于双谱矩形路径积分方法的分类正确率为70.15%,基于四阶累积量切片谱方法的分类正确率为83.77%,本文方法的正确率达到95.44%,同对比组中效果最好的基于边际谱信息熵方法相比,正确率有9.41%的提升。

从分类效果曲线图中可看出,分类正确率主要受到特征提取和信噪比高低的影响。特征是决定辐射源个体识别效果的关键,特征提取的目的就是寻找表征显著类别差异的信息,提取出最能表征原始数据本质信息的少量综合特征。直接提取信号变换的结果进行辐射源识别,存在大量的无效或冗余数据,并且单一域的特征难以完整体现信号的特性,这些都对辐射源识别带来困难。辐射源的特征十分细微,容易淹没在噪声中。噪声对识别正确率有着很大影响,不同方法的分类正确率都随着信噪比的增大而提高,在10dB信噪比附近,各方法的正确率开始显著提高。