基于常应变单元的空间薄膜结构动力学建模与分析

2023-09-18杜雪林张康张瑞翔叶拓易文慧蒋嘉斌

中国空间科学技术 2023年4期

杜雪林,张康,张瑞翔,叶拓,易文慧,蒋嘉斌

1.湖南工学院智能制造与机械工程学院,衡阳 421002

2.西安电子科技大学电子装备结构设计教育部重点实验室,西安 710071

1 引言

目前,载人航天、深空探测、大型空间望远镜和对地观测等航天任务的开展和推进,无不对空间薄膜结构的应用提出了迫切要求。空间薄膜结构质量轻、易折叠,可被应用在静电成形薄膜反射面天线、充气式可展开天线及太阳帆等航天器中,可作为新型空间展开结构解决空间结构日益增大及运载火箭体积有限之间的矛盾[1-4]。为了提高星载天线的在轨性能和可靠性,需要进一步系统开展采用大型可展开天线的动力学研究[5]。

空间膜结构是由高强度膜材料通过一定方式施加预张力从而形成特定空间形状并能承担相应外部载荷的一种结构[6]。对薄膜结构的动力学分析方面,往往采用大量的薄壳、索和膜等大变形和强几何非线性单元,因此在展开过程中会发生大变形和大转动,具有强非线性、复杂接触等特点,动力学建模与分析难度较大[7]。近年来,不少研究者对大型薄膜天线的动力学建模进行了研究。如,Shen等[8]利用ABAQUS分析了张拉索提供的预张载荷发生变化时膜天线的模态振型和固有频率[8]。Fan等研究了大型膜天线卫星系统的动力学建模和在轨参数辨识问题,利用耦合系数法建立了卫星系统的平动、转动和振动动力学方程[9]。Yuan等研究了可折叠折纸空间膜结构展开过程中考虑接触冲击的动力学建模问题[10]。余建新等建立了充气展开反射面的有限元模型,采用气囊模型和控制气体法分析反射面从缠绕状态到完全展开状态的全过程[11]。王永等针对太阳帆航天器的薄膜帆面和大尺度杆的柔性特征,建立了相应的非线性刚柔耦合动力学模型,并研究了对应的控制方法[12]。荣吉利等采用有限元数值分析的方法,在 NASA 模态分析数值模型的基础上,建立了圆形薄膜太阳翼展开动力学模型,以不同的展开控制函数为变量,研究了不同控制函数对展开平稳性的影响[13]。Lampani等采用非线性有限元法对三维充气结构的展开机理进行分析,指出当问题的几何变化不极端时,隐式有限元解可以提供更多的结果,而显式方法能够求解更复杂的充气系统的时间解[14]。肖潇等采用弹簧-质点模型,对充气管的充气展开过程进行数值模拟,得到在无重力环境下不同时刻卷曲折叠管的展开构型[15]。Xu等对整个天线结构进行了参数化建模和分析,采用罚函数法求解薄膜的自接触,基于改进的弹簧-质量系统对天线展开机构进行了仿真[16]。Borse等通过在MATLAB中进行有限元应力分析,对方形、扁平、薄充气膜结构的性能进行预测[17]。Li等建立了包含索单元、膜单元和梁单元的集成有限元模型,对钢支撑结构的张拉膜进行分析[18]。Liu等建立了具有参数不确定性的阻尼膜结构动力分析的随机动力刚度解析公式,所开发的随机动力刚度单元可以在考虑不确定性的一般边界条件下组装成膜组件的模型[19]。Liu等提出了一种将褶皱/松弛模型集成到柔性多体动力学绝对节点坐标系薄壳单元中的计算方法,研究展开太阳帆和充气气囊等膜系统动力学分析中的褶皱现象[20]。总的来看,目前空间薄膜结构的研究主要采用增量有限元方法,由于膜结构的大位移和大变形,接触等因素的,往往导致刚度矩阵奇异,造成求解困难。

本文由有限元离散方法将整个薄膜反射面离散为众多三角形单元,这些单元的节点可视作质点,考虑这些三角形单元的弹性势能,由最小势能原理得到三角形单元的平衡方程,从而得到了薄膜反射面的有限元分析模型,进一步建立单元间的接触模型,开展空间薄膜系统的展开动力学分析。基于薄板的下落算例,验证了方法的正确性,随后,在重力环境下,对薄膜反射面天线进行动力学展开分析,经过该展开动力学分析算例,对薄膜反射面展开过程的平稳性和动力学参数进行分析预测。

2 常应变三角形膜单元

空间薄膜结构往往构成抛物面反射面以满足空间任务的需求,针对该类光滑连续的空间曲面,常基于有限单元法对目标曲面的变形予以建模。由有限元离散方法将整个薄膜反射面离散为众多三角形单元,并建立对应拓扑关系的薄膜反射面数值分析模型,基于有限元建立了薄膜结构的展开动力学分析模型。为此,本节先建立用于离散空间薄膜结构的三角形单元,并给出该单元上点的应变和单元三条斜边线应变之间的转换关系。杜敬利等[21]提出三角形薄膜单元在不受力状态时,可由其边长描述膜单元的几何构型。当三角形膜单元在不受力状态下时,膜单元的几何构型如图1所示,该膜单元杨氏模量记作Em,薄膜厚度记作tm,泊松比记作vm。在三角形膜单元中,边12、边23及边13所对应初始长度为l1、l2和l3。设定三角形膜单元的位移场为线性,由于应变为位移场的一阶导数,故应变为常数,即为常应变三角形单元。当膜单元受力变形后,三角形膜单元的节点1、节点2和节点3对应坐标矢量则记为x1、x2和x3。膜单元受力拉伸后,沿边12、边23和边13的应变如下:

(1)

应变的微分为:

(2)

在图1中,选择三角形膜单元节点1为坐标系原点,将边12方向看作x轴,取坐标系平面和平面123重合,即得到局部坐标系Omxmym。在局部坐标系中,任意位于该三角形上的点的应变表示:

ε=[εxεyγxy]T

(3)

式中:εx和εy沿xm和ym方向的正应变记作εx和εy,切应变记为γxy。

现将xm轴由当前位置逆时针转动,旋转角度为α0,沿该方向的正应变记为εp,基于公式(3),可得到εp的表达式:

εp=cos2α0εx+sin2α0εy+cosα0sinα0γxy

(4)

由公式(4),进一步可联系公式(1)和(3),得到:

εl=Ttε

(5)

式中:

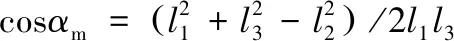
三角形膜单元上的弹性势能和外力做功之和为:

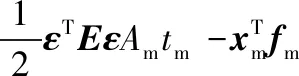
(6)

Am=[p(p-l1)(p-l2)(p-l3)]1/2

(7)

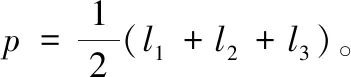
基于式(1)、(2)和(5),势能的微分为:

(8)

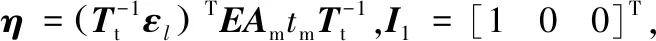
上式可另写作:

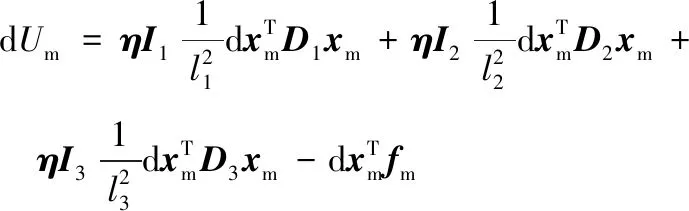
(9)

因此,基于最小势能原理,得到了三角形单元的平衡方程为:

km(lm,xm)xm-fm=0

(10)

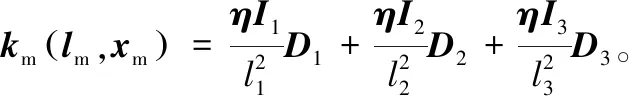
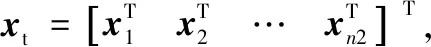
K(lt,xt)xt=F

(11)

式中:F为节点上的力向量可经由外荷载P转换得到,K(lt,xt)是关于节点位置矢量xt和单元边长lt的总体刚度矩阵。

所建立平面常应变三角形单元模型由三个节点坐标确定,单元上材料点的位置和变形是在全局坐标下定义的,简化了几何描述和坐标转换,能够满足非线性收敛准则。

3 单元间的接触模型

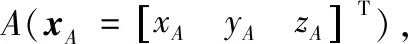
现任取薄膜反射面上的某单元123和对应膜单元的任意节点A,如图2所示,可知单元123上的边21、31和32的方向矢量写为:

图2 薄膜接触判断

n21=x2-x1,n31=x3-x1,n32=x3-x2

(12)

该薄膜单元所在平面的法向矢量可记作:

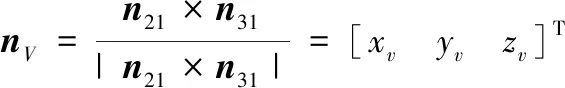
(13)

其中nV为该平面的法向单位矢量。

进一步可得到平面的方程:

nV(x-xi)=0,i=∀(1,2,3)

(14)

式中:x为单元上任意点的坐标矢量。

现需要判断点A相对于平面的位置,有nV·(xA-xi)>0,i=∀(1,2,3)时质点A位于平面123的上方,否则,则处于平面123的下方,如图2所示,质点A此时位于平面的上方。

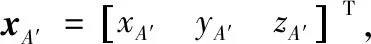
(15)

可通过对投影点A′和三角形节点1、2和3分别形成的三角形A′12、A′13和A′23面积和来判别A′是否位于三角形单元上。即,如SΔA′12+SΔA′13+SΔA′23=SΔ123时,投影点处在三角形单元区域内,反之,投影点A′处于三角形单元区域外。

因此,可知如果投影点A′位于三角形单元123上,则点A和三角形单元123构成接触对,存在接触的可能性。此时,需要确保点A和单元123之间的距离不得小于给定的距离,否则就需要施加惩罚力,避免接触的发生。

在此,给定惩罚力Fp,如果点A位于三角形单元123平面的上方时:

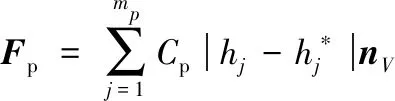
(16)

而当质点A处于单元123平面的下方时:

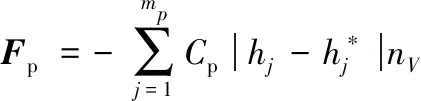
(17)

且:

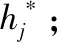
4 薄膜结构展开动力学方程

空间薄膜结构可被离散为众多的三角形单元,可将这些三角形单元的节点看作对应质点,对应质点上的质量与其所处于的三角形的形状和数目相关,由三角形的面积求质点的质量,即:

(18)

式中:ρM为膜材料的密度;Ak为连接质点i的第k个三角形单元的面积;s为连接质点i的所有三角形单元数量;αi,k为以质点i做顶点的第k个三角形单元的内角。

从而可知,整个空间薄膜反射面可经离散为众多的三角形单元,把得到的节点看作质点,根据对应的单元间拓扑关系,组集整个薄膜反射面的质量矩阵和刚度矩阵,得到最终的展开动力学方程:

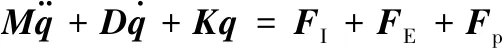
(19)

式中:M、D和K分别为薄膜反射面的总体质量矩阵、比例阻尼矩阵和总体刚度矩阵;FI为节点上的惯性力;FE为系统所受外力矢量;Fp为系统界面需引入的惩罚力。

采用Rayleigh比例阻尼矩阵[22],则D可写为:

D=β1M+β2K

(20)

式中:β1和β2为比例系数。

5 算例分析

5.1 薄板单摆动力学仿真

由动力学模型式(20),先建立重力环境下的空间薄板单摆模型,进行算例分析,此处薄板参数同文献[23],空间薄板的几何参数如图3(a)所示,板材料弹性模量取0.1MPa,材料密度为7810kg/m3,板材厚度为0.01m,泊松比取0.3。在薄板A点有一固定球铰,在重力的作用下薄板做单摆运动。采用三角形单元对薄板进行网格划分,并标示了一些关键节点,在图3(b)中,网格模型中,共划分三角形单元200个,节点数目121。设定单摆时间为0.3s,进行动力学仿真分析。

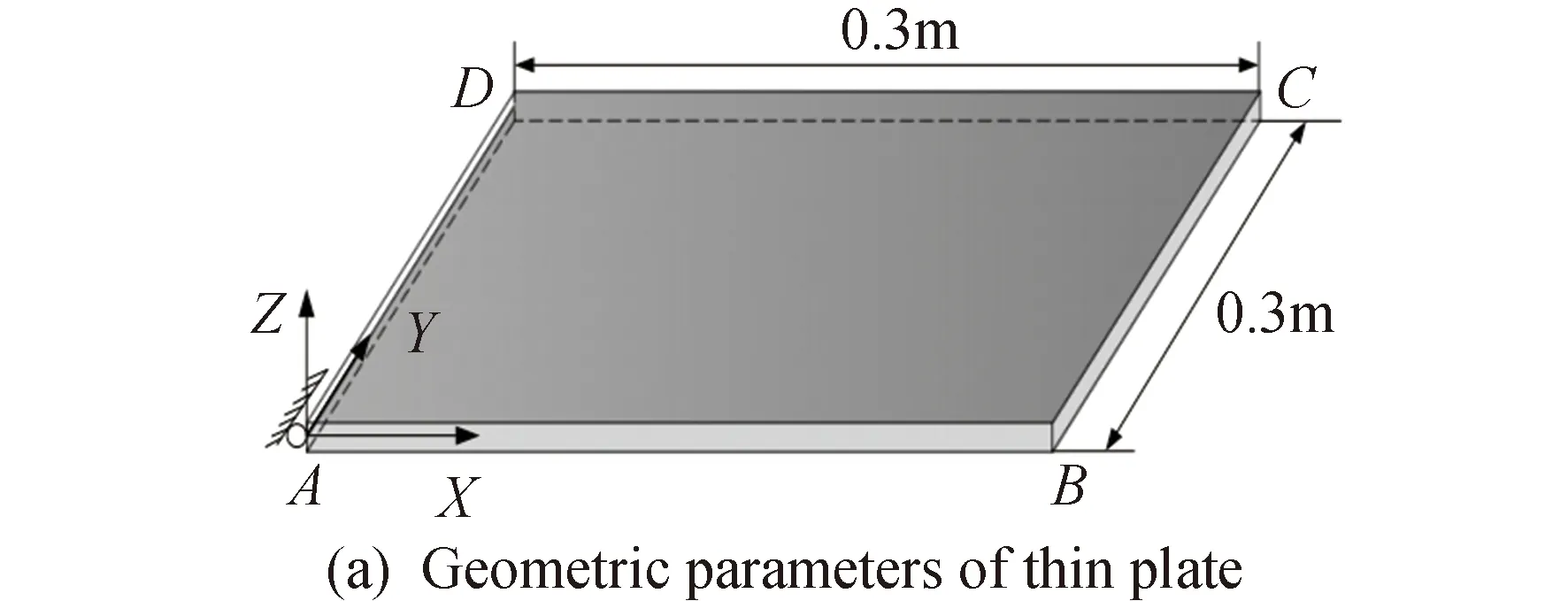
图3 薄板模型和网格分布

经过计算得到如下结果,不同时间对应的薄板构型如图4(a)所示,结果同文献[23]基本一致。各关键点的位移曲线,即这些节点沿x、y和z轴的位移曲线分别示于图4(b-d)。

图4 下落中的薄板构型和关键节点的位移曲线

由图可见,处于同边的节点的位移在下落前期运动状态一致,如P4和P7、P2和P3等,位置对称的节点如P4和P2、P7和P3、P6和P8等其位移变化也具有对称性(如P4、P7和P8沿x方向的位移曲线分别同P2、P3和P6沿y方向的位移曲线一致,反之亦然)。从结果上看,本仿真分析算例得到的结果合理且准确。

5.2 径向肋薄膜伞状天线的展开动力学分析

径向肋薄膜伞状天线具有较为简单的结构形式,但是可靠性强并且展开后表面精度高,展开机制和雨伞类似,因此应用广泛。径向肋薄膜伞状天线主要有径向肋和薄膜反射面构成,在径向肋之间连接有剪裁的扇形薄膜反射面,从而形成整个抛物反射面。伞状天线的收展运动是由径向肋的运动带动薄膜反射面实现的,在此,给出了共6个刚性肋的径向肋薄膜伞状天线的简化模型,如图5所示,随后对天线的展开过程进行动力学分析。

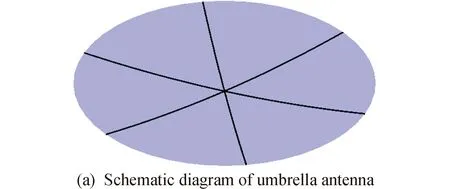
图5 简化的伞状天线反射面

将高强度的径向肋看作刚体,先结合径向肋的几何性质作运动学分析,任意取一根刚性肋,如图6所示。将选定的刚性肋离散为n-1个单元,共n个节点,在刚性肋的收展运动中,各个节点的位移可经由几何关系进行推导。

图6 刚性肋的运动学分析

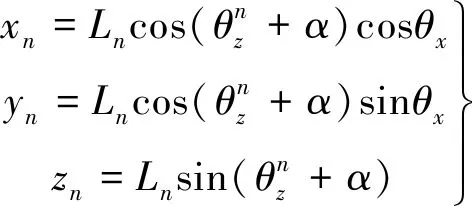
(21)

节点n的速度矢量:

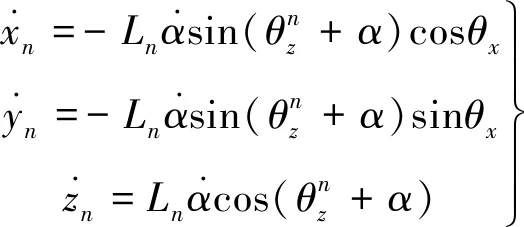
(22)

节点n的加速度矢量

(23)

对刚性肋进行运动学分析,设定图5中的天线孔径为0.55m,抛物面焦距1.1m,展开时间设定为1s,展开角度α=60°,对角速度进行规划,规划曲线见图7。在t=0s时天线处于收拢状态,而t=1s时天线完全展开。

图7 展开角速度规划

综合考虑刚性肋和薄膜反射面,建立径向肋薄膜伞状天线整体动力学模型。薄膜反射面的物理参数,如表1所示,膜材料的密度为1390kg/m3,膜的现时构型内预应变状态为膜内各点沿径向应变1.338×10-4,纬向应变1.338×10-4,阻尼系数β1和β2分别取0.5 和0.001。刚性肋的运动带动薄膜反射面收展,由于柔性薄膜构型未知,在此,先由完全展开态构型逆向收拢得到伞状天线的收拢态构型,再逐渐由收拢态进行展开分析。因此,把整个薄膜反射面离散为1200个三角形单元,共计661个节点,网格划分模型图如图8(a),该模型为轴对称模型,因此可取1/6模型上三个关键节点跟踪位移和速度,关键节点的位置和编号如图8(b)。在展开过程中,由于反射面的中心和刚性肋中心铰处固连,为此,需要施加对应的位移约束:

表1 反射面的物理参数

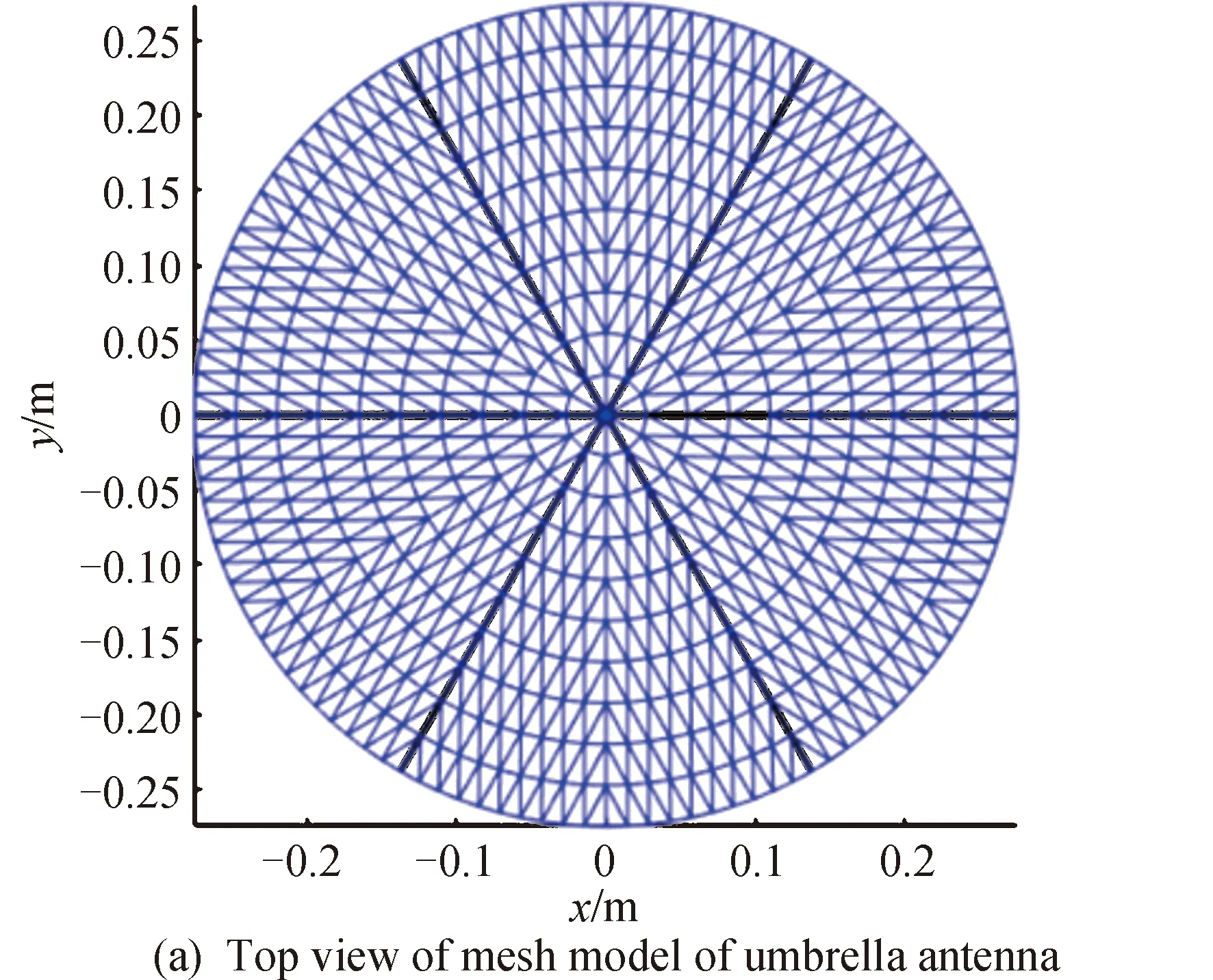
图8 伞状天线薄膜反射面网格模型

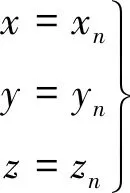
(24)

展开过程中伞状天线的构型图如图9,由图中可以观察到展开过程中反射面的构型变化。取展开时间为t=0.1s、t=0.3s、t=0.7s和t=0.9s,提取对应时刻的薄膜反射面的位移,绘制位移云图,如图10所示,进一步可明确展开过程中薄膜反射面的变形情况。由图可知,整个展开过程,薄膜上节点都表现出良好的对称性,节点位移由外径向内径呈逐渐减小趋势,最大节点位移发生在刚性肋顶点处,同实际情况一致。

图10 薄膜反射面的位移云图

为了清晰表征展开性能,求解并绘制了整个过程的薄膜反射面动能和应变能变化曲线,如图11所示,由图11(a)观之,0～0.4s 区间反射面上节点速度变化幅度大,然后渐趋平稳,后期刚性肋展至设计位置后,动能渐趋于零。总体来看,动能曲线存在局部震荡,也说明了膜本身具有的柔性特征。需要指出,类似存在大变形膜结构的动力学展开模拟中,往往需要将步长设置的足够小来保证数值收敛。由图11(b)观之,约在0～0.8s区间,应变能曲线整体平稳但存在振荡,这期间肋间薄膜未被完全张紧,在0.8-1s区间,整个薄膜反射面在刚性肋的张紧作用下,逐渐完全展开,对应地观察到应变能曲线在该区间呈上升趋势。

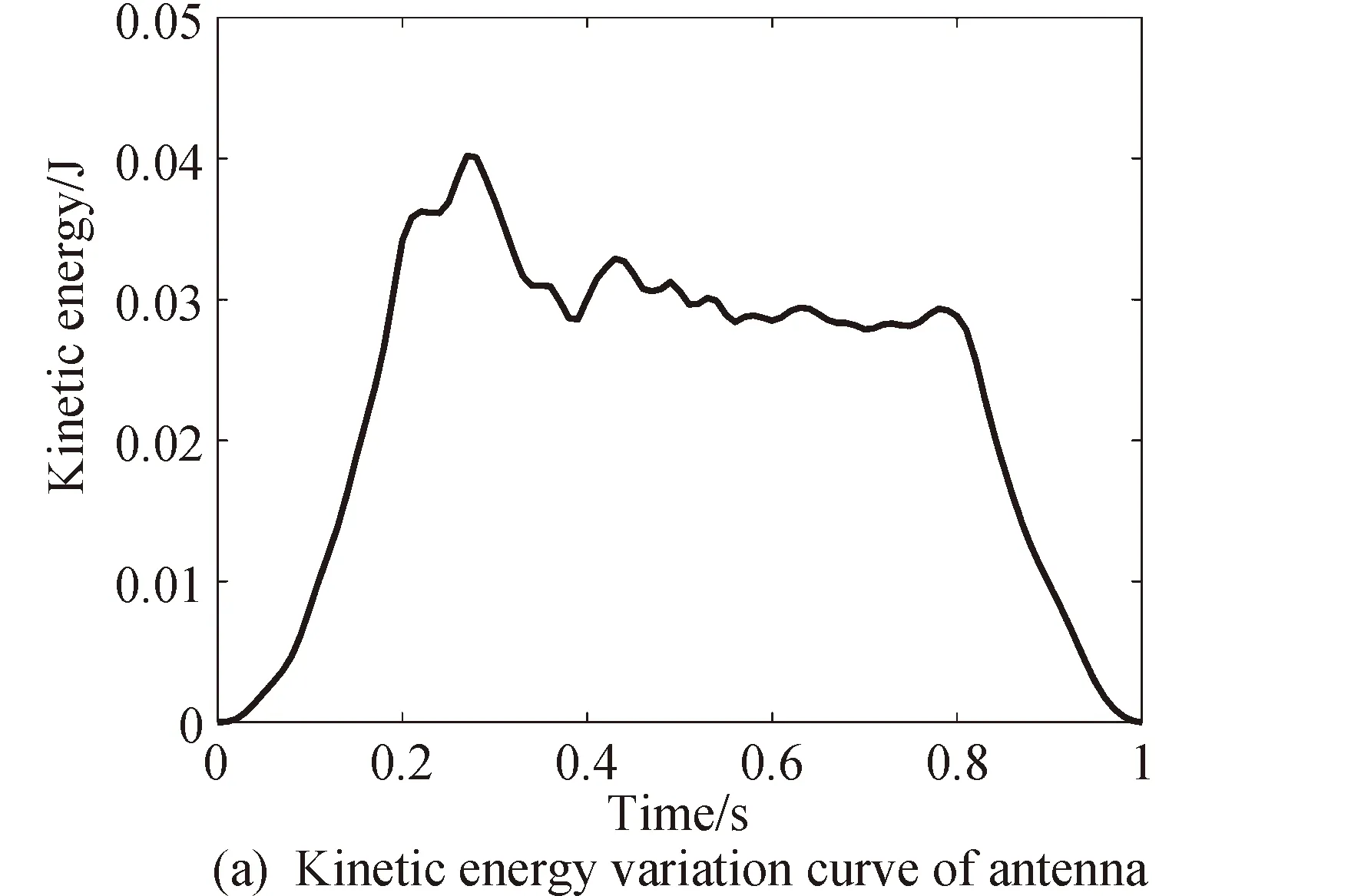
图11 天线系统动能和应变能随时间变化曲线

薄膜反射面上关键节点的位移曲线能够表征系统展开过程的动力学响应,这些节点的位移变化情况见图12(a～c)所示,如从位移曲线来看,节点P1、P2和P3位移曲线走势平稳,可知展开过程较为顺利且平稳性好。观察得知,P1沿三个方向的位移均大于其他两个节点位移,这是因为P1位于反射面最外环和肋的中间位置,变形最大。进一步地,分析关键节点的速度变化趋势,速度变化情况见图12(d～f),观察发现,速度曲线存在明显的震荡现象,由幅度来看,图12(d)中,P3处速度变化幅度较大,