基于人工蜂鸟算法的门式起重机主梁安全优化设计

肖 浩, 肖 林, 贺 宾, 赵章焰*,

(1.中交第二航务工程局有限公司,武汉 430040, E-mail:zzy63277@163.com;2.武汉理工大学 交通与物流工程学院,武汉 430063)

门式起重机是一种桥架结构由两侧支腿支撑、整机沿地面轨道运行的物料搬运设备,广泛应用于交通运输、建筑工地等领域。主梁作为整机的重要组成构件,其质量往往占整机质量的一半左右。传统主梁设计方法依赖于从业人员的经验,设计结果存在自重大、耗材高等问题。

伴随元启发式优化算法[1-7]的蓬勃发展,依托于智能优化算法的机械轻量化设计方法相继被提出。曾念寅等[8]以航用涡轮盘为研究对象,基于鲸鱼优化算法对涡轮盘进行结构尺寸优化;朱成实等[9]使用可变权重策略改进粒子群算法,将其应用于机床主轴优化设计中,在主轴刚度提高的前提下实现了体积减小。起重机结构轻量化设计方面,李志雄等[10]以结构3S(强度、刚度、稳定性)设计要求为约束条件,使用改进人工蜂群算法对桥式起重机主梁完成优化,获得了较为理想的设计结果;同约束条件下,Qi等[11]使用多镜面反射算法设计起重机金属结构,证明了该算法的工程应用能力。然而,3S设计要求仅为保证结构安全的最低限度,设计结果虽质量较轻,但在特定安全性要求下无法确保设计满足条件。除此之外,以上设计方法均无法向设计者直观展现设计结果的安全性。如若能在满足特定安全性要求的前提下对主梁进行轻量化设计,对我国制造业转型发展意义非凡。

鉴于此,本文通过三标度模糊层次综合评价法获得门式起重机主梁安全评分并将其加入优化模型约束条件中,基于人工蜂鸟算法获得结构轻量化最优解,为机械结构优化设计提供了一种全新的设计方法。

1 主梁安全评价

对主梁进行安全评价可量化设计结果的安全性,帮助设计者直观了解任意设计参数下主梁结构的安全程度,为后续构造安全性约束奠定基础。

1.1 门式起重机主梁安全评价体系

门式起重机一般包含两根主梁,各主梁上翼缘板铺设钢轨,小车在轨道上沿主梁轴向往复运动进行物品吊运。结合主梁失效形式[12]与结构特点,构建如图1所示门式起重机主梁安全评价体系。

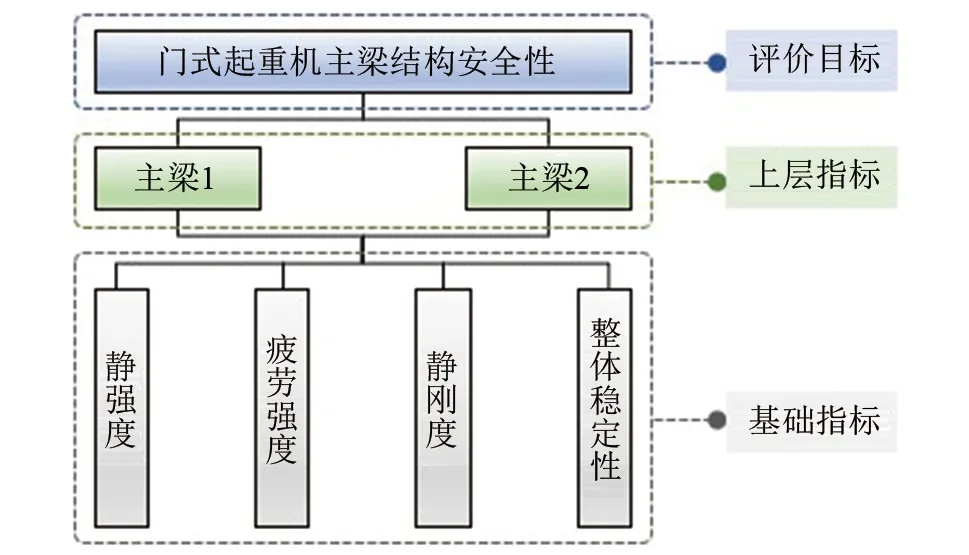
▲图1 门式起重机主梁安全评价体系

1.2 三标度模糊层次综合评价法

三标度模糊层次综合评价法[13]组合了三标度层次分析法[14]和模糊综合评价法,适用于处理多指标评价问题。

(1) 基础指标值计算

图3展示了主梁截面尺寸参数及应力危险点位置。z1～z4为主梁各板厚度,z5和z6为腹板高度与内间距。上下翼缘板宽度由z6及翼缘板外伸尺寸共同决定,一般主腹板侧上翼缘板外伸100 mm,其余各处外伸25 mm。危险点1～5为静强度验算点,6～9为疲劳强度验算点。使用极限状态法[15]和结构力学理论进行受力分析与计算,基础指标值的表征方式与计算方法如表1所示。

表1 基础指标值的表征方式与计算方法

(2) 隶属度计算

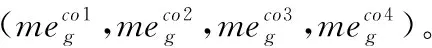
▲图2 门式起重机主梁受力简图

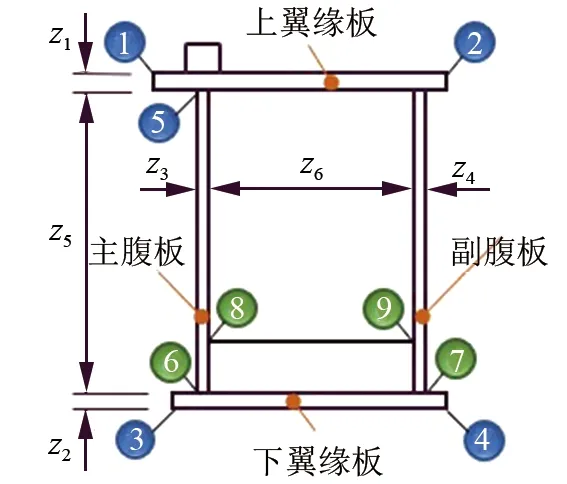
▲图3 主梁截面尺寸参数及危险点示意图

(3) 权重值计算

层次分析法[19]是一种条理化、系统化的主观赋权方法。传统层次分析法多为九标度层次分析法,存在因标度过多而引起计算量大、一致性检验复杂的问题。本文使用克服了上述缺点的三标度层次分析法,该方法关键在于将G项指标根据重要程度进行两两比较进而构造判断矩阵E=(eα,β)G×G。eα,β表示指标α相对于指标β对总目标的重要程度。已知判断矩阵后,通过优化矩阵计算与权重归一化操作,获得各指标权重集W=(w1,w2,…,wG)T。

(4) 模糊综合评价法

模糊综合评价法[20]可以对多因素、多属性评价对象进行定量评价。本文进行的综合评价属于二级模糊综合评价,需要将评价体系底层指标权重向量与隶属度矩阵进行式(1)点乘运算,获得一级模糊综合评价结果;然后将各一级评价结果组合为二级指标的隶属度矩阵与二级权重向量进行点乘运算,获得二级模糊综合评判结果。

EV=W·ME

(1)

(5) 评价分数量化

为使评价结果更为直观,使用评价分数体现评价结果。设置分数向量GR={90,80,70,60},采用式(2)计算评价得分。

RE=EVaim·GRT

(2)

式中:EVaim为目标层评价结果的隶属度矩阵。

2 人工蜂鸟算法

起重机主梁优化设计属于离散变量非线性优化问题,需选择先进智能优化算法进行变量寻优。人工蜂鸟算法(AHA)是一种模拟蜂鸟飞行与觅食行为的元启发式优化算法。其通过对蜂鸟飞行模式和觅食策略进行数学建模,从而实现目标优化。经对比验证,该算法具有全局搜索能力强和优化精度高等特点,适用于求解复杂非线性工程优化问题。因此,本文选用AHA算法作为结构优化的基础算法。

2.1 引导觅食

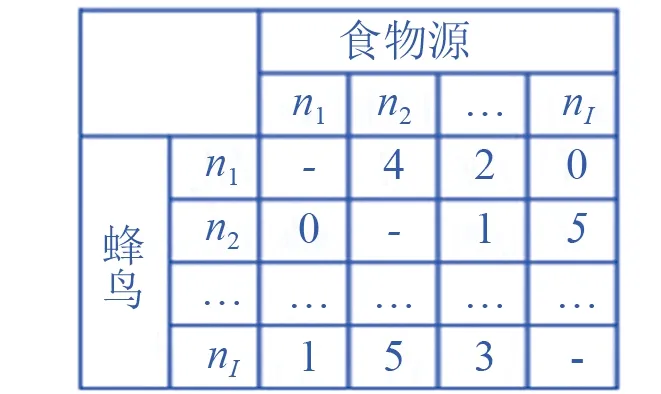
▲图4 AHA算法的访问表

在AHA算法中,各食物源作为解向量参与寻优操作,其优劣程度由函数适应度值表示。算法初期,每只蜂鸟飞向特定食物源进行觅食,随后保持自身位置与该食物源位置相同。此外,AHA算法还规定了各食物源的访问级别以此表征某个食物源未被访问时间和适应度情况。长时间未被访问或访问后适应度变优的食物源将被赋予较高访问级别。各食物源访问级别存储于图4所示I×I访问表中,表内第i行j列所存值表示第i只蜂鸟对第j个食物源的访问级别。当i=j时,表明该食物源为第i只蜂鸟自身所处食物源,其访问级别为空。

引导觅食是一种蜂鸟在最高访问级别食物源位置附近进行搜索的寻优策略。其数学表达式如式(3)所示:

(3)

c～N(0,1)

(4)

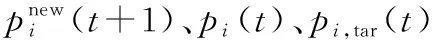
(5)

(6)

B=randperm(k),k∈[2,[r1·(D-2)]+1]

(7)

V(d)=1,d=1,…,D

(8)

式(5)为轴向飞行方向切换向量确定式,randi([1,D])可生成[1,D]内的随机整数;式(6)为对角向飞行方向切换向量确定式,该向量为一个随机生成的2～(D-1)维超矩形。式(7)确定了超矩形的维数,式中randperm(k)可创建[1,k]内的随机整数排列,r1为[0,1]内的随机数;式(8)为全向飞行方向切换向量确定式。在引导觅食和领地觅食搜索策略中,任意选择其中一种飞行模式进行食物源更新。

2.2 领地觅食

领地觅食是AHA算法的另一种寻优策略,此操作可使蜂鸟在其自身所处食物源位置附近飞行。其数学表达式为:

pi(t+1)=pi(t)+c·V·pi(t)

(9)

式中:pi(t)表示第t次迭代后,第i只蜂鸟所处食物源位置;pi(t+1)表示第i只蜂鸟更新后所处食物源位置;c由式(4)确定;V由式(5)～(8)确定。

领地觅食完成后,若更新后的蜂鸟所处食物源位置pi(t+1)适应度优于之前位置pi(t)的适应度,则该食物源的位置及适应度将更新。

2.3 迁徙觅食

迁徙觅食是算法后期避免陷入局部最优解的重要操作。当算法迭代次数满足迁徙条件(t=2n,n为种群规模)时,种群中适应度最差食物源位置的蜂鸟将在搜索空间内随机寻找新食物源,并将自身位置更新为新食物源的位置。迁徙觅食操作的数学表达式为:

pwor(t+1)=Low+r·(Up-Low)

(10)

式中:Up和Low分别为D维优化问题的上下限;r为[0,1]内D维随机数向量;pwor(t+1)为最差适应度食物源更新后的位置。

2.4 访问表更新

完成任意一种觅食寻优后,访问表将进行更新。对于引导觅食,当前蜂鸟目标食物源pi,tar(t)对应访问级别归零,其余对应食物源访问级别自增1个单位;对于领地觅食和迁徙觅食,当前蜂鸟对应食物源访问级别均自增1个单位。除此之外,若觅食后产生新位置的适应度变优,则所有蜂鸟对该食物源的访问级别设定为各蜂鸟最高访问级别的基础上自增1个单位。

2.5 算法寻优过程

人工蜂鸟算法寻优过程描述如下:

Step 1:设置算法相关参数,包括变量维数D,变量上下限Up和Low,种群规模n和最大迭代次数Maxt。

Step 2:初始化n个食物源位置即蜂鸟初始位置,并计算其适应度值。

Step 3:初始化每只蜂鸟对各食物源的访问级别并存储于访问表,令迭代次数t=1。

Step 4:各蜂鸟随机使用一种飞行模式按式(5)～(8)生成方向切换向量。

Step 5:各蜂鸟随机在引导觅食和领地觅食中选择一种方式,使用Step 4中生成的对应方向切换向量进行寻优并更新访问表。

Step 6:判断当前迭代次数t是否满足迁徙条件。若是,各蜂鸟执行迁徙觅食操作并更新访问表,否则继续执行Step 7。

Step 7:判断当前迭代次数t是否满足终止条件。若是,输出最优解信息;否则迭代次数t自增一个单位,返回Step 4继续运行。

3 主梁优化模型构建

本文优化模型建立如下:

(1) 目标函数

主梁自重轻量化为本文优化目标,门式起重机主梁为等截面实腹式箱型梁,其质量由式(14)确定。跨度一定,主梁自重轻量化即转换为截面面积最小化问题,因此目标函数确定为式(15)。

Massgirder=Agirder·Lspan·ρ

(11)

式中:Agirder为主梁截面面积,单位为mm2;Lspan为主梁跨度,单位为mm;ρ为钢材密度,单位为kg/mm3。

Agirder=z7·z1+zg·z2+z5·z3+z5·z4

(12)

z7=z3+z4+z6+125

(13)

zg=z3+z4+z6+50

(14)

式中:z和zg分别为上下翼缘板宽度,单位为mm。

(2) 设计变量

外部载荷与跨度确定时,主梁截面尺寸是主梁质量变化的唯一影响因素。因此将主梁截面参数尺寸Z(z1,z2,z3,z4,z5,z6)作为设计变量。

(3) 约束条件

主梁安全优化约束条件汇总于表2。

表2 主梁安全优化约束条件汇总表 单位:mm

4 工程实例

本文以如表3所示的在役30 t-25 m门式起重机为研究对象,进行主梁安全优化设计。

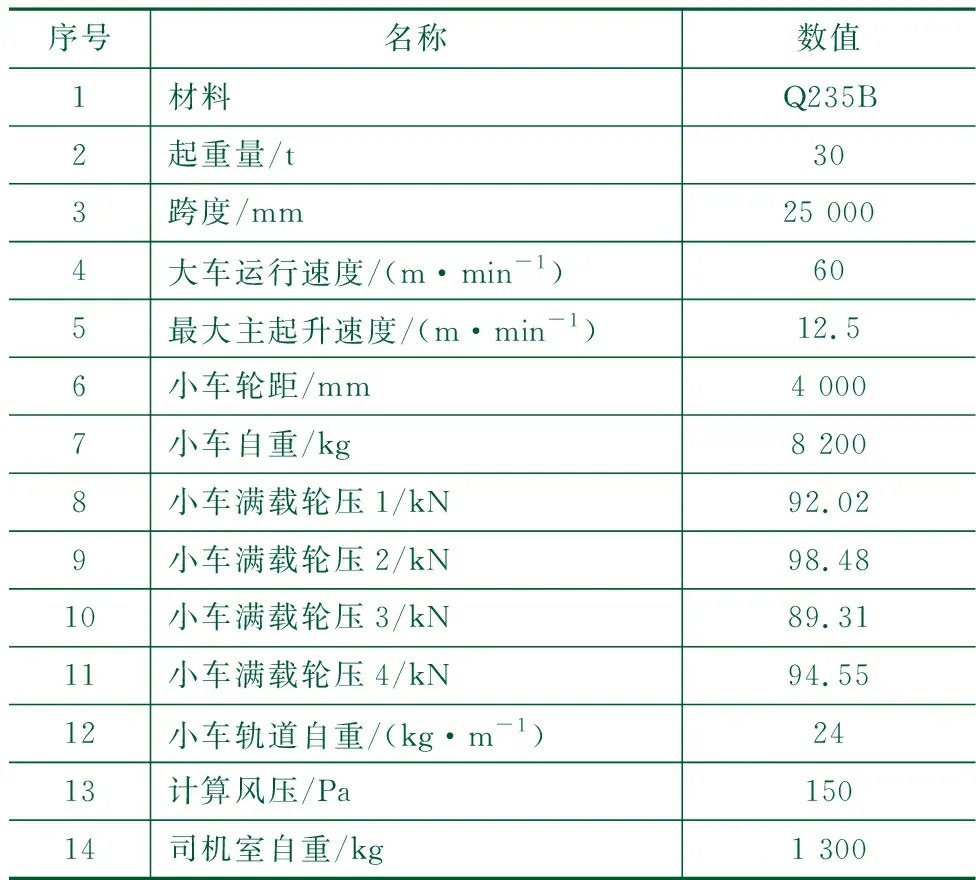
表3 30 t-25 m门式起重机基本参数

(1)安全评价各层指标权重确定

经专家评定,基础指标和上层指标的比较矩阵建立结果如式(18)和式(19)所示。三标度层次分析法计算各层权重结果为:W1=(0.4,0.4,0.1,0.1),W2=(0.666 7,0.333 3)。

(15)

(16)

式中:Ma1为基础指标的比较矩阵;Ma2为上层指标的比较矩阵。

(2) 隶属度函数上下限确定

表4中各基础评价指标梯形型分布函数上下限确定方法通过参考行业标准和咨询专家产生,各指标的最低下限为相应指标的许用值,之后通过近似定数等分的方式完成其余界限的确定。

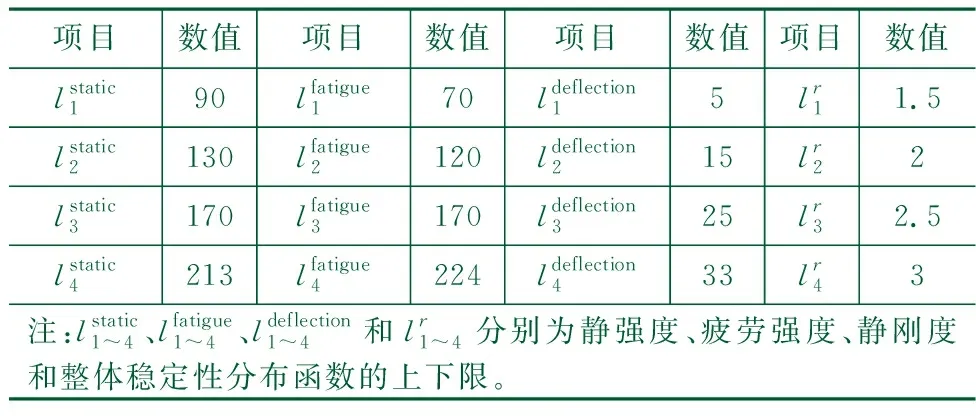
表4 隶属度函数上下限确定结果

(3) 结构安全优化设计

优化设计相关参数设置列于表5,结构安全优化的寻优结果展示于图5。

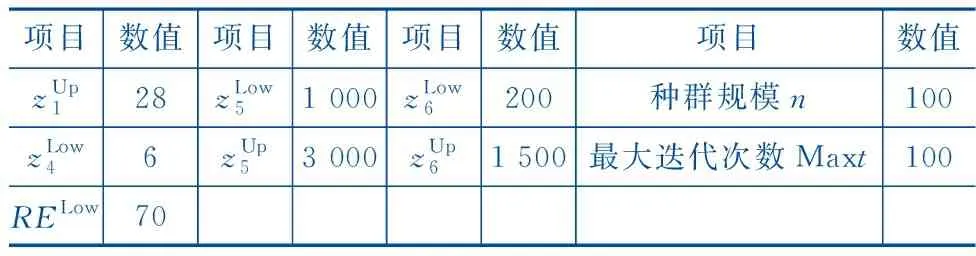
表5 优化设计相关参数设置

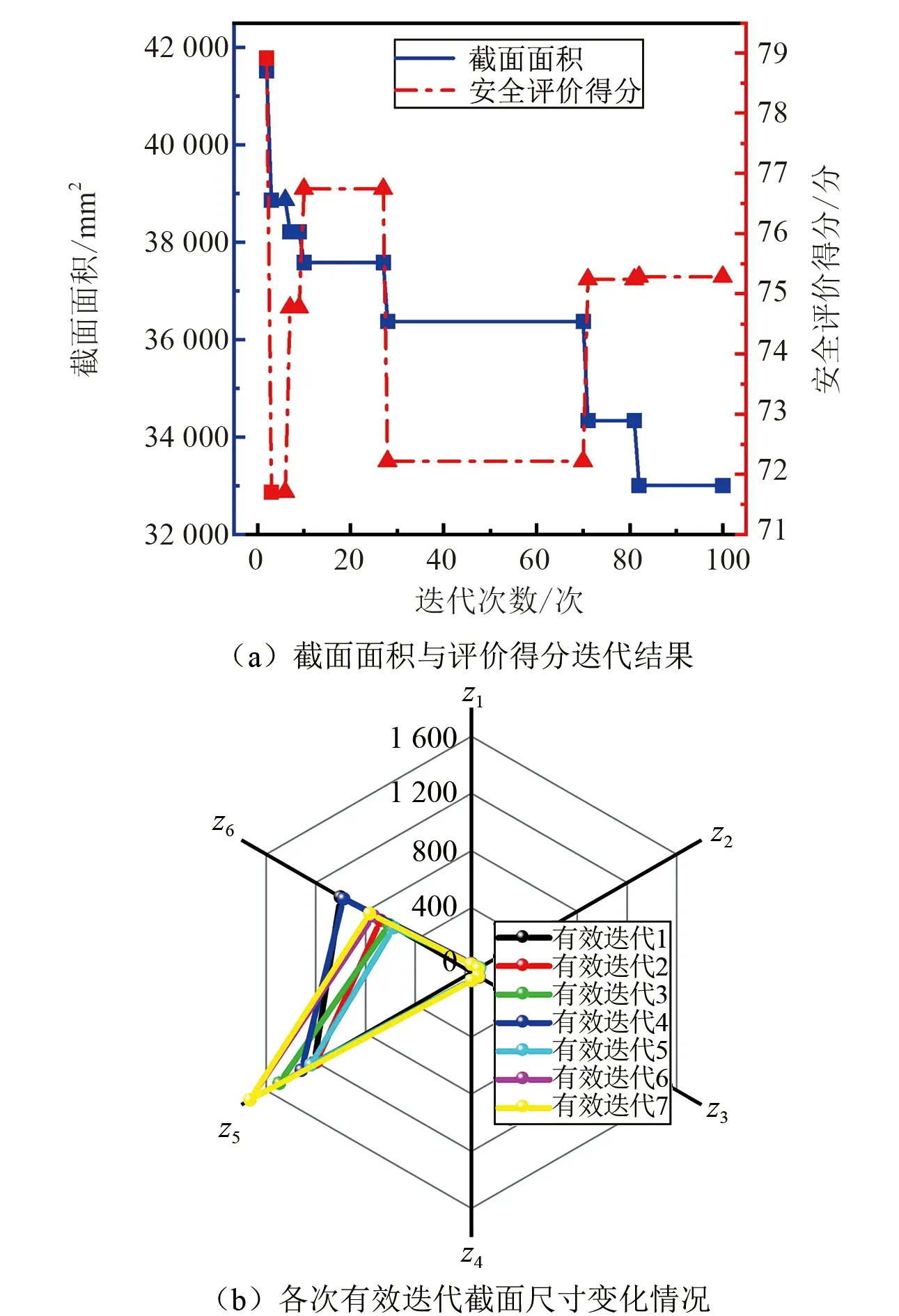
▲图5 结构安全优化结果

由图5可见,人工蜂鸟优化算法获得了当前终止条件下的最优设计参数,证明了该算法具有获得优化解的能力;安全评价得分与主梁截面面积变化趋势并不同步。例如图5中标记的两组数据(具体设计参数见表6),前者截面面积虽大于后者,但其安全分数却小于后者。这是因为由数据1确定的上下翼缘板厚度较大而腹板高度较低、腹板内间距较小,进而导致截面垂直方向和水平方向的惯性矩较小,其中数据1垂直和水平惯性矩计算结果分别为9.698 7×109mm4和2.197 6×109mm4,数据2的垂直和水平惯性矩分别为1.509 4×1010mm4和3.717 6×109mm4。较小的惯性矩在力学计算中会导致截面应力和整体结构挠度较大,因而安全评分较低。由表6可知,最终优化结果在保证安全分数大于70分的条件下,实现了截面面积优化。相对于原设计截面面积优化率为29.74%,安全分数仅降低5.31%,保证了结构自重大幅减轻的情况下安全分数小幅降低。

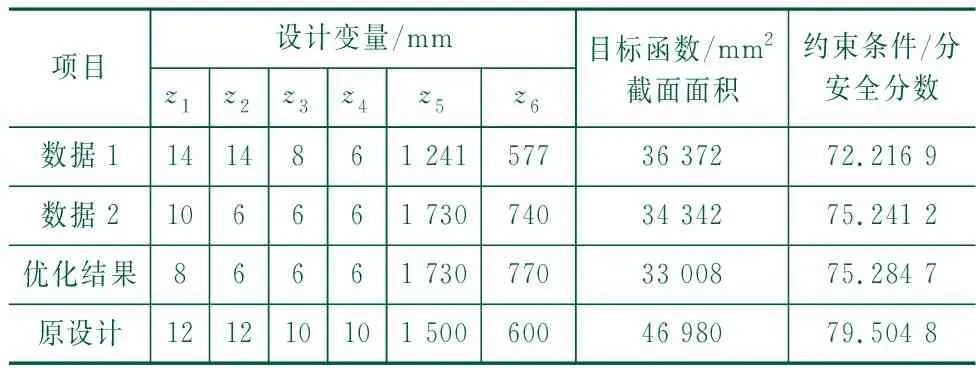
表6 各截面设计参数

5 结论

提出一种基于人工蜂鸟算法的门式起重机主梁安全优化设计方法,克服了以往设计方法自重大、耗材高、结果安全性不直观、无法获得特定安全要求下最优解的问题。通过构建安全约束下的主梁优化设计模型,使用人工蜂鸟算法对主梁截面参数进行寻优,获得了满足特定安全性的结构轻量化设计结果,提高了设计效率,降低了设计材耗。