基于物理模型和神经网络融合的表面粗糙度预测方法
2023-09-18钱思瑜张晟玮王成瀚苏沛源
钱思瑜, 张晟玮, 官 威, 王成瀚, 苏沛源, 沈 彬*,
(1.上海交通大学 机械与动力工程学院,上海 200240 ,E-mail:qsy18768036306@sjtu.edu.cn;2.中国航发成都发动机有限公司,成都 610503;3.沪东重机有限公司,上海 200129)
表面粗糙度是评价表面完整性的重要指标之一,零部件的疲劳寿命随表面粗糙度的增大而降低[1]。目前,离线测量仍然是工件表面粗糙度的常见测量方法。然而,复杂零部件的表面粗糙度离线检测成本高,效率低[2],不仅大大延长了零部件的制造周期和加工成本,也难以实时有效地为制造、检测过程提供经验和指导。
近年来,由于传感器技术和建模方法的进步,通过对表面粗糙度的实时预测和控制来优化制造工艺成为可能。在加工过程中进行表面粗糙度的预测,不仅能为切削加工的工艺优化提供借鉴,同时,也能够为后续的检测提供指导。
目前对零件表面粗糙度的建模预测方法可以大体分为三类:实验模型、理论模型、人工智能模型。随着对表面粗糙度预测精度、实时性需求的提升,单一种类的建模方法在发展过程中都体现出了局限性。实验模型[3-5]通过对实验数据进行分析,建立回归模型,所得的结论很少或没有普遍适用性;理论模型[6-7]从加工动力学、刀具特性、切屑形成机理等加工理论入手,建立表面粗糙度预测模型。但理论模型基于一些简化假设,实用性较低,通过理论模型进行有限元计算的方法在消耗大量的计算成本的同时,难以考虑加工过程中的动态因素,无法实现实时性预测;人工智能模型[8-9]采用种类繁多的机器学习算法,在大批量数据处理和非线性系统的拟合方面能力突出,能够在特定场景下实现对表面粗糙度的在线预测,但是其结果缺乏必要的可解释性和物理一致性[10]。
在切削加工领域,国内外一些学者观察到物理模型与数据方法的局限性,并尝试通过模型融合优化加工过程的监控手段。Rahimi[11]混合机器学习和基于物理的模型的预测结果来监测颤振;Wang[12]提出了一种交叉物理数据融合(Cross Physical-Data Fusion, CPDF)方案作为建模策略对刀具磨损进行预测。
目前,将物理模型与神经网络模型融合并应用于切削加工的表面粗糙度预测的研究鲜有报道。本文提出了一种物理模型与神经网络模型深度耦合的融合模型,实现对铣削加工过程表面粗糙度的精确预测。借助卷积自编码器对铣削振动信号进行高效动态特征提取,建立实时精准的数据集。铣削加工的物理模型从运动学角度解析了表面形貌形成过程,神经网络模型从数据的学习过程中实现对铣削过程动态特性的拟合,在两者优势结合的基础上最终实现高精度、高实时性、高解释性的表面粗糙度预测,为质量检测与工艺优化过程提供有效指导。
1 融合模型建立
1.1 物理模型
本文主要在文献[13-14]等的基础上,考虑铣削加工过程和与神经网络模型的结合性,基于下述简化假设,提出以下运动学模型以计算表面形貌及表面粗糙度。
(1) 刀具主轴与切削平面始终处于垂直状态,主轴不存在任何偏角;
(2) 工件与刀具均视为刚体,即忽略工件与刀具切削过程中的弹塑性形变影响,以及刀具磨损等刀具几何轮廓的变化;
(3) 在切削过程中切削参数始终为定值,暂不考虑由于工件材料不均匀等复杂因素对这些设定参数的动态影响。
建立以工件未铣削表面顶点为坐标原点的坐标系,加工表面的法向为z方向,进给方向为x方向。后续的推导和计算均为该坐标系下的计算结果。
1.1.1 刀具轮廓模型
针对可转位立式铣刀,刀具轮廓可简化为如图1所示的直线与圆弧的组合,主要的几何参数已在图中标注。
首先分别以实线和虚线的形式标注了切削前后的基准面,这两者的垂直距离即为切深ae,对于刀具本身而言,记切削刃数量为K,铣刀的半径为R,切削刃的半径为r,即上图模型中的对应圆弧部分,后切削刃角度记为Ф,铣刀后切削刃的部分由圆弧和与之相切的直线部分所构成,记铣刀直线起始点相对切削后表面高度为H。其余有关切削过程的参数分为记为:进给速度vf,主轴转速ns,每齿进给量fz。
L为切削刃部分扫掠的弦长,根据切削刃的铣刀直线部分起始点高度H与切深ae之间的关系,弦长有以下几种不同的计算方式:
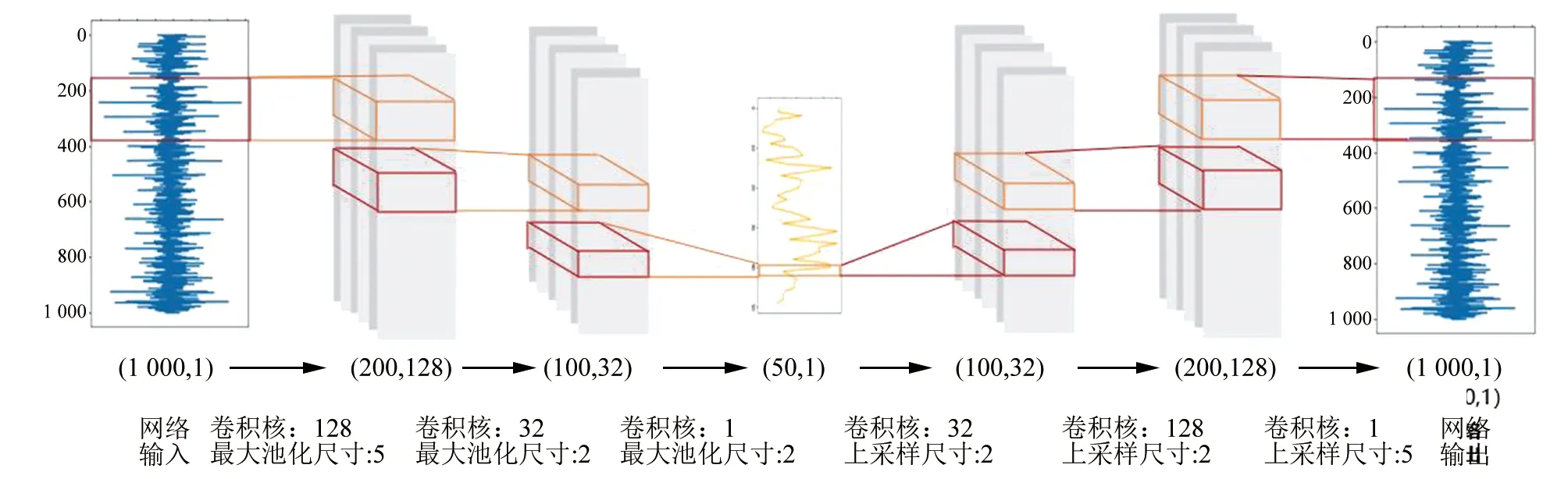
(1)ae 此时弦长仅与圆弧切削刃部分相割: ▲图1 扫掠弦长示意图 L1=2rsinφ-2(H-ae)cotφ (1) (2)H 此时弦长与圆弧和后切削刃的直线部分相割: (2) (3)ae>r: 此时弦长与主切削刃和直线部分相割: L3=[ae-r(1-cosφ)]cotφ+r(1+sinφ) (3) 弦长的计算主要用于通过对比弦长与进给速度的关系划分不同的几何关系,分类计算粗糙度轮廓。 1.1.2 基于运动学的粗糙度轮廓 进给速度,切削刃的几何形状和切削深度将对形成表面的粗糙度轮廓或纹理轮廓产生影响。通过比较H、ae的关系,以及fz和L的关系,总共有四种不同的状态和三种不同的几何形貌情况分类. 对于任意给定的切削参数和切削刃位置,即可获得对应切削过后的表面几何轮廓,只需确定不同时刻切削点的坐标,进而就可以获得任意时刻切削刃的位置,从而计算出整个切削表面的几何轮廓,易知每一个刀片上的任一点在切削运动中所经过的运动轨迹均为螺旋形(忽略物理过程及刀具磨损等现象)。设当前时刻为t,则切削点的横纵坐标可以算出: (4) (5) 1.1.3 表面粗糙度Ra值计算 轮廓算数平均差Ra是衡量表面粗糙度的常用指标之一。其物理意义是在取样长度L的测量范围内,轮廓曲线上的各个点到轮廓中线距离(即轮廓偏距)绝对值的算术平均值[15]: (6) 因此,对上述建立的表面形貌进行取样,以获取对应位置的Ra值,能够对整个表面的粗糙度进行表征。 本方法构建的物理与神经网络的融合模型结构如图2所示。 ▲图2 融合模型结构示意图 根据振动信号的标定关系,在切削过程中,x方向所对应的是进给方向,y方向所对应的为切宽方向,z方向所对应的是切深方向,因此,x方向的振动将会影响实际切削过程中的实时进给量,z方向的振动将会实时影响切削过程中的切深。利用特征提取器分别提取x方向和z方向6 000个时间点(每个时间点为0.02 s)的振动特征,压缩成长度为300的特征向量,以此作为上述融合模型的输入。 融合模型的第一部分是修调拟合层:由两个层数和神经元数相对较小的多层感知机组成,两个MLP(Multilayer Perceptron,MLP)分别以x方向和z方向的振动特征向量为输入,以进给和切深的修调量为输出。 然后是融合了数据模型的物理融合层:从MLP中获得进给和切深的修调量拟合值后,带入1.1节所述的物理模型进行计算,本文选取在进给方向上,刀具底面圆心所在直线上长度为一个进给量范围的Ra值,作为该工况下的表面粗糙度表征。 最后一部分是利用神经网络进行表面粗糙度值的阈值调节和映射。由于融合模块中最终采用的是中轴线上的几何轮廓的Ra值,而在实际的数据集制作中难以准确对对应位置的Ra值进行采样,且此处的Ra值仅能作为特征表征,不能直接作为铣削表面的Ra值。因此,此处再次通过小型的多层感知机网络,对Ra特征值向表面粗糙度Ra值进行映射,同时,此处引入MLP能对Ra值的取值范围进行调节。 融合模型最终输出的是表面粗糙度的预测Ra值。建立损失函数,计算预测值与测量值之间的误差,以均方误差最小化为指标优化模型参数。此表面粗糙度融合模型本质上是利用1.2 s范围内的振动数据动态特征修正静态运动学模型。 为对上述融合模型进行验证,通过高温合金侧铣实验研究了此模型表面粗糙度的预测能力。 实验在斯达拉格LX051五轴叶片加工中心机床上进行,选用材料为高温合金,所选试样的长度为150 mm,宽度为80 mm,中间有效切削部分(除去两端夹持部分)的长为100 mm,宽为80 mm,刀具为可转位立式铣刀,刀具参数及切削参数如表1所示。 表1 刀具参数与加工参数 加工过程的原始振动信号由贴附于机床主轴的三向振动信号传感器,通过NI采集卡,以5 kHz的采样频率进行采集。 将一个加工过程定义为铣刀从试样沿宽度方向切削至另一侧,整组实验共包含320个加工过程。每一个加工过程结束后,用三丰SJ210便携式表面粗糙度测量仪对前五分之一的切削部分的矩形区域,随机选取三个测量位置进行测量,以三个测点的Ra算术平均值为该区域表面粗糙度的表征数据进行记录。 将三向振动传感器采集到的原始振动数据,依次进行剔除异常值、填充缺省值、归一化的标准化处理。然后训练卷积自编码器对振动信号的动态特征进行有效提取,建立表面粗糙度预测的数据集,见图4。 ▲图3 铣削工件及部分参数示意图 ▲图4 卷积自编码器结构示意图 通过训练的卷积自编码器的特征提取部分,能够将输入的长度为1 000时间点数据,编码输出为长度为50的特征向量,再将这些特征向量进行解码,重构成输入数据相同长度的信号。重建误差绝对值的平均值为0.025 7,约为原序列平均值0.448的5.74%。选取其中x、z方向的振动信号各一组为例,重建结果与原数据之间的对比如图5。据此可以说明,训练的自编码器能够对振动的特征进行有效的提取。 截取训练完成卷积自编码器的前半部分作为特征提取器(输入长度为(1 000,1),输出长度为(50,1)),分别选取单个加工过程的前五分之一范围x、z方向的振动信号,标准化处理后,每个方向以6 000个原时间点数据(对应时间1.2,对应的加工范围与粗糙度检测范围一致),即特征提取后的一对300个数据点的特征向量与测得的Ra值相对应,最终制成含320组数据的表面粗糙度训练标签数据集。 将含320组标签数据的数据集按25∶7的比例划分训练集和测试集,训练集用于寻找网络的最优化参数,通过测试集验证网络的泛化能力以及避免网络过拟合的情况。模型训练选用Adam最小化损失函数,学习率设置为1×10-3,并以1×10-7的速度动态递减,使得学习率能够根据训练过程进行自适应减小,在训练初期加快训练速度。损失函数为MSE(Mean Squared Error),以2 000个epoch为训练量进行训练,对数据集上的预测结果进行分析如图6。 ▲图5 振动信号重建结果 ▲图6 表面粗糙度预测结果 图6(a)为训练集上的预测结果,共计250组训练集数据,其平均预测相对误差为4.48%,图6(b)为测试集上的预测结果,其平均预测相对误差为5.67%。将预测误差以折线图和条形统计图的形式绘制可以更清晰看到对比结果,如图6(c)、6(d),其中,绝大部分的误差均落在了±10%的相对误差范围内,以10%为允差范围,则预测的准确率为84.29%,考虑到数据集生成过程中,表面粗糙度的测量由手持式的表面粗糙度仪完成,其本身的测量过程就存在着一定的测量误差,因此,该准确率相对较高,能够充分说明该融合模型对表面粗糙度的预测能力。 本文提出了一种基于物理模型和神经网络融合的铣削表面粗糙度预测模型,通过卷积自编码特征提取器提取加工振动信号的数据特征后,修正运动学模型中的每齿进给量与切深,使静态的运动学模型能够被实时动态数据所驱动和优化,并利用多层感知机作为回归器,建立融合模型,实现了铣削过程的表面粗糙度Ra值的精准预测。通过高温合金侧铣实验主轴振动信号的采集和分析处理,验证了上述模型,得出以下结论: (1) 在现有表面轮廓运动学模型的基础上进行优化改进,根据加工参数和刀具几何参数之间的关系,分别建立不同切削情景下的加工表面形貌以及表面粗糙度Ra值计算的物理模型; (2) 建立了基于卷积自编码器的无监督数据特征提取器,能够将输入时间窗长度为6 000的切削振动数据压缩至300维,该卷积自编码器重建误差绝对值的平均值为0.025 7,相对重建误差为5.74%,有效提取了振动信号数据特征; (3) 用上述特征提取器,对振动信号特征进行提取,结合粗糙度仪测量的粗糙度标签为训练数据,基于MLP搭建机器学习模型获得对进给和切深的修调量以优化运动学模型,建立融合模型对粗糙度Ra值进行预测,在训练集和测试集上均有较高的预测精准度,预测平均相对误差约为4.74%,以10%的相对误差为允差范围,预测准确度为84.29%,区别于传统数据模型,融合模型降低了对数据集的依赖,有利于拓展至更加复杂多变的实际加工场景中,能够为加工和检测过程提供有效参考。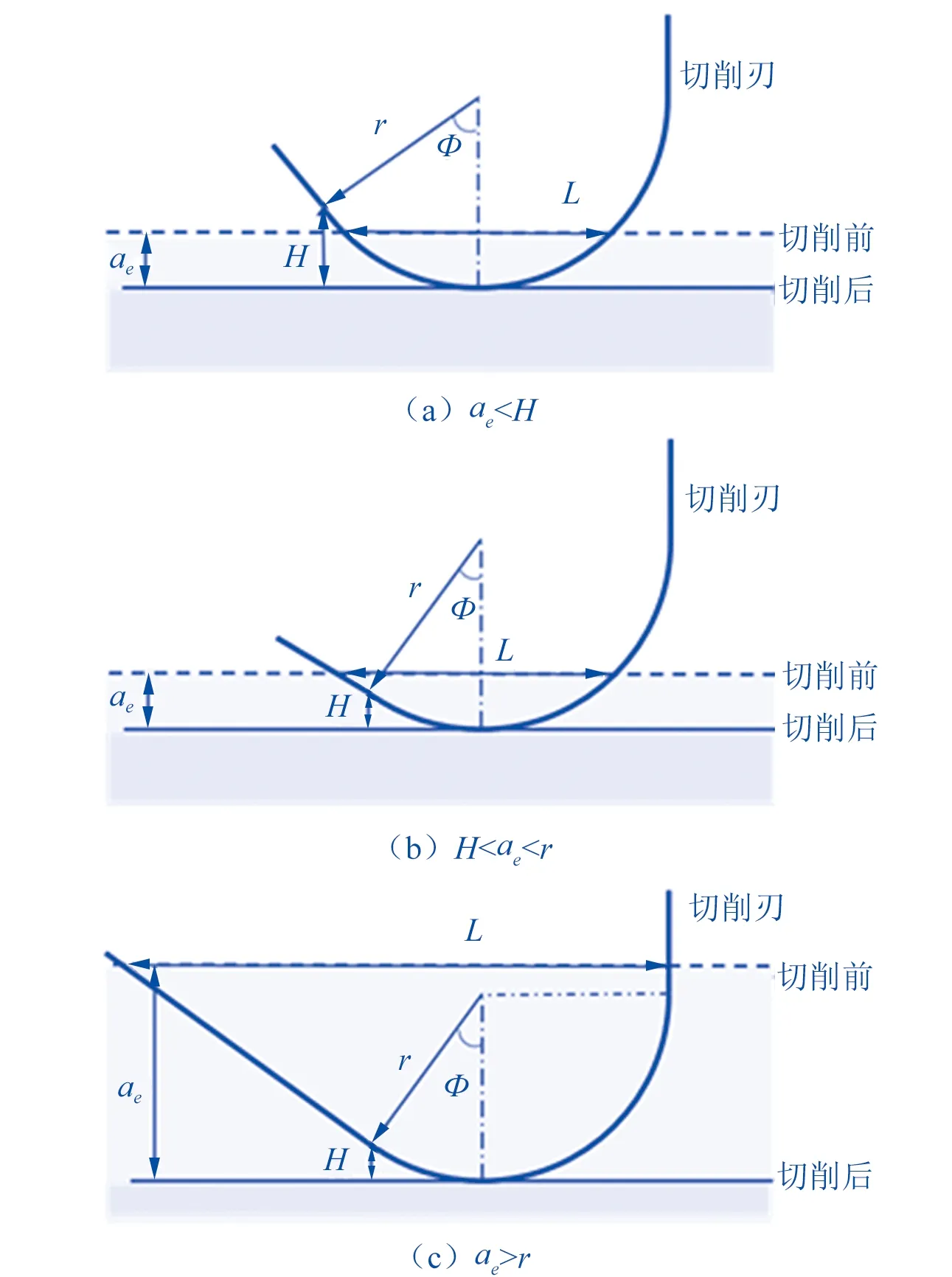
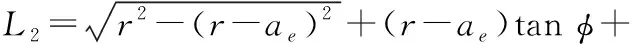

1.2 融合模型

2 融合模型验证
2.1 实验设计与数据采集

2.2 特征提取和数据集的建立

2.3 模型训练


3 结论
