基于高功率密度磁悬浮高速电机的全参数自适应控制

胡业发, 方康平, 吴华春*,,, 郭新华,3, 王念先

(1.武汉理工大学 机电工程学院,武汉 430070, E-mail: whc@whut.edu.cn;2.武汉理工大学 深圳研究院,广东 深圳 518057;3.湖北省磁悬浮工程技术研究中心,武汉 430070;4. 武汉科技大学 机械自动化学院,武汉 430081)

高功率密度高速电机由于体积小、质量轻、效率高等特点受到越来越多研究者的重视,运用也越来越广泛。在电动汽车领域,特斯拉Models所采用的310 kW、采用油冷方式的高功率密度感应电机被认为是目前世界上功率密度最高的感应电机[1]。2007年,美国国家橡树岭实验室研制了33 kW无刷混合励磁永磁同步电机。哈工大和郑州华联电动车辆,分别研制了20 kW和10 kW的永磁同步电机[2]。

而磁悬浮轴承是利用电磁力将转子悬浮起来的一种高性能的轴承,它具有无磨损、不需要润滑、寿命长等突出优点[3～6]。将磁悬浮轴承同高速电机相结合,能够极大地提升电机的功率密度和转速。随着磁悬浮技术在轴承和列车领域的广泛应用[7-9],研究者们对于将磁悬浮技术运用到高速电机中,也做出了很多尝试。D. J. B. Smith等人采用有限元法分析,提出可以在护套和永磁体间使用润滑剂来减少剪切应力[10]。J. M. Yon等人提出了一种能够极大程度减少涡流损耗的叠层绑扎结构[11]。张涛等人通过对面贴式和深埋式永磁转子的研究,验证了高速永磁转子在运转时能够有足够的接卸强度,并建立了铁芯桥厚度与转子转速的关系模型[12]。

但是磁悬浮轴承在运行的过程中,往往会受到各种扰动。并且电磁轴承-转子系统是一个开环不稳定系统,必须通过适当的反馈控制才能够稳定运行。所以针对磁悬浮轴承系统的控制算法研究显得尤为重要,也备受研究者们关注。目前,磁悬浮轴承系统的控制方法大致可以分为传统的PID控制、鲁棒控制、和智能控制。

传统PID控制器设计不依赖于被控对象的数学模型,在磁轴承的控制应用中较为常见。但是随着转子转速的提高,传统PID控制器不能很好地解决诸如磁悬浮轴承系统的陀螺力矩耦合、电磁场耦合、非线性特性等问题。研究者们针对这一问题,也进行了一些优化。2005年谷会东等人为有效抑制转子在一阶弯曲临界转速时转子的振动,于是在传统 PID 控制器的基础上添加了相位补偿器[13]。2008年B. X. S. Alexander等人在PID控制上添加了扩张状态观测器,并通过仿真比较论证了改进后的控制效果更优[14]。

对于鲁棒控制器,如H∞控制[15]、μ综合控制,控制器的求解需要事先获取被控对象精确的数学模型,为了设计一个满意的控制系统,必须事先掌握描述系统运动规律的数学模型及环境情况。1996年L Scott Stephens将μ综合与分析控制应用于磁悬浮系统用来抑制高速切削时的颤振[16]。Kenzo Nonami等以五自由度柔性转子为目标对象,设计了μ综合与分析控制器[17]。2002年R. L. Fittro等将μ综合与分析控制应用于多参数摄动的磁悬浮轴承中[18]。然而,通过动力学数学建模方法获取的精确的磁悬浮轴承系统,其阶次太高,使控制器的设计变得困难。

全参数自适应控制最初是由吴宏鑫院士在上世纪八十年代所提出的,其最开始是针对高阶线性定常对象,通过后来的研究发现该控制理论对于漫时变系统以及某些非线性系统同样适用。其在设计的时候并不依赖于精确的建模,可以较好地解决参数强时变、模型不确定性大等问题。能够有效抑制外来扰动,实现转子的稳定悬浮和运转。P Wurmsdobler于1996年研究了刚性转子的自适应控制[19]。Betschon F在1998年研究了自适应振动控制[20]。2018年南京航空航天大学的周宇研究了基于特征模型的磁悬浮轴承全系数自适应控制,在不需要精确数学模型的前提下完成了自适应控制系统的仿真模型,并进行了干扰仿真。本文建立了基于ACAC的特征模型,通过仿真分析和实验,验证了基于特征模型的全参数自适应控制方法能够有效抑制外来扰动,从而达到稳定悬浮和运转。

1 磁悬浮电机转子系统及建模

1.1 磁悬浮电机轴承-刚性转子不平衡建模

如图1所示为五自由度主动磁悬浮系统的转子受力简图,其中空间直角坐标系Ogxyz建立在转子的质心位置,x轴、y轴分别与重力反方向成45°夹角。φ为绕x轴转动角位移,θ为绕y轴的转动角位移,ωr为转子的转动角频率,Fz1、Fz2为沿着z轴的电磁力,a端为转子驱动端,b端为非驱动端。Fxa1、Fxa2、Fxb1、Fxb2为沿着x轴的电磁力,Fya1、Fya2、Fyb1、Fyb2为沿着y轴的电磁力,Og(xg,yg,zg)为转子质心,mg为转子重力。表1所示为磁悬浮轴承转子系统主要参数及其解释。

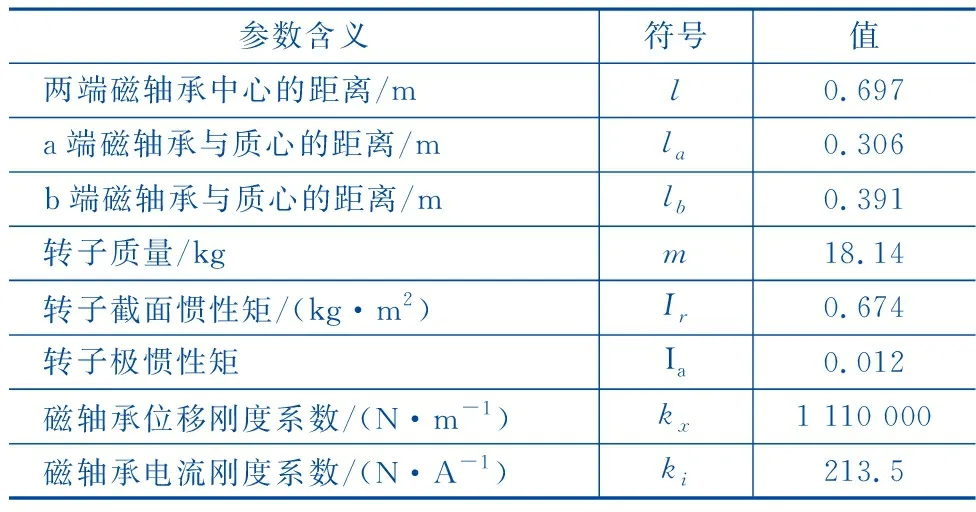
表1 主动磁悬浮轴承系统主要参数

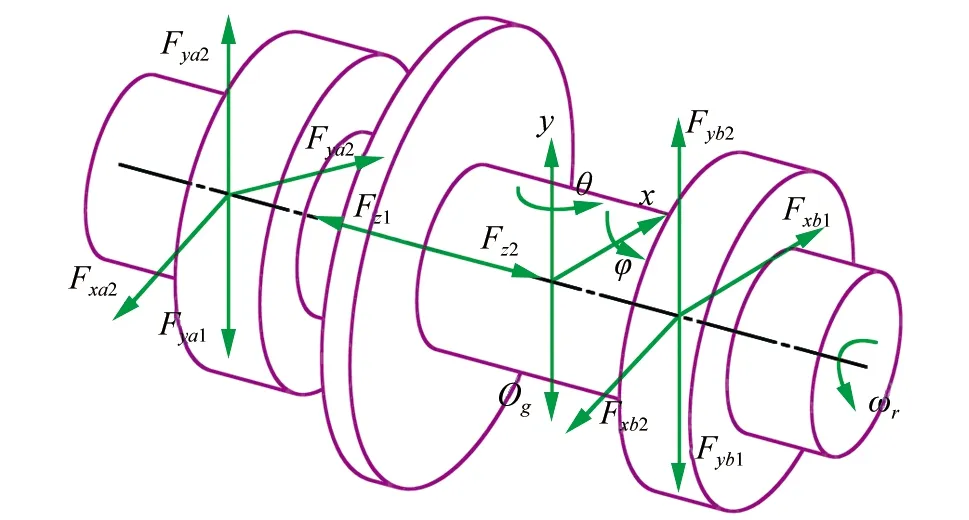
▲图1 刚性转子受力分析

根据图1受力分析及质点运动定理可以推出转子的运动微分方程如式(1):

(1)

式中:fx、fy为不平衡离心力在x轴、y轴上的分量,有式(2):

(2)

此外,式(1)中,Ir为转子直径转动惯量,Ia为转子极转动惯量,另外Te为电机输出转矩,目的是驱动转子绕z轴转动。

如图1中所示,有式3:

(3)

结合式(1)、(2)、(3)等,忽略重力影响,写出转子四个径向自由度的运动微分方程,如式(4):

(4)

为了分析方便,式(4)可表示为:

(5)

其中:

M为质量矩阵,C为阻尼矩阵,K为位移刚度系数矩阵,B为电流刚度系数矩阵,E为不平衡激励响应系数矩阵。分别如下:

(6)

式(6)是转子系统的二阶系统微分方程,将其转换成状态空间的形式。

(7)

令:

从而有:

求得各项系数为:

于是得到最终的状态空间方程为:

(8)

高功率密度高速电机使用的是电涡流传感器,具有非接触测量、频响宽、抗干扰能力强等优点,在实际使用时可以近似为一个比例环节[21]。令传感器环节的数学模型为:

本文所采用的功率放大器为两电平PWM开关功率放大器,本文忽略功率放大器的滞后并将其简化为:

Kamp=0.5 A/V

1.2 建立控制系统模型

本节将磁悬浮轴承,磁悬浮刚性转子,功率放大器和传感器动力学模型连接。如图2所示,为磁悬浮轴承-转子控制系统原理图。其中功率放大器接收控制电压信号μa输出控制电流ia,电磁轴承接收控制电流ia输出电磁力控制转子位移,位移传感器检测转子位移输出位移电压信号。

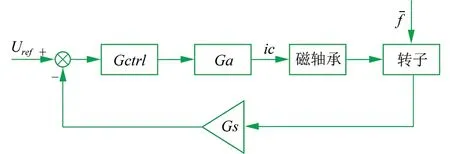
▲图2 磁悬浮转子系统控制原理图

结合状态空间方程、传感器和功放的增益,得到磁悬浮刚性转子不平衡控制模型:

(9)

2 全参数自适应控制设计

全参数自适应控制主要包括两个部分:(1)维持/跟踪控制(2)误差反馈控制。其中,维持/跟踪控制包括维持部分和积分部分。误差反馈控制包括黄金分割自适应控制和微分控制。

2.1 全参数自适应控制理论

全参数自适应控制理论中最重要的结论是全参数之和为1,其具体可以描述为:

若被控对象的动力学模型能够描述为如下微分方程的形式:

y(n)=an-1y(n-1)+an-2y(n-2)+…+
a1y1+bn-1μ(n-1)+…+b0μ

其离散化后的差分方程可以描述为:

y(k)=a1y(k-1)+a2y(k-2)+…+any(k-n)+
β0μ(k-1)+…+βn-1μ(k-n)

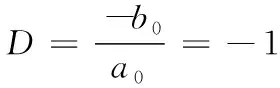
(2)当采样周期Δt→0,且a0和b0都不为0时:

根据估计参数计算所得控制量μc1,目的是为了让系统输出为设定值。积分部分μc2目的是为了消除系统的稳态误差,为磁悬浮转子系统提供一定的静刚度。磁悬浮转子系统本身是开环不稳定的,在自适应控制最初过渡阶段,特征模型参数估计未达到收敛时,系统的闭环稳定性难以得到保证,因此需要加入黄金分割自适应控制μc3来保证系统过渡阶段的闭环稳定性。微分控制μc4是为了改善系统的动态性能。即:

uc(k)=uc1(k)+uc2(k)+uc3(k)+uc4(k)

式中:

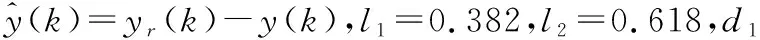
3 算法仿真分析

基于特征模型的全参数自适应控制的主要思想是通过在线辨识的方法将高阶系统的动力学特性以低阶特征模型的方式描述并提取出特征参数,然后将其反馈给全参数自适应控制器,不断的对被控对象进行自适应控制,以获得理想的控制效果。其控制系统的结构原理如图3所示。

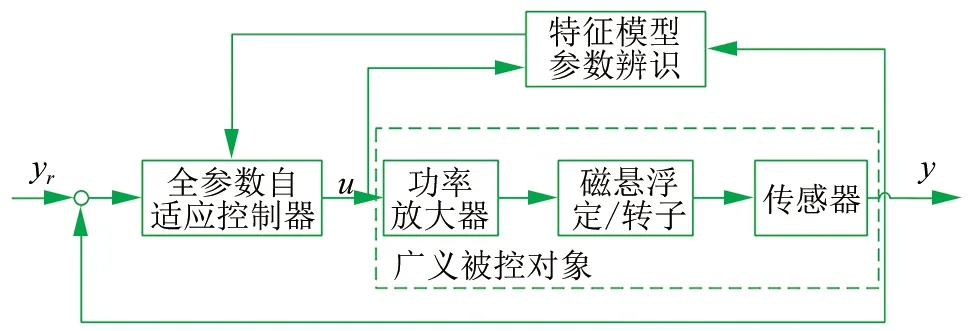
▲图3 全参数自适应控制器原理

3.1 转子阶跃响应

利用simulink建立磁悬浮转子四自由度控制模型[22],编写simulink S函数实现全参数自适应控制器仿真模型,并设置相应的传统PID控制器作为比较对象。以系统阶跃响应的超调量以及稳定时间为标准,采用试凑法获取动态性能最优的一组参数作为仿真的初始参数。最终选定初始值为f1(0)=2.102,f2(0)=-1.104,以及g0(0)=g1(0)=0.001,在每个控制通道中,估计特征参数的梯度自适应算法的参数选为δ=3.5与γ=1.5。由图4、图5所示的仿真结果可知,系统在基于特征模型的全参数自适应控制与传统PID控制下均有较快的响应,这说明全参数自适应控制有效。根据图中的数据还可以看出系统在基于特征模型的全参数自适应控制下,仅需要0.04 s即可达到稳态,而系统在PID控制下则需要0.09 s才能达到稳态。这说明前者控制下的磁悬浮轴承系统转子起浮速度明显快于后者,且超调较小。

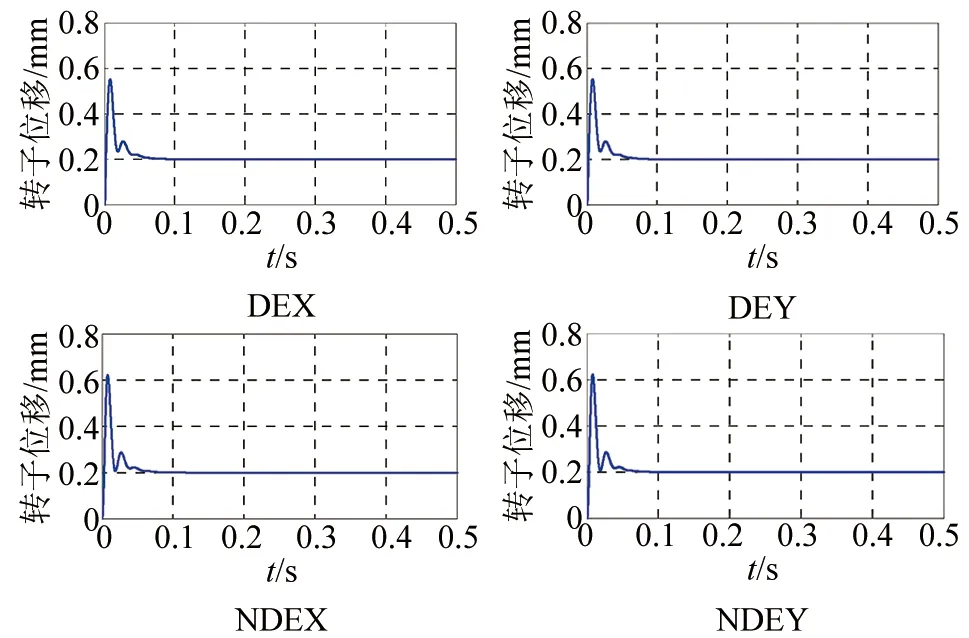
▲图4 PID阶跃响应

通过上述对四自由度磁悬浮轴承-转子系统的仿真,得到了自适应控制器的系统特征参量真值,其收敛值为f1=2.101,f2=-1.105,g0=-0.002及g1=-0.000 953。f1+f2+g0+g1=0.993 047≈1,与全参数自适应理论中特征参量和为1相符合。

3.2 转子不平衡响应仿真

在转子实际的运行过程中,转子振动主要形式是不平衡振动,其是与转速同频的正余弦波动。当转子起浮稳定在平衡位置后,对转子施加等效不平衡电流,分别得到PID以及全参数自适应控制下的不平衡响应即轴心轨迹如图6和图7。

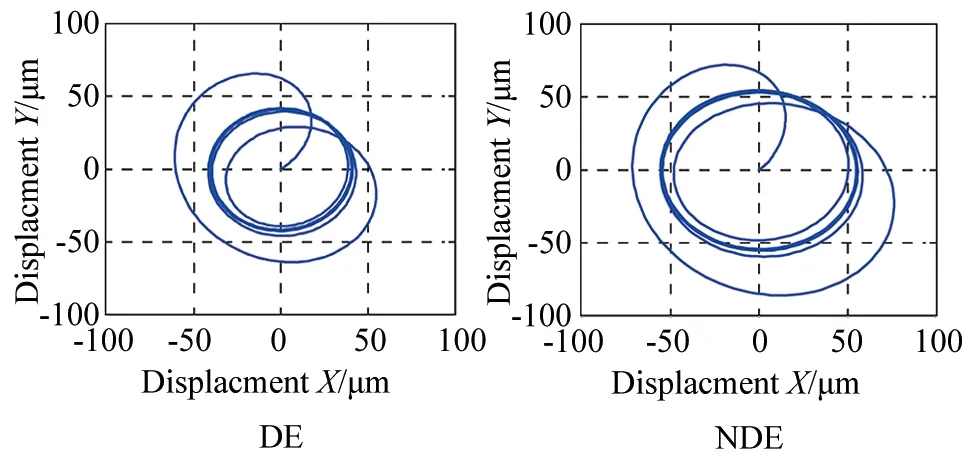
▲图6 PID不平衡响应

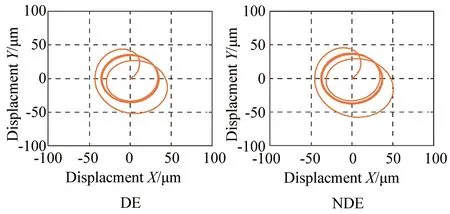
▲图7 ACAC不平衡响应

由图6和图7可知,在PID控制下,转子的轴心轨迹较大,即转子产生了较大的不平衡振动,驱动端和非驱动端的转子稳定振幅大小分别为41 μm与55 μm。在基于特征模型的全参数自适应控制下,转子的轴心轨迹相对PID而言较小,驱动端和非驱动端的转子稳定振幅大小分别为35 μm与37 μm。由此可见,基于特征模型的全参数自适应控制算法在对转子不平衡振动抑制方面比传统PID更好。

4 实验验证

为了验证全参数自适应控制算法对于磁悬浮轴承转子实际的控制效果,搭建了如图8所示的实验平台,该平台由电机、磁悬浮轴承、转子、功率放大器、快速控制原型机等设备构成。其中电机功率为1.2 kW,功率放大器的直流总线电压为50 V,开关频率为20 kHz。实验平台的转子由两端两个径向磁悬浮轴承支承,实现四自由度稳定悬浮。中间是用于对转子施加不同激励的磁悬浮轴承,但是在本文的实验验证部分并未得到使用。除却图中所示的设备外,还安装了四个电涡流传感器,用以测量转子在x与y方向的位移。

实验过程中,主要调节积分系数Ki、微分系数Kd以及参数λ,ACAC的积分系数Ki和微分系数Kd与传统PID控制理论中的相似。Kd通过抑制系统偏差的变化,达到改善系统动态特性的目的。而Ki可以消除系统的稳态误差,其值越大系统稳态误差消除越快。调节时需要注意λ对于系统存在一个稳定域,在这个稳定域内参数过大会引起系统的震荡,参数过小会造成系统的大超调量,但是λ对于系统的稳定时间的影响并不大[23]。图9中的(a)、(b)两图分别为实验得到的前后端静态悬浮曲线,可以看出悬浮精度在±5 μm以内。

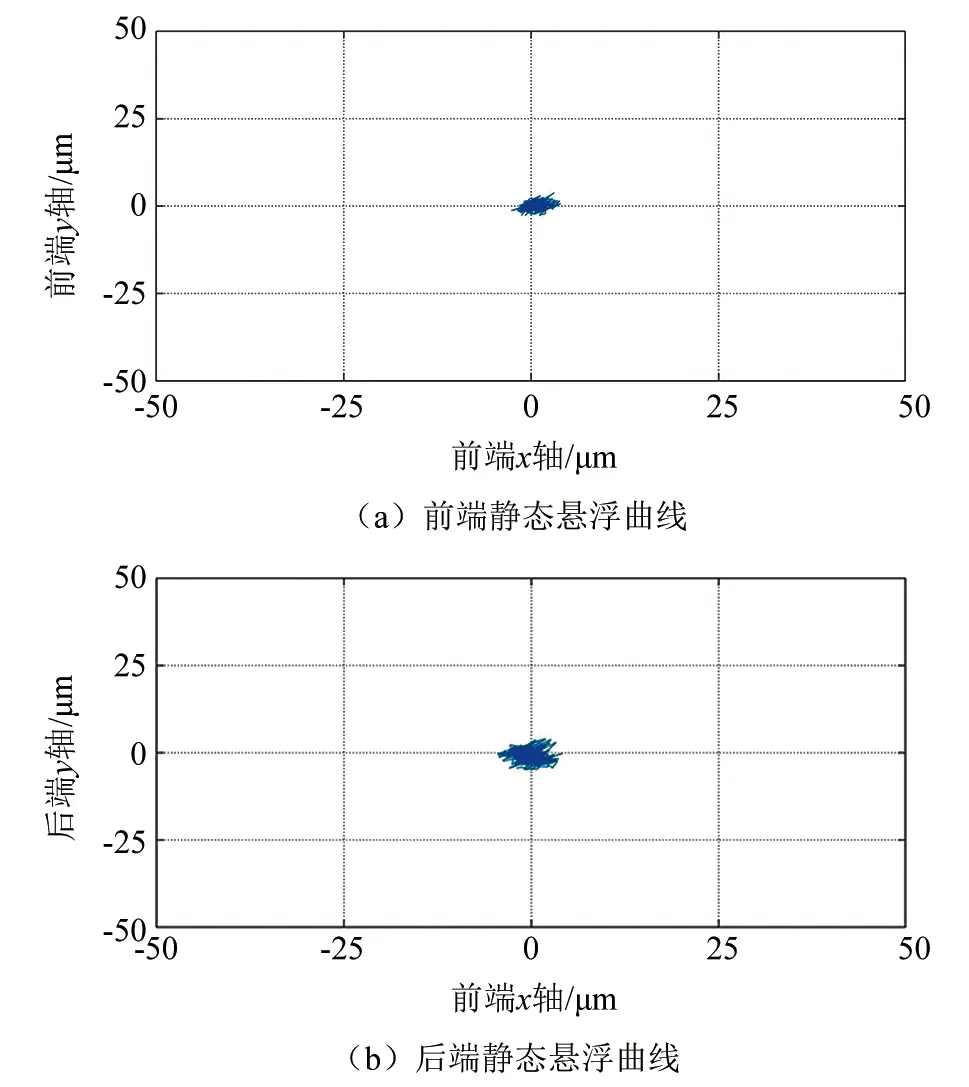
▲图9 悬浮曲线

从上述实验结果中可以看出全参数自适应控制算法能够对转子四自由度的起浮起到良好的控制效果,验证了本文提出的基于特征模型的ACAC实际应用的可能性。

4 结束语

本文以高功率密度磁悬浮高速电机为对象,描述了全参数自适应控制方法,建立了模型,并进行了仿真和实验。具体结论如下:

(1) 本文针对目标对象建立了磁悬浮电机轴承-刚性转子不平衡模型、控制系统模型,并设计了针对特征模型的全参数自适应控制器。从设计过程中可以看出全参数自适应控制的模型构建不依赖于精确的数学模型,能够有效的解决参数时变强、模型不确定性大等问题。

(2) 利用simulink搭建仿真平台,将自适应控制同传统的PID控制进行比较[24]。在基于特征模型的全参数自适应控制下,磁悬浮轴承系统转子起浮速度明显快于传统PID控制,并且超调较小。仿真对比实验的结果显现了全参数自适应控制的性能要优于传统PID控制。从不平衡响应仿真中可以看出基于特征模型的全参数自适应控制算法对转子不平衡振动抑制之后的转子振幅要小于传统PID控制之后的振幅。

(3) 利用实验室现有器材搭建了磁轴承转子悬浮实验平台,验证基于特征模型的全参数自适应控制对于转子静态悬浮的效果。从测试结果中可以看出,全参数自适应控制能够满足磁轴承转子的稳定悬浮。