基于ICEEMDAN与支持向量机的轴承故障诊断方法

王朝兵, 靳福涛, 张 龙, 熊国良, 颜秋宏, 乔 宇

(1.轨道交通基础设施性能监测与保障国家重点实验室,南昌 330013,E-mail:chaobing@163.com;2.中车戚墅堰机车有限公司,江苏 常州 213011)

滚动轴承作为现代机械中关键的基础部件,在高铁和轮船等交通工具中得到了广泛使用。其工作时若发生故障,可能会对机械设备造成局部损伤、甚至人员伤亡,轴承自身的健康状况对于机械设备的可靠运行有着重要影响[1]。因此对滚动轴承进行故障诊断、状态监测对安全生产、工业发展具有重要的现实意义。

在对轴承进行故障诊断时,由于振动波形易受到机械噪声的干扰,如何准确提取出其特征是识别轴承故障类型的基础。Colominas等[2]于2014年提出改进自适应噪声完备经验模式分解方法(Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise,ICEEMDAN)。该方法能够去除模态分量中大部分的残余量,从而获得较小的重构误差,同时消除了模态混叠等问题,获得了较好的重构结果[3]。杨洋等[4]提出ICEEMDAN与多尺度样本熵的心音特征,结合逻辑回归模型用于左室舒张功能障碍识别。随着ICEEMDAN逐渐应用到故障诊断的降噪处理中,Ziming Kou等[5]应用ICEEMDAN能量熵与SVM相结合,有效改善了矿井提升机的轴承故障识别率。此外,在各类故障识别方法中,熵值指标因其能反映出振动信号的复杂特性,常被作为特征向量使用。由于实际机车轮对轴承的振动信号往往呈非线性、非平稳特点,单一尺度下不能包含完整的故障信息,Costa等[6]在样本熵的基础上进行多尺度粗粒化改进,提出了多尺度样本熵(Multi-scaleper Mutation Entropy, MSE)的概念,反映时间序列在不同尺度下的自相似性和复杂程度,能体现出多个尺度上包含的故障信息。张龙等[7]通过在多个不同时间序列中分别计算它们的样本熵值,构造出MSE特征向量,实现轴承故障类型的分类。

在轴承的故障识别方面,深度学习[8](Deep Learning,DL)可以从海量的数据中提取到关键的特征对象,实现“端到端”故障诊断。但深度学习方法均需较大量的样本数据进行训练[9],对于真实的机车轮对轴承故障识别问题,由于故障样本量较少,因此在实际工程中表现欠佳。支持向量机(Support Vector Machine,SVM)作为小样本场景下被广泛应用的机器学习方法,具有速度快、准确率高的优点[10]。然而其分类性能易受到惩罚因子c和核函数参数g影响[11],因此有学者将各类优化算法用于SVM参数寻优。周建民等[12]使用遗传算法(GA)优化SVM参数,确定参数最优值。赵东升等[13]通过引力搜索算法(GSA)对支持向量机(SVM)的关键参数进行优化,构造了BGSA-SVM的分类模型。但上述算法存在易收敛到局部优值、寻优时间久等问题,难以满足对真实机车轮对轴承故障诊断的要求[14]。灰狼算法[15](Grey Wolf Optimization,GWO)涉及参数少、收敛快、不易陷入局部最优,易于实现,应用在SVM超参数寻优能够有效提高分类性能。

针对机车轮对轴承不同健康状态的分类问题,本文提出ICEEMDAN、MSE相结合的特征提取方法,应用GWO-SVM实现滚动轴承的故障分类。本文实验使用同组DF4型内燃机车轮对轴承的实际故障数据,同时与CEEMDAN-MSE+GWO-SVM、ICEEMDAN-MSE-SVM等方法进行比较验证。

1 基本理论

1.1 ICEEMDAN基本原理

传统的CEEMDAN方法,是将添加了自适应噪声的原始信号或残余分量,在一次迭代中进行EMD分析,并对所得到的IMF信息采用平均处理的手段,得出最后的IMF。ICEEMDAN相比传统方法,通过利用上一个迭代的残差值与本次若干个添加了自适应噪声的信号残余误差平均值的差额,得出了这个迭代的IMF分量,使分解后的虚假分量有所降低,进而减少了模态混叠的现象。

ICEEMDAN算法通过将高斯白噪声经过EMD分解后的第k个IMF分量作为新的特殊噪声Ek[w(i)],计算其在每个IMF上的局部均值,定义ICEEMDAN分解后的IMF为残差分量与局部均值的差值,以削减分量上的残余噪声。ICEEMDAN算法如下:

(1) 对原始信号x叠加可控噪声;

x(i)=x+β0E1[w(i)],(i=1,2,…,N)

(1)

式中:x(i)是构造信号;β0是噪声标准偏差;E1(·)为分解算子;w(i)是添加零均值单位方差的第i个白噪声。

(2) 计算构造信号x(i)的局部均值,并求其平均值即为残余分量r1:

(2)

其中:M1(·)为局部均值函数。

(3)计算第1个模态(k=1),即原信号x与第1个残余分量r1之差:

(3)

(4) 计算第k个模态(k≥2),即上一次计算的残余误差rk-1与本次残余误差rk的差值:

(4)

(5)

(5) 计算第k=k+1个模态,回到(4),直至满足迭代终止条件。

1.2 多尺度样本熵原理及其参数选择

样本熵是能够表征时间序列复杂性和非线性的测度指标,但其只能从单一尺度上进行熵值的特征计算,无法充分挖掘故障特征的信息。为了弥补该方面的不足,MSE算法被提出,其通过计算出序列于不同尺度上的粗粒化结构,求出各个粗粒化序列的样本熵值[16],从而表征时间序列在多个尺度下的自相似性和复杂程度,其计算过程如下:

(1) 对时间序列{x(i)}=x(1),x(2),…,x(N),定义粗粒化序列P(τ):

(6)

式中:尺度因子为正整数,即τ=[1,2,…,τmax],粗粒化序列长度为原时间序列的1/τ。

(2) 当τ取不同值时,计算P(τ)的SE值,即MSE:

(7)

MSE计算结果受m,r和τ的共同作用。嵌入维数越大则结果越精确,根据时间序列的长短,一般取2或3;r决定了模糊函数的边界宽度,常取原始信号的0.15倍标准差。在现实应用中,如果τ取值较小,就不能反映原始序列的复杂度;如果τ取值较大,则可能会丢失信息,故本文取最大尺度因子τmax=20。

2 灰狼算法优化支持向量机

2.1 灰狼优化算法

GWO是一种新型群体寻优算法,其寻优过程即模拟狼群相互配合、调整狩猎位置,逐步移动靠近、直至捕获猎物的行为。其过程如下:

(1) 包围。即模拟狼群搜索并接近猎物的行为,数学表达如式(8)所示。

(8)

式中:D为灰狼到目标的距离;t为迭代次数;A、C为协同系数,Xp为目标位置,X(t)为灰狼当前坐标;r1、r2为[0,1]的随机向量,α是收敛因子,随t增加而递减。

(2)狩猎。设α、β、δ3匹狼识别能力较强,故保留其位置信息,更新其他狼的位置,数学描述为:

(9)

式中:X为灰狼当前位置;Xα、Xβ、Xδ分别为α、β、δ狼的位置信息。

(3) 捕获。狼群狩猎的最后一步,头狼α代表的数据即为寻优结果。

2.2 灰狼算法优化支持向量机

SVM的目标是在输入特征空间上找到一个最优超平面对原样本尽可能多的进行正确分割,且使每类样本在该平面上的间距最大,并构成了一个约束二次规划问题,通过求解该问题,可以得到分类器[17],因其优异的分类性能和可靠性被广泛用于故障诊断领域。以RBF为核函数的支持向量机中,径向基函数的2个重要参数惩罚因子c和方差系数g,它们的取值对SVM的分类性能有着重要影响。

由于GWO算法收敛快、涉参少、全局寻优能力强等优点,运用该算法对超参数c和g寻优,以提高SVM分类精度。图1为GWO-SVM优化流程图:

(1) 初始化灰狼算法,设置狼群大小P、搜索维度T和最大迭代次数N等,并生成狼群初始位置,;

(2) 初始化支持向量机参数,以正确率作为适应度函数,设置c、g参数寻优范围;

(3) 输入数据,计算当前适应度值,由式(9)调整狼群位置并更新适应度函数值;

(4) 判断循环条件,迭代次数≤N时回到(3),否则退出循环,输出最佳参数c和g;

(5) 将寻优结果参数c、g带入训练SVM模型,保存最佳模型后并在测试集上进行故障分类。

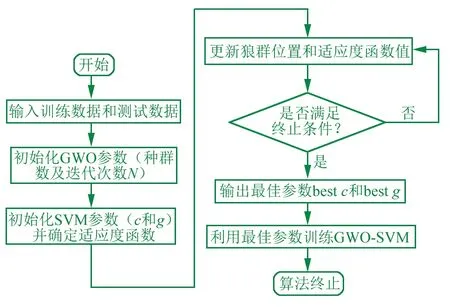
▲图1 GWO-SVM流程图

3 本文提出的机车轮对轴承故障诊断算法

机车轮对轴承产生的故障信号呈强非线性非平稳特性,通过对原始信号ICEEMDAN分解,将重构后信号的MSE值作为特征向量,以SVM为分类器进行轴承故障分类与识别。如图2所示,具体步骤如下:

(1) 采集机车轴承原始故障信号,进行数据处理;

(2) 对不同健康状态的原始信号进行ICEEMDAN分解得到若干组IMF分量,将大于相关系数阈值的IMF分量重构;

(3) 对重构后的信号计算MSE值得到特征向量,随机划分训练集和测试数据集;

(4) 构建GWO-SVM模型,初始化网络参数,设置核函数、惩罚因子等参数;

(5) 通过训练样本不断优化模型参数,得到训练好的诊断模型;

(6) 输入测试样本,最后通过分类器输出得到诊断的结果。

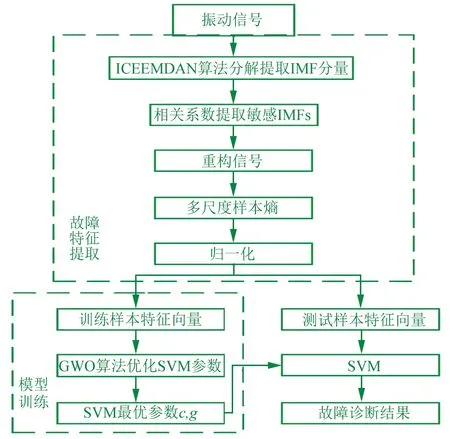
▲图2 故障诊断流程图

4 机车轮对轴承故障诊断实例分析

4.1 故障数据采集

为验证所述方法的有效性,本文实验在某局机务段的JL-501机车轴承试验台上完成,如图3所示。待测轴承安装在主轴箱上进行旋转动作;待测轴承通过液压系统实现进行径向的压力加载。电源为380 V,50 Hz三相四线交流电源,电机驱动总功率为5 kW,主轴转速范围为120 r/min～1 200 r/min,本次试验转速为500 r/min。

▲图3 JL-501机车轴承检测台

本文实验使用DF4型内燃机车装配的滚子轴承,型号为NJ2232WB,外径φ290 mm,内径为φ160 mm,故障均为列车实际运行产生,实验前对所有轴承进行了除污处理,以避免对实验结果的影响。本实验数据通过设置三通道(加速度传感器A、B、C)对机车轮对轴承进行信号采集,采样频率为20 000 Hz。对采集的7种机车轴承类型,并依次编号C1-C7,其中C1为正常轴承数据,如图4为每种故障类型所对应的机车轴承。

▲图4 六种机车轮对轴承故障类型

为避免数据集划分对检测结果的影响,在每种状态下70组样本中,随机选取55组共计385组数据为训练样本,每种类型剩余15组,共计105组数据为测试集。设置7种工况的训练集状态标签依次为1、2、3、4、5、6、7。

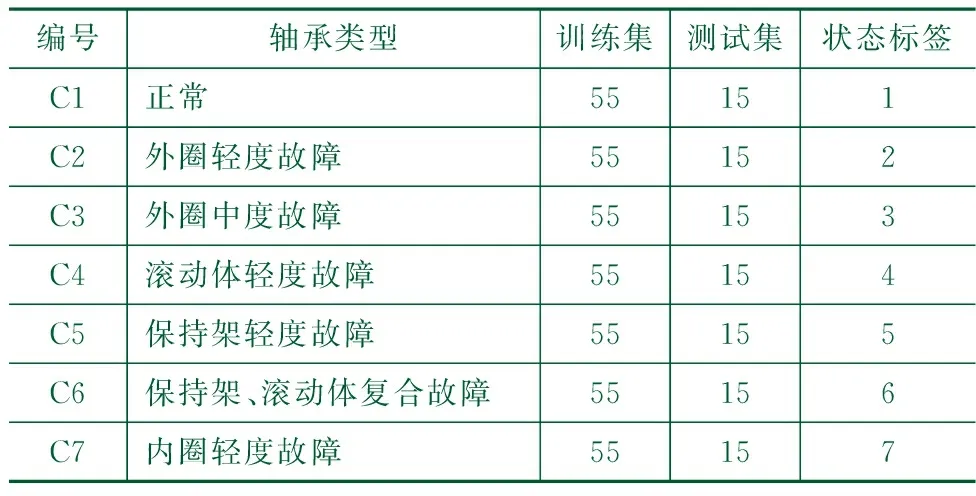
表1 故障类型及样本数量

4.2 信号的特征提取

试验采集的7种机车轴承数据均来自传感器B,单个样本信号包含2 401个数据点,共计490个样本。以轴承外圈中度故障为例,使用ICEEMDAN方法对样本信号分解,如图5所示。

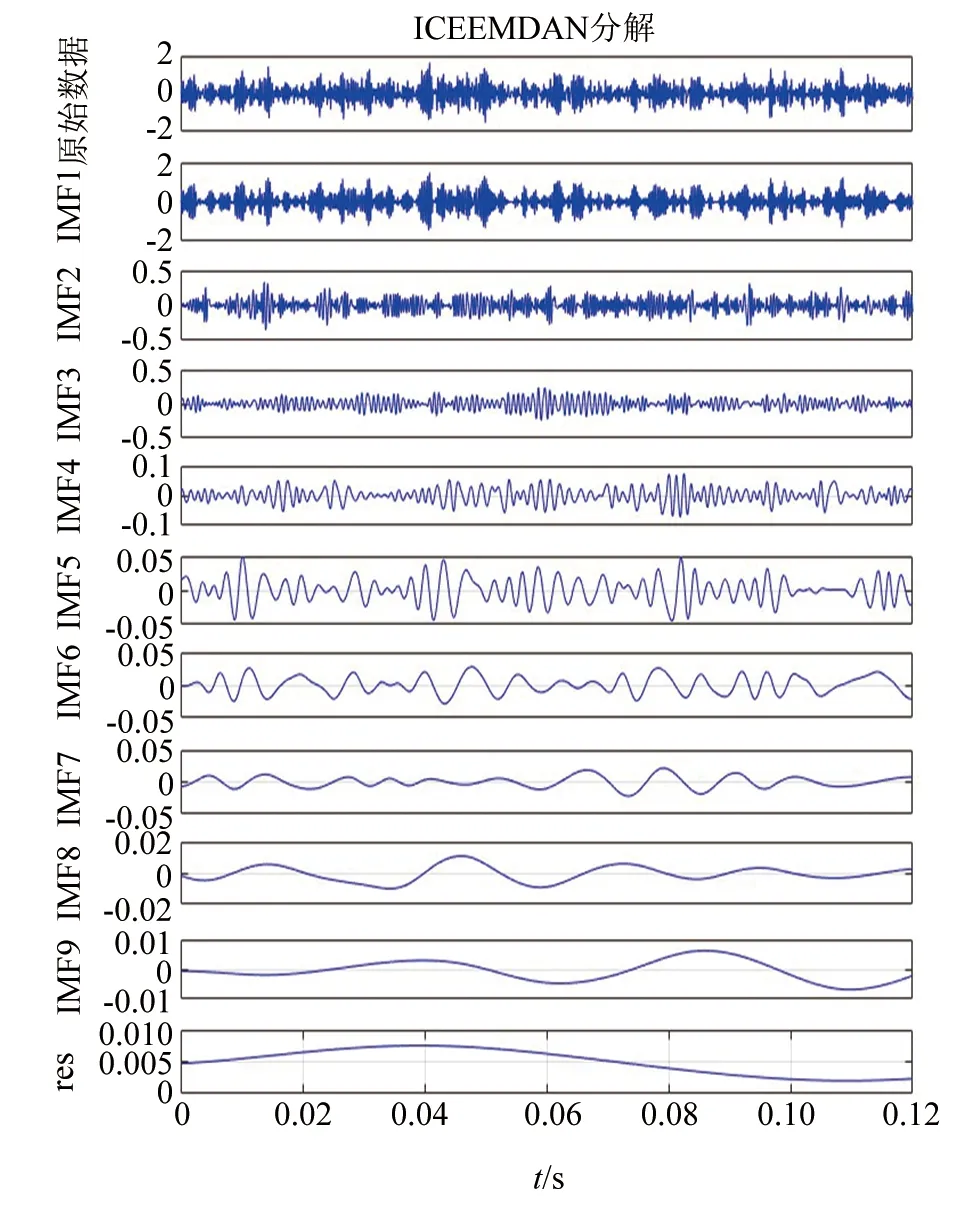
▲图5 轴承外圈中度故障ICEEMDAN分解结果

由图5可知,ICEEMDAN分解后产生了部分虚假分量,为剔除该部分虚假分量,本文引入相关系数准则,比较各分量与原始信号之间的相关性大小[12]。根据皮尔逊相关系数公式(式10)计算图5中各IMF分量与轴承外圈中度故障原始信号的相关系数,如图6所示:

(10)

由式(11)计算轴承不同状态下的相关系数阈值:

(11)

得到样本信号相关性阈值为μ=0.083 6,若ρxy>0.083 6,则将其对应IMF分量重构;若ρxy<0.083 6,则去除其相应分量。

由图6,选择ρxy>0.083 6对应的第1、2、3阶IMF作为特征分量进行重构。

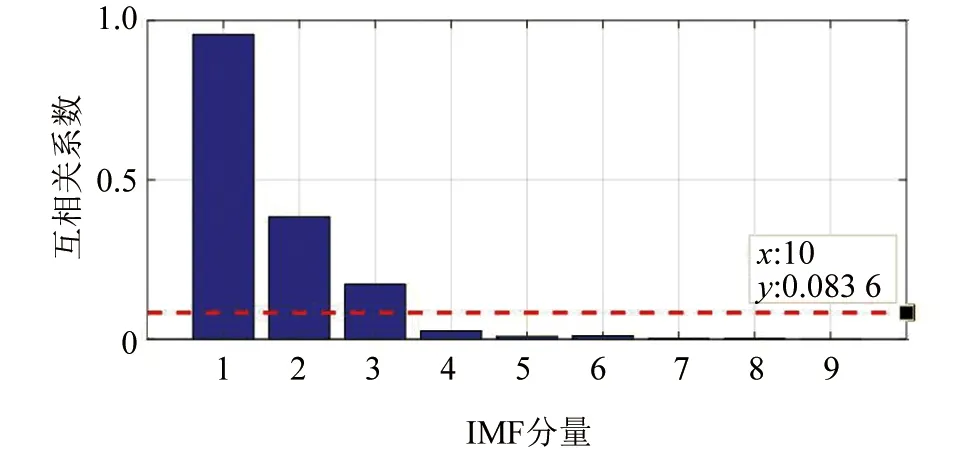
▲图6 ICEEMDAN分解后各IMF分量的互相关系数

对实验的滚动轴承7种状态下,每种状态70组数据分别做上述ICEEMDAN分解与阈值重构处理,得到各状态下的重构信号。图7为经ICEEMDAN分解后7种不同轴承健康状态的重构信号MSE值,可以看出它们熵值变化趋势大体相同,都随尺度因子的增加而降低,不同轴承重构信号的MSE值在前几个尺度上有重叠现象,但从第4个尺度后区分开始较为明显,交叉重叠现象减少。

为验证本文方法,设置对照实验,将相同的滚动轴承7种状态共490组样本进行CEEMDAN分解与阈值重构处理,得到各状态的对照组重构信号。

4.3 故障分类

设置GWO算法参数:P=20,N=100,优化参数数量为2,CV常数为5,设置c、g寻优范围为0.01-100。运行GWO算法,计算得到bestc=23.61,bestg=1.45。

分别对ICEEMDAN-MSE方法得到的特征向量与CEEMDAN-MSE方法得到的特征向量,使用未经优化的SVM分类模型进行识别,某次得到结果分别为图8(a)、图8(c)所示;使用相同的上述两组特征,应用经过GWO算法优化过的SVM分类模型进行分类,某次识别结果如图8(b)、图6(d)所示。滚动轴承7种状态的具体识别结果如表2所示。

表2 故障诊断结果

由表2可知,使用同一组前文设定的MSE参数求取特征向量时,当对信号进行CEEMDAN分解,且对SVM参数不进行算法优化,某次有31组样本被识别错误(如图8(a)所示),SVM的20次平均识别率为70.43%;在相同参数设置下,使用GWO算法对SVM超参数寻优后,分类平均识别率提高了22.95%,优化后SVM的20次平均识别率为93.38%。使用本文方法即对原始振动信号进行ICEEMDAN分解后,在MSE相同参数设置下进行故障状态识别,应用经GWO算法优化后的SVM分类模型,20次平均识别率为96.86%,较未优化SVM参数的模型20次平均识别率提高了23.57%,较CEEMDAN-MSE与GWO-SVM结合的方法总体识别率提高了3.48%,不同方法诊断准确率见图9。

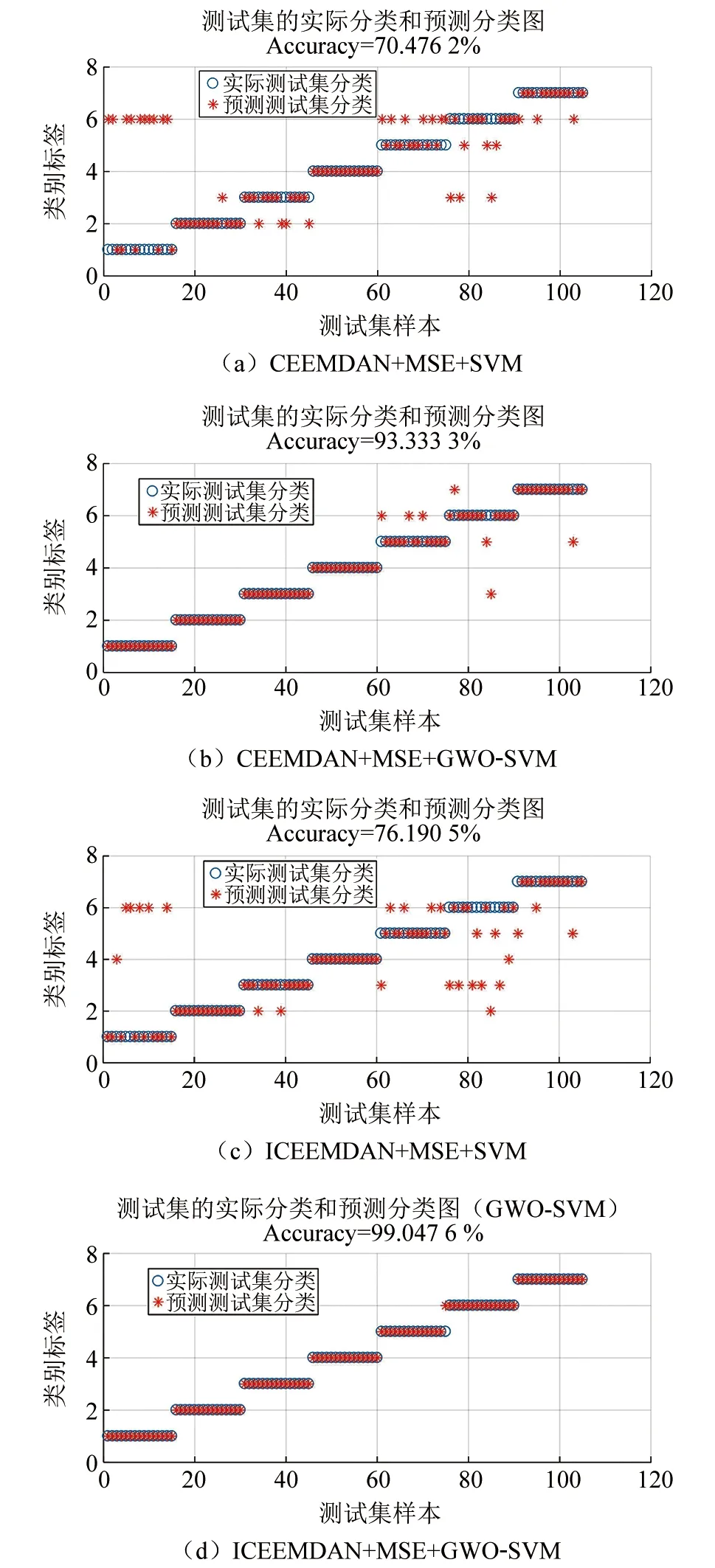
▲图8 识别结果比较

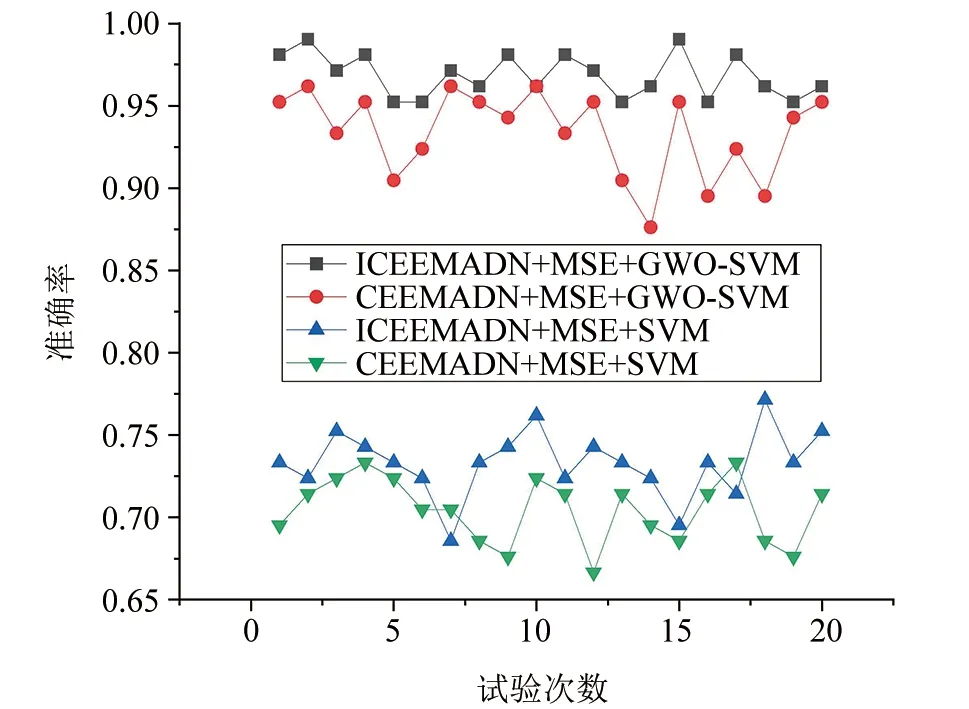
▲图9 不同方法诊断准确率

由图9可知,对真实机车轮对轴承振动信号使用ICEEMDAN分解,能有效改善CEEMDAN方法模态混叠、残余分量多等问题,在剔除掉与原始信号相关性小的部分分量后,重构信号故障特征较未处理前更明显,故准确率得到提高;使用同组设定的MSE参数得到的特征向量,GWO优化SVM超参数后进行识别时,进一步考虑了其核参数对分类结果的影响,使得所取惩罚因子c和核参数g更适应该特征矩阵,故使分类准确度获得大幅提升。由此表明本文方法在真实机车轮对轴承故障诊断场合下具有更加优越的性能。

5 结论

本文提出将ICEEMDAN、MSE方法与GWO-SVM模型结合,用于机车轮对轴承健康状态的分类,并应用真实的机车滚子轴承数据,验证了本方法的有效性和优越性。

(1) 使用ICEEMDAN方法分解原始信号,根据相关系数阈值法剔除相关性较小分量,并对保留的分量进行重构;

(2) MSE能有效表达真实机车轮对轴承振动信号的复杂特性;对SVM的超参数c、g进行灰狼算法全局寻优,避免了经验选参对识别结果的影响,有效提高了模型分类性能和自适应性;

(3) 本文所提方法得到各状态MSE值组成故障特征向量,经验证平均故障识别准确率为96.86%,与SVM参数未优化以及CEEMDAN分解的MSE值作为特征向量的GWO-SVM识别模型的结果进行对比,分别提高了23.57%、3.48%,且模型运行稳定,具备更好的鲁棒性,为机务段实际检测提供了一种有效方法。