基于MATLAB的H型钢切割机器人运动学分析与仿真

曾国祥, 刘志远, 李 进, 朱 珏*,

(1.宁波大学 压力容器与管道安全浙江省工程研究中心,浙江 宁波 315211,E-mail:zeng_guoxiang@163.com; 2.宁波大学 冲击与安全工程教育部重点实验室,浙江 宁波 315211)

工业机器人技术是第三次和第四次工业革命中非常重要的力量,它的发展对于国家制造业的发展起着举足轻重的作用[1]。从行业分布来看,工业机器人渗透率比较高的行业主要有:汽车制造业、电子和电气制造业、金属制品业和工业器械设备业等,而在劳动密集型的制造业中(如:家具制造业、纺织业、建筑工程业等),工业机器人渗透率是比较低的[2]。在建筑工程业中,对于H型钢需求日益增多[3],而目前对H型钢进行切割作业的自动化设备多为数控机床形式,采用工业机器人切割的设备则相对较少。例如:上海理工大学团队研发的基于RTEX总线型H型钢切割机,采用三割炬形式分别对两面翼缘和腹板进行切割[4];广东海洋大学团队研发的H型钢端头数控火焰切割机,采用数控编程方式解决需要切割的各种形式H型钢端头图形[5];天津大学团队研发的基于多机器人的H型钢数控切割机,设计了多机器人开放式数控切割系统[6]。这一类设备都是数控机床的形式,设备整体较为庞大,操作也较为复杂,主要在大型钢结构企业应用较多,在中小型企业仍以手动切割H型钢为主,辅以少量的半自动化切割机。因此本团队研究设计了一台基于机器视觉的H型钢切割机器人,能够通过视觉模块来采集待加工工件的尺寸信息并且生成工件的加工轮廓,再参考工件的端头轮廓要求得到机器人的加工轨迹,从而控制机器人来执行H型钢的切割任务。这种方式能够降低设备的操作难度,也能改善人工切割的质量、效率等问题。

而目前国内对于切割机器人的研究主要集中在控制系统的搭建和针对不同零件的切割工艺研究两方面,对机器人运动学分析等研究则更少些。华侨大学团队[7]研制了一种基于运动控制卡的切割机器人,控制系统采用的是PC和台达PCI-L221运动控制卡的方案,能够实现直接读取NC代码从而进行自动切割的功能;西华大学团队[8]研制的水切割机器人,控制系统以IPC为基础,PMAC运动控制器为核心,组成了主从分布式双微处理器的硬件控制方案,构建了一套开放式运动控制系统。哈尔滨理工大学团队[9]则根据管件相贯线数学模型和相贯线坡口的切割原理,建立了切割运动仿真模型从而得到了管件不同相贯形式的轨迹曲线。因此为了验证H型钢切割机器人设计的可行性,本文主要进行的是机器人的运动学分析与仿真研究,包括:(1)正运动学和逆运动学分析;(2)运用MATLAB建立机器人的运动学模型和工作空间模型;(3)仿真验证机器人的加工轨迹。机器人的运动学分析一方面是动力学分析的根基[10-12],另一方面也能够为工作空间、轨迹规划和运动控制等一些问题研究提供理论依据。

1 机器人系统组成设计

1.1 机器人机械结构设计

根据《切割机器人系统通用技术条件》[13],切割机器人按坐标形式可分为直角坐标型和旋转关节型。由于H型钢截面切割是空间立体作业,并且H型钢端头有多种类型,使得在实际工程中需要频繁变更切割轨迹,因此将切割机器人确定为直角坐标型,相比于旋转关节型切割机器人,它能在频繁变换切割轨迹的情况下还能保证操作的简便性;此外,在切割H型钢翼缘和腹板过程中切割枪需要变换姿态,并且翼缘有时需要切坡口,这就需要将切割枪旋转特定角度才能完成,如图1所示,因此设计了一种竖直偏摆和水平转动两自由度在机械结构上相互关联的旋转机构来完成这一要求。综上设计后确定了机器人的整体组成:X、Y、Z三维直角坐标结构+A、B二自由度旋转机构。

机器人的样机模型如图2所示,整机采取的是串联驱动结构,X、Y和Z三个直线移动轴由电机带动齿轮齿条机构沿着各自的导轨进行移动,A和B两个旋转轴由电机带动同步带机构实现切割枪的水平转动运动与竖直偏摆运动,从而实现切割枪姿态的变换。

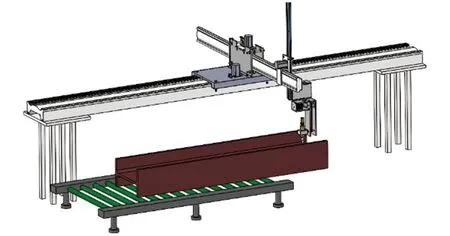
▲图2 机器人三维样机模型

1.2 机器人控制系统设计

控制系统主要包含工业相机、上位机和下位机三个部分。工业相机用来对H型钢端面进行图像采集;上位机是在PC端的软件部分,包含:图像处理模块、轨迹计算模块、运动控制模块和通讯模块,主要功能是对数据进行采集、处理和发送以及通过界面进行操作人员与机器人的交互;下位机是PLC控制模块和电路硬件模块,主要功能是执行上位机发送过来的指令以及对机器人的各关节电机和其它外接设备发送相关动作指令。机器人控制系统总体方案设计如图3。

2 机器人运动学分析

已知机器人各关节运动学参数,解出末端执行器运动学参数即是工业机器人正运动学,反之即是工业机器人逆运动学[14]。

2.1 建立机器人数学模型

确切的描述出机器人姿态与位置是进行机器人运动学分析的基础。本文采取标准D-H参数法[15]进行机器人运动学分析,首先根据切割机器人的三维设计模型求出机器人的D-H参数(表1),然后简化机器人的本体模型,并且绘出空间直角坐标串联型切割机器人的D-H坐标系机构简图(图4),再根据D-H参数求得关节变换矩阵。

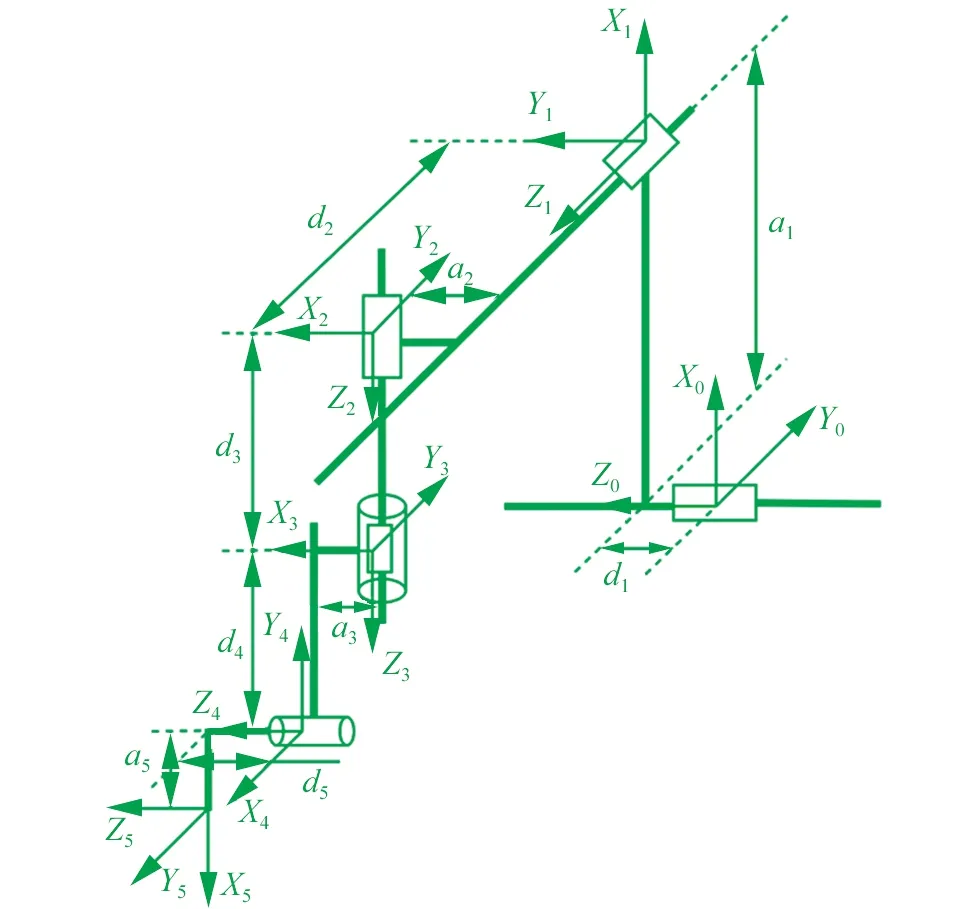
▲图4 机器人D-H坐标简图

表1中,θn表示Xn-1轴与Xn轴之间的夹角;dn表示n-1系沿Zn-1轴正方向的距离;an表示n-1系沿Xn轴正方向的距离;αn表示Zn-1轴与Zn轴之间的夹角。

2.2 机器人正运动学分析

建立了各个连杆的坐标系之后,n-1系和n系之间的关系就可以用坐标系的平移和旋转来实现:首先令n-1系绕Zn-1轴旋转θn,再沿Zn-1轴平移dn,然后沿Xn轴平移an,最后绕Xn轴旋转αn,使n-1系与n系重合。用一个齐次变换矩阵An来表示上述的四次变换[16],即An表示第n连杆坐标系相对于第n-1连杆坐标系的齐次变换,为:

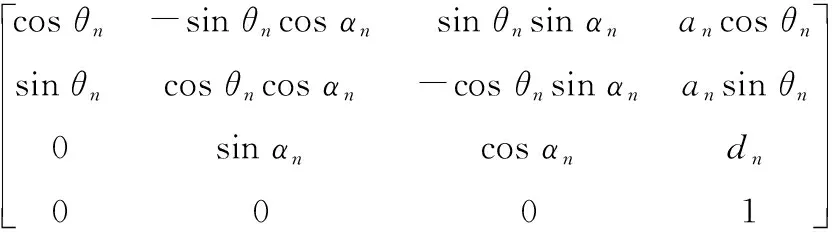
(1)

则第一连杆坐标系相对于基坐标系的位姿T1为:

T1=A1T0=A1

(2)

T0表示基坐标系的位姿矩阵,即:

第二连杆坐标系相对于第一坐标系的位姿T2为:

T2=A1A2

(3)

通过推算,机器人末端执行器坐标系相对于基坐标系的位姿T5为:

(4)

将表1数据代入式(1)中求出齐次变换矩阵A1、A2、A3、A4、A5,再将A1～A5代入式(4)中可得出机器人的末端执行器位姿矩阵为:

(5)

2.3 机器人逆运动学分析

在上文正运动学的分析中得出了末端执行器的位姿矩阵T5,若给定具体的该位姿矩阵各参数则可以求得机器人的各个关节变量:d1、d2、d3、θ4和θ5。其中,θ4表示水平转动关节A的关节变量,它的作用是确定需要切割翼缘坡口时的切割角度;θ5表示竖直偏摆关节B的关节变量,它的作用是对火焰切割枪进行切割翼缘和腹板两种不同姿态的变换以及确保在切割腹板时切割枪能对腹板边缘圆角处进行切割。

▲图5 A、B关节转动示意图

因此可以通过末端火焰切割枪的姿态推算出两关节变量θ4和θ5。假设翼缘坡口角度为m,切割腹板圆角处切割枪旋转角度为n,如图5所示,则:

θ4=-m

θ5=n

得出θ4和θ5之后,代入式 (5)中,可分别解出d1、d2和d3,即:

d1=pz-145+50sinm-113cosmcosn

d2=py+50cosm+113sinmcosn

d3=-px-55.4-113sinn

3 机器人MATLAB运动学仿真

3.1 建立机器人运动仿真模型

结合第2节中正运动学和逆运动学的分析,再通过MATLAB中Robotics Toolbox工具箱的Serial Link和Link函数,建立切割机器人的运动学仿真模型(图6)。利用该模型,可以对正逆运动学理论的分析进行验证以及进行机器人轨迹控制算法的设计。

3.2 机器人工作空间仿真

由于H型钢切割机器人的加工作业对工作空间有特定的要求,所以需要对机器人的工作空间实行仿真,从而确定所需切割作业的工件尺寸范围。将本文机器人的工作空间表示为S(P),则各关节变量与工作空间的关系可用下式来表示:

S(P)={P(d,θ):d∈M,θ∈N}

(6)

式中:d=[d1,d2,d3],θ=[θ4,θ5]为关节变量。

M和N为约束空间,应该结合实际情况进行确定:

M={d|di-min≤di≤di-max,i=1,2,3}

N={θ|θj-min≤θj≤θj-max,j=4,5}

di-max/θj-max与di-min/θj-min分别为关节(移动/旋转)运动的上限与下限,因此机器人的工作空间可以表示为:

(7)

本文采用Monte Carlo随机数算法[17]来求解机器人末端执行器工作空间。此算法是一种运用随机概率来求解问题的数值方法,能够把运动空间近似数字化,经常用在机器人的工作空间求解问题中[18]。在MATLAB当中,运用函数rand(),随机生成各关节变量:d1、d2、d3、θ4和θ5在各自定义区间内的数值,即:di=di-min+(di-max-di-min)·rand(1),i=1,2,3;θj=θj-min+(θj-max-θj-min)·rand(1),j=4,5。机器人各关节范围参数为:d1∈[0,1 500],d2∈[0,1 200],d3∈[0,700],θ4∈[-90°,90°],θ5∈[-90°,90°];各连杆参数:a1=170 mm,a2=30 mm,a3=115 mm,a5=113 mm,d4=225.4 mm,d5=50 mm。将这些参数代入到机器人末端执行器的位置方程当中,得出机器人末端执行器工作空间,如图7所示。

▲图7 机器人末端执行器工作空间仿真图

3.3 机器人轨迹规划分析

轨迹规划的主要目标是为运动控制系统生成预期输入,来保证机器人按照预定的轨迹执行运动[19]。本文设计的切割机器人虽然是在三维立体空间对H型钢进行端头切割,但H型钢的翼缘及腹板皆为平面板材,所以不需要分析三维运动学轨迹,切割轨迹可分解为各平面上的二维轨迹,如图8所示,在采集H型钢截面尺寸参数后基本可以由轨迹点集来进行二维量化,机器人的轨迹插值方式采取五次多项式插值法进行二维插值计算。

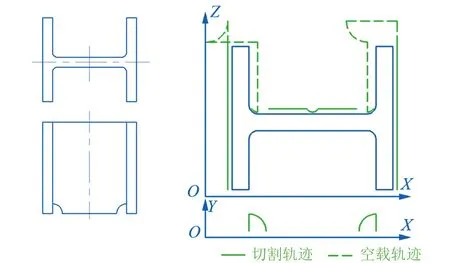
▲图8 某一切割轨迹的二维分解

针对不同端头类型的H型钢,需要设计不同的切割加工轨迹。在加工过程当中,为了确保H型钢的端面切割能获得较好的效果,需要确保机器人的各个移动关节电机和旋转关节电机有一定的运动精度与稳定性。所以切割路径点集的选择就会决定末端执行器的加工轨迹设计是否相对合理。H型钢切割机器人末端执行器的加工轨迹是以机器视觉模块采集处理的H型钢截面尺寸信息及输入的端头类型相关切割参数进行规划与执行的。

对机器人进行轨迹规划的方法主要有:在关节空间中规划和在笛卡尔空间中规划[20-21]。在关节空间中进行轨迹规划时的计算量比较小,而且不会出现奇异问题,但机器人的末端执行器在工作空间中的运动轨迹是未知的;在笛卡尔空间中进行轨迹规划,机器人运动路径直观清晰,但不能判断机器人在运动过程中是否会出现奇异问题[22]。因为对H型钢端面切割所需规划的轨迹是直线型或圆弧型,求逆解的运算量比对各关节分析规划的运算量小,并且末端执行器的五次插值计算更为简易,使得仿真能够达到较好的效果,所以本文在笛卡尔空间中实行轨迹规划,运用MATLAB中的ctraj函数对机器人的加工轨迹进行运动学仿真。

3.4 机器人轨迹规划仿真

设需要切割的工件尺寸为400 mm×355 mm×20 mm×200 mm,如图9(b)所示。根据机器人机架和零件的相对位置,设定切割枪的初始加工位置,并且设定零件的切割轨迹路径点集:q1=[0,0,0];q2=[0,0,400];q3=[0,0,520];q5=[0,198,520];q6=[0,198,210];q8=[50,198,210];q9=[0,248,210];q10=[0,298,210];q12=[0,348,210];q13=[50,398,520];q14=[0,398,210];q16=[0,398,520];q18=[0,483,520];q19=[0,483,400];q20=[0,483,0]。根据路径点集可进行切割轨迹的规划,如图9(c)所示。

轨迹规划完成之后,再编写MATLAB程序,设置相应的步长和时间参数执行仿真。机器人末端执行器的切割加工轨迹仿真如图10所示。因而通过仿真实验判断,所选取的轨迹路径点集相对合理,验证了上文运动切割轨迹规划的合理性。

▲图9 某一切割轨迹示意图

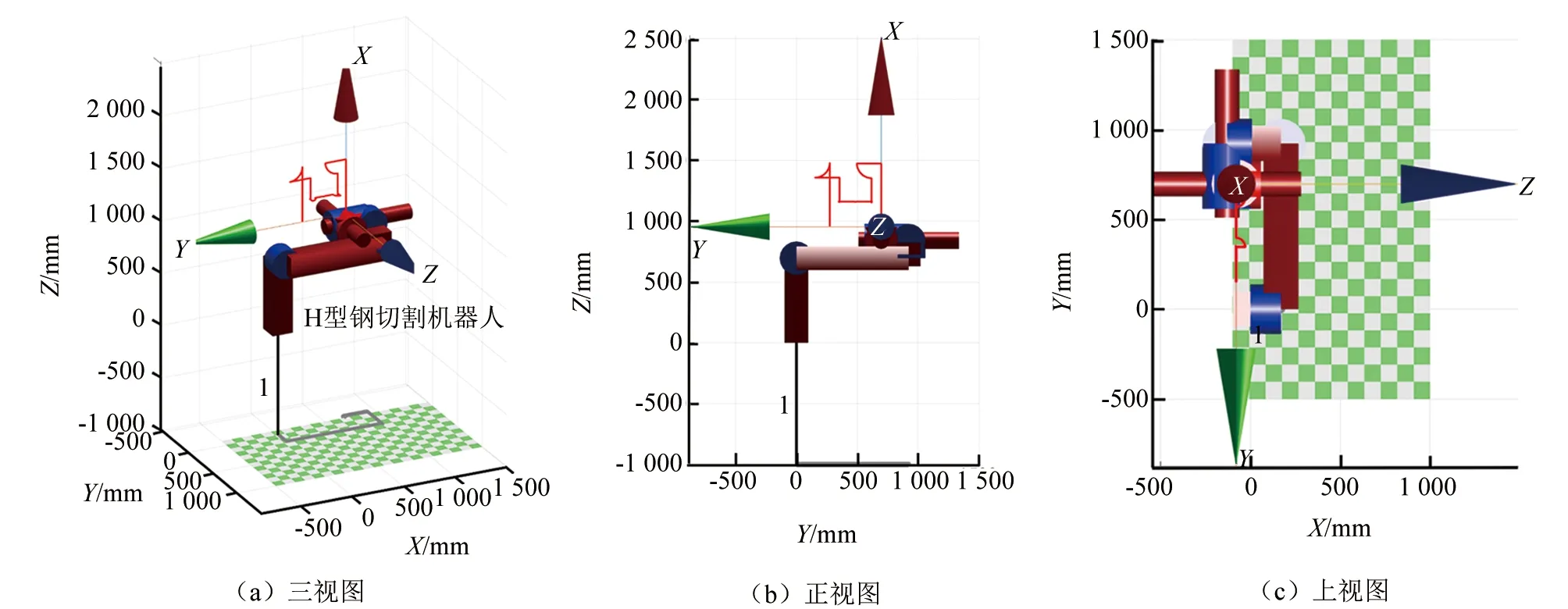
▲图10 机器人切割枪末端轨迹仿真图

4 样机实验测试

根据第1节中对于机器人的系统组成设计,所制作的H型钢切割机器人物理样机如图11所示。

▲图11 H型钢切割机器人物理样机

▲图12 测试切割效果

通过该样机对H型钢进行切割测试,即先通过机器视觉部分分析H型钢的尺寸参数,同时结合所需切割端头类型自动规划出切割轨迹,从而进行切割。所测试效果如图12,与人工手动切割效果对比,所设计的H型钢切割机器人能有效改善人工切割所存在的质量及效率问题。

5 结论

本文依据实际工作情况的切割作业需求实行了机器人的机械结构设计和控制系统设计;根据机械结构模型使用标准D-H参数法创建了机器人的D-H坐标系,推算了机器人正运动学与逆运动学的数学模型;运用MATLAB建立了机器人的仿真模型,对机器人模型是否能够满足H型钢端头切割的要求进行了验证;利用Monte Carlo随机数算法得出了机器人的工作空间;利用五次多项式插值算法,实现了末端执行器的轨迹规划与仿真。

通过仿真实验,验证了机器人设计的有效性,为机器人的实际加工轨迹规划建立了理论依据,也为机器人控制算法研究和动力学仿真确立了基础;通过样机测试实验,证明了机器人实际切割作业的可行性。