优化变分模态分解的超声多普勒测流信号误差模型研究
2023-09-16赵军华戴聪聪张清波
赵军华,戴聪聪,李 丛,冯 阳,邓 权,张清波
(深圳市宏电技术股份有限公司,感知研发中心,广东 深圳 518000)
0 引 言
近年来,随着科技的飞速发展,农田灌溉、水流监测、家用水表、工厂用水监测等不同领域都广泛使用了超声多普勒流量计,其测量精度和误差也直接影响产品的工作效率[1]。在实际应用环境中,由于液体密度的不均匀性,发射的超声波产生折射和衍射现象,导致回波信号中会夹杂着各类不同的噪声干扰,尤其是受白天阳光影响直接导致信号完全被噪声淹没[2],因此测量液体流量的超声回波信号大多是低信噪比、非线性、非平稳信号[3,4]。如何提取回波信号中的有效信号成为实现超声流量计高精度、高可靠性的关键。目前常用的去噪方法主要有小波阈值去噪[5,6]、经验模态分解(EMD)[7,8],从多尺度将信号分解成不同频率的分量、具有良好时频局部化特性的小波阈值去噪由于小波基的选取问题,不具备自适应分解能力,虽然EMD 通过添加白噪声解决了小波阈值去噪自适应问题,能自适应分解多个本征模态函数分量(IMF),但仍存在模态混合、缺乏严格的理论公式、算法效率低、抗噪性能差等诸多问题。因此,EMD 并不能精确地分离出有用信号[9]。
2014 年,Xie[10]提出了一种新的时频分析法—变分模态分解(VMD),该方法以强大的数学基础来解析信号瞬时频率,具有实际的物理意义,通过迭代搜索模型最优解来实现信号精准分离的同时利用自身的Wiener 滤波特性可以获得不错的去噪效果,克服了EMD 的模态混叠问题,所以VMD 也被广泛使用在非平稳信号处理中[11-13]。然而,VMD 算法受其惩罚因子和分解层数参数影响,设置不当极易导致过分解问题,还需进一步优化[14,15]。海鸥算法(SOA)具有较强的全局搜索能力,它可以适用于参数寻优[16],相对于其他优化算法如麻雀、蝙蝠等具有较强的鲁棒性,但海鸥算法在更新种群位置时极易被束缚,导致在后续迭代过程中陷入局部最优,造成结果的多样性[17,18]。
因此利用海鸥算法结合VMD 对超声多普勒信号进行降噪处理,引入柯西变异算子(CV),设置随机扰动解决海鸥算法迭代过程中陷入局部最优的问题,优化VMD 参数以包络谱值为自适应度函数,将云相似度计算作为有效分量筛选标准。并针对VMD 出现的中低频振荡现象引入奇异频谱分析(SSA),进一步提高回波信号信噪比。
1 算法原理
1.1 VMD原理
VMD 算法可将任何信号从低频到高频进行有效分离。在这个算法中,各模态分量及其对应中心频率的确定是一个约束问题,可引入二次惩罚因子和拉格朗日乘数,使问题不受约束,在频域内不断更新模态分量、中心频率和拉格朗日乘数,直到获得变分约束问题的最优解为止。
1.2 CVSOA优化VMD参数
海鸥算法因具有超强的全局搜索能力和易于操作实现的特点,使得它可适用于参数寻优。其基本原理是计算“海鸥的最佳运动位置”作为问题解,算法主要有两种行为:
(1)迁徙行为。海鸥个体更新探索新位置,个体之间避免碰撞且与最优个体保持密切联系。
式中:Cs表示海鸥种群所有个体相互分散的位置;Ps表示单个海鸥所处位置;x表示当前迭代次数;A表示在一定空间内海鸥的迁徙行为;fc表示常数可调整海鸥位置。
更新完海鸥位置后,海鸥个体保证不会碰撞且会根据最优海鸥个体方向移动。
式中:Ms表示海鸥个体所处位置Ps向记录的当前最优值位置Pbs移动路径;B的取值是随机的,它可以适当地平衡搜索和扩展行为;rd为一个随机数,范围为[0,1]。
同时,海鸥个体根据收敛方向向新位置进行移动。
式中:Ds表示海鸥个体新位置。
(2)攻击行为。海鸥进攻行为呈螺旋形下降。其行为轨迹x轴、y轴、z轴分量分别如下式所示。
式中:Ps(x)为存储历史最佳海鸥位置,位置更新时,算子易被Pbs束缚,易被固定在某个区域,从而影响了结果的多样性,即陷入局部最优。
通常情况下,设置随机可解决这个问题。Cauchy 分布的随机序列两翼分布较宽,零点波峰高于Guassian 分布,比Guassian分布的抗干扰能力更强。
则可利用柯西变异来改进SOA算法。计算公式为:
式中:Cauchy(0,1)为分布函数;rand(0,1)是一个均匀分布随机数;p为随机变异概率。
在迭代后期,进入收敛状态所有海鸥个体攻击到同一位置不再更新。因此,结合柯西变异策略,对其更新的位置设置扰动,逃离早熟状态。实现步骤如下:
(1)陷入局部最优后,判断随机数是否小于变异概率p。
(2)对最佳海鸥个体位置Pbs进行柯西变异,并保留Pbs。
(3)判断海鸥种群是否继续陷入局部最优,若是,则循环步骤(1)~(3),否则找到全局最优。
利用下式对Pbs进行变异策略。
式中:rand 为一个大于0且小于1的均匀分布随机数;Pbs为当前海鸥种群最佳个体位置。
1.3 CVSOA-VMD适应度函数
根据CVSOA 算法理念,需要依据适应度函数来评判参数组合是否为最优结果。文献[19]提出了包络熵的概念,包络熵可以更好地反映信号的稀疏特性和不确定程度,数值越大,信号的不确定性也就越大。本文选用包络熵作为CVSOA 的适应度函数,x(j)(j= 1,2,…,N)信号计算公式如下:
式中:N为信号采样点数;a(j)为信号x(j)经Hilbert解调后得到的包络信号。
1.4 融合VMD与SSA的降噪模型
云相似度法是基于云模型理论提出的一种衡量两向量的相似方法。将CVSOA 用于VMD 参数优化,以包络谱熵值作为CVSOA 的适应度函数,将信号按最优参数进行VMD 分解,得到一系列IMFs,计算其云相似度值,将阈值以下判定为杂波分量并去除,最后利用SSA 去除残余噪声。具体步骤流程如图1所示。

图1 融合VMD与SSA的降噪算法流程图Fig.1 Flow chart of noise reduction algorithm integrating VMD and SSA
(1)通过逆向云发生器[20]得到原始信号y(t)的云向量=(Ex,En,He)。
(2)通过CVSOA-VMD 分解原始回波信号y(t),得到IMFk(k= 1,2…,n)。
(4)求取原始信号与各云向量的余弦夹角作为云相似度值,即:
(5)采用统计分析法确定阈值大小,将低于阈值的IMF分量去除,得到有效IMF分量。
(6)对有效分量进行重构,进行SSA 二次谐波处理后得到最终去噪信号。
2 算例分析
为了验证该方法的可行性和有效性,分别采用以下3种方案处理模拟信号和实测走车数据。方案一:通过EMD 分解信号得到IMF 组分,利用云相似度对各组分进行相关性分析,重构有效组分,进行SSA 二次滤波处理;方案二:利用SOA对VMD 参数进行优化,按最优参数分解得到IMF 成分,并将干扰成分筛选掉重构有效成分,进行SSA 二次滤波处理;方案三:利用CV 对SOA 进行优化,根据最优参数分解得到的IMF分量,计算云相似值筛选出噪声分量,再对重构信号进行SSA二次滤波,得到最终的降噪信号。便于表述和分析,方案一、二、三分别记为EMD-SSA、SOA-VMD-SSA 和CVSOAVMD-SSA。
2.1 仿真信号分析
由于实测数据中含有一定的误差,因此方法的有效性和可行性首先通过模拟信号进行验证。根据超声波时间序列的特点,根据公式(11)生成模拟信号[21],时间为2 ms,频率为500 kHz,加入高斯白噪声,其信噪比为8,其含噪波形如图2所示。
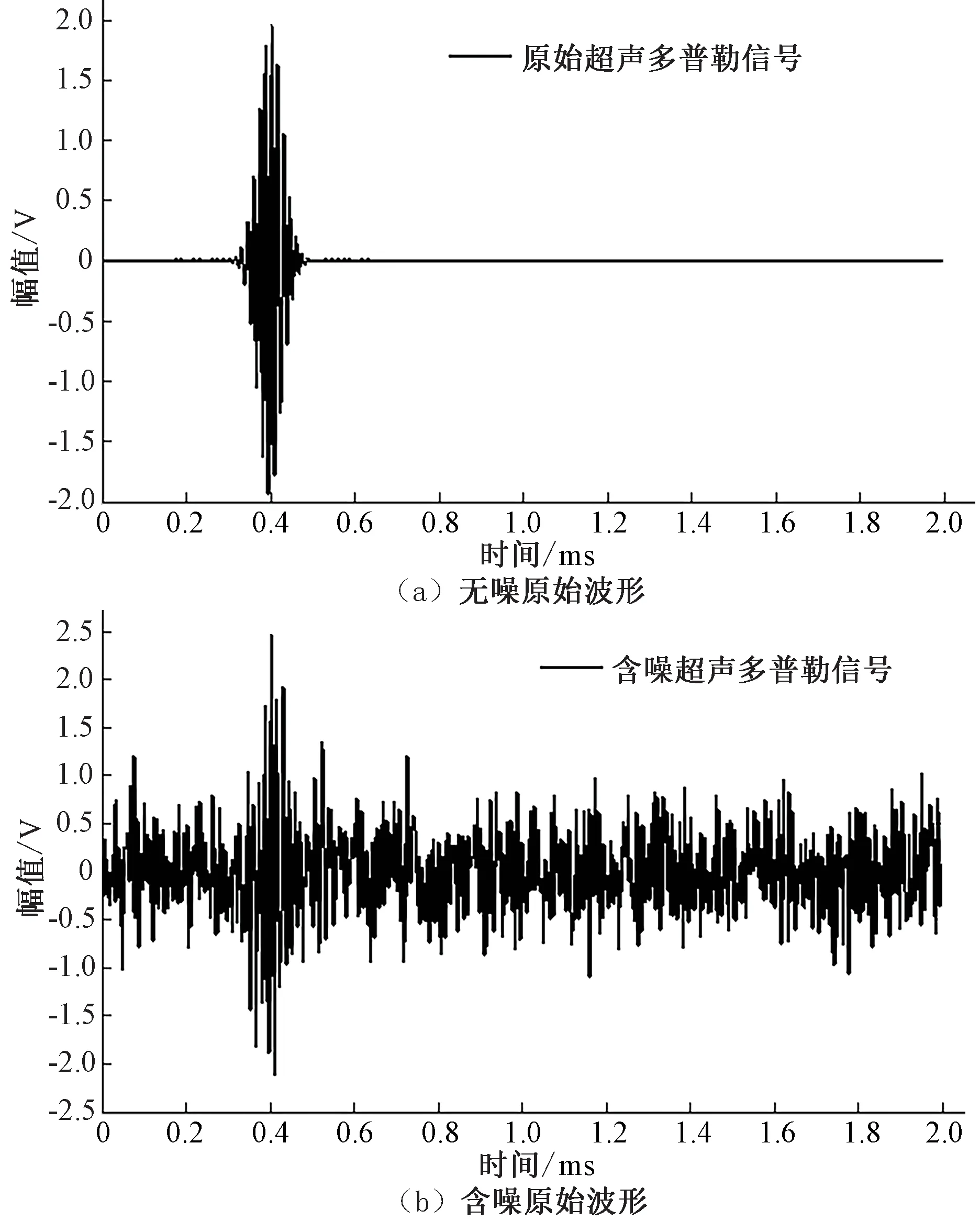
图2 时域波形图Fig.2 Time domain waveform
式中:A、a、f、τ分别为信号的幅值、衰减系数、特征频率和峰值时刻。
采用VMD 对含噪仿真信号进行分析,选取包络谱熵值作为CVSOA 的适应度函数,利用CVSOA 对惩罚因子α和模态分解个数K值进行寻优。考虑到分解层数K设置过大而引起的过分解现象,设定K值运算最大值为9。图3 是海鸥种群进化迭代变化的对比曲线图,图3 中为两种方法的全局最优包络谱值。
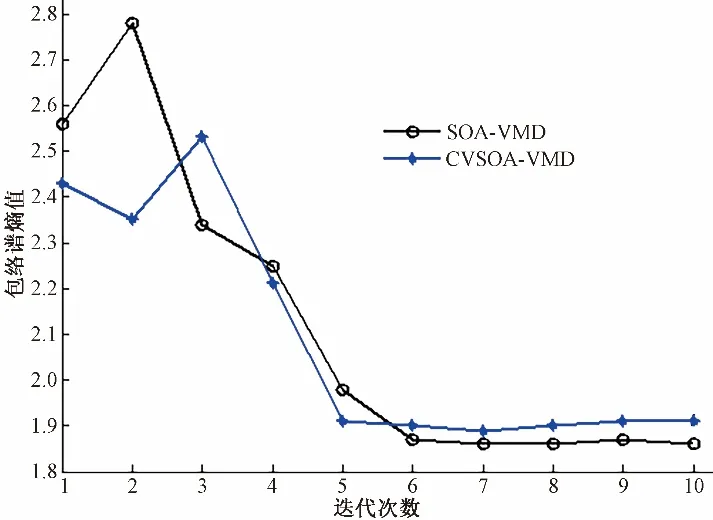
图3 迭代次数与包络谱熵值关系图Fig.3 Relation between iteration times and envelope spectrum entropy
由图3 可以看出:CVSOA 算法优化VMD 在第5 次迭代收敛,包络谱熵值为1.942,最佳参数组合为[4 365,6],SOA算法优化VMD 在第6 次迭代收敛,包络谱熵值为1.913,最佳参数组合为[8 327,6],分别利用最优参数对仿真信号进行VMD 分解,如图4所示。
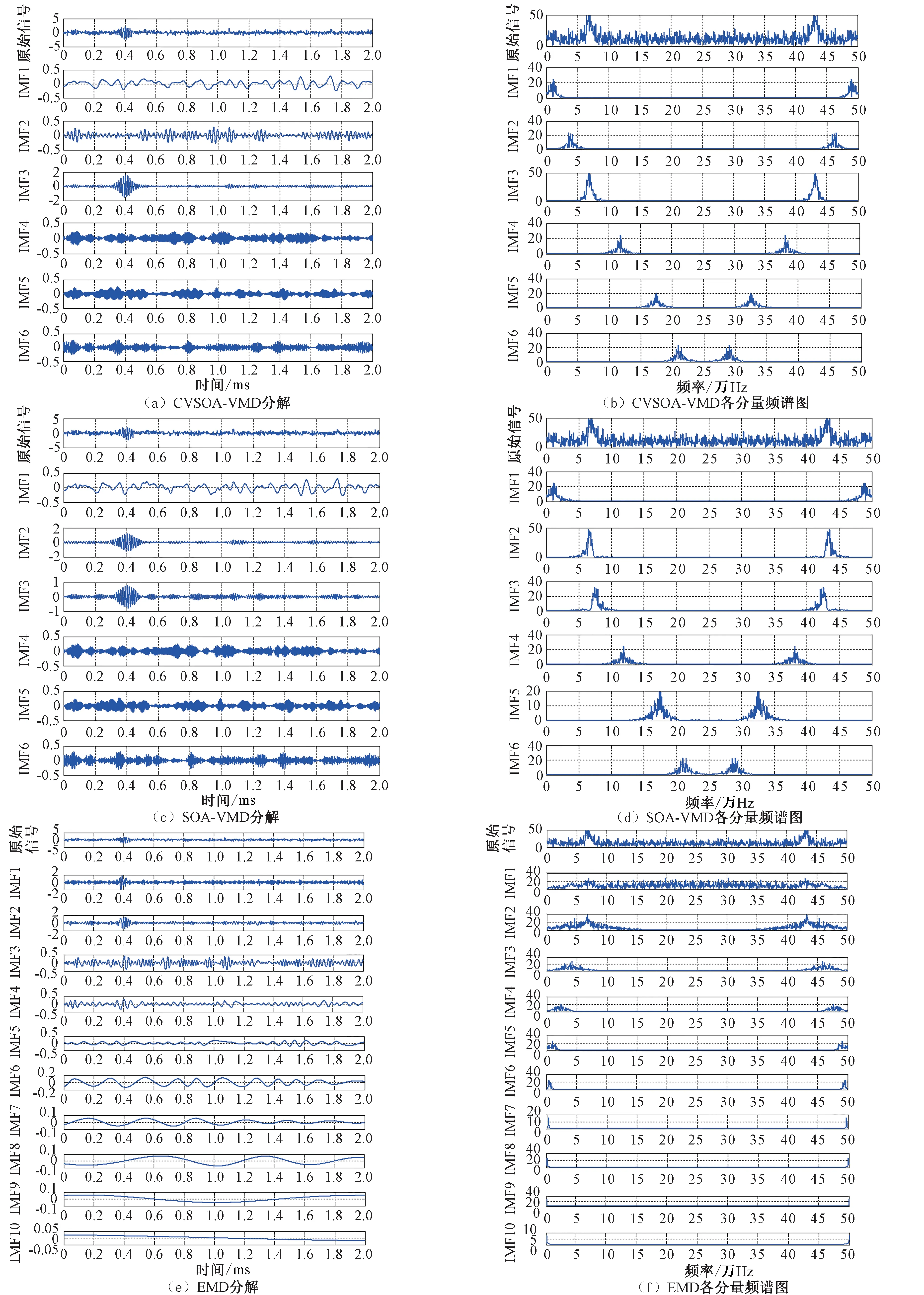
图4 EMD、VMD模拟信号分量图Fig.4 EMD and VMD analog signal component diagrams
从图4 中的对比分析可以看出:VMD 分解模态从低频到高频分布,低频振荡也主要集中在前几阶模态中。EMD 分解模态从高频到低频排列,信号能量主要集中在高阶模态中,多个分量出现严重的模态混叠现象,分解出多个原本属于同一分量部分信息的低频分量,这是由于EMD 终止条件的不合理,导致了过分解;SOA-VMD 分解的IMF2、IMF3 分量产生频率重叠部分。相比之下,CVSOA-VMD 分解的各分量频率单一,模态混叠现象的抑制效果更好,优于EMD 和SOAVMD 方法。以求准确筛选信号和噪声分量,分别计算各分量的云相似度值,图5 为3 种分解算法各分量云相似度值,图5中3种方法都取IMF1~IMF6分量。
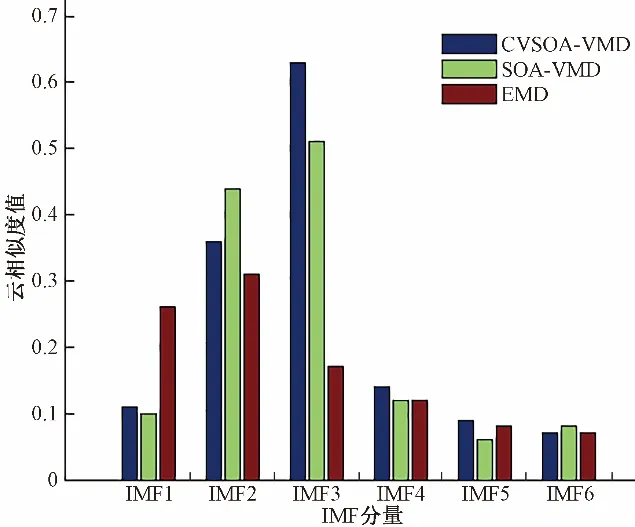
图5 3种分解算法各分量云相似度值Fig.5 Cloud similarity values of each component of three decomposition Algorithms
由图5分析可知:阶数分量靠前的云相似度值更大,云相似度值越大的分量与原始信号波形相似度也越大,可以看出CVSOA-VMD 分解的IMF3分量与无噪原始信号最接近,SOAVMD 分解的IMF2、IMF3 分量与无噪原始信号最接近。3 种分解算法云相似度值都呈现先增大后减小的趋势,将IMF 分量小于阈值0.4 视为噪声成分。对有效成分进行重构,采用SSA进行二次谐波降噪处理,上述3种方案降噪处理后的结果如图6所示。

图6 3种算法降噪信号图Fig.6 Three algorithms for denoising signals
对比图6可以看出:CVSOA-VMD-SSA 有效抑制了谐波干扰,幅值及趋势变化得到了完整地保留,相比EMD-SSA、SOA-VMD-SSA 更平滑,与无噪原始信号存在差异最小,变化规律趋势也更接近。加入不同信噪比的白噪声,以均方根误差和信噪比等两个指标进行评价,定量分析和说明上述3种方案对模拟信号的降噪效果,计算结果如图7所示。
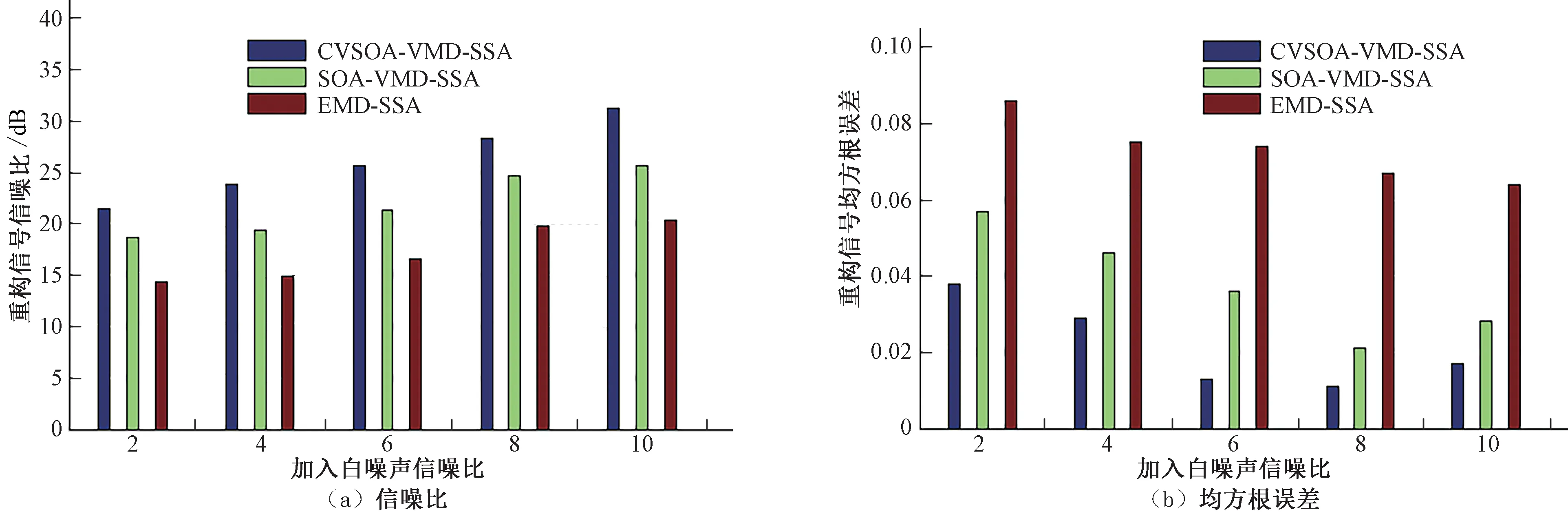
图7 信噪比及均方根误差Fig.7 The signal-to-noise ratio and root mean square error
由图7可知:随着白噪声信噪比的增加,去噪信号的信噪比逐渐增大,均方根误差逐渐减小,CVSOA-VMD-SSA 较SOA-VMD-SSA、EMD-SSA 均有改善,信噪比可达30.78 dB,均方根误差最低达到0.01,说明与原信号的差异最小,去噪效果更好,更能反映原信号的特征信息。
3 走车实验分析
3.1 水槽走车实验
水槽走车试验是以水槽中的水保持静止、走车带动流速仪在水槽中以设定的匀速运动为原则设计的,实验装置如图8 所示。走车速度可通过PLC 上位机操作设定在全范围内的任意恒定速度值,走车装置最大额定速度可达3 m/s,水槽长度为30 m,宽度为1 m,深度为1.2 m。此次走车实验速度设置为0.3 m/s,走车距离为30 m,流量计紧扣固定在走车装置上,将流量计的外接线通过485 转232 串口连接到电脑上,串口助手进行数据接收。首先对串口接收的数据进行去趋势分析,图9 为走车实测的超声回波时域波形图。

图8 实验装置图Fig.8 Experimental device

图9 实测原始信号Fig.9 Original signal
3.2 信号降噪处理
接下来对图9 采样的时域信号利用CVSOA 对VMD 参数进行寻优,最优参数组合分别为[3 894,6]、[7 652,6],按最优参数组合对信号进行VMD 分解,计算各分量的云相似度值,结果如表1所示。

表1 不同分量云相似度值Tab.1 Cloud similarity values of different components
从表1 中可以看出,IMF1~IMF5 分量的相似度值差异明显,差值范围在0.32~0.52 左右。为进一步观察云相似度值的分布规律和门槛选择的可靠性及普遍性,取超声多普勒信号10 组,分别进行CVSOA-VMD 分解,再计算云相似度值,限于篇幅取前5 组。如表2 所示,是每组信号的最优参数组合。

表2 各样本最优参数组合Tab.2 Optimal parameter combination of each sample
由表2 可知,第6 组信号分解模态个数为5,故曲线拟合均取前5个分量的云相似度值,如图10所示。
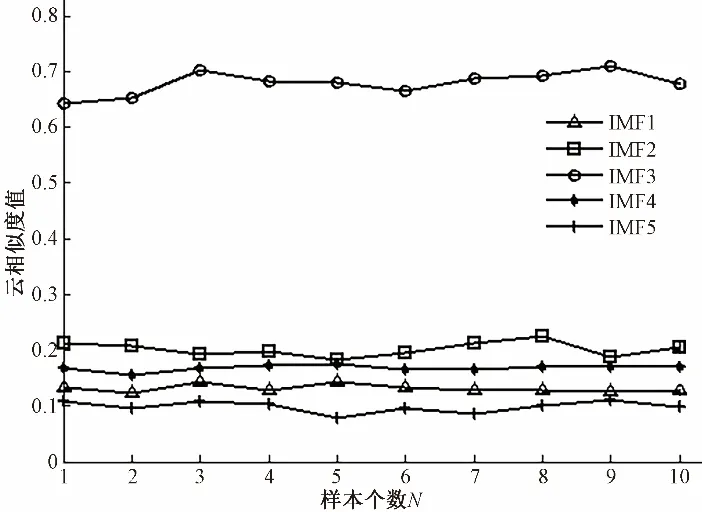
图10 云相似度值拟合曲线图Fig.10 Cloud similarity value fitting curve
由图10 可知:IMF3 成分虽有一定波动,但各值均较大,说明与原信号最有关联,含原始信息量最多,能完全反映原信号的特征信息,而IMF1、IMF2、IMF4、IMF5 的云相似度值均较低,表明与原始信号没有关联。根据多次实验统计分析确定云相似度阈值为0.6。因此,选择以上包含最多原始信号特征的IMF成分进行重构,并对重构信号进行SSA二次谐波干扰抑制,如图11所示,得到最终降噪信号。
通过对比图11(a)、图11(b)分析可知,直接小波阈值去噪信号更光滑,但是信号出现失真较为严重,EMD-SSA 去噪不彻底,还残留少部分噪声,而图11(c)、图11(d)基本去除了存在的噪声,但SOA-VMD-SSA 去噪波峰波谷值不能很好保留,相比之下CVSOA-VMD-SSA 能够很好的保留波峰波谷值且噪声抑制效果更好。计算其信噪比和均方根误差,以进一步量化CVSOA-VMD-SSA 算法的去噪效果,结果如表3所示。
由表3 分析可知,CVSOA-VMD-SSA 信噪比达21.71 dB,相比直接小波阈值、EMD-SSA、SOA-VMD-SSA 分别提高13.35、8.90、5.47 dB;均方根误差最低达0.010 4,表明CVSOA-VMD-SSA 方法的去噪效果更优。为更进一步验证去噪算法对流速探测精度的影响,表4给出了文中所述的几种算法在探测流速在0.1~0.6 m/s范围内的测速误差。
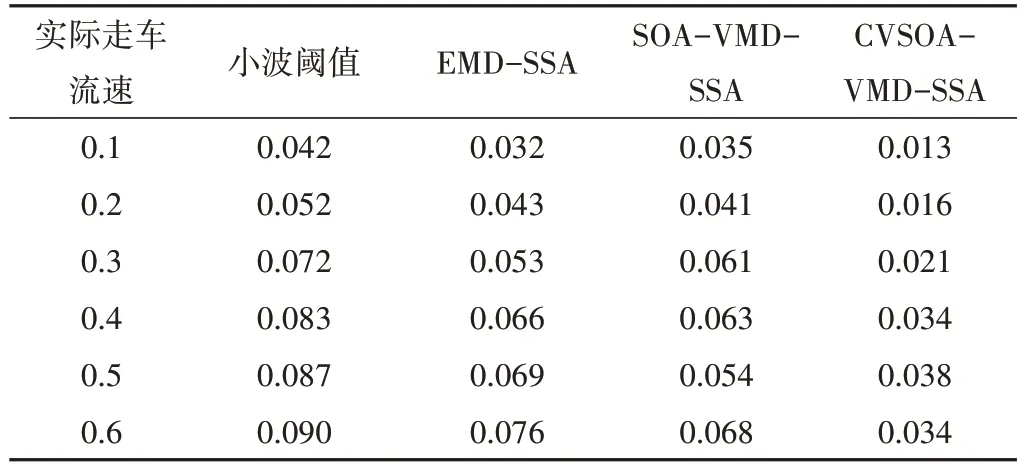
表4 不同走车流速探测精度对比 m/sTab.4 Comparison of the detection accuracy of different vehicle flow rate
由表4分析可知:CVSOA-VMD-SSA 相比于其他算法更利于随机噪声的抑制,随着流速的增加,几种算法误差也逐渐增大,但对比不同走车实测流速下的探测精度,CVSOAVMD-SSA 误差最小,范围在0.01~0.03m/s,为实际工程应用提供理论支撑。
4 结 语
本文利用CVSOA 对VMD 的参数进行优化,提出了将CVSOA-VMD 与SSA结合的方法,通过对模拟仿真信号和不同流速走车试验时间序列的降噪分析,验证了该方法的有效性和可靠性,并与WD、EMD-SSA、SOA-VMD 等方法对比分析,得出以下结论:
(1)模拟信号结果显示:CVSOA-VMD-SSA 能有效地去除噪声干扰,克服模态混叠及SOA 易陷入局部最优解问题,降噪信号的幅值及变化趋势得到完整地保留,与无噪原始信号存在差异最小,从评价指标看,CVSOA-VMD-SSA 明显优于其他几种算法。
(2)走车试验数据表明:采用多组信号统计分析可确定云相似度阈值为0.6,选用有效分量重构,并进行SSA 二次滤波降噪,CVSOA-VMD-SSA 能有效抑制噪声,对比不同走车流速探测精度,CVSOA-VMD-SSA 误差最小,范围在0.01~0.03 m/s,可为实际工程应用提供理论支撑。
