矩形渠道矩形侧堰水力特性试验研究
2023-09-16卢德友王莹莹张文正贾晓萌
卢德友,王莹莹,张文正,贾晓萌
(1.河南水利与环境职业学院,郑州 450011;2.中国农业科学院农田灌溉研究所,河南 新乡 453002;3.农业农村部节水灌溉工程重点实验室,河南 新乡 453002)
0 引 言
灌区用水的精准计量对执行最严格的水资源管理制度及农业以需定水、以水定地、以水定产至关重要。我国对于灌区量水技术的研究从20 世纪50 年代开始,经过70 a 以上的发展,量水技术和方法逐渐趋于成熟[1]。但是由于我国不同地区的灌区条件各异,存在不同的突出问题,如高含沙水的引黄灌区、坡降大的山区灌区和缓坡渠系的平原灌区,且各灌区工程类型和管理水平不一,因此,量水技术很难完全满足规范化、标准化现代灌区管理工作的需求,尤其是斗渠及以下的小型渠道量水设备的配套率还比较低。
薄壁堰流水位流量关系稳定,试验或野外测量时经常使用薄壁堰进行量水[2]。侧堰属于薄壁堰,其结构简单,量水精度较高,侧堰水力特性研究已经成为很多学者的课题。目前,国内学者对侧堰的研究主要集中在侧堰在水利工程中的应用[3,4],国外对于侧堰在灌溉工程中应用的研究较多。EMIROGLU 对矩形侧堰的水面线、流量系数等水力特性进行研究,并对基于流量系数推导出来的流量公式与其他学者进行对比[5]。ALIREZA 对不同侧壁坡度下的侧堰进行试验研究,并推导了含有佛汝德数、侧堰高度和侧壁坡度的流量公式[6]。前人对侧堰流量系数的研究较多,基于流量系数推导出的流量公式精度较高,但大多形式比较复杂,不便于推广应用。本文在王莹莹[7-9]、王佳伟[10,11]等人试验研究的基础上,补充分析了矩形渠道上的不同高度的矩形侧堰在不同流量工况下的水面线、壅水高度、水头损失等水力特性,推导了形式简单、精度较高、便于操作的流量公式,以期为侧堰优化选型和在小型渠道中的实践应用提供参考。
1 试验布置及方案
1.1 试验布置
试验渠道由2 条交角为90°的矩形渠道构成,分别为主渠道和侧渠道,主渠道长33.1 m、宽0.5 m、深0.6 m,为混凝土衬砌渠道,渠道综合糙率取为0.013,渠道底坡为1/2 000;侧渠道为PVC 材料制成的矩形槽,长2 m、宽0.5 m、深0.6 m。在渠道分水口处放置矩形侧堰。主渠道末端下游封闭,水流全部通过侧堰进入侧渠道。图1为试验系统平面图。试验系统流量大小通过阀门调节,测量校核使用直角三角形薄壁堰,即三角形薄壁堰堰顶夹角为90°,流量采用式(1)计算。渠道水深测量使用SCM60型水位测针,其测量精度为±0.1 mm。
式中:Q为过堰流量,m3/s;H为三角堰堰上水头,m。
1.2 试验方案
根据灌区小型渠道灌溉流量范围,本试验流量设置6个水平,分别为15.61、19.65、21.55、28.44、34.70、40.87 L/s;矩形侧堰堰宽均为50 cm,堰高设置6 个水平,分别为7.05、10.25、13.15、15.15、17.05、20.35 cm。为了获得主渠道侧堰附近水面变化情况,在侧堰上、下游端30 cm 范围内共设置9个测流断面。由于侧堰的泄流作用,主渠道垂直水流方向的水面会向侧堰倾斜,因此9个测量断面分别在靠近侧堰端(简称为①侧)、主渠道中心线(简称为②侧)和远离侧堰端(简称为③侧)3 处共计27 个测点进行水深的测量[8]。各测点具体位置如图2所示。

图2 试验测流断面位置及测点示意图(单位:cm)Fig.2 Schematic diagram of measuring sections and points
2 试验结果
2.1 水面线
渠道水深是量水的主要影响因素,水面线又是量水设施研究的主要影响因素,因此需要对主渠道侧堰段水面线进行研究[12]。水流从主渠道进入与其垂直的侧渠道时,水流流线发生急剧弯曲,水深也发生变化,由于侧堰的设置,各测流断面①、②、③侧的水深不相同。为了研究侧堰对主渠道水流的影响,绘制了各矩形侧堰在不同流量下的侧堰附近水面线。相似工况下规律相同,因此,本文仅对其中的一种工况进行分析。图3 给出了流量Q=15.61 L/s,侧堰高度h=7.05 cm 时不同堰高情况下主渠道侧堰附近水面线的变化情况,横坐标以主渠道水流流向为正方向,横坐标0点为断面V 所在位置,纵坐标表示渠道水深。由图3可知,随着水流的行进,主渠道侧堰上游段水面逐渐下降,在断面Ⅳ处下降到最低,这是因为在断面Ⅳ之后,水流流经侧堰上游开口处,高于堰顶的水流得以宣泄[7,10],水流流经侧堰时,因缓流条件下主渠道流量逐渐减少,侧堰段水面线逐渐上升[12],在侧堰下游段水面线逐渐趋于平稳。在同一堰高下,①侧水面线上下波动较大,②侧次之,③侧水面线较稳定,受侧堰的影响较小,这与前人研究的规律相同[7-11]。这说明侧堰的设置对主渠道水流的影响不大,影响范围仅限于主渠道中心线附近。
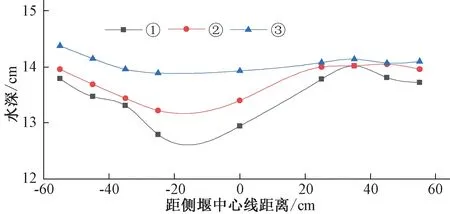
图3 Q=15.61 L/s,h=7.05 cm时主渠道侧堰附近水面线Fig.3 Flow profiles in main channel near side weirs when the discharge is 15.61 L/s and the side weir height is 7.05 cm
为了深入研究侧堰对主渠道水流的影响,绘制了同一堰高不同流量和同一流量不同堰高下①侧水面线,分别以堰高为7.05 cm 和流量为28.44 L/s 时为例(其他情况下规律亦同),如图4 和图5 所示,图4 和图5 的坐标设置与图3 相同。由图4可知,堰上水面线为壅水曲线,同一堰高下波动程度随着流量的增大而增大。由图5可知,同一流量下水深随着堰高的增加而增加,水面波动程度受堰高的影响较小。

图4 h=7.05 cm时不同流量下主渠道①侧水面线Fig.4 Flow profiles in main channel of side weir with height 7.05 cm under different discharges

图5 Q=28.44 L/s时不同堰高下主渠道①侧水面线Fig.5 Flow profiles in main channel of side weir with discharge 28.44 L/s under different side weir heights
2.2 壅水高度
在渠道上修建侧堰,会引起渠道上游水位壅高,造成一定范围内的淹没。设定渠道通过一定流量时,放置矩形侧堰前后渠道上游水深差为侧堰在该流量下的壅水高度[7]。为了使灌溉水流不因为侧堰的设置而溢出渠道,造成水源的浪费,需要对壅水高度进行分析。本试验对矩形侧堰在不同堰高、不同流量下的壅水高度进行计算,如图6 所示。由图6 可知,当流量一定时,壅水高度随着堰高的增大而增大。在同一堰高下,当堰高为7.05 cm 和10.25 cm 时,在流量小于28.44 L/s时,壅水高度随着流量的增加而减小,在流量大于28.44 L/s时,壅水高度随流量的增加而增加;当堰高在13.15~20.35 cm时,壅水高度整体上随流量的增大而减小,在流量大于28.44 L/s时,减小幅度较小,说明此时流量对壅水高度的影响较小。本试验条件下,不同堰高的矩形侧堰在不同流量下的壅水高度均在17 cm以内,最大壅水高度为16.14 cm。

图6 不同堰高下壅水高度随流量的变化Fig.6 Variation of percentage of backwater height with discharges under different side weir heights
2.3 水头损失
由于液体具有黏滞性,所以在流动过程中会为了克服各液层之间的摩擦阻力而做功,引起其机械能的损失,即水头损失[13]。量水设施在进行量水时都会产生一定的水头损失,进而导致灌溉效率降低,增加工程成本[14],因此研究量水设施时需对水头损失进行分析。水头损失根据液流边界的形状大小沿程变化与否和主流是否脱离边壁或形成旋涡分为沿程水头损失和局部水头损失[13]。对于本试验,水流顺主渠道流动,沿程形状大小不变,流经侧堰时产生分流,在主渠道侧堰下游产生漩涡,液层之间的摩擦和水质点间的碰撞加剧,进而产生水头损失。因此在侧堰流中的沿程水头损失与局部水头损失相比较小,可忽略不计[15,16]。在水头损失计算中,本试验选取的控制断面为主渠道中侧堰的上游端断面和侧渠道中的下游断面,基准面为渠道底部所在的水平面。
基于不同流量下各矩形侧堰试验数据计算水头损失,进而得到水头损失占上游总水头的百分比与流量之间的关系,如图7 所示。由图7 可知,相同流量下,水头损失百分比随堰高的增加而增加;同一堰高下,水头损失百分比随流量的增大而减小。当堰高为7.05、10.25、13.15、15.15、17.05 和20.35 cm 时,水头损失占上游总水头百分比的平均值分别为35.7%、43.7%、50.6%、55.3%、60.6%和65.5%,矩形侧堰的水头损失相比于大多槽类量水设施的水头损失较大[17,18]。

图7 不同堰高下水头损失百分比随流量的变化Fig.7 Variation of percentage of head loss with discharges under different side weir heights
2.4 矩形侧堰流量经验公式
通过对试验数据分析比较发现,流量Q与堰上水头h1有明显的函数关系,如图8所示。

图8 流量与堰上水头的关系Fig.8 Relationship between discharge and weir head
利用试验数据进行回归分析,获得各堰高下流量Q与堰上水头h1的关系式如表1所示。通过各关系式所得计算和实测流量的对比如图9 所示。由图9 可知,计算和实测流量的数据对比均在5%以内;由表1 可知,各公式最大相对误差绝对值为4.98%,最大平均相对误差绝对值为4.27%,满足GB/T 21303—2017GB《灌溉渠道系统量水规范》中对于量水精度不大于5%的要求[19]。

表1 各堰高下流量Q与堰上水头h1的关系式Tab.1 Relationship between discharge and weir head under different side weir heights
3 结 论
本文对矩形渠道中6 种不同高度的矩形侧堰在6 种不同流量下进行清水试验,并用三角堰进行流量校核,通过对试验所得数据进行分析,得到以下结论。
(1)获得了不同工况下主渠道侧堰附近水面线,因缓流条件下侧堰段主渠道流量逐渐减少,水面线均为壅水线,主渠道靠近侧堰一侧的水面受侧堰的影响波动较大。
(2)矩形侧堰的水头损失占上游总水头的35.7%~65.5%,水头损失较高,此性能指标劣于槽类量水设施。
(3)获得的流量公式最大相对误差为4.98%,满足GB/T 21303—2017GB《灌溉渠道系统量水规范》中对于量水精度不大于5%的要求。采用矩形侧堰量水时只需测得侧堰上游端水深即可获得过堰流量,具有简单、便捷、成本低廉且精准度较高的优点,便于在田间具有固定断面的硬化农渠(沟)、毛渠(沟)中应用和推广。
(4)影响矩形侧堰水力特性的因素还有渠道宽度、侧堰宽度、水流含沙量等,未来尚需要开展此3个因素与堰体结构的试验,以更好地提高侧堰量水精度。
