水面无人艇运动规划研究综述

高霄鹏，刘冬雨，霍 聪

(海军工程大学 舰船与海洋学院，湖北 武汉 430030)

0 引 言

随着计算机技术、通信技术和人工智能技术的发展与应用，越来越多的研究所、院校以及企业等机构开始研究并投入使用无人运载器[1]。无人运载器主要包括无人车、无人机、水面无人艇以及无人潜航器等[2]。由于能够高效率地完成危险艰巨的任务，无人运载器有着广泛的应用领域。例如，无人车（UGV）常被用于地震救援、考古研究、智能农业以及物流配送等领域[3]；无人机（UAV）则常被用于农业、航空拍摄、灾难救援、电力巡检以及军事打击等领域[4]。近年来，海洋资源的进一步开发和海上作战的需求促进了水面无人艇（USV）和无人潜航器（UUV）等海上无人装备的研发进度，同时也开拓了海上无人装备的应用领域，例如，海洋科考探测、海洋环境检测、海事搜救、水下地形勘测、海上牧场、海上运输补给、气象 探 测 以 及 军 事 作 战 等 领 域[5-8]。21 世 纪，我 国 提 倡共同建设“海上丝绸之路”，并多次强调海洋强国建设在经济发展和中国特色社会主义事业建设中的重要作用。因此，作为海上无人装备中的一种，USV 在未来海洋建设中必将发挥重要作用。

USV 作为一个复杂系统，其中包含众多子系统，如感知系统、载荷系统、控制系统、动力系统以及舾装系统等[9]，如图1 所示。各子系统相互配合，使USV 能够在复杂的海洋环境中实现自主航行。对于无人系统而言，自主航行能力是衡量无人艇智能化水平高低的一项重要指标。“自主”意味着USV 在不依靠任何人工控制手段的情况下，能够根据航行规则顺利完成任务。在整个过程中，根据航行环境与任务目标规划一条安全可靠的路径是USV 必须具备的一项功能模块，即路径规划模块。

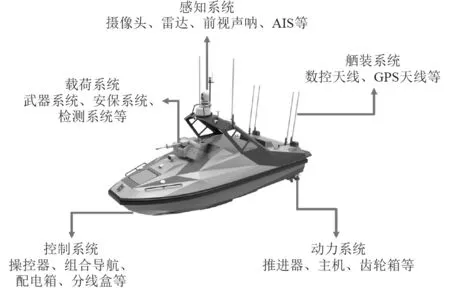
图1 无人艇系统构成Fig.1 The composition of USV

路径规划起源于早期的陆地机器人[10]，给路径规划模块输入起始位置、目标位置以及障碍物信息，为机器人输出一条可行路径。路径规划是一个优化问题，最明显的优化标准是距离[11]，即为机器人找到一条避开所有障碍物到达终点的最短路径。传统路径规划方法是将机器人视为一个质点，这对于UGV 和UAV 或许可行。对于UGV 而言，由于地理环境相对固定，且其具备紧急制动能力，所以其运动状态可控；UAV 在航行中会受到风等环境因素的干扰，但空中不存在复杂障碍物，在遇到紧急情况时，UAV 可悬停在空中。但对于USV 而言，传统路径规划方法存在一定不足。一方面，由于水域环境复杂，USV 会受到风、浪、流、水粘性力和惯性力等外界因素的干扰，即使USV 不做任何操作，也无法稳定维持在某一位置上。另一方面，大多数USV 是欠驱动的，无法在有限的空间范围内实现大角度转向操纵。因此，USV 的路径规划过程应考虑其实时的运动状态以及操纵能力边界。这便将路径规划问题由简单的路线规划上升为运动规划。运动规划过程考虑了USV 的所有动力学和运动学约束[12]，所以规划的路径符合USV 的航行特点，更有利于航行控制。随着无人技术的发展，无人艇路径规划研究逐渐朝向精细化的运动规划发展。

路径规划在某空间背景下，为USV 规划一条连续并符合规划要求的路径。根据发展阶段，文献将路径规划问题分为路线规划，轨迹规划和运动规划[13]3 类。路线规划是路径规划的初级阶段，该阶段将USV 视为一个质点，不考虑任何运动学和动力学特性，通常适用于大尺度区域的路径规划[14]，例如，USV 从大连港到上海港的路径规划，该路径无需考虑形状、速度等运动细节，如图2（a）所示。轨迹规划是路线规划的优化阶段，对路线规划的结果进行优化，主要优化指标包括航向角、曲率和速度等，通常适用于中等尺度区域的路径规划[15]，例如，USV到达港口附近时，需考虑如何进入内部端口，此时需考虑一些运动学约束，如USV 尺寸、航行速度以及回转半径等。运动规划是路径规划的高级阶段，除了考虑运动学特性外，还需考虑动力学特性，例如USV在六自由度上受到的力和力矩等，适用于小尺度区域内的精细路径规划[16]，例如，USV 在梳形路线巡航时，需知道如何完成直角转弯，如图2（b）所示。在此阶段，将USV 视为刚体，充分考虑运动过程中受到的所有约束以及实时运动状态变化，期望的规划结果是找到一条真实可控的路径。因此，以路径规划的3 个发展阶段为脉络，详细介绍了各阶段的规划方法以及研究与应用现状。

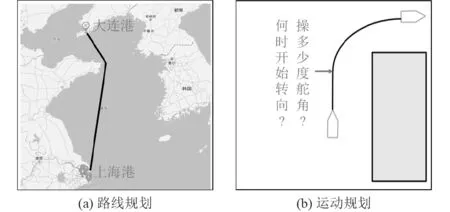
图2 路线规划与运动规划Fig.2 Route planning and motion planning

1 路线规划

在路线规划研究中，一般将规划对象视为一个质点，忽略运动学和动力学对规划效果的影响，例如百度地图为用户规划的行走路径、扫地机器人的路径规划以及游戏中角色的移动路线等。路线规划的相关研究相对较早，目前，已有许多经典搜索算法成熟应用于无人艇的路线规划中。根据算法特点分为传统路径规划算法、基于采样路径规划算法和智能仿生算法等。

1.1 传统路径规划算法

Dijkstra 算法、A*算法、人工势场法等都属于传统路径规划算法类型。其中最为经典的是Dijkstra 算法，该算法是Edsger Wybe Dijkstra 在1956 年提出的一种用来寻找最短路径的算法，主体思想是贪心思想[17]，即以起始点为中心向外层层扩展，每次扩展选择移动代价最小的节点作为下一节点，直到到达终点，搜索过程如图3（a）所示。Dijkstra 算法找到的路径一定是最优路径，但该方法扩展节点多，搜索效率低，导致在实际应用中存在诸多不足。1968 年，斯坦福研究院的Peter Hart 基于Dijkstra 算法提出了A*算法[18]，在路径代价函数中增加了启发项来使搜索方向逐步靠近目标点，A*算法的规划效果如图3（b）所示。A*算法不仅继承了Dijkstra 算法的优点，还减少了扩展节点的数量，节约了搜索空间，提高了搜索效率。

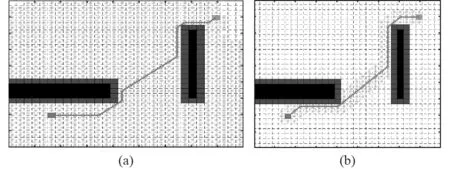
图3 Dijkstra 算法和A*算法Fig.3 Dijkstra algorithm and A* algorithm

人工势场法是由Khatib 于1985 年提出的一种基于虚拟力场的路径规划算法，该算法的基本思想是当机器人在环境中运动时，将环境设置为人造势场，目标点对机器人产生引力，障碍物对机器人产生斥力，引力和斥力的合力控制着机器人的运动方向[19]。该算法可以产生一条平滑安全的路径，但在距离目标点较远时，引力远大于斥力，可能导致机器人与障碍物发生碰撞。因此，人工势场法常被用于局部路径规划研究。

1.2 基于采样路径规划算法

基于采样路径规划算法更具灵活性，即使是同一规划任务，规划结果也可能不相同。基于采样路径规划算法的2 种典型算法是随机路线图算法（PRM）和快速搜索随机树算法（RRT）。PRM 算法的主要思想是基于图搜索的算法，通过在规划空间中生成随机的状态点来判断空间的可行区域位置，然后连接状态点找到可行路径[20]，过程如图4 所示。该算法适用于高维空间，常被用于无人机领域，这是因为无人机的路线规划是在三维空间进行的，PRM 算法不仅可以快速高效地搜索最优路径，还可以解决无人机多任务分配问题。RRT 算法通过对状态空间中的采样点进行碰撞检测，避免了对空间的建模，有效解决高维空间和复杂约束的路径规划问题[21]。该算法以初始点作为根节点，通过随机采样增加叶子节点的方式，生成一个随机扩展树，当目标点位于随机扩展树上时，停止增长，如图5（a）所示。但是，RRT 算法的规划结果往往不是最优的，针对这一问题，提出RRT*算法，缩短了路径长度。该算法的规划结果如图5（b）所示。

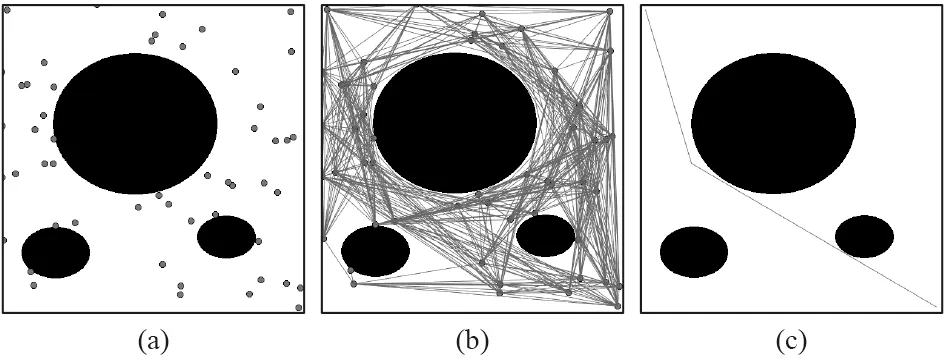
图4 PRM 算法Fig.4 PRM algorithm

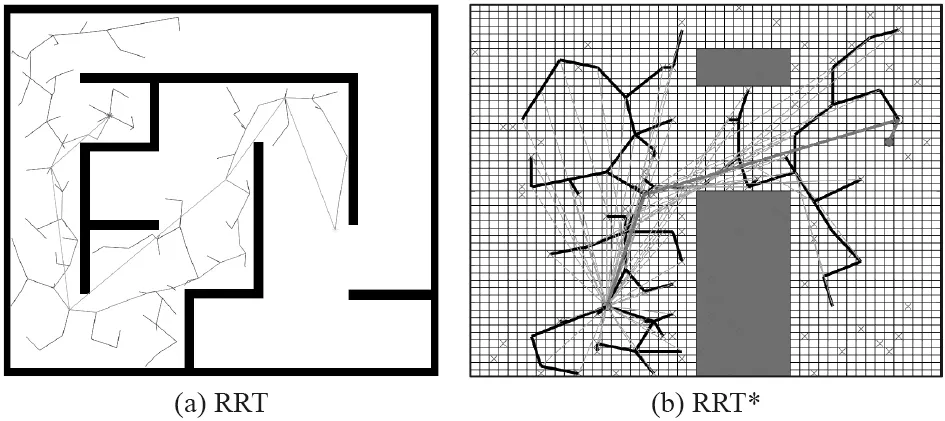
图5 RRT 算法和RRT*算法Fig.5 PRT algorithm and RRT* algorithm

Song 等[22]针对传统A*算法生成的路径折角多并存在多余节点的弊端，提出一种改进A*算法，其改进的核心思想是通过去除冗余节点使路径趋于平滑。Li 等[23]基于栅格法建立三维环境模型，使用D i j s t k t r a和A*算法实现三维路径搜索，该方法得到了较短的搜索路径，更具高效性和实时性，但是该方法搜索过程计算量大。为克服这个缺陷，又设计一种多方向A*算法，通过减少搜索点来获取更优路径[24]。张玉奎[25]使用遗传算法为USV 规划全局路径，进而使用人工势场法进行局部路径规划，2 种方法的结合缩短了规划时间，与单独使用某一种算法相比，得到的路径长度更短。

2 轨迹优化

轨迹规划是对路线规划结果的一种优化，规划目标是生成易于跟踪航行的路径。由于路线规划过程得到的路径是曲折的，对于USV 来说，其运动过程中具有惯性，无法突然转变航向。因此，路径曲率连续问题是轨迹规划过程中需要重点解决的一个方面。

2.1 曲线优化方法

常被采用的方法主要有Dubins 算法[26]、样条曲线法[27]、Clothoid 曲线[28]和费马螺线[29]等。Wang[30]在无人艇的路径规划中，使用二次B 样条曲线对路径点进行平滑处理，优化后的路径更适合USV 的实际航行。刘乐柱等[31]使用Dubins 算法为USV 规划一条曲率连续的路径，该方法首先根据USV 运动特性计算其转向能力，然后利用Dubins 曲线与回转圈的切线拼接得到平滑路径。

2.2 动力学约束方法

上述曲线拟合的方法需先获取路径点，再对点的连线进行优化。虽然满足了曲率的要求，但是对于USV 来说，还有一种效果更好的改进方法：即在路径规划算法中加入运动学的约束。Szczerba[32]等提出稀疏A*算法，使用最大转弯角度和最大路径长度作为约束条件，缩短了搜索时间，同时避免了路径中大转弯角度的出现。Kim[33]在二维路径规划算法的基础上引入曲率的约束，考虑动力学约束提出一个新的代价函数，虽然得到了更短的路径，但是改进之后还是包含较多的折线段，也未对路径进行平滑处理，所以得到的路径效果有待优化。Hanguen[34]基于传统A*算法，在搜索过程中考虑航向角和艏摇角速度的影响，实验表明，该算法在路径跟踪时间上优于三维A*算法。Lee[35]考虑了航向角的影响，根据欠驱动船舶的运动特性，将搜索子节点根据无人艇的实时航向信息变为3 个子节点，增加了搜索效率，同时删除了无人艇不能到达的节点。将船舶阻力和水深影响引入代价函数中，使无人艇航行过程的能耗降低。最后根据相邻路径点之间的可见性删除不必要路径点，同时考虑折线之间角度的大小，使算法效率提高。Wang[36]提出一种基于动态约束的全局-局部混合路径规划方案，通过全局路径规划算法生成相当稀疏的路径点，从而得到全局最优路径，通过控制纵向、横向速度和加速度，实现局部避碰。航行区域的水深影响着无人艇的水动力性能，水深不足将会引起搁浅等危险状况，Liu[37]通过分析无人艇的水动力模型，提出一种水深风险等级A*算法，在满足最短路径的同时考虑水深不足的危害，保证航行安全。传统A*算法在基于距离的代价函数作用下，导致生成的路径与障碍物距离较近，这不利于无人艇在具有复杂障碍物的水域上安全航行，Pc[38]综合考虑碰撞风险和路径与障碍物之间的距离，提出新的代价函数。根据船舶自身最大速度的约束计算障碍物碰撞风险，实验表明，相比于传统A*算法，该方法生成的路径安全性更高，更适合限制水域的路径规划。

3 运动规划

运动规划是路径规划的最终阶段，该过程求解的是无人艇具体要如何操作才能高效完成路径规划任务。因此，在运动规划阶段应综合考虑无人艇所有的运动学约束。这些约束可总结为轨迹约束、尺度约束、首向角约束。轨迹约束是指无人艇的操纵性能对运动规划过程产生的约束，即运动规划过程得到的轨迹必须满足曲率连续且符合无人艇最小回转半径的要求。根据无人艇的水动力性能可知，无人艇航行过程中的运动轨迹受到航速和舵角的影响：在一定航速下，转舵角度越大，回转圈越小；舵角不变时，航速越大，回转圈越小。如果想要无人艇始终稳定的按照规划的路径航行，就须考虑无人艇的实际操纵能力。

在运动规划研究中，要求无人艇能够精准识别自身运动状态，包括所处位置、速度以及首向角等。无人艇的首向角在一定程度上影响着其受到外界环境的干扰程度，同时也会影响跟踪期望路径的能力。由于大多数无人艇都是高度欠驱动型船舶，其运动轨迹受到自身操纵性能的约束，因此，无人艇几乎不可能在有限的空间内完成大角度转向。运动规划需全面考虑USV 的动力学和运动学约束，该方法可生成更加符合无人艇操纵性的全局路径。运动规划的研究是从无人车开始的，传统方法的一般步骤为：首先利用传统的路径规划方法，规划一条从起点到终点的无碰路径；然后，基于路径设计一个包含运动学和动力学约束的控制器，以驱动机器人安全快速地到达目标[39]。目前，流行方法是利用无人艇的操纵运动数学模型改善传统算法，Na[40]、Mingbo[41]、Jinze[42]等将无人艇的非完整约束与快速探索随机树(RRT)法相结合，RRT 算法的状态转换可通过运动学模型改进，新节点的生成可通过动力学方程施加约束。

Lu[43]采用概率地图法，并根据无人艇操纵性能约束进行改进，对操舵响应非线性模型进行线性化处理，考虑舵角饱和约束限制。Gu[44]根据水面无人艇的运动特性建立无人艇的运动单元库，解决了无人艇在限制水域中的运动规划问题。该方法同时满足无人艇的状态约束，机动特性约束和水深度约束。每个父节点拥有16 个子节点，搜索精度更高，但是，计算量庞大，无人艇的运动状态不连续。Han[45]提出一种预测轨迹的搜索算法，将由操纵模型生成的轨迹分解为栅格地图上的一系列的点，通过A*算法找到一条可行路径，在代价函数的启发项中引入了最大速度的影响，生成的轨迹可通过无人艇自身的操纵性能精准跟踪。但是，算法迭代次数多，更适用于短距离规划或离线规划。Du[46- 47]基于栅格地图，根据无人艇的运动数学模型来确定无人艇在不同舵角下的运动轨迹，建立轨迹单元；将由无人艇运动数学模型生成的轨迹作为路径规划的动态约束，在A*算法的代价函数中综合考虑了距离和转向的代价，可直接生成一条平滑的路径，但是该轨迹单元的栅格大小是固定的，限制了其应用情景。Willners[48]在水面无人艇追踪水下潜航器的应用背景下，根据无人艇的运动学模型，确定船舶的可行空间，可行空间有若干个分支组成，每个分支又离散成若干点作为分支的之间状态进行碰撞检测，这种搜索方式的状态连续，但是计算量庞大，实时路径规划时反应迟钝。

4 结 语

无人艇运动规划研究起步较晚，多数运动规划方法是基于传统路线规划算法，结合USV 的动力学模型或优化曲线到达最终规划目标。近几年国内外学者萌生了新的研究思路：将USV 的操纵性数学模型与栅格状态相结合，即将USV 的运动状态离散到栅格中，然后通过搜索算法选择并连接状态栅格，得到最终路径，这便演化为图搜索问题。A*算法是一种常用的图形遍历法，其较好的性能和准确度，对环境反映迅速，搜索效率高。在合适的代价函数的作用下，其找到的路径为最优路径，且A*算法与栅格模型结合的搜索效果较优，适合用于运动规划研究。

水面无人艇的运动过程复杂，路线规划和轨迹规划得到的路径并不利于航行控制模块对轨迹进行精准跟踪。针对这一突出问题，设计基于无人艇操纵性数学模型的运动规划方法是一种趋势：基于USV 操纵性数学模型，在搜索过程中考虑了USV 运动时产生的所有约束，改变搜索空间的构成；由于搜索空间的改变，导致A*算法中的避障方式无法适用于运动规划，因此，需要设定2 种避障规则：基础性避障和预测性避障；对代价函数进行改进，加入航向角改变代价，并将距离代价转换为相应的时间代价，更能反映实际航行代价。为了使规划的路径更加符合无人艇的操纵运动特性，使用无人艇的操纵运动模型进行轨迹预测，实现对路径点进行平滑处理，使平滑路径的运动状态连续，更利于无人艇控制系统的跟踪。 另外，针对不同尺度的地图模型和不同的任务背景，应分析栅格尺度对运动规划效果的影响。