混凝土重力坝水力劈裂分析及渗流-应力耦合模型构建

赵文赞,林 毅

(雅砻江流域水电开发有限公司,成都 610051)

0 引 言

混凝土重力坝是一种大型水工结构,被广泛应用于各种水利工程中[1]。由于其体量庞大、承受的载荷巨大,混凝土重力坝往往会在动静载荷作用下产生各种问题,其中最为普遍和严重的问题是水力劈裂与渗流[2]。水力劈裂是指水力作用下坝体内应力产生断裂,导致液体在混凝土坝体内穿过的现象,严重时会危及重力坝的安全稳定。渗流是指水流在坝体内部发生渗透现象,从而影响坝体稳定性[3-4]。这两种问题都会导致混凝土重力坝的破坏,甚至造成严重的后果。

拓展有限元法是将富集函数引入到有限元近似中,可以通过和附加自由度相关联的函数确定裂缝的不连续性,进而对裂缝的几何不连续进行模拟[5]。扩展有限元法是对传统有限元方法的补充,能够考虑到非连续介质的影响,可以更加真实地反映材料的非连续性和各向异性。同时,考虑了材料内部的裂纹,可以更准确地计算材料内部裂纹的扩展行为,扩展有限元法在建筑结构裂缝分析得到了广泛应用[6-7]。

为了解决因水力劈裂与渗流问题而导致的混凝土重力坝破坏与安全隐患,本文利用有限元分析等方法,构建应力耦合模型,研究成果可为混凝土重力坝裂缝分析等提供理论依据。

1 基于渗流-应力耦合效应的混凝土重力坝水力劈裂分析

1.1 水力劈裂的渗流-应力耦合模型

在水工建筑物中,混凝土重力坝是其中较为重要的建筑之一。在混凝土坝中,当坝体出现裂缝并产生扩展时,会导致混凝土坝失效,坝体遭到破坏[8-10]。严重时,甚至会使混凝土重力坝的运行出现异常,严重威胁周边人员的生命财产安全。因此,对混凝土重力坝裂缝产生和扩展的原因进行分析,是保护混凝土重力坝安全的重要环节之一。

在水力劈裂中,存在相互作用的两相介质,即库水和混凝土,这两者之间存在渗流-应力耦合效应。在渗流-应力耦合方程中,存在两种耦合方式,即强耦合方式和弱耦合方式[11-13]。耦合方程由两部分组成,分别为应力平衡方程和连续性方程。对于强形式的控制方程而言,当同向性多孔材料处于准静态状态下,其应力平衡方程数学表达式如下:

∇*σ+ρb=0

(1)

式中:∇为梯度算法;σ为总应力;b为体力矢量;ρ为饱和多孔介质的平均密度,ρ=(1-φ)ρs+φρW;ρs为固相的密度;ρW为液相的密度。

对于多孔介质渗流而言,其连续性方程的数学表达式如下:

(2)

当忽略加速度的影响后,流体在孔隙内流动的过程中会遵循相关定律,该定律为达西定律。此外,对于多孔介质的本构方程而言,当其通过有效应力的形式进行输出时,可以得到有效应力的相关数学表达式,具体公式如下:

σ′=σ+φmp=Dε

(3)

式中:σ′为有效应力;ε为孔隙介质的应变张量;u为孔隙介质的张量位移;φ为多孔介质中的孔隙度;p为多孔介质中的孔隙水压力;D为平面应变刚度矩阵;m为常向量。

对渗流-应力耦合方程中的弱形式控制方程进行研究。在相关研究过程中,对于在水力劈裂有限元模型而言,其涉及的相关裂缝存在几何不连续性[14-15]。将位移函数设置为δu,将孔隙水压力试函数设置为δp,将式(1)、式(2)的两端各自乘以δu和δp,并分别进行积分运算,运算所在的区域为区域Ω。然后对散度定理进行应用,并施加裂缝处的边界条件,从而得到渗流-应力耦合方程中的弱形式控制方程,即弱形式下平衡方程和连续性方程。从弱形式的控制方程中可以看出,裂缝与渗流场和应力场之间的影响情况。

在裂缝的损伤演化模型中,主要采用内聚力模型。内聚力模型属于一种唯象模型,归属于弹塑性断裂力学领域,应用较为广泛。学者们根据不同材料所具有的损伤破坏特征,提出了众多内聚力模型的张力位移关系,主要包括双线性、梯形、指数型以及多项式等形式。具体采用的弹性模型见图1。

图1 相关弹性模型

图1中,δmax为函数最大值;tp为边界Γt的面力。

1.2 基于XFEM的混凝土重力坝中水力劈裂分析及验证设计

完成对渗流-应力耦合方程的两种情况分析后,在进行水力劈裂数值计算时,选择扩展有限元法(Extended finite element method,XFEM),并得到基于XFEM的“虚拟节点”法形式,进行虚拟节点的应用。该类节点叠加在原始真实节点之上,通过该虚拟阶段,对结构裂缝的不连续性进行表示。在单元处于完整状态时,真实节点会完全对其对应的虚拟节点进行约束;在单元处于被裂缝穿过的状态时,裂缝所在的路径会将单元切割成两部分。经过裂缝扩张后,真实节点和其对应的虚拟节点呈现出分离状态,这两种类型的节点不再处于捆绑状态。其中,可将虚拟节点表示为三角形点,见图2。

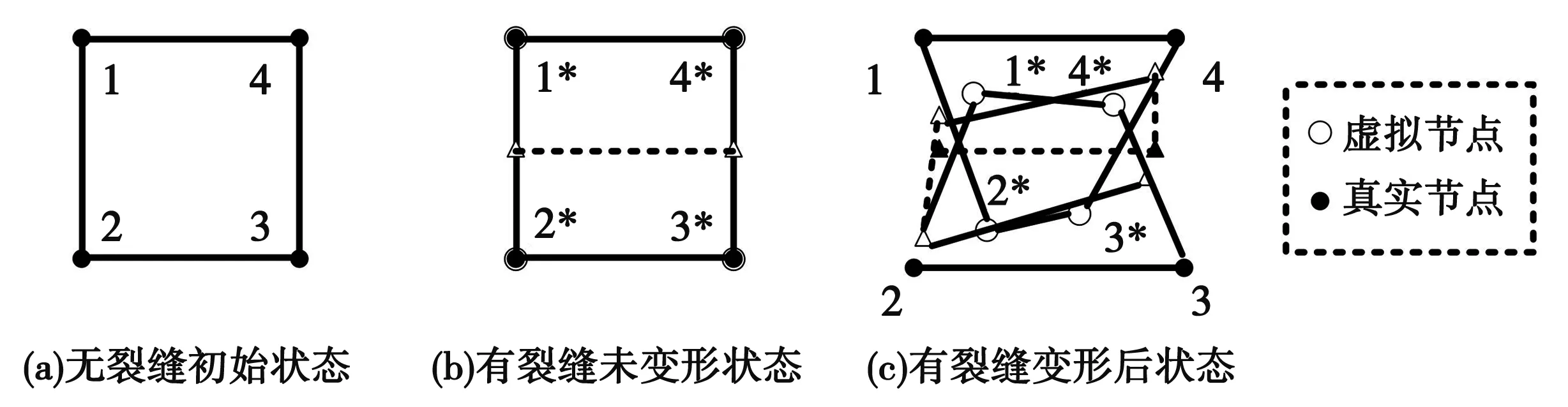
图2 XFEM虚拟节点

由图2可知,不同裂缝状态下,真实节点和虚拟节点之间的位置关系存在差异。相对于图2(a),图2(c)中真实节点和虚拟节点之间的位置发生了较大的变化,虚拟节点分布在真实节点周围,将真实节点包围起来。

在对裂缝顶部和底部的空隙水压力进行求解时,首先获得角点处虚拟和真实两种节点的孔压插值,通过该插值可以得到所求的空隙水压力。通过对裂隙边缘的虚拟节点进行插值,得出的裂隙水压强是裂隙水压强变化的驱动力。对于每个XFEM加强单元而言,在其边缘上进行附加虚拟节点的引入,该节点具有空隙自由度,将该节点与图2中的节点组合起来,对断裂单元表面的流体流动进行模拟。通过这种形式,对不连续性断裂单元中的相关情况进行表示,可以从中看出其位移和流体压力的情况。对于裂缝单元而言,在其水压力的作用下,加强单元会出现力分离行为。在此基础上,可对水力劈裂的裂缝模型进行建模。

针对研究的方法进行数值验证,选择某高混凝土重力坝,该重力坝高100m。在研究中,将其挡水坝段作为研究对象,该重力坝的初始裂缝在坝踵处,裂缝长0.5m,所在位置与建基面处于一个水平面。在挡水坝段的模型中,其材料有3种,即坝体采用的材料为混凝土;坝基采用的材料为岩石;建基面采用坝体和坝基所采用的材料,建基面厚1m。此外,挡水坝段模型的相关材料部分参数见表1。

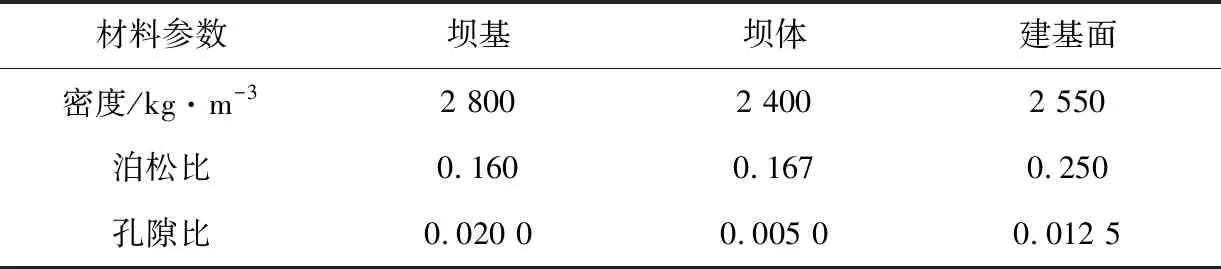
表1 部分材料参数

从表1可以看出,挡水坝段模型3个组成部分的部分材料参数存在差异。重力坝部位不同,同一参数下对应的值不同。

2 水力劈裂问题的结果分析

为验证所给出方法的有效性,本研究进行以下一系列实验,并设置对比方法[16]。鉴于裂缝口的水压力将会受到裂缝口流量的影响,试验首先分析注水率不同情况下裂缝口水压力的变化趋势。见图3。由图3(a)可知, 参考文献的解与研究所求得的数值解在时间变化序列中表现出相似的变化规律。整体表现为裂缝口水压力快速增加至峰值1.78MPa,此时相应的时间为0.45×10-3s。随后裂缝口水压力随着时间的增加而缓慢降低,并逐渐趋于平稳值,约为0.48MPa。由图3(b)可知,裂缝口水压力和注水率表现出较强的关系。整体而言,裂缝口水压力在时间序列中表现出急速增加随后逐渐下降的变化趋势。以时间点0.16×10-3s两端为例,在相同的时间点,裂缝口水压力和注水率表现出正向变化规律,即随着注水率的增加,裂缝口水压力也呈现逐渐增加的变化规律。注水率越大,则裂缝口水压力下降的幅度越大,同时达到收敛值的时间越短。当注水率为1×E-5m2/s时,裂缝口水压力的稳定收敛值为1.12MPa;当注水率为20×E-5m2/s时,裂缝口水压力的稳定收敛值为0.01MPa。

图3 数值解的对比和不同注水率下裂缝口水压力的变化规律

结构安全性的重要评价指标为裂缝张开位移,试验分析数值解的对比和不同注水率下裂缝张开位移的变化规律,结果见图4。由图4(a)可知,参考文献的解与研究所求得的数值解在时间变化序列中表现出相似的变化规律。裂缝张开位移在时间序列中表现出逐渐增加的变化规律。当时间为8.0×10-3s时,裂缝张开位移文献解和本文解分别为6.12×10-3m和6.11×10-3m。从图4(b)可知,裂缝张开位移和注水率表现出较强的关系。整体而言,裂缝口水压力在时间序列中也表现出近似正向的变化趋势。注水率的数值越高,则裂缝张开位移越长。以时间点8.0×10-3s为例,当注水率为1×E-5m2/s时,裂缝张开位移为0.46×10-2MPa;当注水率为20×E-5m2/s时,裂缝张开位移为5.42×10-2MPa。因此,不同的注水率对裂缝张开位移有着较为明显的影响。

图4 数值解的对比和不同注水率下裂缝张开位移的变化规律

注水率对建基面的降水压力和竖向位移均有不同程度的影响,试验分析结果见图5。由图5(a)可知,当注水率为1×E-5m2/s时,孔隙降水压力的最低值为-0.42MPa;当注水率为20×E-5m2/s时,孔隙降水压力的最低值为-0.38MPa。由图5(b)可知,当注水率为1×E-5m2/s时,竖向位移的最大值为3.85×10-4m;当注水率为20×E-5m2/s时,孔隙降水压力的最低值为0.01×10-4m。整体而言,在不同注水率下,降水压力和竖向位移均与注水率表现出较强的关联性。孔隙降水压力和竖向位移在不同注水率下达到最低值和最高值的时间呈现前后差异,其中注水率越小,达到峰值的时间越短。同时,注水率越小,峰值的最大值越小。这可能是由于随着注水率的不同,水压导致裂缝扩展的长度呈现不同的情况分析不同沿建基面距离下不同渗透系数对应的竖向位移和孔隙压力情况,结果见图6。由图6(a)可知,渗透系数和建基面距离不同,对应的孔隙压力存在差异。总体上,在相同渗透参数下,随着建基面距离的增大,孔隙压力呈现出先减小后增大的趋势。在渗透系数k为5e-9m2/(Pa·s)中,当沿建基面距离为10m时,对应的孔隙压力为0.36MPa,比沿建基面距离为20m时大0.24 MPa;当沿建基面距离为70m时,对应的孔隙压力为0.33MPa,比沿建基面距离为60m时大0.15MPa。在沿建基面距离为60m中,当渗透系数为1e-9m2/(Pa·s)时,对应的孔隙压力为0.46MPa,比其他渗透系数下的孔隙压力均大;当渗透系数为25e-9m2/(Pa·s)时,对应的孔隙压力为-0.31MPa。由图6(b)可知,渗透系数、建基面距离对竖向位移的影响不大,特别是当处于下游面附加处时,不同渗透系数下的竖向位移相差很小。

图5 注水率对建基面的降水压力和竖向位移的影响

图6 相关竖向位移和孔隙压力

3 结 论

为了分析混凝土重力坝水力劈裂形成机制,以混凝土重力坝为研究对象,对其渗流-应力耦合方程的两种形式进行分析,通过XFEM算法计算相关数值。结果显示,裂缝口水压力在时间序列中表现出急速增加随后逐渐下降的变化趋势,注水率分别为1×E-5和20×E-5m2/s时,裂缝口水压力的稳定收敛值为1.12和0.01MPa;裂缝张开位移在时间序列中表现出逐渐增加的变化规律,当时间为8.0×10-3s时,裂缝张开位移文献解和本文解分别为6.12×10-3和6.11×10-3m。孔隙降水压力和竖向位移在不同注水率下达到最低值和最高值的时间呈现前后差异,注水率越小,达到峰值的时间越短,且峰值的最大值越小。