1992-2020年齐齐哈尔市降水量变化特征分析

王千凤,陈 末,齐新虎,袁晓阳,刘袁媛

(黑龙江大学a.水利电力学院;b.寒区地下水研究所,哈尔滨 150080)

0 引 言

在整个水资源体系中,降水量指标尤为重要。降水量的变化程度以及覆盖范围对旱涝灾害产生相当部分的影响,进而影响农业生产等活动[1]。无论是从预测灾害的角度,还是从农业管理的角度上来考虑,针对降水预报的研究都是十分有益的[2],因为降水导致的不同程度的气象灾害也是全球共同关注的。

近年来,许多学者对齐齐哈尔市的降水情况进行了多方面的相关研究。许亚杰[3]以地理加权回归模型,对齐齐哈尔市各个季节的降水分布进行了研究。娄德君等[4]分析了当地2001年以前近40年的降水时空变化特征。王洪宝[5]利用BP神经网络模型,对齐齐哈尔市的降水预测进行了研究。田媛[6]利用1961-2013年齐齐哈尔市的降水数据,采用五点滑动平均法、线性趋势法、M-K突变检验法等,分析了当地的年降水量、各季节降水量的变化趋势及突变位置。

本文选取五点滑动平均法[7]、线性趋势法[8],分析齐齐哈尔市近29年的年降水量及各季节降水的变化趋势,并采用M-K突变检验法[9],确定变化的突变年份。

1 数据来源与方法

1.1 研究区概况

齐齐哈尔市以鹤城著称,属于黑龙江省辖地级市,齐齐哈尔市内共有7区8县。齐齐哈尔市地处东北地区的松嫩平原,土地资源丰富,水资源充足,市内主要河流170多条,水质天然良好;属于温带大陆性季风气候,四季鲜明,夏季降雨较为充沛,同时也具有东北地区普遍旱涝、低温、大风的气候条件。受气候条件影响以及地理位置因素,对农作物的生产有程度不同的显著差异。

1.2 数据来源

本研究内容中的齐齐哈尔市水文降水数据来源于中国气象数据共享网。选取齐齐哈尔市1992-2020年近29年的逐日实测降水数据,逐日降水数据经过累加处理,得到近29年的月降水量数据以及年降水量数据。

1.3 研究方法

本文针对齐齐哈尔市的降水量进行趋势性分析以及突变性分析。其中,趋势性分析采取距平百分率法、线性回归法、滑动平均法;突变性分析采取Mann-Kendall突变分析法。

1.3.1 距平百分率法

距平百分率法是一组数据同期的实测值距离该组数据平均值的大小与该组数据平均值的比值,运用距平百分率法的好处是可以体现一组序列的变化程度,所以距平百分率就是对距平进行了标准化处理,可以直观体现降水量的变化程度。

1.3.2 线性回归分析法

线性回归分析法是典型的数理统计方法,是定量处理两组或多组变量之间相互依存关系的一种分析数据方法,在处理一组数据随着一种因素的变化而变化时被广泛使用。本研究采取一元线性回归分析,自变量为降水年份x,因变量为年降水量y,建立最小二乘法的一元线性回归方程为:

(1)

1.3.3 滑动平均法

滑动平均法常用于水文序列的趋势成分识别,可使原序列光滑化,便于判断原序列的趋势。假设原序列为x1、x2、x3、…、xn,则新序列计算公式如下:

(2)

式中:yt为新序列:当k=2时为5点滑动平均。

1.3.4 曼-肯德尔法

又称Mann-Kendall检验法,简称M-K检验法。M-K检验法通常适用于针对在气候变化条件下影响的降水等趋势检测,是一种非参数检验法,也叫无分布检验。这种检验方法的好处是选取的样本不需要遵守固定的分布,少部分数值异常的点不会对其产生干扰。假定时间序列为x1、x2、x3、…、xn,M-K趋势检验的统计量如下:

(3)

式中:xj为时间序列的第j个数据值;n为样本长度。

(4)

假定时间序列为随机的条件下,定义统计量为:

(5)

(6)

(7)

将时间序列逆序排列,按式(3)-式(7)计算UBk,并且满足UBk=-UFk,若取显著性水平α为0.05时,临界值U0.05=±1.96。当UFk>0,表示序列有上涨的趋势;UFk<0时,表示序列有下降趋势;若|UFk|>1.96,则表示序列显著上涨或下降。当在临界区域内,UBk与UFk的交点即为突变发生的时间。

2 结果与分析

2.1 齐齐哈尔市多年降水量变化

2.1.1 齐齐哈尔市降雨量年代际变化

从表1中可以看出,齐齐哈尔市近29年的年代际降雨量总体上呈增长状态,年代际降雨量最高的年区间为2013-2019年,为475.41mm;1999-2005年的平均降雨量最少,为395.57mm,这6年处于少雨阶段。最高年区间与最低年区间的平均降雨量相差79.84mm。

表1 1992-2019年齐齐哈尔市年代际降雨量变化

2.1.2 齐齐哈尔市降雨量年际变化

由图1可以看出,齐齐哈尔市近29年的最高年降水量为2013年,高达626.3mm;其次是2020年的年降水量,为625.4mm;年降雨量最小的年份是2001年,为250.3mm。齐齐哈尔市年降水量的总体趋势呈逐年递增状态,每年约递增5mm。根据滑动平均的计算结果来看,1992-2020的年降水量呈先下降后上升再下降的总体趋势。

图1 年降水量线性趋势法及滑动平均法处理结果

由图2中的UFk曲线变化可以看出,2006年以前降水量总体呈现下降趋势,从2006年后年降水量具有上升趋势。根据UFk和UBk两条曲线相交情况可知,年降水量突变年份为2009及2016年。

图2 M-K年降水量突变检验结果

由图3齐齐哈尔市年降水量的距平百分比可以看出,齐齐哈尔市近29年的年降雨量距平基本呈现正负交替状况,距平百分率呈先减少后增加再减少再增加的趋势,表明降雨量也呈先减少后增加再减少再增加的趋势。

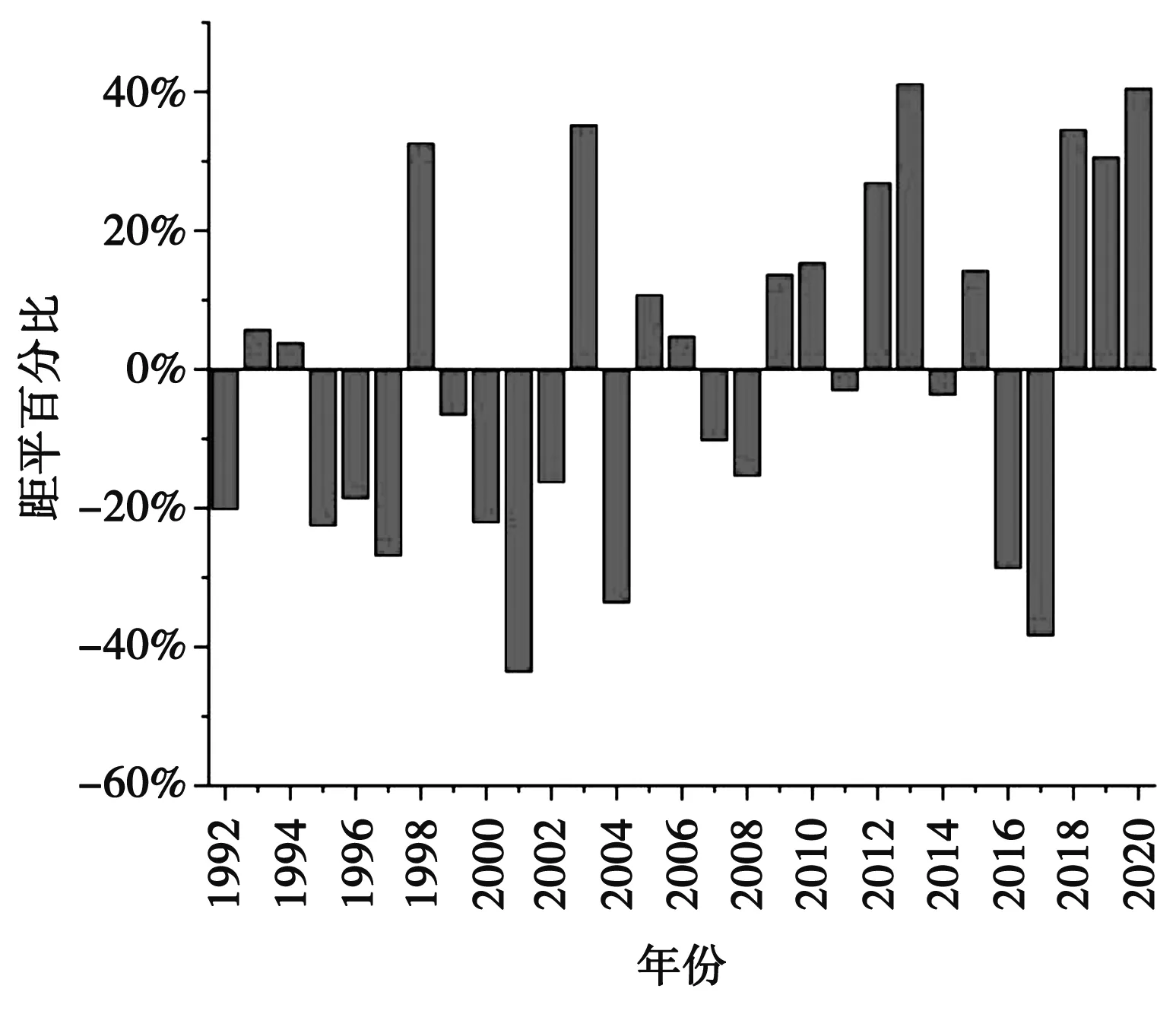
图3 1992-2020年年降水量距平百分比

2.2 各季节降水量变化趋势分析

按照四季时间,通常划分春季为3-5月份,夏季为6-8月份,秋季为9-11月份,冬季为12月份至次年2月份。通过逐日累加齐齐哈尔市近29年的日降水量,得到近29年的四季降水量。对四季降水量进行趋势分析,通过图4-图7观察发现,1992-2020年齐齐哈尔市的各季节降水量总体都呈现上升趋势;夏季的降水量增长率最大约为2.6mm每年;冬季降水增长率最小,仅为0.2mm每年。根据滑动平均法的分析结果可以看出,春冬两季的降水量呈先上升后下降的趋势;夏季呈不太明显的先上升又下降的趋势;秋季则呈明显的先下降后上升的趋势。

图4 春季趋势分析结果

图5 夏季趋势分析结果

图6 秋季变化趋势分析结果

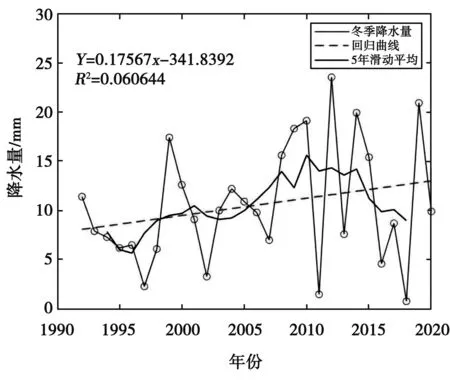
图7 冬季变化趋势分析结果

2.3 各季节降水量变化突变分析

根据M-K突变检验分析可得到结果,见图8-图11。春季降水的突变年份大致为2003及2016年;齐齐哈尔市夏季的降水相对情况较为复杂,对于突变点的检验较为困难;秋季降水的突变发生在2015年;冬季降水的突变年份发生在2003年。

图8 春季突变分析结果

图9 夏季突变分析结果

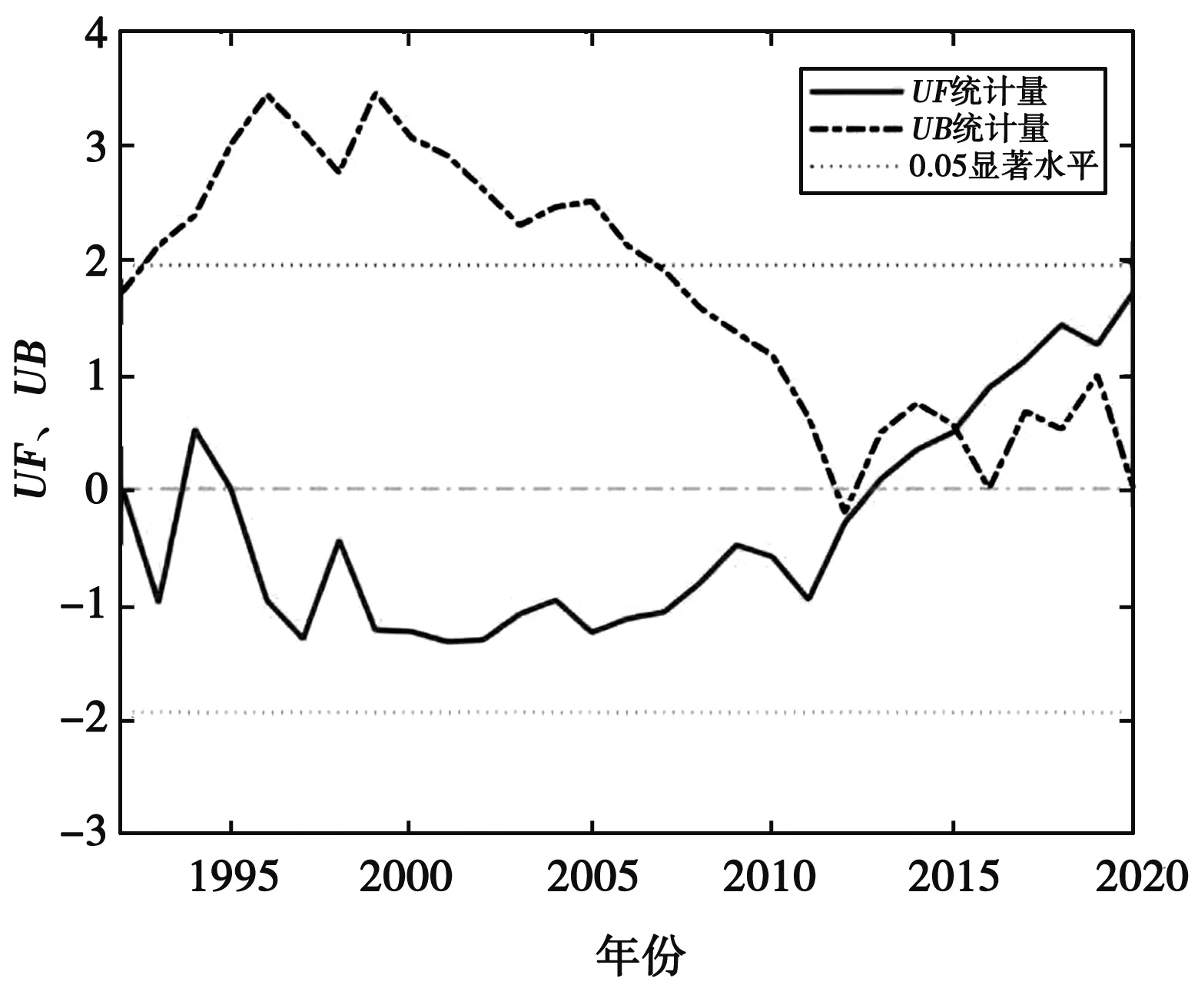
图10 秋季突变分析结果

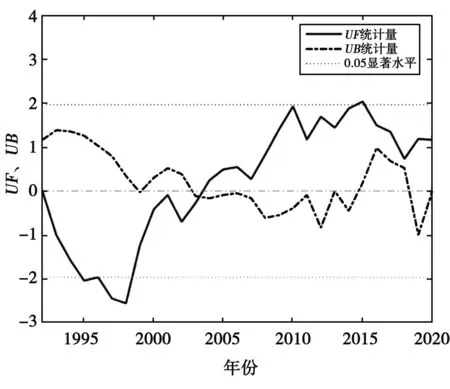
图11 冬季突变分析结果

3 结 论

通过距平百分率法、线性回归分析法、滑动平均法、曼-肯德尔法,对齐齐哈尔市1992-2020年的年降水量、四季降水量分别进行趋势分析以及突变检验。结论如下:

1)通过分析齐齐哈尔市年降水量变化,结果表明,齐齐哈尔市年降水量总体呈上涨趋势,每年上升约5mm。通过突变分析,确定突变年份为2009及2016年。年降水量最高年份与年降水量最低年份的降水量相差373mm,降水量的波动幅度较大。

2)通过分析齐齐哈尔市四季降水变化可知,春季、夏季、冬季均呈现先上升后下降的趋势;秋季降水则是先下降后上升。通过突变分析,确定了春季降水发生突变的年份为2003、2016年;秋季降水发生突变的年份为2015年;冬季降水发生突变的年份为2003年。由于齐齐哈尔市的地理位置以及气候条件,其降水多集中在夏季,因而夏季的降雨较为密集,分析起来相对困难。