基于改进MOMEDA的变转速滚动轴承故障诊断
2023-09-15许伟
许伟
(上海电气集团股份有限公司 中央研究院,上海 200070)
1 概述
滚动轴承是旋转机械中极为关键的承载部件,广泛应用于航天、冶金、交通、新能源等领域。如果不能及时发现并消除意外故障,可能会导致机械设备进一步劣化,造成异常停机等严重后果,因此滚动轴承早期故障诊断具有重要研究意义。在滚动轴承失效进程的早期,故障冲击振动信号往往十分微弱,容易被背景噪声和其他干扰所淹没,失效特征难以准确提取,需进行早期故障特征增强方法的研究。
基于滤波的方法可有效提高故障特征的提取效果,其关键在于设计滤波器或通过解卷积优化滤波器。解卷积方法具有灵活性和自适应性,最小熵解卷积(Minimum Entropy Deconvolution,MED)是一种经典的解卷积方法[1],其将峭度作为信号冲击性的度量,构建逆滤波器并提取故障脉冲。尽管MED在多种应用中都有不错的效果,但易受到背景噪声和冲击干扰的影响[2-7]。为进一步改善MED的应用效果并增强周期性故障特征提取能力,文献[8]提出了一种基于最大相关峭度解卷积(Maximum Correlated Kurtosis Deconvolution,MCKD)方法,其引入了相关峭度(CK)作为判据,通过考虑故障脉冲的周期性有效抑制了不同故障脉冲之间的相关性:文献[9]在MCKD中加入故障特征周期的自适应估计,提高了该算法的效率和鲁棒性;文献[10]将MCKD作为后处理方法,结合自适应局部迭代滤波提取故障脉冲特征,并用粒子群算法对解卷积参数进行优化。尽管MED和MCKD有多种改进方法,但本质上都基于峭度最大化。由于峭度是高阶统计量指标,利用目标函数法只能通过迭代进行求解,上述方法效率有限且求解结果可能仅是局部最优解。
在实际应用中,解卷积方法的性能主要取决于判据的选择。文献[11]将最小广义Lp/Lq解卷积与谱峭度结合用于滚动轴承故障特征提取,文献[12]提出了基于基尼指数的盲解卷积方法框架,但上述方法仍然被迭代问题所困扰。文献[13]提出了一种称为D范数的解卷积判据,并提出了最优最小熵解卷积(Optimal MED,OMED)方法,其与MED在几何上等价,但却无需迭代过程。文献[14]对OMED方法进行了改进,通过调整Toeplitz矩阵消除了由数据不连续带来的虚假脉冲并将其命名为最优最小熵反褶积调整(OMED Adjusted,OMEDA)。与MCKD类似,OMEDA中进一步针对故障特征的周期性提出了多点最优最小熵解卷积调整(Multipoint OMEDA,MOMEDA)方法,虽然相对于MCKD并不能有效增强提取效果,但效率有明显提高。在实际应用中可通过优化滤波器长度、实际故障周期等参数以获得更好的提取效果。
上述方法多应用于工况稳定的情况,而大多数机械装备都很难保证平稳的服役工况,也导致基于周期性的解卷积方法在很多情况下特征提取能力有限。为解决这个问题,文献[15]基于故障特征的二阶循环平稳性最大化准则开发了最大二阶循环平稳盲解卷积(Maximum Second-order Cyclostationarity Blind Deconvolution,CYCBD)及其改进方法CYCBDang,此类方法可以使用测得的瞬时转速在转速非恒定时精确提取故障脉冲,与其他解卷积方法相比有很大的优势。文献[16]提出了最大平均峭度解卷积(Maximum Average Kurtosis Deconvolution,MAKD),其根据循环频率对滤波后的信号进行分割并将信号片段的平均峭度作为判据,不仅适用于变转速工况,而且能很好地抑制随机干扰的影响。与经验模态分解、阶次跟踪等[17-18]经典变转速故障诊断方法相比,上述解卷积方法可以在不进行重采样或不受模态耦合影响的情况下突出故障分量,但仍需通过迭代求解。此外,阶次跟踪、广义解调等非平稳信号处理方法在恢复信号平稳性的同时会导致信号中时不变共振特征的缺失或损坏,给后续的特征提取带来很大困扰。因此,如何在变转速工况下快速有效地识别滚动轴承早期故障仍然是一项具有挑战性的任务。
为满足上述要求,本文提出了一种改进多点最优最小熵解卷积调整(Improved Multipoint Optimal Minimum Entropy Deconvolution Adjusted,IMOMEDA)方法,在不进行重采样,不破坏时不变共振特征的前提下,首先,根据脉冲在角度域的等角度分布特性计算故障脉冲的时域间隔并构成目标向量,使循环频率随转速动态变化,实现故障特征的表征;然后,在将其扩展到变转速工况的同时,通过分段计算多D范数保证原有的高计算效率;最后,引入包络谐波强度进一步自动定位滤波信号的循环调制阶次,为故障诊断提供依据,以实现滚动轴承早期故障特征提取。
2 MOMEDA解卷积方法原理
在恒定转速条件下,局部故障引起的脉冲力周期性地激励在旋转部件上使机器产生共振,这种共振可以被振动传感器获取,但易被各种干扰所埋没。为增强故障信息,MOMEDA采用新的解卷积方式设计滤波器,使滤波信号中的脉冲分量最大化。
假设给定的振动信号为x=[x1,x2,…,xN]T,MOMEDA的目标在于找到最优逆滤波器,使滤波信号y的多D范数最大化。多D范数的表达式为
(1)
基于最大化目标函数,假定逆滤波器f可表示为长度L的FIR滤波器,则MOMEDA可变为以下优化问题,即
(2)
式中:t为确定脉冲位置和权重的目标向量。通过设计合适的目标向量t,可以对任意位置和任意权重的目标脉冲进行解卷积。通过求解多D范数的最大值获得最优逆滤波器系数,进而获得最终的滤波信号。
对逆滤波器系数求导可得
(3)
其中
(4)
Mk=[xk+L-1,xk+L-2,…,xk],
(5)
(6)
则(3)式可写为
(7)
t1M1+t2M2+…+tN-LMN-L=X0t。
(8)
通过导数等于0求解极值可得
(9)
即
(10)

(11)
由于任意倍数均为(11)式的解,所以MOMEDA的逆滤波器和输出解可表示为
(12)
(13)
3 IMOMEDA方法
使用MOMEDA提取周期性脉冲时,目标向量t中的非零元素是周期性的,从而可以捕获故障脉冲的位置;但当机械设备转速具有明显时变时,故障部件的时域周期性就不再成立,MOMEDA的提取效果不佳。尽管可以在逐步遍历整个信号时每次只对几个连续脉冲进行解卷积以减小转速变化的影响,但该过程并没有充分利用信号的全局信息来提高结果的有效性。为充分利用信号的全局信息,本文利用先验转速信息提出用于处理变转速工况下解卷积问题的IMOMEDA方法。
IMOMEDA的关键在于重新构建目标向量t,使其可以随转速变化自适应地调整非零元素的位置。首先,定义v=[v1,v2,…,vN]T为与输入振动信号x相对应的转速信号,单位为r/min,则累计转角可近似计算为
(14)
根据脉冲的故障特征阶次OFCO,角度域脉冲间隔为
Δθ=360/OFCO,
(15)
则角度域中的目标向量可定义为
(16)
式中:fs为转频;K为脉冲总数;θ0为第1个脉冲所在角位移;δ(·)为阶跃函数。
角度域目标向量tn中的非零元素具有周期性,可以通过调整θ0构造一个目标向量来计算最优逆滤波器;但由于离散采样的原因,在tn非零元素点可能没有对应的采样点,因此采用最近的采样点作为近似,将(16)式松弛为
(17)
通过(17)式构造的角度域目标向量tn使多D范数具有较好的突出脉冲的能力。但振动信号是固定时间间隔采样,在角度域上并非等间距,这意味着相邻脉冲之间的采样点数不是常数,因此时域上目标函数Nt可定义为
(18)

在实际应用中,不仅需要提取故障脉冲,更需要对提取的故障脉冲进行度量以作为预测性维护或诊断的依据。在MOMEDA中,将多点峭度作为故障脉冲的度量指标,其定义为
(19)
基于多点峭度的定义,采用故障周期、整数倍周期和分数倍周期构造目标向量同样可以成功提取故障脉冲,多点峭度最大时对应的采样点数可能为故障周期或其整数倍或分数倍,这使得故障脉冲的确切特征阶次难以直接识别。为解决这个问题,本文基于阶次平方包络谱定义包络谐波强度并形成包络谐波强度谱图,以突出信号在角度域的周期性调制,定位主要分量的故障特征阶次。包络谐波强度的表达式为
(20)
式中:AOSEA(O)为阶次平方包络谱在第O阶的幅值;REHIn(O)为前n个幅值的几何平均值。
在包络谐波强度谱图中可以识别到的潜在故障特征阶次为
Od=argmaxREHIn(O),
(21)
当Od接近某个故障特征阶次时,可认为发生了相应故障,从而实现故障特征阶次的自动定位。IMOMEDA方法的具体流程如图1所示。
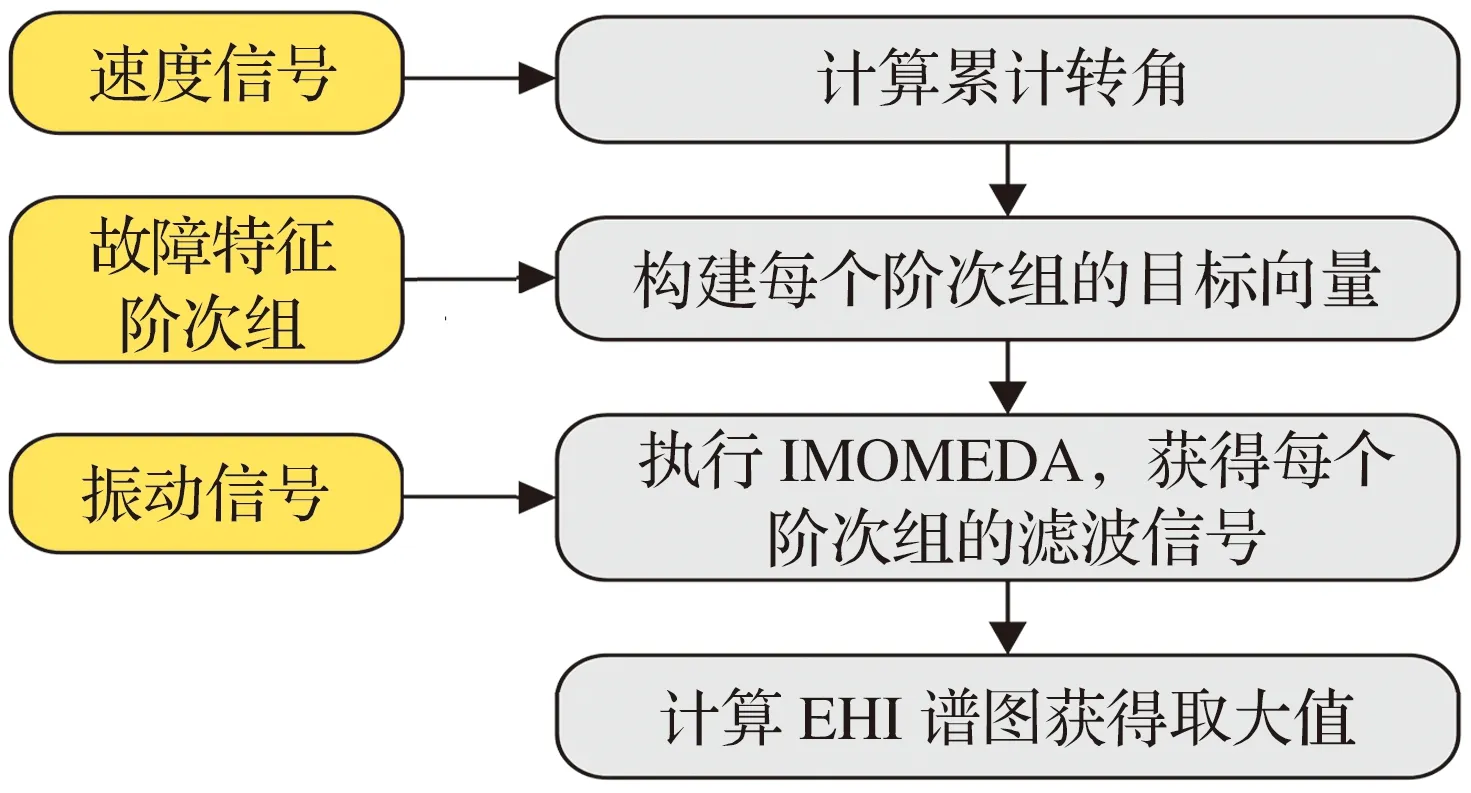
图1 IMOMEDA故障诊断流程
4 仿真结果分析
为评价IMOMEDA方法的性能,通过仿真信号进行研究。仿真信号x(t)由故障冲击信号x1(t)、离散谐波信号x2(t)以及高斯白噪声n(t)组成,即
x(t)=x1(t)+x2(t)+n(t),
(22)
(23)
(24)
(25)
仿真信号中:x1(t)表示滚动轴承故障引起的周期脉冲信号,采样频率为20 kHz,采样时间为1 s;故障脉冲参数A1,A2分别为1,0.25;s(t)为单个脉冲;a为谐振阻尼系数,取500;fn为共振频率,取2 000;Ti为故障脉冲位置;f0(t)为瞬时转速。x2(t)表示来自轴等其他部件的离散谐波信号,该部分假定出现了2个谐波,参数分别为C1=0.2,R1=1以及C2=0.1,R2=20;fk(t)为对应的瞬时频率;高斯白噪声n(t)的标准差为0.4。
为充分说明IMOMEDA方法在时变转速下提取故障特征的能力,采用4种不同的速度曲线(抛物线、线性曲线、指数曲线和余弦曲线)产生信号并进行分析,转速变化曲线如图2所示。将CYCBDang作为对比方法,同时在Intel(R)Core i7-7700K CPU和32GB内存的计算机上运行,数据处理软件为MATLAB R2020a。
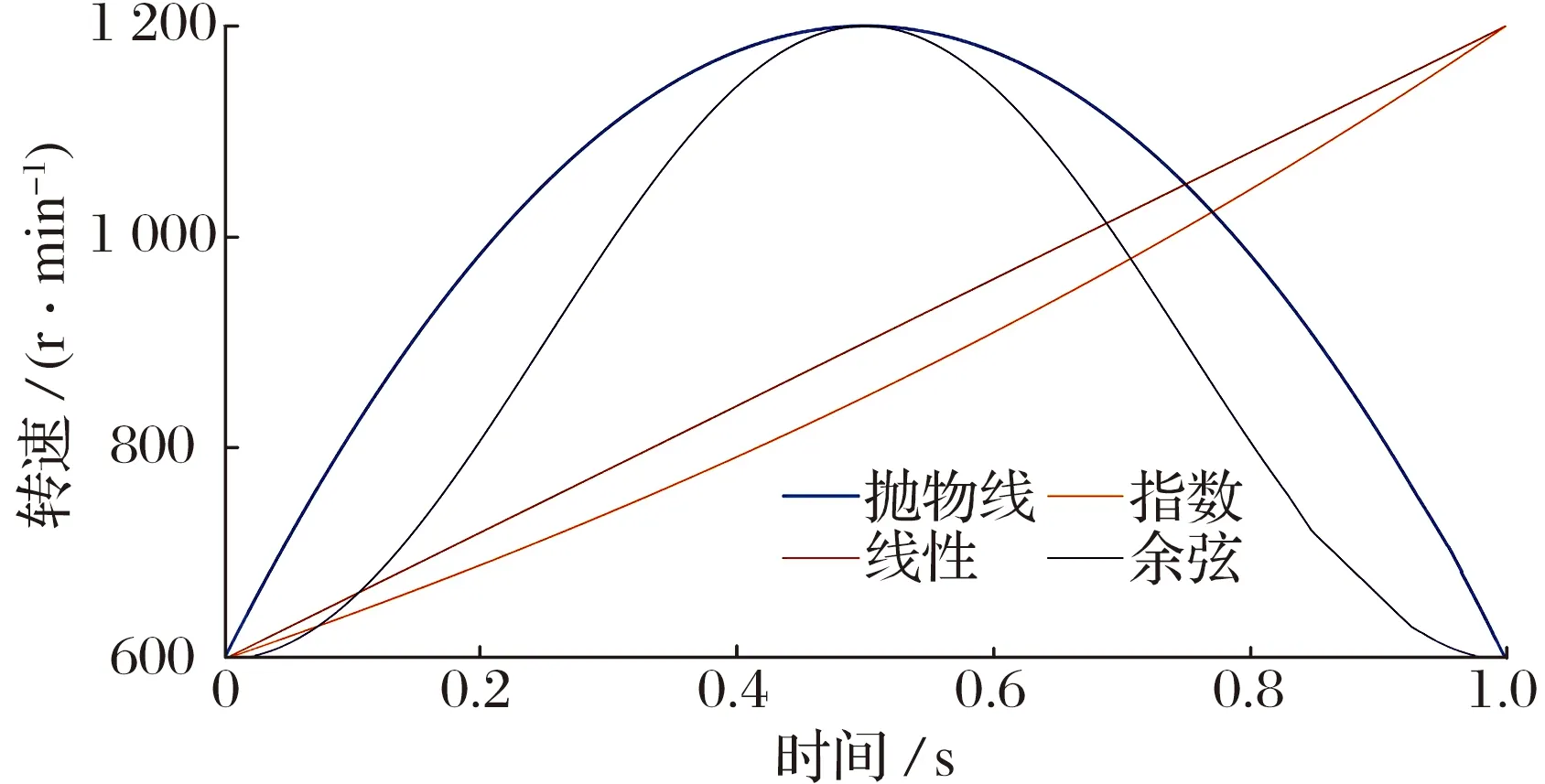
图2 仿真工况转速变化曲线
转速曲线线性变化时模拟信号所含分量的波形如图3所示,循环脉冲相对于转速的阶数设为5。混合后信号中无法观察到循环脉冲,几乎完全被干扰所淹没。
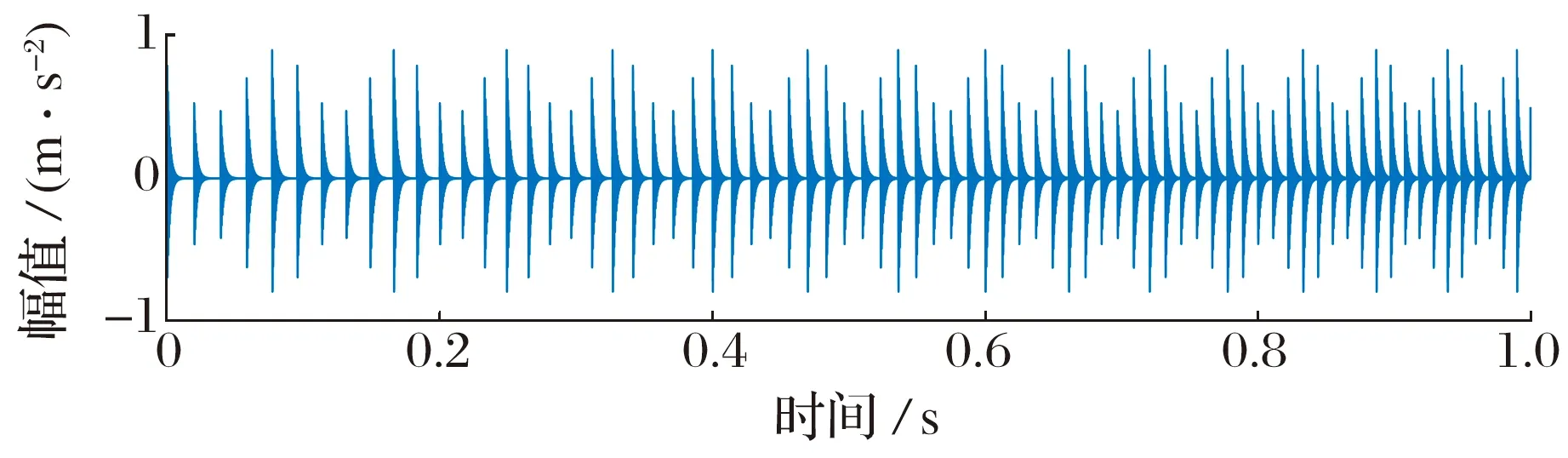
(a) 故障冲击信号
IMOMEDA与CYCBDang在这些信号上的处理时间如图4所示,可以明显看出IMOMEDA的处理时间远小于CYCBDang。CYCBDang需要迭代计算直到得到最优解或局部最优解,而IMOMEDA则无需迭代过程,因此可以在很短的时间内完成。
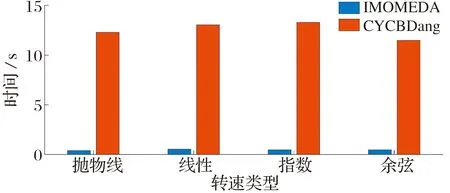
图4 IMOMEDA和CYCBDang的计算时间
4种速度条件下,IMOMEDA和CYCBDang的提取结果如图5所示,2种方法都得到了相似的结果,说明IMOMEDA在提取效率提高的同时不影响其提取效果的有效性。
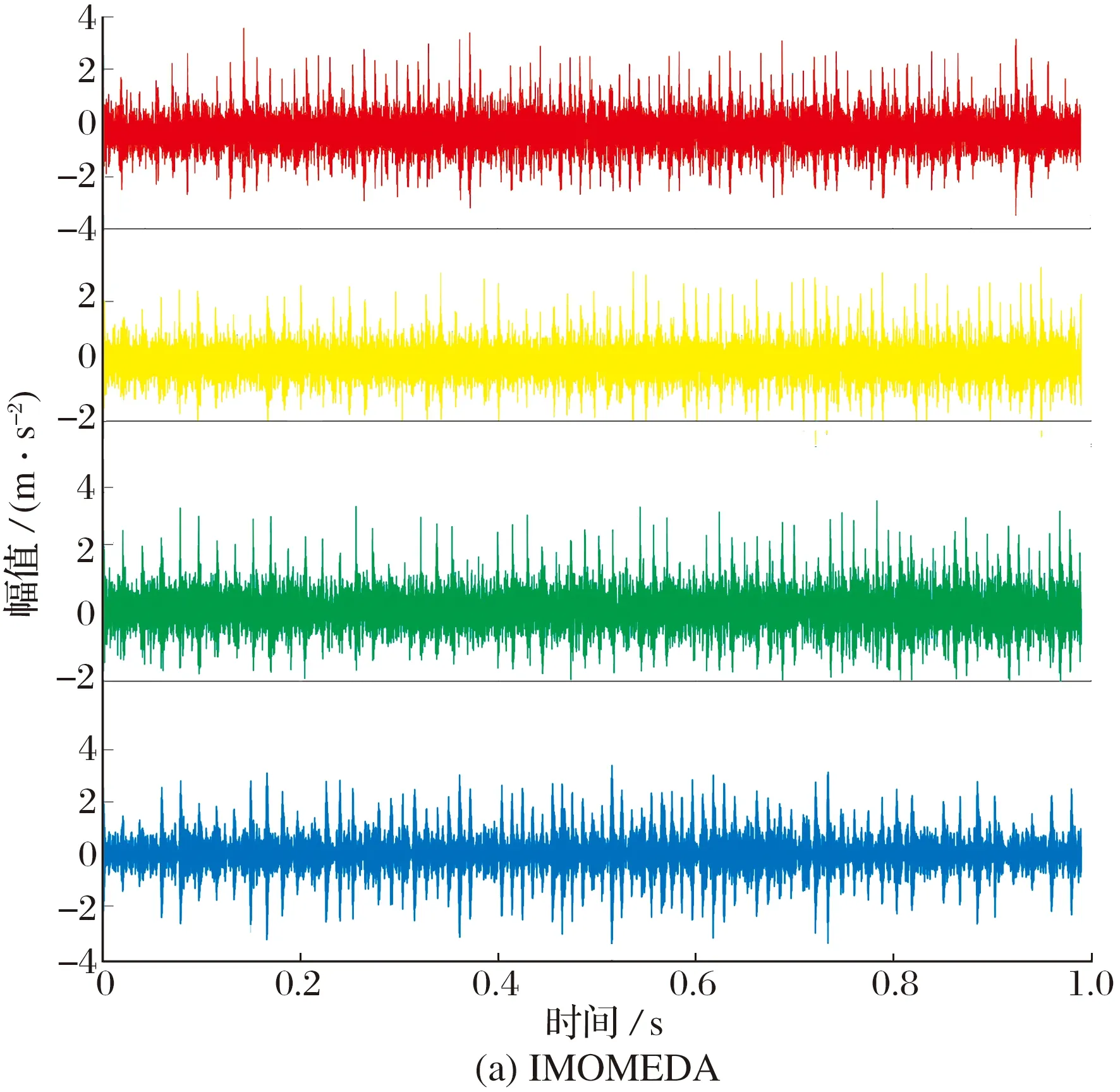
图5 不同方法获得的滤波信号
故障类型的识别是机械设备预测性维护的另一个关键问题。对于MOMEDA,CYCBDang,CYCBD和MCKD等解卷积方法,即使输入的周期/阶次是准确故障周期/阶次的倍数或分数时,仍然可以提取故障特征,但此时输入的周期/阶次也可能对应其他部件的故障,会产生误导。因此,准确识别故障特征的循环频率或阶次至关重要。
MOMEDA采用多点峭度进行故障脉冲的度量,但并不适用于故障脉冲特征阶次的自动定位。不同故障特征阶次信号的多点峭度谱图如图6所示:对于故障特征阶次为10,20的信号,多点峭度难以直接定位故障特征阶次的准确值,在10阶和20阶处均存在明显峰值,甚至在分数倍阶次的5阶处峰值更大,易造成故障特征阶次的误判。

(a) OFCO=10
IMOMEDA处理不同故障特征阶次信号时的包络谐波强度谱图如图7所示:当故障特征阶次为10,20阶时,EHI谱图中最大值对应的阶次同样为10,20阶,并且对应幅值相对于其他阶次更大,不易造成误判。因此,可以直接在包络谐波强度谱图中进行故障特征阶次的定位,且方法简单。
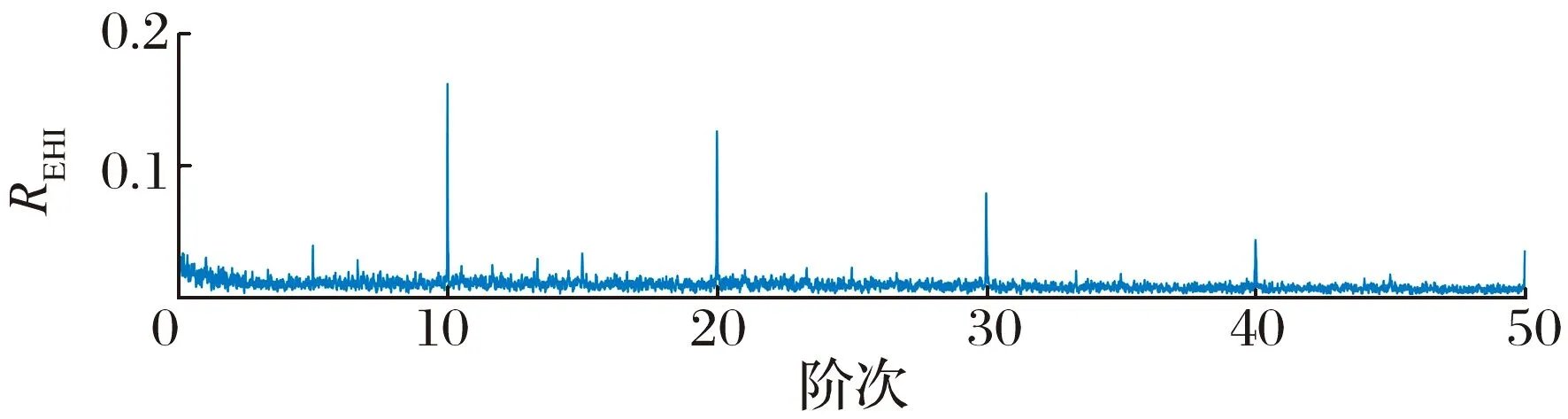
(a) OFCO=10
5 试验验证
在某轨道交通企业的整车滚动综合试验台进行振动测试,试验对象为某型在役走行部轴箱轴承,机车试验台架单次可进行单节车辆的滚动试验,同时搭载8套CRI-2692试验轴承,试验轴承的结构参数及各特征阶次见表1。
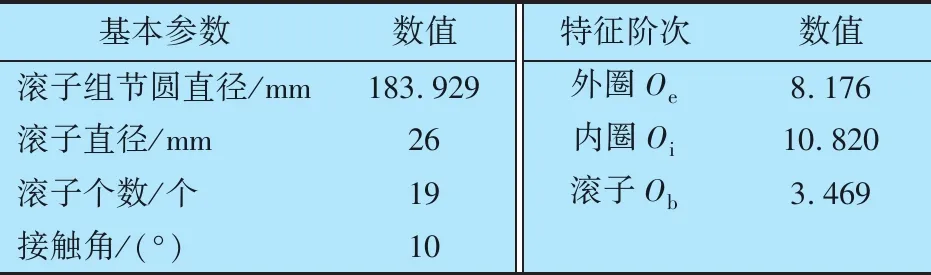
表1 轴承设计参数及各特征阶次
5.1 轴承外圈故障
轴承外圈故障试验信号的采样频率为20 kHz,共采集4 s,实际工况下的转速变化如图8所示,从130 r/min匀减速到73.2 r/min,该过程中采集到的轴承外圈故障信号及其阶次包络谱如图9所示,从时域波形中可以看到部分瞬时脉冲,但在阶次包络谱中难以观察到显著的冲击成分。
将IMOMEDA和CYCBDang的滤波器长度设定为200,处理所得滤波信号如图10所示,IMOMEDA和CYCBDang明显增强了故障脉冲,在阶次包络谱中可以发现显著的冲击成分。另外,IMOMEDA的处理时间为1.91 s,远远小于CYCBDang的194.39 s,在获得相似结果的同时大大提高了处理效率。
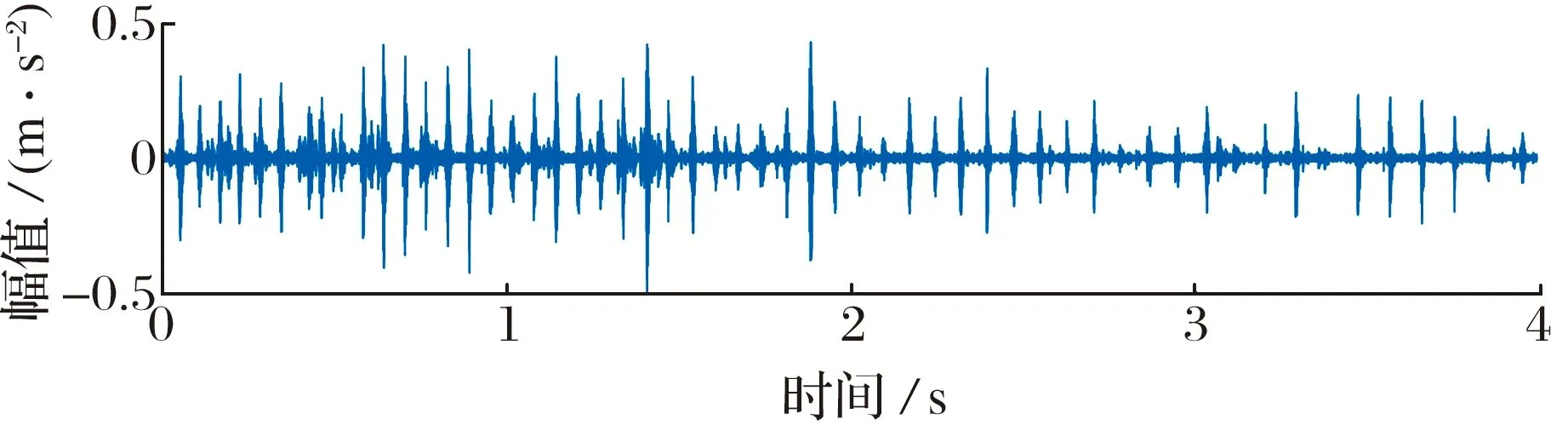
(a) IMOMEDA
IMOMEDA处理时轴承外圈故障信号的包络谐波强度谱图如图11所示,从图中可以明显看到EHI谱图中最大值对应的阶次为外圈故障特征阶次,且峰值远高于其他阶次,可以准确定位故障特征阶次。
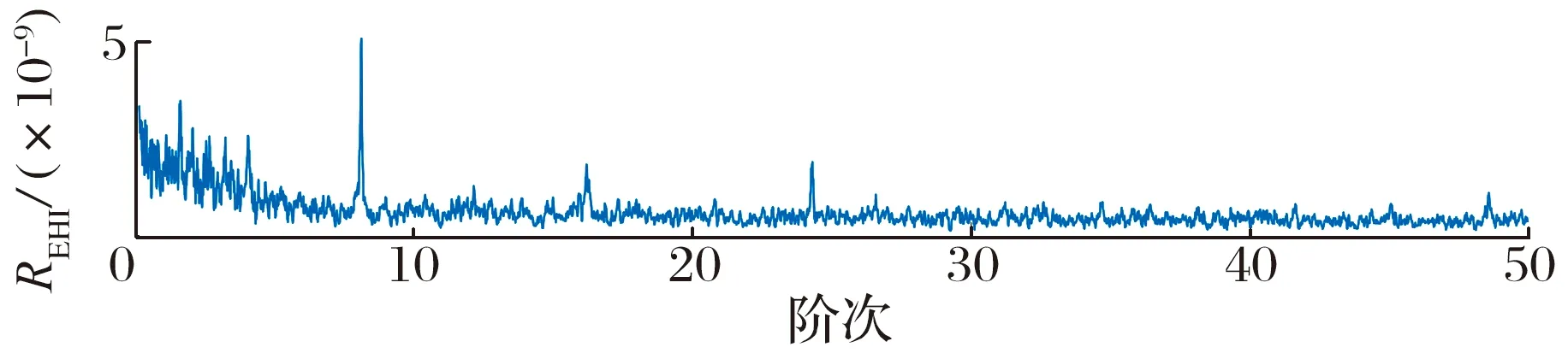
图11 轴承外圈故障滤波信号的包络谐波强度
5.2 轴承滚动体故障
轴承滚动体故障试验信号的采样频率为20 kHz,实际工况下的转速变化如图12所示,从58 r/min匀加速到84 r/min,该过程中采集到的滚动体故障信号及其包络谱如图13所示, 从时域波形中可以看到部分瞬时脉冲,在阶次包络谱中也可以发现部分峰值,但谐波成分仍然不显著。

图12 滚动体故障工况的转速变化曲线
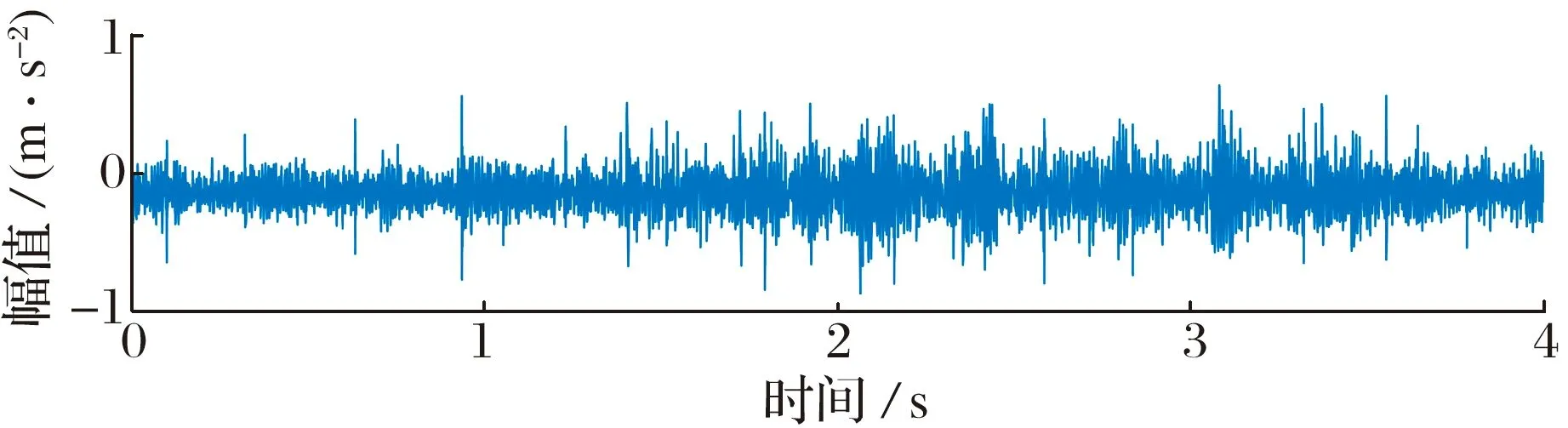
图13 滚动体故障信号及其包络谱
将IMOMEDA和CYCBDang的滤波器长度设定为200,处理所得滤波信号如图14所示,IMOMEDA明显增强了故障脉冲,在阶次包络谱中可以发现显著的峰值及谐波成分,效果优于CYCBDang。CYCBDang的处理时间为192.61 s,而IMOMEDA的处理时间仅为2.64 s,同样大大缩短了处理时间。
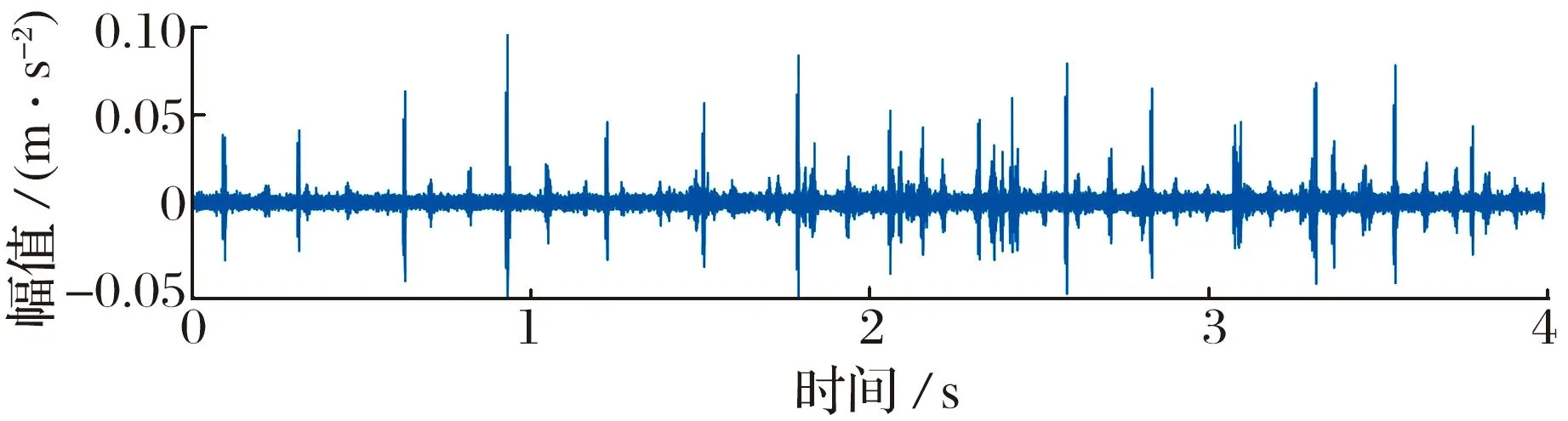
(a) IMOMEDA
IMOMEDA处理时轴承滚动体故障信号的包络谐波强度谱如图15所示,可以明显看到EHI谱图中最大值对应的阶次为滚动体故障特征阶次且峰值高于其他阶次,可以准确定位故障特征阶次。
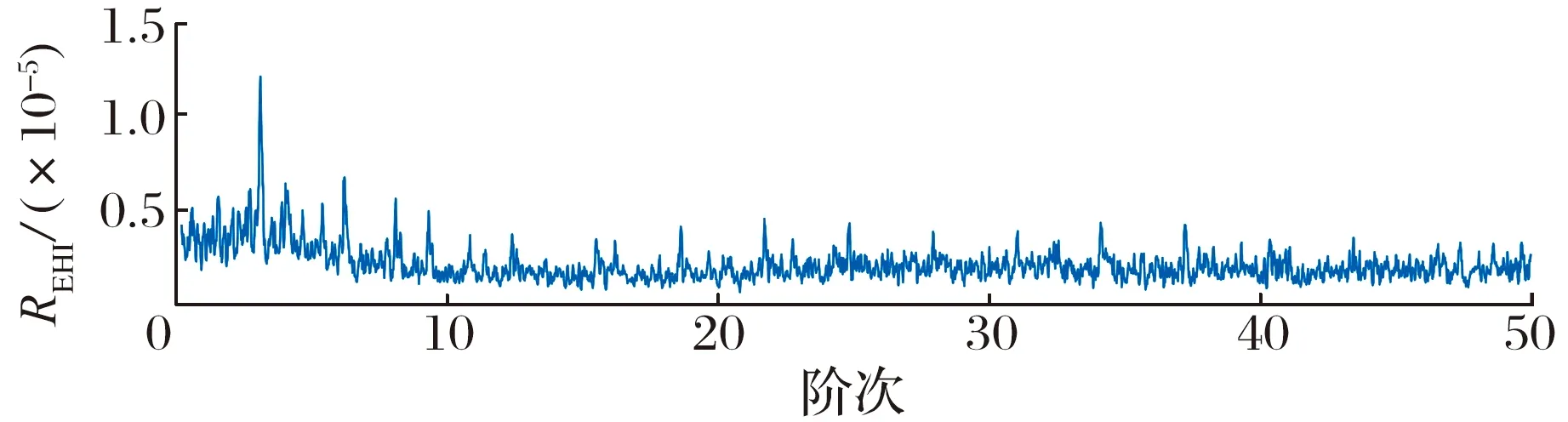
图15 滤波信号的包络谐波强度
6 结论
1)IMOMEDA方法将MOMEDA中以固定间隔的目标向量替换为随转速变化的目标向量,使其获得时变转速条件下的振动信号分析能力。
2)相较于CYCBDang等解卷积方法,IMOMEDA无需进行迭代求解,计算效率更高。
3)基于提出的包络谐波强度可以准确定位故障特征阶次,解决了MOMEDA基于多点峭度而无法识别故障脉冲确切特征阶次的问题。
