基于DR-VAE与自注意力机制的电机轴承故障诊断

2023-09-15杨青刘彦俏吴东升崔宝才

轴承 2023年9期

杨青,刘彦俏,吴东升,崔宝才

(沈阳理工大学自动化与电气工程学院,沈阳 110159)

电机轴承通常在变工况下运行,而且故障数据少且样本不平衡,电机轴承故障诊断精度与泛化能力低。传统轴承故障诊断方法常用数据过采样、欠采样与混合采样等解决故障数据不平衡问题:文献[1]提出了一种基于生成对抗网络不平衡故障诊断方法;文献[2]提出了线性判别分析的欠采样程序并使用灰狼优化算法进行阈值调整;文献[3]提出了将混合采样法与支持向量机相结合的故障诊断方法。然而,过采样由于过多重复正例会造成过拟合,欠采样则会忽略一些反例数据,使用采样方法有过拟合风险且生成样本单一。文献[4]提出了矢量量化变分自编码(Vector Quantised Variational Auto Encoder,VQ-VAE)生成模型,其生成样本具有多样性且质量好,更适用于解决轴承故障诊断中故障数据与正常数据不平衡问题。

针对实际工作中电机轴承变工况导致故障诊断精度低的问题,文献[5]提出了一种子领域自适应的迁移学习故障诊断方法;文献[6]提出基于自适应噪声模态分解和正余弦算法优化多核相关向量机的轴承故障诊断方法:这几种方法都通过自适应迁移学习解决了变工况轴承振动数据特征分布不一致问题。另一种思路是进行多特征融合:文献[7]将卷积神经网络(CNN)和门控循环单元(GRU)时序处理能力的优势结合,提出了一种双通道特征融合CNN-GRU齿轮箱故障诊断方法;文献[8]提出了一种由卷积神经网络实现的变分概率自动编码器框架,在通过编码器前对数据进行融合,然后提取融合特征,融合后的信息包含着空间和频谱信息;文献[9]提出了稀疏滤波网络的电流信号无监督特征学习与融合方法,解决了电流信号特征提取难的问题。

注意力机制来源于人类视觉的研究。文献[10]提出了基于注意力机制的动态加权融合AdaBoost分类器。文献[11]提出了基于注意力机制的多层双向GRU的神经网络轴承故障诊断模型。文献[12]提出了基于特征注意机制的改进多尺度卷积轴承故障诊断模型:注意力机制可以有效提取关键特征信息,提高故障诊断精度。

综上分析可知,基于迁移自适应和特征融合的变工况轴承故障诊断方法仍存在不足:迁移后的模型对目标域以外数据的诊断泛化能力不够,而且耗时适中,不适合实时性强的故障诊断任务;不同工况之间存在分布差异,无法确定符合融合的条件。基于上述需求,本文构建一种新的变工况特征融合轴承故障诊断方法,即通过VQ-VAE对故障数据样本进行增强使数据平衡,并将自注意力机制(Self-Attention Mechanism,SAM)与深度残差变分自编码器 (Deep Resnet-Variational Automatic Encoder,DR-VAE)结合以提取关键特征信息,最后通过DR-VAE-SAM网络提取的故障特征融合形成全局特征,进行故障诊断。

1 理论基础

1.1 VAE

变分自编码(VAE)[13]是一种包含隐变量的生成模型,类似传统自编码器的编码解码过程,其结构如图1所示。给定输入数据xi,编码器计算隐含特征向量zi,解码器根据zi重构xi′,其中μi和σi从编码器网络获得。

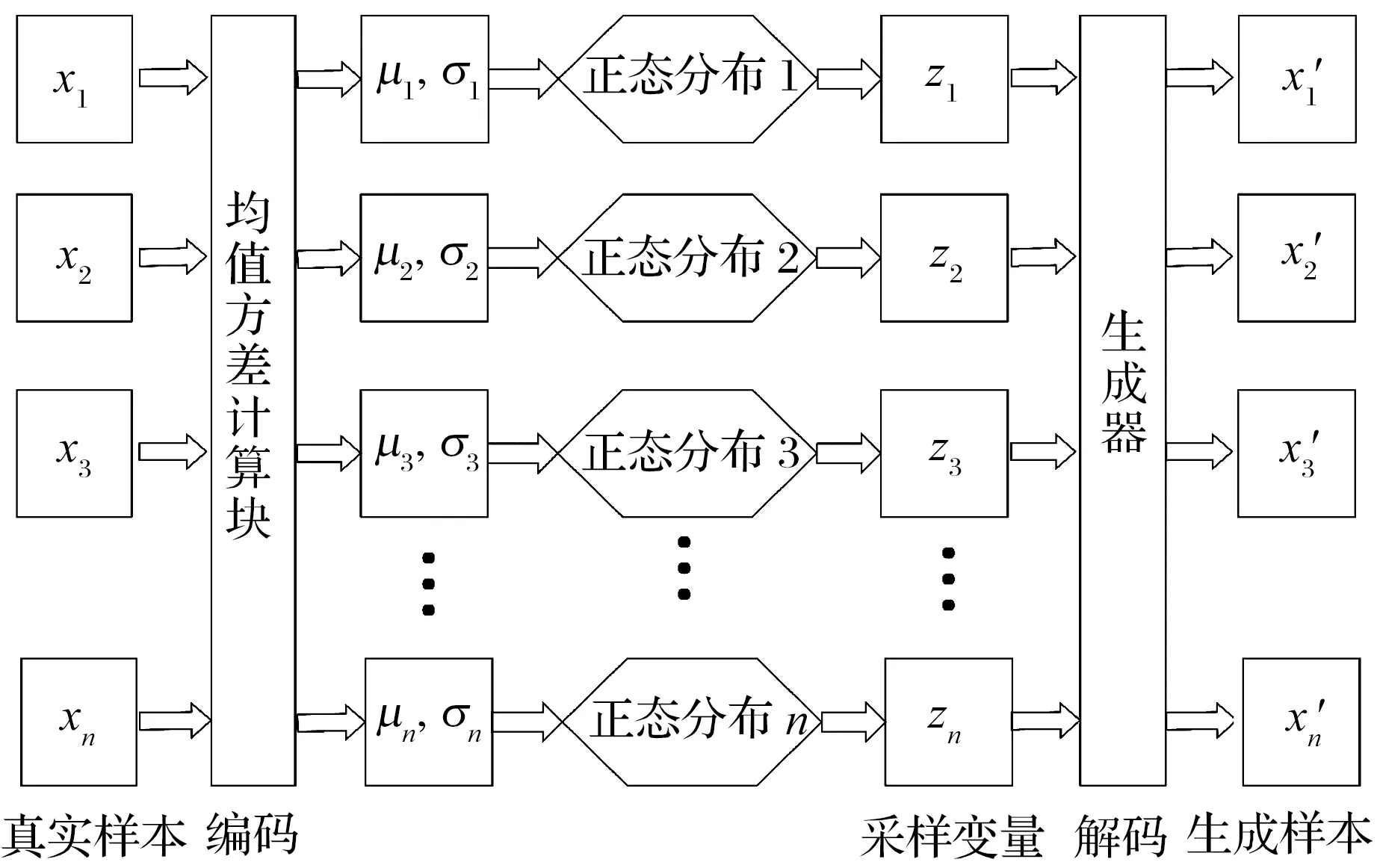
图1 VAE结构图

VAE模型的核心之一是通过最大化变分下界共同训练近似后验模型和生成模型。变分下界的表达式为

E(q)=Ez[logp(x′|z)]-

DKL[q(z|x)‖p(z)]。

(1)

1)最大化Ez[logp(x′︳z)]。灰度图取高斯分布,对数似然为平方差。通过最小化输入数据的重构损失学习编码器和解码器的参数,重构损失的表达式为

(2)

2)最小化DKL[q(z︳x)‖p(z)]。使后验分布近似值q(z︳x)接近先验分布p(z),当q(z︳x)p(z)都是高斯分布时可得

DKL(q(z︳x)‖p(z))=

(3)

式中:zi为单变量高斯分布,由输入数据xi的采样以及参数μi和σi生成。

综上所述,VAE损失函数包括KL散度和重构损耗,可表示为

(4)

1.2 VQ-VAE

VQ-VAE[4]相对于VAE多了一步潜在变量离散化,如图2所示。模型输入x,则通过编码器输出ze(x),为简单起见,将分布q(z︳x)概率定义为one-hot,即

图2 VQ-VAE原理图

(5)

将logp(x)与E(q)绑定,此时q(z=k︳x)是确定的。通过在z上定义简单的均匀先验,获得KL散度常数并等于logk。其总训练目标为

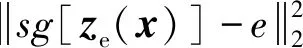
(6)

式中:sg为正向计算时被定义为标识的停止梯度运算符,具有零偏导数。

1.3 DR-VAE

DR-VAE是将深度残差神经网络[14]与VAE结合,利用深度残差编码器提取特征,再由深度残差解码器根据内在分布生成准确的数据。深度残差网络与VAE结合可以提高模型学习性能,避免传统多层神经网络可能出现的梯度消失现象。

在DR-VAE中,深度残差模块由卷积层和直接映射2个部分组成,如图3所示,残差块的表达式为

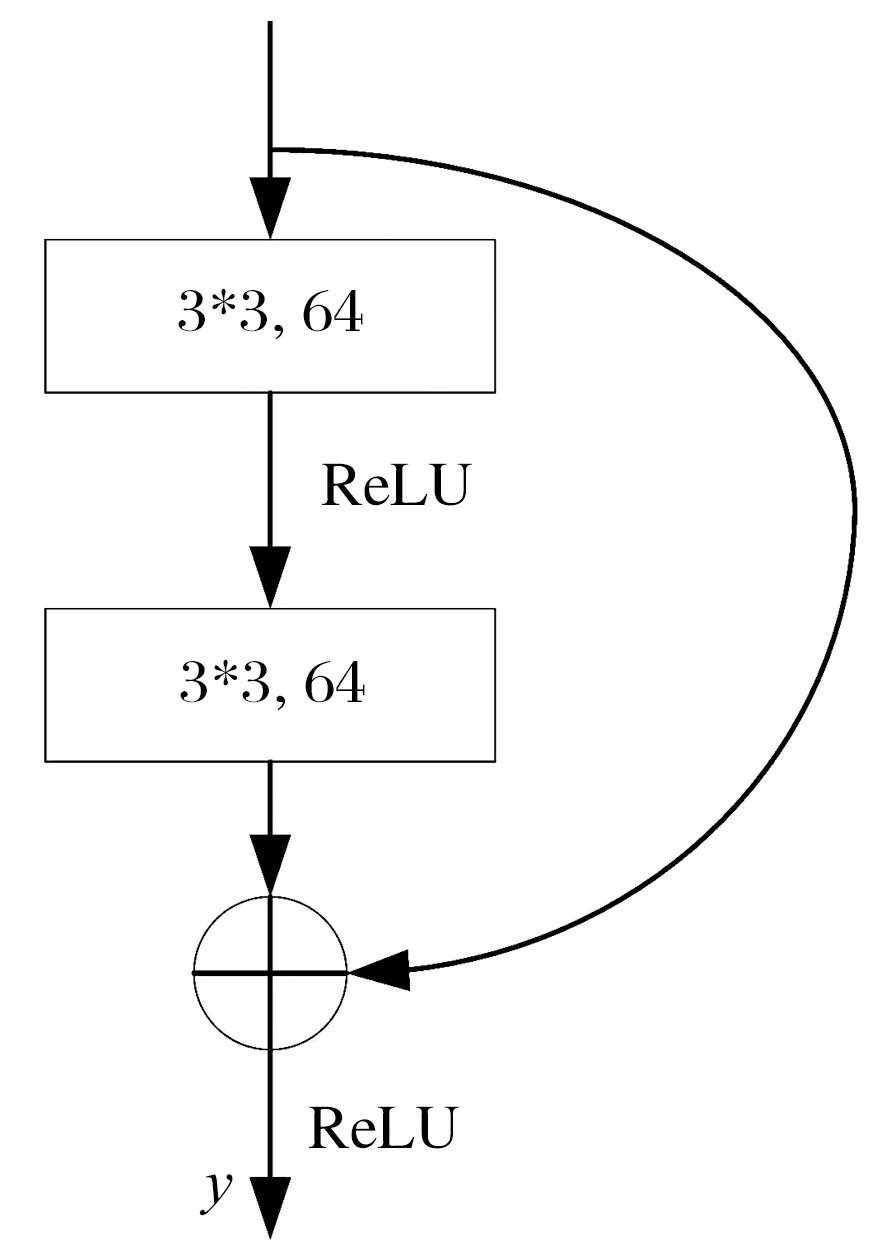
图3 深度残差模块

F(x)=W2σ(W1x),

(7)

y=F(x,{Wi})+x,

(8)

式中:x为残差块的输入;σ为非线性激活函数ReLU;W为神经网络的权重。通过直接映射和第2个ReLU激活函数获得残差块的期望输出y。

DR-VAE可以提取输入数据的隐藏特征,将特征信息融合重构后输入故障分类器进行故障分类。然而,其局限性在于编码器必须将整个信息序列压缩成一个固定长度的向量,造成部分微小故障特征不明显,影响模型测试精度。因此本文在编解码过程中引入自注意力机制,通过神经网络学习隐藏特征的注意力权重,并根据其重要性分配权重(故障相关性高的特征分配高的注意力权重);最后将隐变量及其相应的注意力权重的加权和输入解码器得到更准确的特征,从而在不增加模型参数的情况下提高模型的表达能力,进而提高模型测试精度。

1.4 自注意力机制

自注意机制是注意力机制[15]的一种变体,如图4所示。本质是为输入序列中的每个元素各自分配一个权重系数w,每个元素都以(q,k,v)的形式存储,通过计算学习(q,k)的相似度完成寻址。

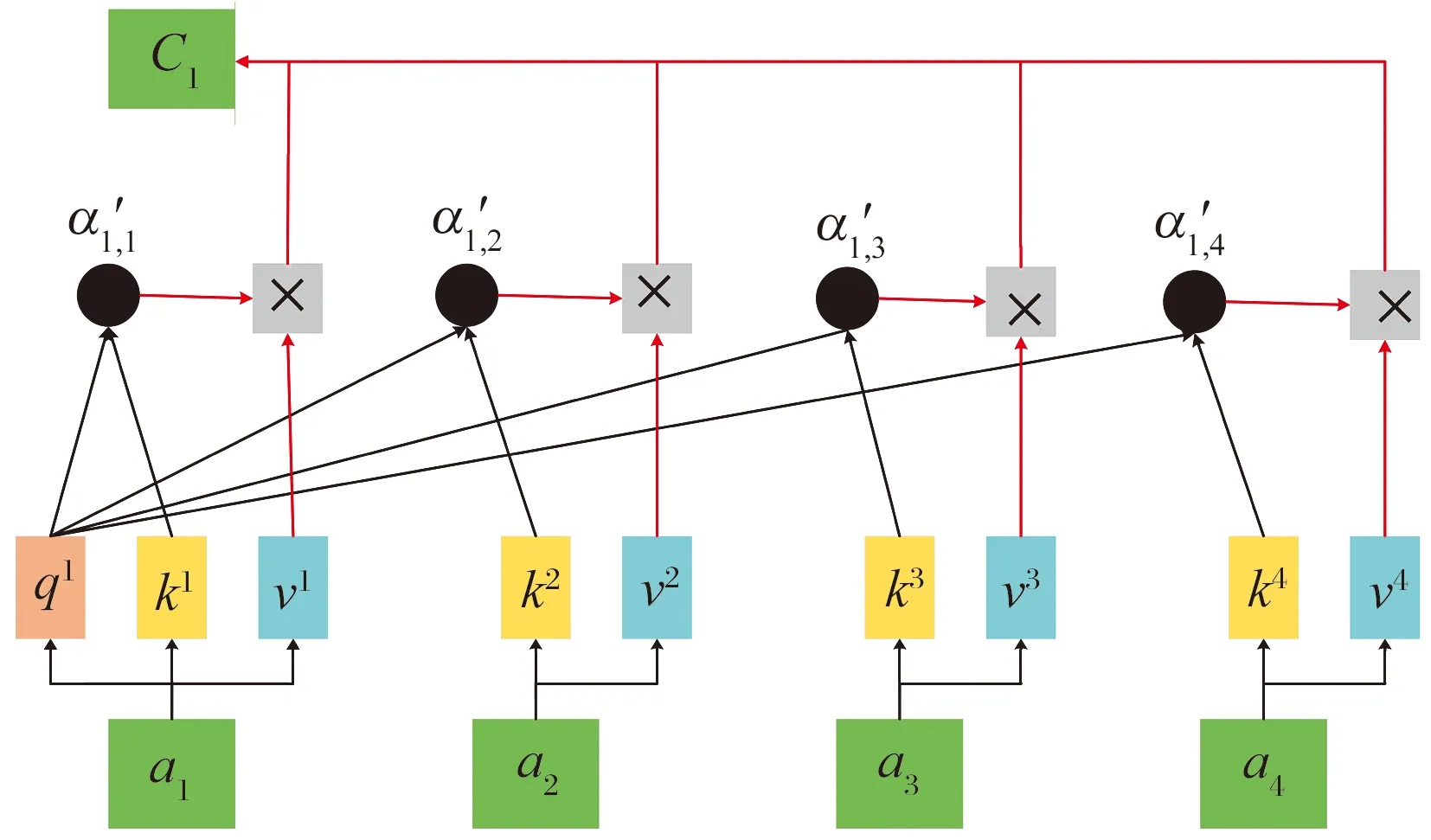
图4 自注意力机制结构图

相似度反映了所提取v值的重要程度,即注意力权重αi,可表示为

αi=sigmoid(kiqi),

(9)

注意力权重可用于构建内容向量c,内容向量cj是隐藏的特征状态ai及其相应注意权重的加权和,即

(10)

每个输出cj不仅依赖ai,还有其他输入的隐藏特征状态,从而找到应该更加关注的输入。

1.5 迁移特征融合

引入迁移学习中的最大均值差异(Maximum Mean Discrepancy,MMD)距离作为衡量各工况之间分布差异的指标,进而判断各工况数据特征融合的难度,从中选取2个MMD距离最小的工况进行数据特征融合并输入训练网络训练,以提高模型特征融合的稳定性。

MMD距离可表示为

(11)

式中:k(*)为将原变量映射到高维空间中的映射函数;X,Y分别为2个工况的数据样本集;x,y分别为2个工况的样本矩阵;F为映射函数集;m,n分别为2个数据集的大小。

2 DR-VAE-SAM网络模型

本文提出的DR-VAE-SAM集合型不平衡变工况轴承故障诊断模型的结构如图5所示:首先,通过VQ-VAE对故障数据样本进行增强,提高训练模型的诊断精度,解决故障数据少和样本不平衡问题;然后,将深度残差网络与变分自编码结合提取故障特征,并使用MMD作为融合标准以提高特征融合的稳定性;最后,引入自注意力机制层提取融合特征的关键信息并输出分类结果。

图5 DR-VAE-SAM结构图

2.1 数据预处理

(12)

本文将原始一维振动信号转化为二维灰度图像,然后通过VQ-VAE模型进行故障数据扩充。

2.2 DR-VAE-SAM轴承故障诊断模型

通过DR-VAE模型提取输入数据xi的隐藏特征zi,再将2种工况的隐藏特征进行融合,得到全局隐藏特征。如图6所示,本文在编解码过程中引入自注意力机制,使模型可以通过神经网络学习注意力权重αi;因此,DR-VAE-SAM模型能够很好地区分不同隐变量的重要性,通过对注意力权重加权突出更多与故障诊断相关的部分。

图6 模型原理图

第i个隐藏特征状态zi获得的注意力权重为

(13)

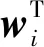
在每个解码器位置j,根据编码器所有隐藏特征状态zi及其相应注意权重的加权和得到状态向量cj,即

(14)

cj不仅依赖zi,还有其他输入的隐藏特征状态,从而找到应该更加关注的隐藏特征状态。

DR-VAE-SAM模型的损失函数包括残差网络中均方损失函数L1与VAE损失函数LVAE,分别为

L1=(x1-yi)2+(x2-yi)2,

(15)

(16)

式中:μi,σi为从编码器网络获得的均值方差参数;x1,x2分别为参与融合的工况1和工况2数据。

2.3 基于DR-VAE-SAM的轴承故障诊断流程

DR-VAE-SAM轴承故障诊断模型可分为数据预处理、数据集平衡、离线阶段、在线阶段4个部分,其具体流程如图7所示:

图7 诊断流程图

1)将采集的数据转化为灰度图,通过VQ-VAE处理不平衡的数据并计算各数据集之间的MMD距离,选择MMD距离最小的数据集。

2)在历史数据离线建模阶段,通过深度残差编码器对输入数据进行特征提取。

3)将需要融合的数据特征进行融合。

4)引入自注意机制层,根据融合后的特征信息对特征进行加权,提高模型特征提取能力。

5)将深度残差解码器解码后的特征输入GMM故障分类器进行分类,并根据注意力权重计算联合重构损失和VAE损失,通过反向传播更新网络参数,直到迭代结束,保存得到的模型。

6)在工厂数据在线诊断阶段,采集在线数据,将采集到的数据转化为灰度图,输入到保存好的模型中,进行在线故障诊断并输出诊断结果。

3 试验验证

为验证DR-VAE-SAM轴承故障诊断模型的有效性和准确性,利用美国凯斯西储大学(CWRU)和东南大学的轴承数据集进行验证。试验环境配置采用的CPU为Intel Core i7-8700,GPU为NVIDIA GTX 1080 Ti,深度学习框架为Pytorch,模型的主干网络为Resnet18。模型初始状态的学习率为0.001,动量因子的值调整为0.8,批训练大小为64,epoch为50;模型采用适合轴承数据的AdamW优化器,其对内存需求小,同时能够减小损失,加快找到最优参数并得到目标函数最优解,学习率设置为0.001,衰减率为10-8。

3.1 CWRU轴承数据

3.1.1 数据预处理

本试验采用CWRU轴承数据集[16]中48 kHz采样频率下的轴承数据,试验轴承型号为6205,按照其转速分为A,B,C这3类工况,每类工况包含1种正常数据和9种故障数据。故障数据分别由内圈(IR)、外圈(OR)、钢球(B)各3种损伤程度组成(损伤直径分别为0.178,0.356,0.534 mm)。

在原始一维振动信号的基础上,将其转化为二维灰度图像,以A工况为例,转换后的灰度图如图8所示,根据试验要求利用VQ-VAE模型扩充故障数据至满足要求(正常数据无需扩充)。其中,0.534OR故障数据的灰度图如图9所示,VQ-VAE生成故障的图像特征比原始故障明显。VQ-VAE生成的数据样本不仅保留了原输入数据的特征,而且在其基础上对相关特征数据进行了增强处理,解决了数据不平衡问题。

(a) 原始故障数据

(a) 真实样本 (b) VQ-VAE生成样本

本试验在每类工况下采集10种故障的真实数据各115条,扩充数据85条,即每种故障数据有200条,最终得到的训练集包括6 000张真实数据和扩充数据的二维灰度图,每类工况各2 000张;训练集与测试集的比例为4∶1,即每个测试集中包含一个工况真实数据二维灰度图500张。

3.1.2 MMD距离计算

计算各工况数据之间的MMD距离,为尽可能地增强融合效果,降低融合难度,提高模型稳定性,选择MMD距离最小的2个工况数据进行特征融合。根据表1,本模型选择融合工况A和工况B的数据特征并完成模型训练。

表1 MMD距离统计表

3.2 数据不平衡试验

为进一步验证VQ-VAE模型解决故障诊断中数据不平衡问题的有效性,本文用VGG,ResNet,AleXNet,GoogLeNet模型对不同工况的原始数据和增强数据分别进行试验,结果如图10所示,对比可知,通过VQ-VAE模型增强后数据训练出的模型的故障诊断准确率更高。深度学习网络训练通常需要大量的数据,故障样本过少时模型会过拟合,从而影响模型诊断精度;因此,通过VQ-VAE进行数据增强可以有效提高故障诊断精度。

图10 原始数据与增强数据试验对比图

ResNet使用增强数据对工况A,B,C的故障诊断准确率分别为98.5%,99.0%和95.5%,比其他模型高0.2%～4.0%。ResNet也可以解决多层神经网络可能出现的梯度消失问题,从而深度提取数据特征。因此本文选择ResNet作为基础网络架构。

3.3 变工况试验

为验证DR-VAE-SAM变工况故障诊断方法的有效性,设置9个试验任务,试验结果取平稳阶段的平均准确率,由表2可知:

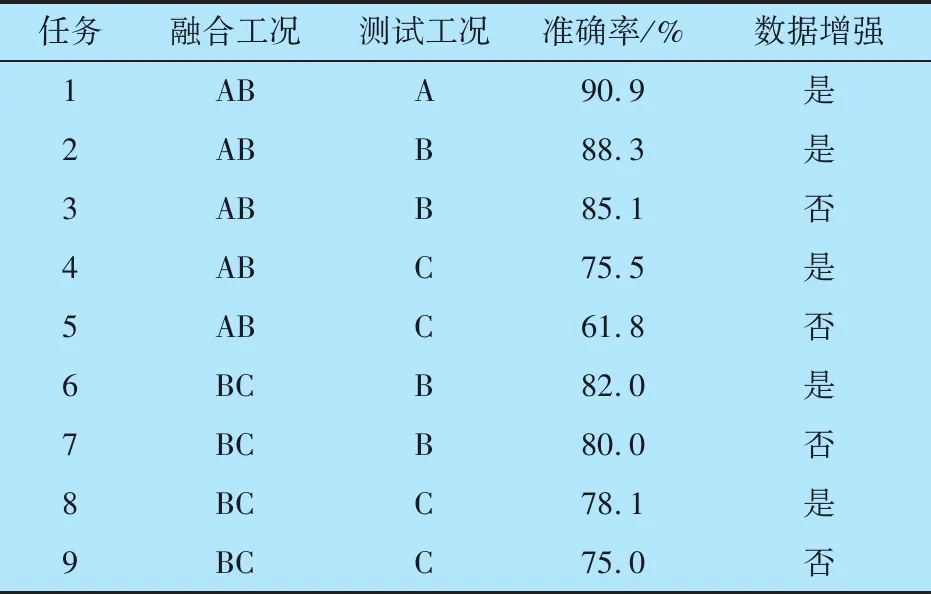
表2 变工况试验的准确率

1)任务1,2,4,6,8利用增强数据训练可以提高故障诊断准确率。

2)任务1,2的准确率高于任务4。这是由于任务1,2测试的是参与融合的工况,而任务4测试的是未参与融合的工况,数据特征无法完全表示,具有局限性,因此诊断精度有一定幅度的下降。

3)任务1,2准确率高于任务6,8。这是由于任务1,2选择融合的工况为MMD距离最小的AB工况,融合效果较好。

测试结果表明,DR-VAE-SAM模型具有一定的泛化能力,对未参与融合的数据仍有一定的诊断能力,可以满足变工况故障诊断的要求。

3.4 对比分析

3.4.1 对比模型的选择

目前,变工况轴承故障诊断主要思想是将不同工况分为源域和目标域,使用MMD或Coral等作为特征分布度量准则,利用深度神经网络的可迁移性进行特征空间的变换。深度适配网络(Deep Adaptation Netowrk,DAN)与Deepcoral是经典的迁移学习方法。DAN采用多核MMD减小域差异,从而增强网络具体任务层的特征迁移能力;Deepcoral提出一个coral loss,通过线性变换将源域与目标域分布的二阶统计特征进行对齐。

为验证DR-VAE-SAM模型在变工况轴承故障诊断方面的有效性,将其与DAN,Deepcoral迁移学习模型进行对比,为保证对比试验的有效性、合理性以及全面性,采用控制变量法,即测试数据集和迭代次数一致,环境配置均相同,均采用Pytorch框架训练算法。

3.4.2 对比试验结果

8组对比试验及准确率结果见表3:与变工况试验结果类似,使用VQ-VAE进行数据增强后,DAN,Deepcoral均取得了比原始数据训练更高的的故障诊断准确率,进一步证明VQ-VAE可以提高模型的诊断精度。

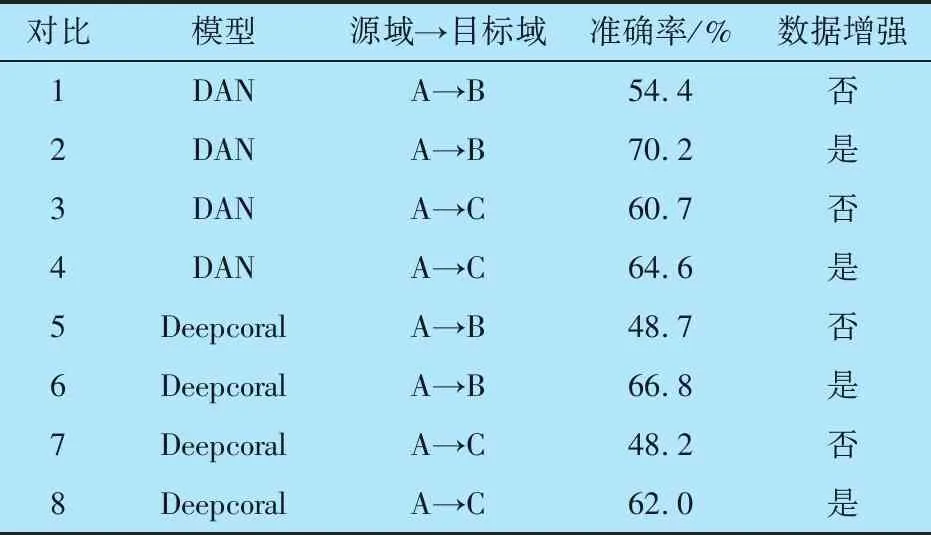
表3 对比试验结果

9组任务和8组对比的结果均证明了数据增强模块的有效性,对于表2和表3种数据增强后的试验结果:DR-VAE-SAM模型对于AB→B,AB→C的准确率分别为88.3%和75.5%,对于BC→B,BC→C的准确率分别为82.0%和78.1%,与DAN和Deepcoral变工况故障诊断模型对A→B和A→C工况的准确率分别高出4.1%,1.5%,4.7%和2.9%,证明了特征融合模块的性能。

综上,迁移学习虽然在一定程度上解决了变工况数据分布差异的问题,但仍可能出现特征空间转换的误差,导致特征分布无法完全匹配,从而降低变工况轴承故障诊断的精度。本文模型通过特征融合和自注意力机制,使故障特征具有区分性和代表性,能更有效地表达轴承故障数据的本质特征,提高故障诊断的精度和泛化能力。总体而言,DR-VAE-SAM模型在数据不平衡和变工况故障诊断方面都略优于其他方法。

3.5 泛化性试验

3.5.1 东南大学试验数据

采用东南大学变速箱数据集[17]中的轴承数据进行DR-VAE-SAM模型的泛化能力试验。本试验采用通道2的数据,包括正常、钢球故障、外圈故障和内外圈复合故障,每种故障选取200个样本,按照2∶1的比例划分训练集和测试集。选取转速-负载配置为20 Hz-0 V的数据为工况D,30 Hz-2 V的数据为工况E。

3.5.2 试验结果

将DE工况融合后训练模型。设置2个任务,进行4组对比试验。任务一,使用工况D的500张真实数据二维灰度图作为测试工况并输出结果;任务二,使用工况E的500张真实数据二维灰度图作为测试工况并输出结果。2个任务均在本试验训练好的模型上测试。2组对比分别用DAN,Deepcoral进行工况D→E和E→D的试验,其中,源域为有标签的训练样本,目标域为无标签的测试样本。试验测试结果见表4。

表4 泛化试验结果

由表4可知,DAN,Deepcoral模型的故障诊断准确率均低于DR-VAE-SAM模型。迁移学习虽然可以解决变工况中源域与目标域数据分布差异问题,但迁移后的模型对于目标域以外数据的诊断仍具有局限性;而本文所提方法可以通过不同工况之间特征融合提取全局特征,使模型具有更强的泛化能力,故障诊断精度更高。