商环的McCoy性

宦明蕾，程 智

（安徽师范大学 数学与统计学院，安徽 芜湖，241003）

引言

设R是一个有单位元的环，I是R的一个理想。R[x]表示环R上的多项式环。

1942 年，McCoy 在[1］中证明了在交换环R中，若f(x)是R[x]的一个零因子，其中R[x]是环R上的多项式环，则R中一定存在一个非零元素把f(x)零化。1997 年，Rege，Chhawchharia[2］和Nielsen[3］分别介绍了McCoy 环的概念。若对任意的非零多项式f(x)=都存在非零元素r∈R使得f(x)r=0，则称R为右McCoy 环。他们讨论了McCoy 环和其他环之间的关系。2008 年，Nielsen 在[4］中对McCoy 环的性质以及McCoy 环和其他环之间的关系展开了深入研究。证明了McCoy 环的直和、直积仍然是McCoy 环，2007 年，雷震在[5］中给出了McCoy 环的一些等价刻画。2013 年，Camillo，Tai 和Lee 在[6］中介绍了右幂零系数McCoy 环（简称NC-McCoy 环），若多项式，那么意味着存在一个非零元素r∈R使得f(x)r∈N(R)[x]（N(R)是R的幂零元集）。受[6］的启发，Mohammad，Sahebi 和Javadi 在[7］中研究了一个广义的NC-McCoy 环。一个环R被称为右J-McCoy 的若对任意两个非零多项式f(x)=满足f(x)g(x)=0，意味着存在一个非零元素r∈R使得air∈J(R)。J(R)是所有极大理想的交。2021 年，程智，吴晶晶等在[8］中证明，如果一个有限维代数的商代数是截断代数，那么该代数是McCoy 环的充分必要条件是该代数对应的箭图没有源点和汇点。

本文在[9］的基础上，介绍了与理想I有关的商McCoy环的概念，给出了商McCoy环的一些性质，并且讨论商McCoy环和其他环之间的关系，文中代数相关概念参见[10-11］。

1 商McCoy环

定义1.1设R为有单位元的环，I是R的一个理想。若对任意的多项式f(x)

满足f(x)g(x)∈I[x]，都存在一个元素r ∈RI使得f(x)r=0，则称R为与理想I有关的右商McCoy 环。类似地，可以定义与理想I有关的左商McCoy 环。若环R既是与理想I有关的左商McCoy环，又是与理想I有关的右商McCoy环，则称环R为与理想I有关的商McCoy环。此外，称R为商McCoy环，是指环R是与任意一个理想I有关的商McCoy环。

接下来用例1.2证明一个与理想I有关的商McCoy环的存在性。

例1.2设R=ℤ6并且I=()是R的一个理想。那么环R是一个与子环I=()有关的右商McCoy环。

证明 对于任意的多项式f(x)∈R[x]，g(x)∈R[x]I[x]，若f(x)g(x)∈I[x]，那么存在一个元素r=使得f(x)r=。故R是一个与子环I=()有关的右商McCoy环。

众所周知，交换环都是McCoy环，但交换环未必是商McCoy环（见例1.3）。

例1.3设R=ℤ4并且I=()是R的一个理想。那么环R不是一个与子模I=()有关的右商McCoy环。

证明 设f(x)=+x，g(x)=+x，显然f(x)g(x)∈I[x]。然而f(x)r=意味着r=或r=，而，都在I中。因此环R不是一个与子模I=()有关的右商McCoy环。

对于一个非交换环R，它可能是一个与理想I有关的商McCoy环（见例1.4）。

例1.4设R=AQ J3，其中Q= (Q0,Q1)是下面的箭图：

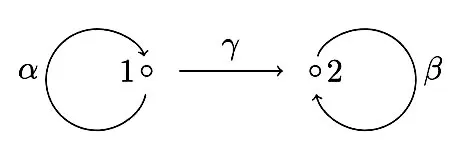
J3是由所有长度为3的路径生成的容许理想。令I是由αγ和γβ生成的R的一个子环。

那么对任意的f(x)∈R[x]，g(x)∈R[x]I[x]，如果f(x)g(x)∈I[x]，g(x)∉I[x]意味着存在一个元素r为α2或者β2使得f(x)r=0。

因此R是一个与子环I有关的右商McCoy环。

并且通过[10，Example2.5］，可以发现一个非交换环可能不是一个商McCoy环。

命题1.5如果R是一个与理想I有关的右商McCoy环，那么R/I是一个右McCoy环。

证明对任意的非零多项式f(x)=那 么 满 足f′(x)g′(x)∈I[x]。由于R是一个与理想I有关的右商McCoy 环，那么存在一个元素r′∈RI使得f′(x)r′=0。故存在一个非零元素r=r′+I∈R/I使得f(x)r=。

因此，R/I是一个右McCoy环。

设R=Ri是环的直积并且I是R的一个理想。显然，I=Ii。其中Ii是Ri的理想，i=1，2，…，n。

定理1.6环R=Ri是一个与理想I有关的右（左）商McCoy环当且仅当Ri是一个与理想Ii有关的右（左）商McCoy环，i=1，2，…，n。

证明 先证明必要性，假设f1(x)g1(x)∈I1[x]成立对多项式f1(x)∈R1[x]，g1(x)∈R1[x]I1[x]。令f(x)=(f1(x),1,…,1)且g(x)=(g1(x),0,…,0)。显然f(x)g(x)∈I[x]并且g(x)∉I[x]。那么存在一个元素r=(r1,r2,…,rn)∈RI使得f(x)r=0。元素r=(r1,r2,…,rn)∉I=I1×I2×…In，表明r1∉I1。

因此f1(x)r1=0 并且R1是一个与理想I1有关的右商McCoy 环。类似地，当i=2,3,…,n时，Ri是一个与理想Ii有关的右商McCoy环。

再证明充分性，对任意的f(x)=(f1(x),f2(x),…,fn(x))∈R[x]，g(x)=(g1(x),g2(x),…,gn(x))∈R[x]I[x] 满 足f(x)g(x)∈I[x]，其 中fi(x),gi(x)∈Ri[x] 当i=1,2,…,n时。 那 么，当i=1,2,…,n时，fi(x)gi(x)∈Ii[x]。

多项式g(x)∉I[x]意味着gi(x)∉Ii[x]对某个下标i∈[0,n]，那么存在ri∈RiIi使得fi(x)ri=0。因此存在r=(r1,r2,…,rn)∈RI使得f(x)r=0。并且当i=1,2,…,n时，若gi(x)∈Ii[x]则ri∈Ii。故R是一个与理想I有关的右商McCoy环。

若Ri是一个环且Ii是Ri的一个理想对于i=1,2,…,n，那么

推论1.7当i=1,2,…,n时，若Ri是一个与理想Ii有关的右（左）商McCoy 环，那么是一个右（左）McCoy环。

现在回忆一下中国剩余定理。

设R是有单位元的环，I1,I2,…,In是R的理想。并且当i ≠j 时，Ii+Ij=R。则存在一个环同构

定理1.8设R是有单位元的环，Ii是R的一个理想，其中i=1，2，…，n。若R是一个与理想Ii有关的右（左）商McCoy环，则R是一个与理想有关的右（左）商McCoy环。

当1≤i ≠j ≤n满足Ii+Ij=R时，反之成立。

证明 对任意的f(x)∈R[x]，g(x)∈R[x]I[x]，若f(x)g(x)∈[x]，则f(x)g(x)∈Ii[x]并且存在ri∈RiIi使得f(x)ri=0。此外有关的右商McCoy环。

相反地，若Ii+Ij=R，其中1 ≤i ≠j ≤n 时，根据中国剩余定理根据推论1.7，是一个右McCoy环。因此，当i=1,2,…,n时，R是一个与理想Ii有关的右商McCoy环。

定理1.9设R是一个环，I是R的一个理想。那么R是一个与子模I有关的商McCoy 环当且仅当R[x]是一个与子模I[x]有关的商McCoy环。

证明 先证明必要性。假设R是一个与子模I有关的商McCoy环。

设F(y),G(y)∈R[x][y]I[x][y] 满足F(y)G(y)∈I[x][y]。此时F(y)=f0(x)+f1(x)y+…+

设k=max{pi+qj+1}。其中fi的次数和F(xk)中多项式的次数一样，gj的次数和G(xk) 中多项式的次数一样。因为F(y)G(y)∈I[x][y]，于是F(xk)G(xk)∈I[x]。因为R是一个与子模I有关的商McCoy 环，那么就存在元素u,v ∈RI使得F(xk)u=0，vG(xk)=0。

因此F(y)u=0并且vG(y)=0。也就是说，R[x]是一个与子模I[x]有关的商McCoy环。

再证充分性，设f(x)=满足f(x)g(x)∈I[x]。

因此，R是一个与子模I有关的商McCoy环。

命题1.10设R是一个与子模I有关的右商McCoy环并且Δ是R的一个由R的中心正则元组成的乘法封闭的子集。那么Δ-1I是Δ-1R的一个理想并且Δ-1R是一个与理想Δ-1I有关的右商McCoy环。

证明首先易证Δ-1I是Δ-1R的一个理想。

设f(x)其中αi,βi∈Δ-1R。那么可以设αi=对于任意的ai,bj∈R，u,v ∈Δ。

现在假设f(x)g(x)∈Δ-1I[x]，设f1(x)因为Δ是R的一个由中心正则元组成的乘法封闭的子集，故f1(x)g1(x)∈I[x]。由于R是一个与子模I有关的右商Mc-Coy环。因此存在一个元素r∈RI使得f1(x)r=0。因为r=∈Δ-1RΔ-1I所以f(x)r=0。因此Δ-1R是一个与理想Δ-1I有关的右商McCoy环。

在x中的Laurant多项式环，系数在环R中，由所有的形式和组成并且有明显的加法和乘法，其中ai∈R并且k,n都是整数。表示为R[x,x-1]，R[x,x-1]的理想可以用I[x,x-1]表示。

推论1.11设R是一个环，I是R的一个理想。若R[x]是一个与子环I[x]有关的右商McCoy 环，那么R[x,x-1]是一个与理想I[x,x-1]有关的右商McCoy环。

证明设Δ={ 1,x,x2,... }，那么Δ是一个由R[x]的中心正则元组成的乘法封闭的子集。因此R [ x,x-1]=Δ-1R[x]，显然R[x,x-1]是一个与理想I[x,x-1]有关的右商McCoy环。

回顾一下，一个环R称为abelian的，如果它的每一个幂等元都是中心的。

命题1.12设R是一个与理想I有关的右商McCoy环并且e是R中的一个幂等元。那么eRe是一个与理想eIe有关的右商McCoy环。如果R是一个abelian环，则反之成立。

证明设f(x)=满足f(x)g(x)∈(eIe)[x]。由于R是一个与理想I有关的右商McCoy 环并且eRe ∈R，eIe ∈I。故存在一个元素r∈RI使得(eaie)r=0。因为eRe={ere|r∈R}并且eIe={eie|i∈I}，故ere ∈eReeIe并且满足(eaie)(ere)=0。

因此，eRe是一个与理想eIe有关的右商McCoy环。

反过来，假设eRe是一个与理想eIe有关的右商McCoy 环。假设f(x)=满足f(x)g(x)∈I[x]。显然ef(x)e ∈(eRe)[x]，eg(x)e ∈(eRe)[x](eIe)[x]。并且根据R是一个abelian 环可以得到(ef(x)e)(eg(x)e)∈(eIe)[x]。那么存在一个元素ere ∈eReeIe使得(eaie)(ere)=eaire=0。因此air=0。

因此R是一个与理想I有关的右商McCoy环。

设α:R→R是一个环的自同态，一个斜多项式环R[x,α]是给R上的多项式环加上新的乘法xr=α(r)x得到的环，其中r∈R。对于环R[x,α]/(xn)，我们总是考虑n ≥2。并且R[x,α]/(xn)的理想可以写成I[x,α]/(xn)，其中I是R的一个理想。

命题1.13设R是一个环且I是R的一个理想。α是R的一个环自同态。则R是一个与理想I有关的右商McCoy环当且仅当R[x,α]/(xn)是一个与理想I[x,α]/(xn)有关的右商McCoy环。

先证明必要性，假设k0(y)≠0并且hk(y)≠0，其中k最小。那么根据公式（*），k0(y)hk(y)∈I[y]。因此存在一个元素r1∈RI使得k0(y)r1=0，意味着F(y)(r1xn-1)=0。若k0(y)=0，那么F(y)xn-1=0。

因此，R[x,α]/(xn)是一个与理想I[x,α]/(xn)有关的右商McCoy环。

再证明充分性，设f(y)=满足f(y)g(y)∈I[y]。由于R[x,α]/(xn) 是一个与理想I[x,α]/(xn) 有关的右商McCoy 环，那么存在一个多项式h( x)=使得f(y)h(x)=0。设ck0∉I，其中k0最小。因此f(y)ck0=0。因此，R是一个与理想I有关的右商McCoy环。

定理1.14设R是一个环且I是R的一个理想，则下面情况等价。

（1）R是一个与理想I有关的右商McCoy环；

（2）R[x]是一个与理想I[x]有关的右商McCoy环；

（3）R[x]/(xn)是一个与理想I[x]/(xn)有关的右商McCoy环；

（4）R[{xα}]是一个与理想I[{xα}]有关的右商McCoy环，其中{xα}是R上任意一组交换不确定数。

证明（1）⇔（2）根据定理1.9可得。

（1）⇔（3）根据命题1.13可得。

（1）⇒（4）设F(y)∈R[{xα}][y]并且G(y)∈R[{xα}][y]I[{xα}][y]满足F(y)G(y)∈I[{xα}][y]。那么F(y)∈R[xα1,xα2,…,xαn][y]，G(y)∈R[xα1,xα2,…,xαn][y]I[xα1,xα2,…,xαn][y] 对 于 一 些 有 限 子 集{xα1,xα2,…,xαn}⊆{xα}。根据（1）⇒（2）并通过归纳，环R[xα1,xα2,…,xαn]是一个与理想I[xα1,xα2,…,xαn]有关的右商McCoy环，所以存在一个元素h∈R[xα1,xα2,…,xαn]I[xα1,xα2,…,xαn]⊂R[{xα}]I[{xα}]使得F(y)h=0。因此，R[{xα}]是一个与理想I[{xα}]有关的右商McCoy环。

（4）⇒（1）与（2）⇒（1）类似。

2 商McCoy环的扩张

设R和S是两个环并且M是一个(R,S)-双模。这意味着(rm)s=r(ms)对任意的r ∈R，m ∈M 和s ∈S。给一个双模M，可以形成

通过使用形式化的矩阵乘法，在T上定义一个乘法

那么T是一个三角矩阵环。

取I=其中I1是R的一个理想并且I2是S的一个理想。那么I是T的一个理想。

命题2.1设T=是一个三角矩阵环，其中R和S是两个环并且M是一个(R,S)-双模。I1是R的一个理想并且I2是S的一个理想，那么T是一个与理想I有关的右（左）商McCoy环当且仅当R和S分别是一个与理想I1和I2有关的右（左）商McCoy环。

证明 先证明必要性，设fR(x)=r0+r1x+…+rmxm∈R[x]，gR(x)r′0+r′1x+…+r′nxn∈R[x]I1[x]满足fR(x)gR(x)∈I1[x]。并且fS(x)=s0+s1x+…+smxm∈S[x]，gS(x)=s′0+s′1x+…+s′nxn∈S[x]I2[x]满足fS(x)gS(x)∈I2[x]。设

并且

那么fR(x)gR(x)∈I1[x]并且fS(x)gS(x)∈I2[x]意味着f(x)g(x)∈I[x]。由于T是一个与理想I有关的右商McCoy 环，那么存在一个元素在TI中使得=0 当i=1,2,…,m时。故ric=sid=0。这表明R和S分别是一个与理想I1和I2有关的右商McCoy环。

再证明充分性，设

并且

是T[x]中两个多项式满足f(x)g(x)∈I[x]。设

并且

那么fR(x)gR(x)∈I1[x]并且fS(x)gS(x)∈I2[x]。

由于R和S分别是一个与理想I1和I2有关的右商McCoy环，那么存在c∈RI1和s∈SI2使得fR(x)c=0并且fS(x)s=0。

因此存在一个元素P=在TI中使得f(x)P=0。

因此，T是一个与理想I有关的右商McCoy环。

给定一个环R和一个双模RMR，R通过M的三角扩张T(R,M)=R⊕M有通常的加法和乘法(r1,m1)(r2,m2)=(r1r2,r1m2+r2m1)。

设T(I,M)=是三角矩阵环的一个理想，其中I是R的一个理想。

推论2.2 设R是一个环并且I是R的一个理想。则R是一个与理想I有关的右商McCoy环当且仅当三角扩张T(R,R)是一个与理想T(I,M)有关的右商McCoy环。