寻根究底 正本清源
——有理数运算再教学*
2023-09-13王远敏刘诗亮四川省成都市蒲江县寿安初级中学611633
王远敏 刘诗亮(四川省成都市蒲江县寿安初级中学 611633)
1 问题呈现,引发思考
有理数运算教学过程中,笔者时常遇到这样的错误:-1+2=-1,-2+(-3)=5,-2×(-3)= -6,2-1×(-3)=1×(-3),….为什么如此简单的有理数运算却频繁出错?笔者认为很简单的有理数运算对这些学生而言并不简单.有理数运算教学俨然成了困扰笔者的噩梦,产生了教学挫败感.
运算能力是初中阶段核心素养的主要表现之一.有理数运算是发展学生运算能力的基础,是后续学习整式运算、方程、不等式、函数等的前提,贯穿于整个初中数学学习的始终,是每个学生必备的基本能力.因此,新课教学后,有必要根据学生出现的问题,认真分析有理数运算为何让这些学生感到焦头烂额、混淆不清,甚至越学越糊涂,揭示问题本质,从根源上解决问题.
2 寻根究底,剖析问题
随着负数的引入,数的运算范围也得到了相应的扩张,小学阶段数的运算则成为有理数运算的一种特例.有理数运算与小学运算的主要区别在于一是负数出现并参与所有运算;二是减法运算中较小数可以减较大数;三是绝对值和新运算(有理数乘方)的加入.对负数及有理数概念和性质的深刻理解是进行有理数运算的基础.学生在小学阶段虽然已经接触过负数,对负数有了初步认识,但并未涉及运算,学生符号意识淡薄,对有理数运算中出现的诸多性质符号和运算符号(部分符号还具有双重身份,既是性质符号又是运算符号)不能依据相关运算法则灵活处理.
有理数运算包括“加、减、乘、除、乘方”5种,实质上由符号运算和数值(绝对值)运算两部分构成.有理数运算种类较多,导致部分学生在法则记忆和应用时产生混淆,尤其是确定计算结果的正负时,出错率较高.比如,学了有理数乘法法则后,学生在做有理数加法时就出现了-2+(-3)=5(同号得正)和-1+2=-1(异号得负)的负迁移情况.又如,当学生忘记用乘法法则如何判定符号时,就出现了-2×(-3)=-6这样用加法法则(同号两数相加,取相同符号)确定符号的做法.而2-1×(-3)=1×(-3)则是运算顺序出了问题.
《义务教育数学课程标准(2022年版)》指出:“运算能力主要是指根据法则和运算律进行正确运算的能力.能够明晰运算的对象和意义,理解算法与算理之间的关系;能够理解运算的问题,选择合理简洁的运算策略解决问题.”[1]综合以上分析可知,导致有理数运算出错的根本原因是学生对运算法则、运算顺序和运算律的理解不深刻、不透彻.法则应用中的错误主要集中在符号运算上;运算顺序出错的主要表现为先算加减后算乘除、先化简双重符号后算乘方等;运算律方面的问题是学生不擅长用运算律简化运算.
3 正本清源,解决问题
运算能力的培养非一朝一夕,是一个不断矫正、不断适应、不断完善、长期坚持的过程.要解决有理数运算中存在的问题,提升运算能力,教师必须重新审视与有理数运算相关的概念和法则,厘清知识的来龙去脉和各知识之间的关联与区别,结合学情,通过有层次、有深度的问题串教学,引发学生新的思考,构建知识体系,弥补新课教学中的缺陷,纠正学生的错误认知.
3.1 理解符号,强化意识
有理数本质上可视为由性质符号和绝对值两部分组成,而小学阶段数的运算不涉及数的性质符号.要让学生接纳有理数、充分理解有理数,必须培养学生的符号意识.数系扩张到有理数后,“+”“-”不仅是运算符号,还是性质符号,具有双重身份.在加减运算中,“+”“-”是运算符号,读作“加”“减”,不能省略;在正负数表示中,“+”“-”是性质符号,读作“正”“负”,“+”通常省略不写.
问题1根据有理数和相反数的知识化简:
(1)+(+5);(2)+(-5);(3)-(+5); (4)-(-5);(5)(-1)-(-2)+(-3)-(+4).
问题2判断下列说法是否正确,并说明理由:(1)带“-”号的数是负数;(2)一个数的相反数一定比它本身小;(3)绝对值越大,这个数越大;(4)一个数的绝对值等于它的相反数,这个数一定是负数.
教学说明 有理数的概念、相反数、绝对值、双重符号化简是有理数运算的知识基础.通过两个问题让学生对相关知识有更清晰、更深入的认识,增强符号意识,培养学生的分类思想、推理能力和应用意识.问题1的第(5)小题化简结果为-1+2-3-4,将“+”“-”视为运算符号时,读作“负一加二减三减四”;视为性质符号时,读作“负一、正二、负三、负四的和”.应让学生通过具体问题充分体会“+”“-”在有理数运算中的双重身份.实际运算中,通常将“+”“-”视为性质符号,运算会更简洁.问题1的解决为学生回答问题2搭建了“脚手架”,两个问题从具体到抽象,逐层递进,促使思维自然生长.
3.2 辨析法则,建构体系
学生的学习是在原有知识和经验基础上自我建构的过程.在学习新知时,如果学生缺乏对知识间整体关联的认识,就会导致知识建构失败或不完整,引起认知混乱.这就需要针对学生的具体问题,让学生经历知识再建构过程.有理数运算法则的新课教学一般按照加、减、乘、除、乘方的顺序进行,知识之间的联系主要体现为顺序性,而缺少跳跃性和整体性,知识碎片化、割裂化、浅表化在所难免.对有理数运算进行综合梳理、深度剖析时,应打破教学先后顺序的禁锢,从整体关联的视角向学生揭示各种运算之间的内在联系,排除法则之间的相互干扰,使知识体系化、结构化、深度化,让学生对有理数运算“见木又见林”.学生在练习、思考、总结的同时,自然而然地经历了有理数运算再建构的整个过程,积累了数学活动经验,改正了错误认知.
问题3观察运算类型并计算:
(1)(-3)+(-4),(-3)×(-4);(2)3+(-4),3×(-4);(3)(-3)+4,(-3)×4;(4)0+(-4),0×(-4).
问题4根据问题3思考有理数加法与乘法法则的区别.
问题5观察运算类型并计算:
(1)(-3)-(-4),(-3)-4;(2)(-3)÷(-4),(-3)÷4;(3)34,(-3)4,-34.
问题6根据以上运算,说一说有理数各种运算法则之间的联系.
教学说明 加法与乘法是有理数运算中最基本的两种运算,也最易引发运算结果符号的混淆.乘法是加法的继承与发展,减法可以转化为加法,除法和乘方可以转化为乘法.问题3和4旨在通过加法与乘法的对比,让学生明晰二者运算结果符号确定方法的差异;通过各类加法(乘法)运算的对比,让学生对加法(乘法)法则有更深刻的理解,从而纠正学生的认知混乱.问题5是减法、除法、乘方运算,多数情况下,这三种运算都是涉及两种运算法则的二次运算,比如减法运算涉及减法和加法法则,运算难度比问题3提升了一个档次.乘方运算中,学生易将 -34当作(-3)4来算,可设计如下问题加以引导:(-3)4与-34哪里不同?(一个有括号,一个没有);括号在乘方运算的什么部分?(底数部分);说明什么?(说明二者底数不同).乘方和乘法混淆时,可让学生将问题5中(-3)4与问题3中(-3)×4的算法进行对比,发现二者的区别.让学生“先观察运算类型再计算”的意图是提醒学生选对运算法则,在计算过程中深入理解各种运算法则之间的区别与联系.问题6旨在让学生通过练习,归纳总结、自我建构,对有理数运算有更深刻的认识,促进知识结构化(图1).实际教学中,还应设计有关分数(小数)的运算,使有理数的类型更全面.特别需要指出的是,用小学阶段运算方法能解决的就按小学方法算,例如15-9,按有理数减法法则转化为15+(-9)反而使运算复杂化.
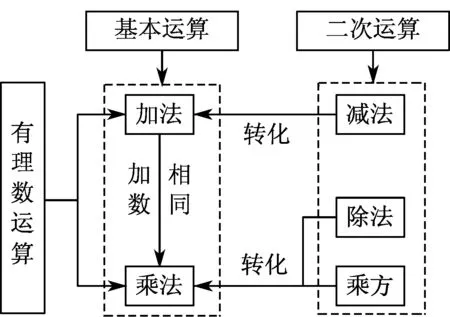
图1
3.3 混合运算,有条不紊
运算顺序也是导致学生有理数运算出错的原因之一.教材中明确地给出了运算顺序的文字描述,规范地呈现了例题解答过程,可学生仍然错误频出,说明学生对运算顺序的理解和重视程度不够,计算时存在随心所欲的现象.为提升学生运算顺序意识,做题前应要求学生总览全题,找出题目中包含的所有运算类型,并在运算过程的每一步用“下划线”或类似记号标记需要计算的部分,外显运算顺序,从直观上提醒学生每一步应该算哪里.
问题7观察运算类型并计算:2+(-2)2×
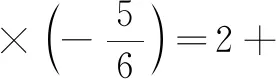
3.4 规范草稿,减少失误
有理数运算中,部分运算过程不要求呈现出来,导致学生容易忽视认真、规范地在题目旁边或草稿本上书写这些运算过程,取而代之的是口算、心算,或者快速且潦草地演算.许多学生所说的“粗心大意”导致计算失误,很大程度上就是因为没有写草稿或写草稿不认真、不规范.比如学生(包括成绩较好的学生)在做含有分数的运算时,用口算或心算就很容易出错.因此,应从初中阶段的起始运算(有理数运算)开始,对学生的草稿提出严格要求,规范学生的草稿书写,特别是易错题计算过程的认真书写,将内隐的运算过程显性化,力求手到、眼到、心到,避免看错、写错、算错,从而有效地减少过失性失误.
3.5 简化运算,提升能力
运算律是通过对一些等式的观察、比较和分析而抽象、概括出来的运算规律,包括加法交换律和结合律、乘法交换律和结合律、乘法对加法的分配律等.运算律的教学,有助于加深学生对运算本质的理解,提升运算能力,感受抽象、推理、转化与化归等基本数学思想.教学中,应让学生理解运算律,经历按运算顺序依次计算和使用运算律简化运算的过程,使学生体会运算律的重要性,养成用运算律简化运算的好习惯.
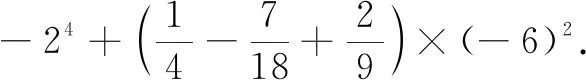
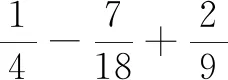
4 三省吾身,教学反思
纪伯伦说:“不要因为走得太远而忘记为何而出发.”教师不但要思考学生“在哪里?”让学生“到哪去?”学生应该“怎么去?”而且要关注每个学生“到了吗?”.日常教学中,总有一些学生因跟不上教师的脚步而掉队,对这些学生而言,学习目标并没有达成.教师应经常“三省吾身”,从学生起点、学习目标、教学方式、目标达成情况等方面来思考我们的教学.
初中学习阶段,每个学生都处于发展过程中,但学生个体间总是存在或多或少的差异,导致发展并不均衡.教学中应充分尊重学生之间的差异,关注每个学生学习目标的达成情况,根据学习中存在的问题,有针对性地设计和实施接下来的教学活动,以学定教,因材施教,不放弃每一个学生,让每个学生都得到应有的发展.
学习过程中,学生难免会出现各式各样的问题,这些问题正是学生对某些知识掌握情况的体现,也是宝贵的教学素材.解决问题的教学不是单纯地告诉学生应该怎么做,而应透过问题发现本质,从根源上加以解决,使学生的认知从“知其然”逐渐向“知其所以然”及“何由以知其所以然”发展.通过对旧知的梳理、辨析、整合、应用,纠正学生的错误认知,让零散、杂乱和琐碎的知识点形成知识链、结成知识网,重新构建相关知识体系,促进知识结构化,使核心素养真正在教学中落地生根.
