一种寻北仪二位置测量法中转位误差影响分析方法
2023-09-13郭锐
郭 锐
(中国船舶集团有限公司第八研究院,南京 211153)
0 引 言
常用的陀螺寻北仪根据惯性原理研制,不易受使用环境的干扰,具有连续工作时间长、精度高等特点,能够为载具提供准确的航向信息[1]。为了消除陀螺常值漂移,工程上常采用旋转定点采样寻北方案,将寻北仪旋转至不同方位停下,根据陀螺在这些方位的静态输出数据进行寻北解算,以此来达到消除陀螺常值漂移的目的,二位置测量方法正是其中最常用的一种[2]。但实际存在的寻北仪陀螺转位误差、载体姿态角误差以及寻北仪安装误差等都会引起陀螺测量采样值出现偏差,影响寻北仪最终输出。为此,本文在文献[3]的基础上采用更为直观的空间解析几何法分析转位误差对寻北仪输出的影响,以代替传统较为繁琐的坐标变换误差分析方法。
1 寻北仪工作原理
寻北仪利用其内部高灵敏度、高精度的陀螺测量地球自转角速度分量,解算出北向与被测方向的夹角。假设北半球上一载体所在地点S纬度为φ,该点地球自转角速度矢量Ω,方向如图1所示。Ω沿水平面的分量为Ωx0,指向北;垂直向上的分量为Ωz0,可以得到
Ωx0=Ωcosφ,Ωz0=Ωsinφ
(1)

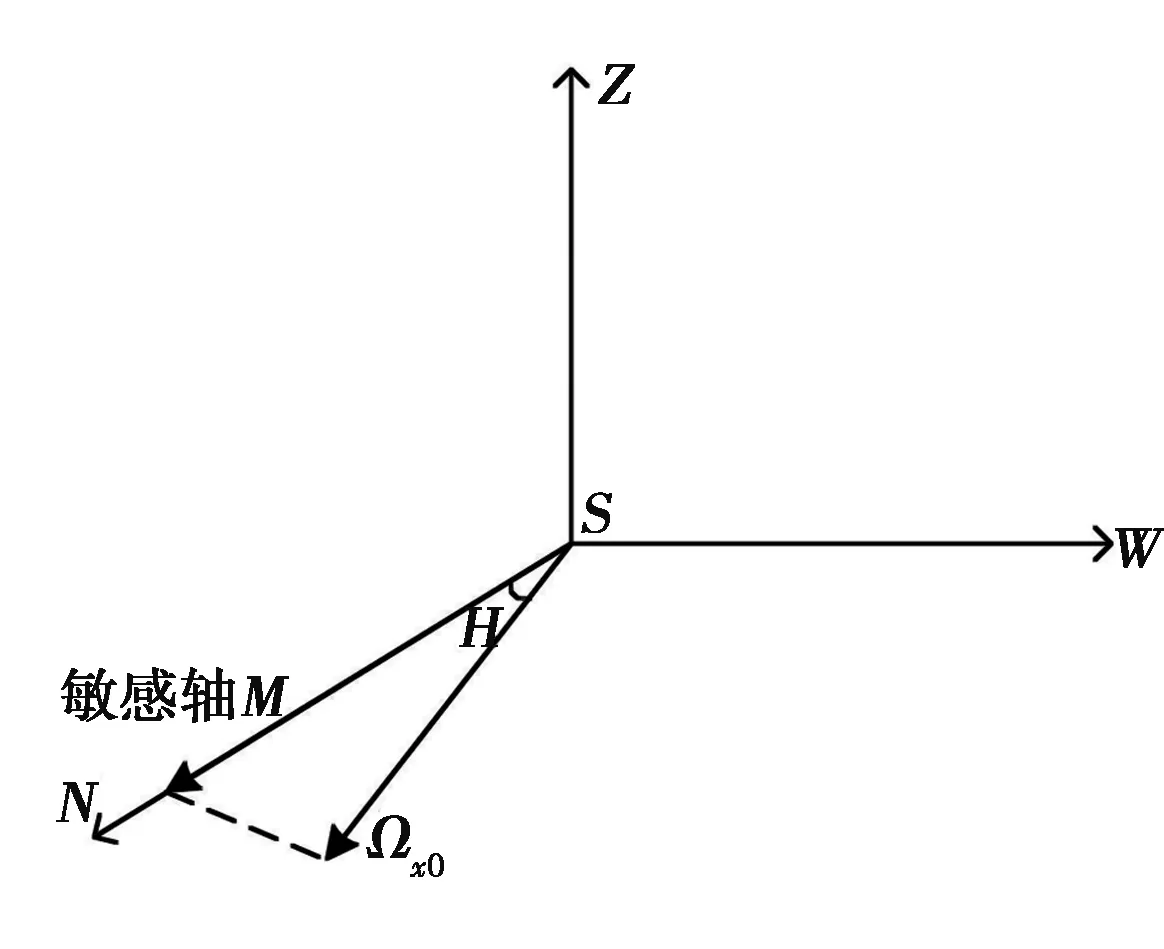
图1 陀螺寻北仪工作原理图
假设寻北仪所在载体完全水平,其与正北的夹角为H,则Ωx0在寻北仪陀螺敏感轴上的分量为
M1=M0+DΩx0cosH=M0+DΩcosφcosH
(2)
式中,M0为陀螺零偏;D为陀螺标度因数。
在Ω、φ确定和零值漂移M0已知的情况下即可求出方位角H(即载体绝对水平、无安装误差的理想情况下寻北仪的输出值):

(3)
2 寻北仪二位置测量法
为了消除M0,根据二位置测量法原理,将寻北仪在式(2)基础上方位角转过180°再采样此时的静态输出。此时陀螺测量值为
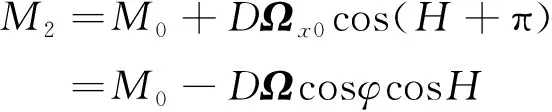
(4)
观察式(2)和(4)不难发现,只要将两式相减即可抵消M0,得到寻北仪输出方位角,即
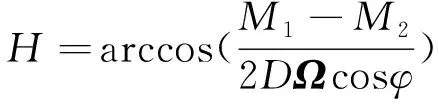
(5)
此时D、Ω、cosφ均为定值,因此寻北仪输出将由这两个位置的陀螺测量值之差ΔM决定。
但实际工程中存在的寻北仪陀螺转位误差、载体姿态角误差以及寻北仪安装误差都会引起陀螺测量值出现偏差,对ΔM造成影响。
3 基于空间解析几何法的转位误差影响分析
3.1 载体空间坐标系的建立
空间解析几何法在具体的坐标系中才能使用,因此在分析转位误差前先建立载体空间坐标系。假设载体质心为O,首先定义地理空间坐标系O-XYZ如图2所示:X轴沿当地子午线,指北为正;Y轴沿当地纬线,指西为正;Z轴垂直于当地水平面,向上为正。显然平面XOY、YOZ、XOZ两两之间相互垂直,3个面将空间分为8个卦限。
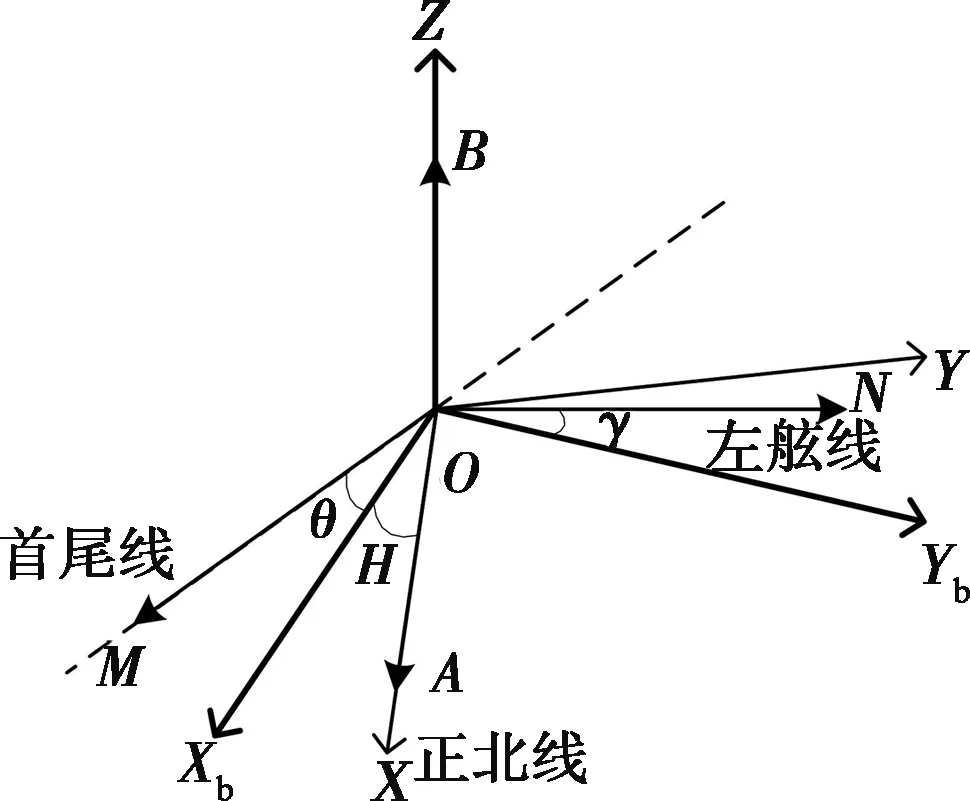
图2 载体空间坐标系
先不考虑安装误差,假定陀螺中心与载体质心、陀螺测量轴与载体首尾线均完全重合,单位向量OM位于陀螺测量轴上,沿载体首尾线向前,另一单位向量ON垂直于OM向左。载体姿态误差角定义如下:纵摇误差角θ为OM与水平面的夹角,即OM与OXb(OM在水平面的投影)的夹角,其测量平面为铅垂面,载体前部抬起为正;横摇误差角γ为ON与OYb(过ON的载体剖面与水平面的交线)的夹角,载体左侧抬起为正。得到正北线OX与OXb的夹角即为方位角H,顺时针为正。
由以上定义可知,OYb位于水平面,OM、OZ位于铅垂面,OXb为水平面与铅垂面的交线,因此可以得到以下垂直关系:OYb⊥OXb、OYb⊥OZ、OXb⊥OZ,即平面XbOYb、XbOZ、YbOZ两两之间互相垂直,这3个平面即可组成载体空间坐标系O-XbYbZ。载体空间坐标系O-XbYbZ可以理解为由地理空间坐标系O-XYZ绕Z轴顺时针转过方位角H形成的。
3.2 转位误差分析
假设载体所在点地球自转角速度水平分量、垂直分量分别为向量OA、OB,则可以得到在载体空间坐标系O-XbYbZ中A点坐标为(Ωx0cosH,Ωx0sinH,0),B点坐标为(0,0,Ωz0)。此时寻北仪处于位置1,M点坐标为(cosθ,0,sinθ),N点坐标为(-sinθsinγ,cosγ,cosθsinγ)。由于M、O、N三点都在载体平面上,载体平面可用MON表示,得到其法线向量为
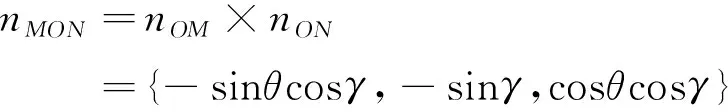
(6)
根据平面的点法表达式,可得到平面MON方程:
xsinθ+ytanγ-zcosθ=0
(7)
寻北仪陀螺测量值即地球自转角速度水平分量OA、OB在敏感轴OM上的投影值之和再加上陀螺零值漂移M0。根据空间直线投影定义可以求得不考虑安装误差时的陀螺实际测量值:
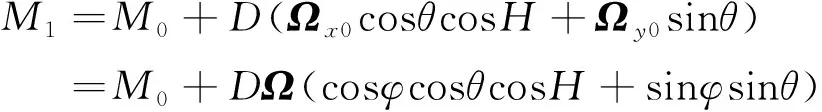
(8)
在实际使用中,由于安装问题,寻北仪陀螺测量轴很难与载体首尾线完全重合,存在误差角[4]。为了便于分析,在不影响推导结果的前提下,假设原点仍在陀螺中心。此时陀螺敏感轴即测量轴向量为OC1,如图3所示,这里将安装误差角放大处理。绕测量轴OC1旋转的误差角对测量值不会有影响,可以忽略,因此定义以下两个误差角表示安装误差:χ为陀螺测量轴OC1绕陀螺纵轴旋转的角度,即OM到OP1(测量轴OC1在载体平面的投影)的角度,顺时针为正,载体面内测量;σ为陀螺测量轴相对于载体平面的俯仰角,即图3中OC1与OP1的夹角,向上抬起为正,其测量平面垂直于载体平面。
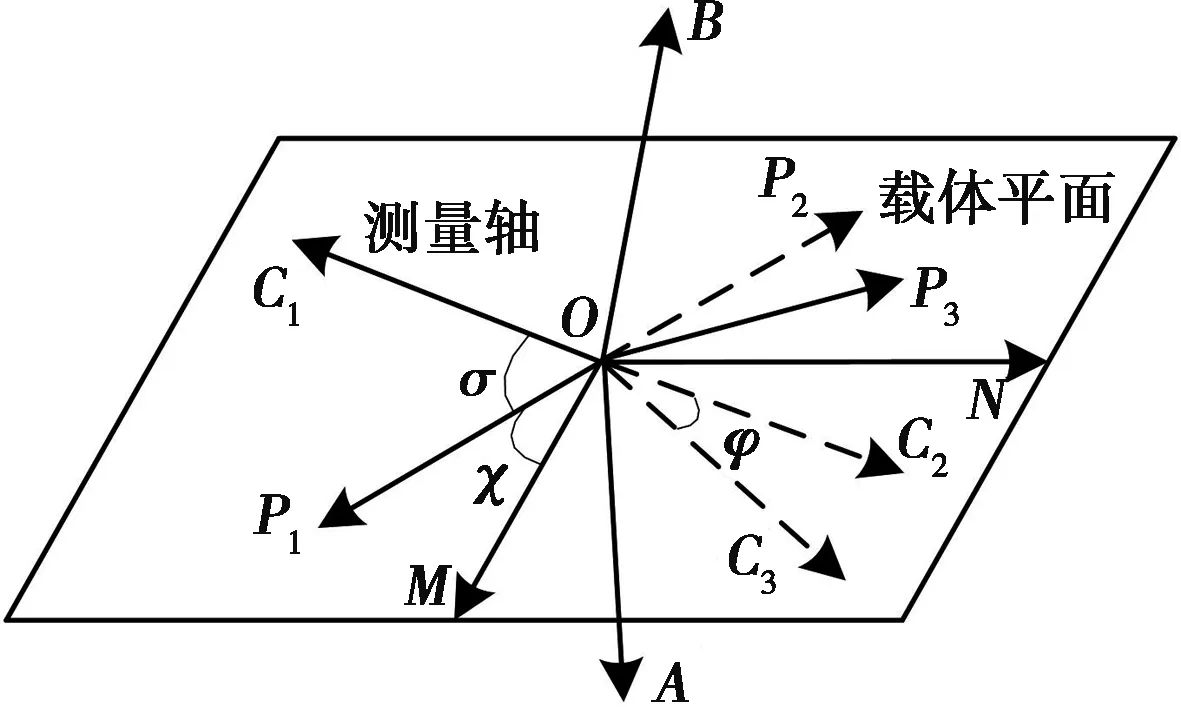
图3 陀螺安装误差角与转位误差角
设单位向量OP1的方向向量为(a1,b1,c1),由于角χ为OM与OP1的夹角,又已知OP1位于载体平面MON,根据空间解析几何相关定义得到OP1方向向量:
a1=cosχcosθ+sinχsinθsinγ
b1=-sinχcosγ
(9)
c1=cosχsinθ-sinχcosθsinγ
设平面C1OP1法线向量为(a2,b2,c2),因为其垂直于平面MON且垂直于OP1,可得
b2=-c1sinθ-a1cosθ=-cosχ
(10)
设测量轴OC1方向向量为(a3,b3,c3),因为其位于平面C1OP1,必垂直于其法线向量(a2,b2,c2),结合角σ的定义和单位向量定义,可求得陀螺测量轴OC1方向向量:
sinθcosγsinσ
(11)
cosθcosγsinσ
此时陀螺测量值为OA、OB在测量轴OC1上的投影值之和再加上M0:
M1=M0+DΩ[cosφ(a3cosH+
b3sinH)+c3sinφ]
(12)
考虑到实际中θ、γ、χ、σ均为小角度,所以其中任意两个角度正弦值的乘积为二阶无穷小量,可忽略,将式(11)代入式(12),得到陀螺位置1测量值:
M1=M0+DΩcosφcosχcosσcosθcosH-
DΩcosφsinχcosγcosσsinH+
DΩsinφ(sinθcosχcosσ+cosθcosγsinσ)
(13)
旋转定点采样只对式(13)中的安装误差角χ、σ产生影响。采用二位置测量法将寻北仪整体顺时针转过180°到位置2,此时测量轴为OC2,当不考虑转位误差时,安装误差角χ2=χ+π,σ2=-σ,陀螺位置2测量值为
M2=M0-DΩcosφcosχcosσcosθcosH+
DΩcosφsinχcosγcosσsinH-
DΩsinφ(sinθcosχcosσ+cosθcosγsinσ)
(14)
转位误差在实际工作中总会出现,假设转位误差角为φ,即图3中OC3与OC2的夹角,由于φ一般很小,因此安装误差角可近似为χ3≈χ+π+φ,σ3≈-σ,则陀螺测量值为
M3=M0-DΩcosφcosσcosθcosHcosχcosφ+
DΩcosφsin(χ+φ)cosγcosσsinH+
DΩsinφ[sinθcosχcosφcosσ-
cosθcosγsinσ]
(15)
由式(13)和式(15)可以得到转位误差φ与陀螺测量值偏差ΔM的关系如下式所示:
cosφ(sinHcosγsinχ-cosHcosθcosχ)cosφ+
sinφsinθcosχ+cosφ(cosHcosθcosχ-
sinHcosγsinχ)]
(16)
3.3 Matlab仿真验证
Matlab版本为R2014a,利用GUIDE编辑的GUI界面如图4(a)所示,验证以下两种情况[5]:
(1)假设载体方位角H=30°,姿态角误差固定为θ=1°、γ=1°,安装误差角固定为χ=1°、σ=1°,根据式(12),不同纬度下陀螺测量值偏差随转位误差角φ(φ∈[-1°,1°])变化的曲线如图4(b)所示。可以看出:纬度越高,转位误差角φ对测量值偏差的影响越大;
(2)当纬度固定φ=30°、姿态角误差和安装误差角均为1°、转位误差角φ=0.5°时,陀螺测量值误差还与方位角H(H∈[-π,π])有关,如图4(c)所示,可以看出:在存在转位误差的情况下,当H=0°时测量值偏差最大。
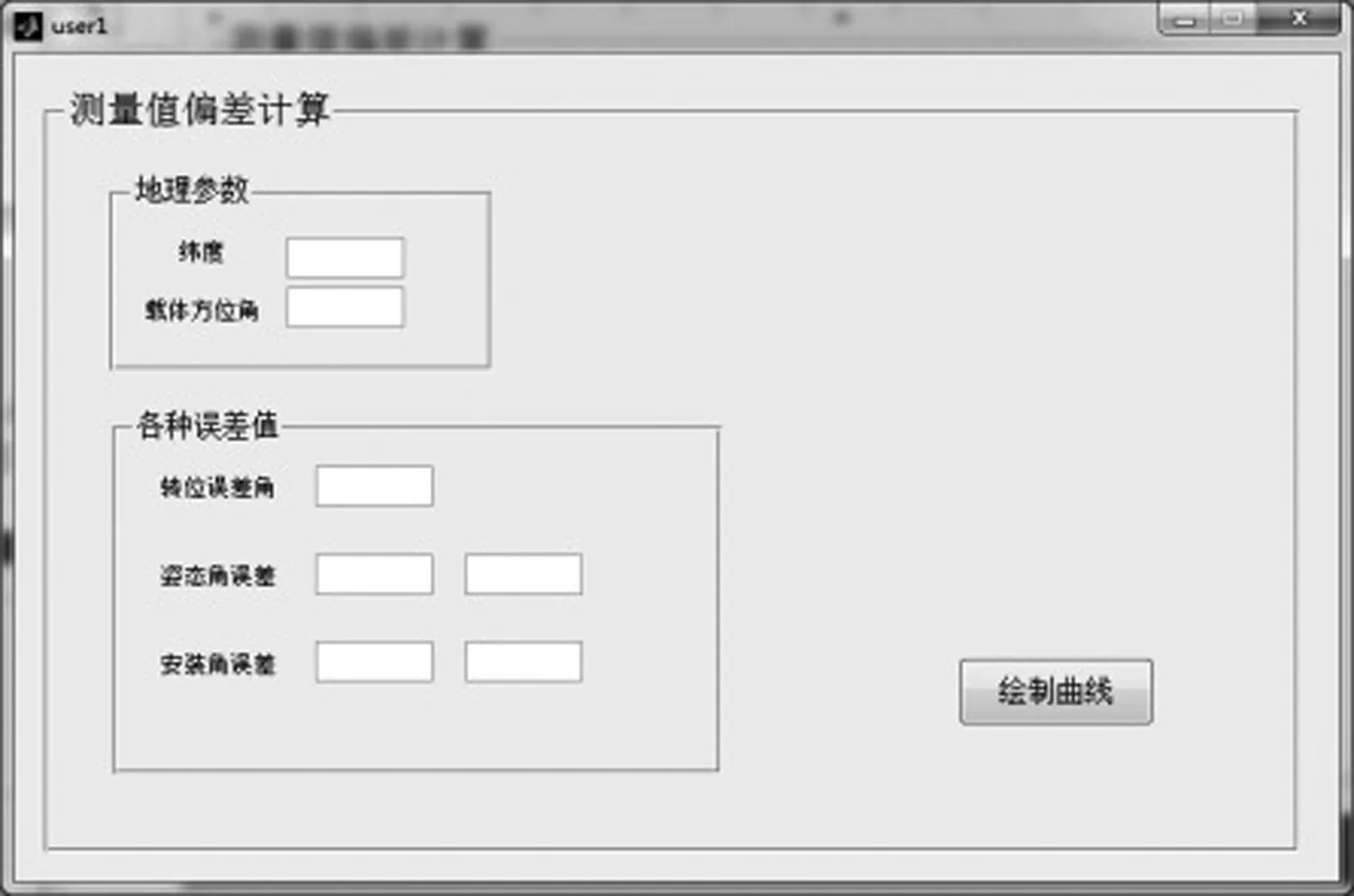
(a)陀螺测量值偏差计算界面

(b)不同纬度测量值偏差与转位误差角关系

(c)测量值偏差与方位角关系
4 结束语
针对寻北仪二位置测量法中转位误差角会影响其最终输出的问题,本文采用空间解析几何法进行分析,较传统方法更为直观。此方法可以扩展用于分析造成陀螺测量误差的其他因素,为寻北仪精度分析提供了一种新的思路,并为误差补偿提供了理论依据。
