基于AHP的显控台结构设计评价方法研究

赵福燕,吴立刚,高 颖

(1. 中国船舶集团有限公司第八研究院,南京 211153;2. 92677部队,辽宁 大连 116000;3. 武汉职业技术学院,武汉 430072)

0 引 言

显控台开发设计方案通常由相关专家,根据自身的经验和主观判断来完成评估,缺少显著的评估依据、准则和科学的分析,容易出现片面或考虑不周全等情况,进而导致误选,造成不必要的损失。

当前,已被证明有效且普遍应用于产品开发的设计理论有层次分析法(Analytic Hierarchy Process,AHP)、Kano模型、发明问题解决理论(TRIZ)、质量功能布置(QFD)等,这些方法各有优势[1],其中AHP可以获得用户对产品的客观评价数据,帮助决策者确定最佳设计方案。本文利用AHP方法对显控台的结构设计进行综合评价,为军用产品领域内研发创新提供一种新思路。

1 AHP简介

AHP是对复杂问题做出决策的一种简明有效的新方法,它把定性分析与定量分析相结合,在一定程度上满足了人们对定量化研究的需要,可分为以下4步[2]：

(1)明确问题,建立层次结构

首先对问题有明确的认识,弄清问题范围、所包含的因素及其相互关系、解决问题的目的等;然后分析系统中各因素之间的关系,建立系统的递阶层次结构:目标层(记为Z)、准则层(记为A)和方案层(记为B)。

(2)构造判断矩阵

对同一层次的各因素关于上一层中某个因素的重要性进行两两比较,构造判断矩阵,如准则层的各因素A1,A2,…,Am对目标层Z的相对重要性,用两两比较法得到判断矩阵A=aijn,其中aij取值如表1所示。

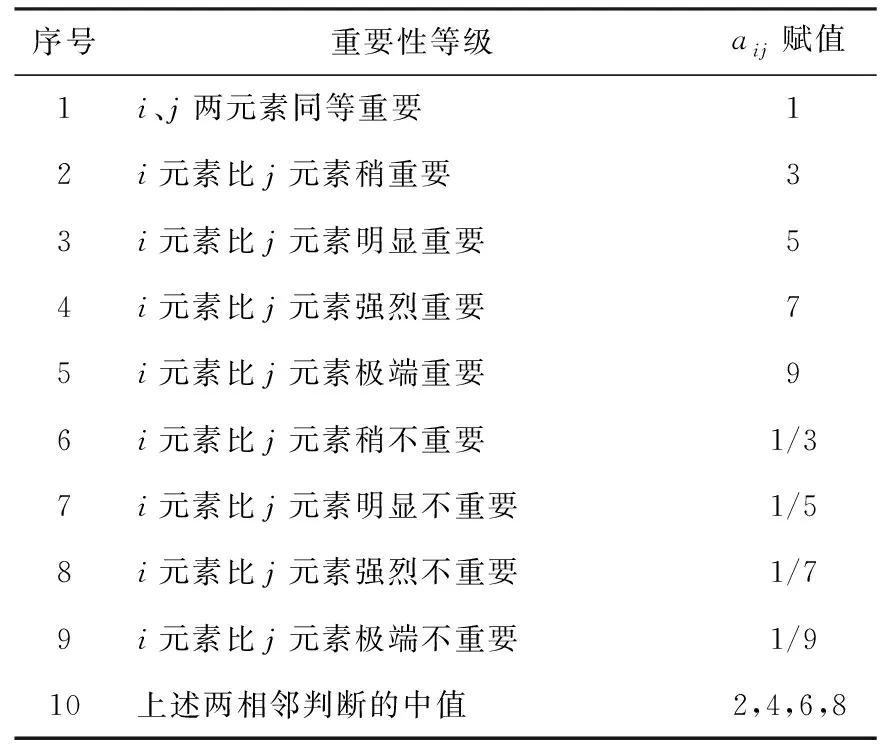
表1 判断矩阵标度定义

aij取1、2、3、9或将它们倒数,因此判断矩阵A又称正互反矩阵,且满足aij=1/aji,j=1,2,3,…,n。

(3)层次单排序及其一致性检验

求出判断矩阵A的最大(绝对值)特征值λmax,再利用特征方程AW=λmaxW解其特征向量W并归一化,即为同一层次的各因素相对于上一层中某一因素的重要性权重,这一过程称为层次单排序。

用列向量平均值法计算权重[3]：

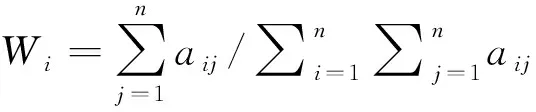
(1)

并求得特征向量W=[W1,W2,…,Wn]T。

计算判断矩阵的最大特征值为

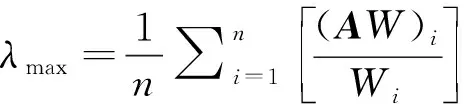
(2)

式中,(AW)i为向量AW的第i个元素。

由于在进行两两比较时带有主观性和片面性,因此有必要进行一致性检验,用来衡量判断矩阵不一致程度的数量指标称为一致性指标,记为CI,定义为

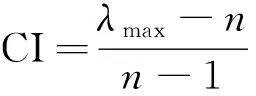
(3)

当CI=0时,判断矩阵是一致的;CI值越大,判断矩阵A不一致性越严重。为确定不一致性在什么范围内AHP可以接受,须引入随机一致性指标RI,如表2所示,其中任意的一阶、二阶判断矩阵都是完全一致的。

表2 随机一致性指标RI

对判断矩阵的一致性检验可以通过计算一致性比例CR来决定,即

CR=CI/RI

(4)

式中,n为矩阵阶数。

当CR<0.10时,认为判断矩阵通过一致性检验[4];否则必须调整判断矩阵,即调整两两比较关系。

(4)层次总排序及其组合一致性检验

逐层计算方案层对于目标层的相对重要性权重,称为层次总排序。设准则层A包含m个因素A1,A2,…,Am,其关于目标层Z的权重为a1,a2,…,am;方案层B包含n个方案B1,B2,…,Bn,其关于准则层中Ai的权重为bi1,bi2,…,bin,那么方案层中B1,B2,…,Bn对目标层Z的权重设为c1,c2,…,cn,其中

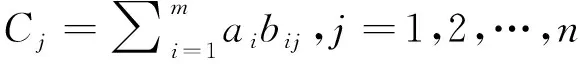
(5)

2 AHP在显控台方案评价中的应用

2.1 建立显控台评价层次

针对显控台结构设计方案优选,寻求最佳解决方案。建立目标层、准则层、方案层如图1所示。专家与用户小组打分确定合理的评价指数,从而明确准则层、方案层各项需求的权重系数,判断矩阵的重要程度等级及其含义。通过层次分析法按权重值大小顺序得出前4个方案如图2所示。

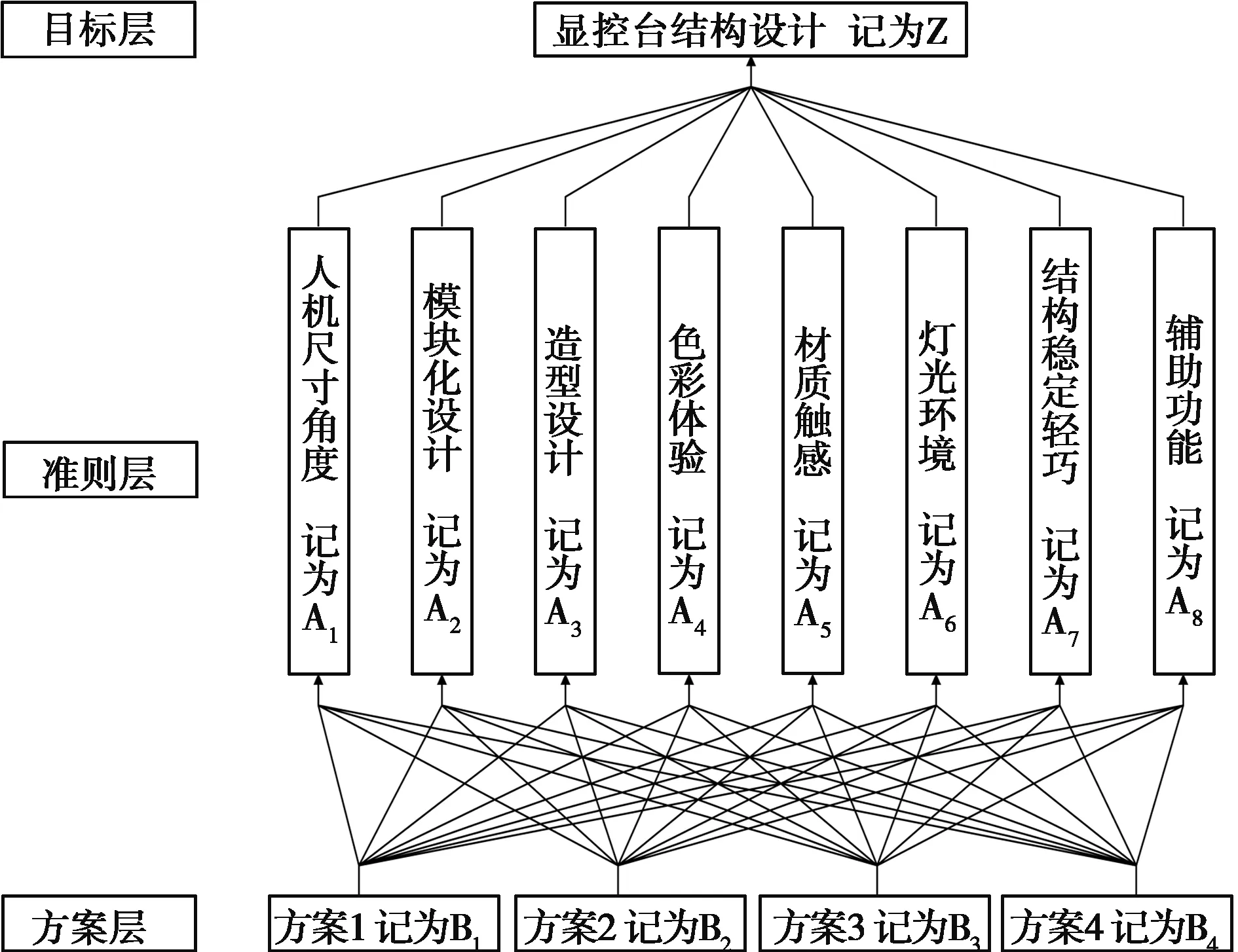
图1 显控台结构设计AHP层次结构图

方案1 方案2 方案3 方案4

2.2 构造显控台判断矩阵

组织显控台研究相关领域不少于6名专家与用户评估打分,将每组准则层数据进行两两比较,构建判断矩阵。首先构造目标层-准则层的判断矩阵A,咨询专家意见,组织专家打分,得到对比数据如表3所示。

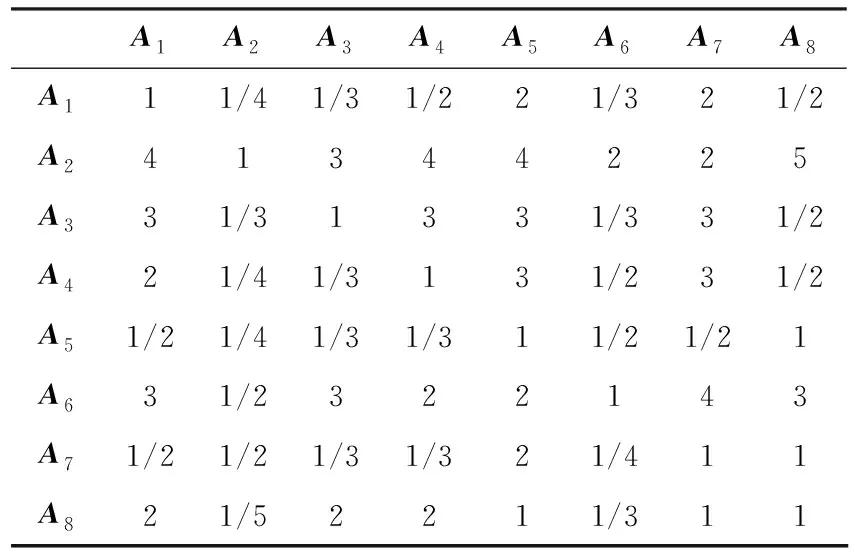
表3 判断矩阵A

2.3 显控台层次单排序及其一致性检验

基于AHP和积法计算判断矩阵的权重值,输入表3数据,得到数值如表4、表5所示。

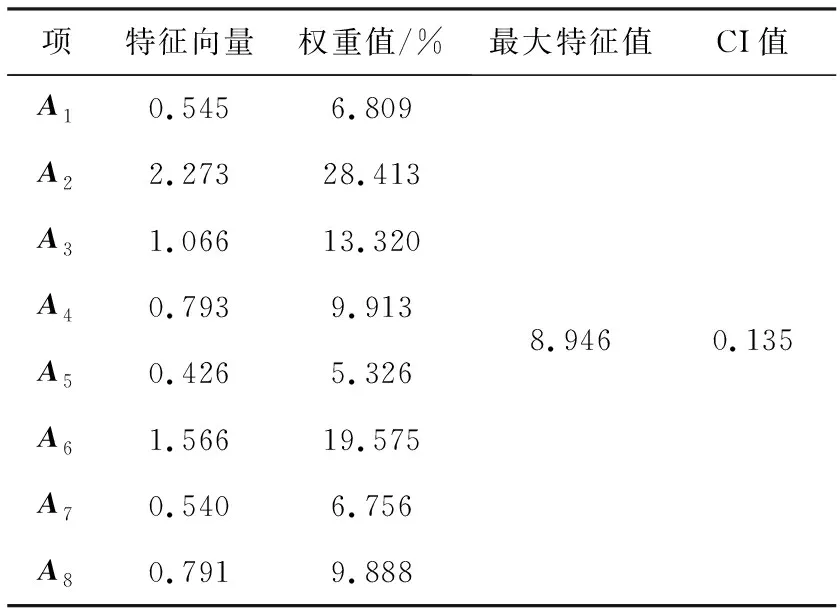
表4 矩阵A的AHP层次分析结果

表5 矩阵A一致性检验结果汇总

得到特征向量W=[0.068,0.284,0.133,0.099,0.053,0.196,0.068,0.099]T,λmax=8.946,CI=0.135。

开展一致性检验,判断一致性矩阵的合理性。当一致性比率CR<0.1时,矩阵才能具有满意的一致性。对于矩阵A：

CR=CI/RI=0.135/1.41=0.096

(6)

因此矩阵具有一致性,判断矩阵满足要求。

2.4 显控台层次总排序及其组合一致性检验

构建准则层-方案层的判断矩阵,对应A1人机尺寸角度、A2模块化设计、A3造型设计、A4色彩体验、A5材质触感、A6灯光环境、A7结构稳定轻巧、A8辅助功能构造的判断矩阵如下,咨询专家意见,组织专家打分,得到对比数据,如表6所示。

表6 判断矩阵A1-A8

基于AHP和积法计算判断矩阵的权重值,以A1-A8矩阵为例,输入表6数据,得到数值分别如表7～22所示。

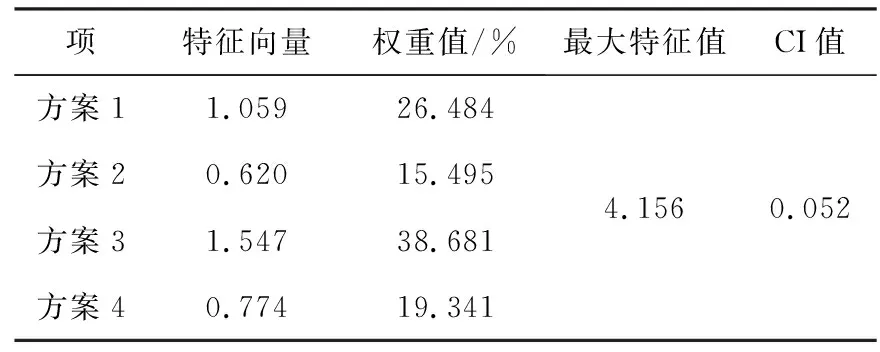
表7 矩阵A1AHP层次分析结果

表8 矩阵A1一致性检验结果

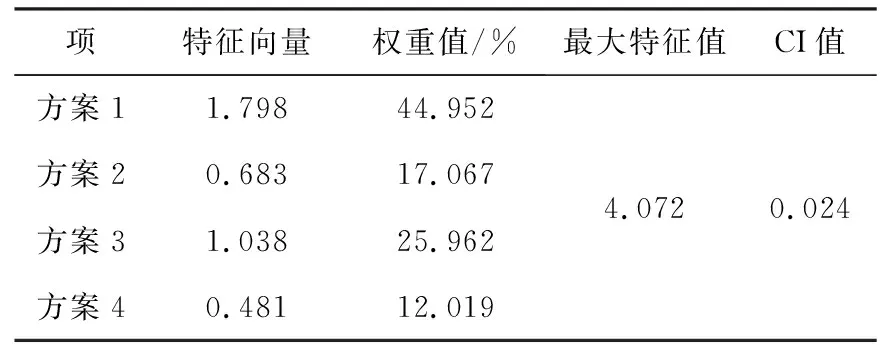
表9 矩阵A2AHP层次分析结果

表10 矩阵A2一致性检验结果

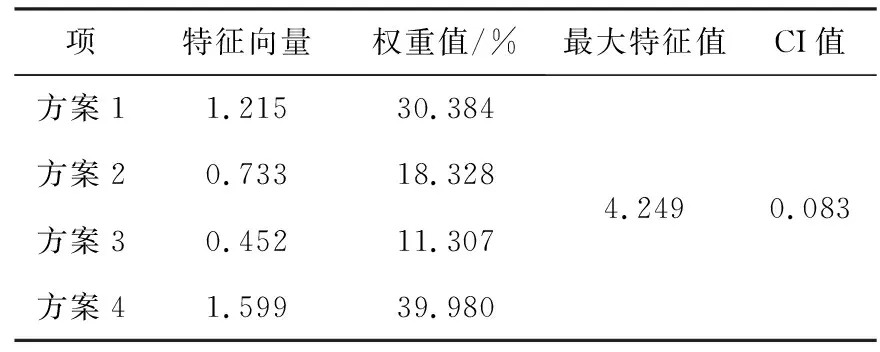
表11 矩阵A3AHP层次分析结果

表12 矩阵A3一致性检验结果

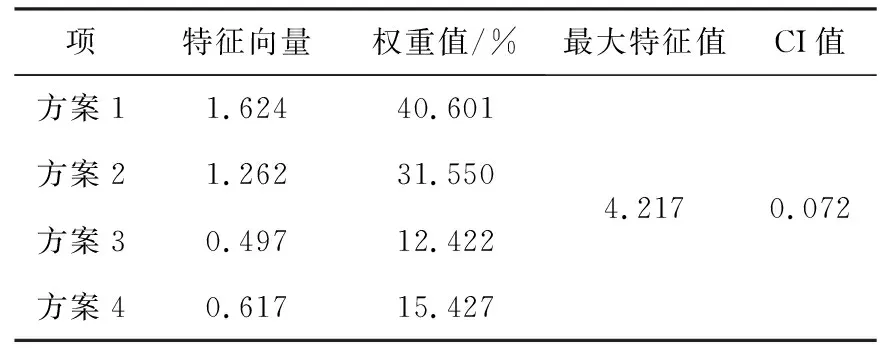
表13 矩阵A4AHP层次分析结果

表14 矩阵A4一致性检验结果

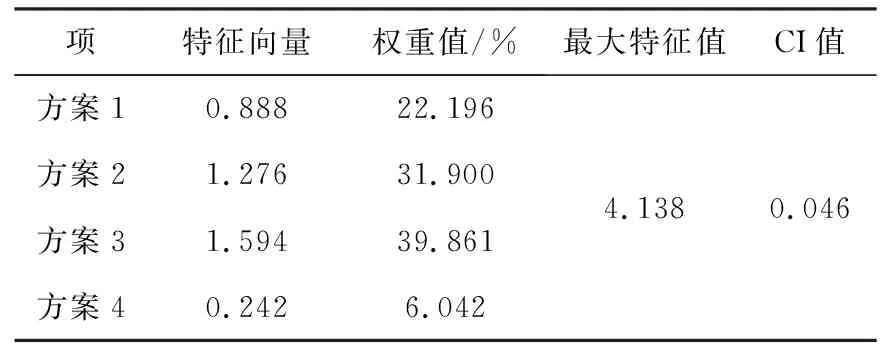
表15 矩阵A5AHP层次分析结果

表16 矩阵A5一致性检验结果

表18 矩阵A6一致性检验结果

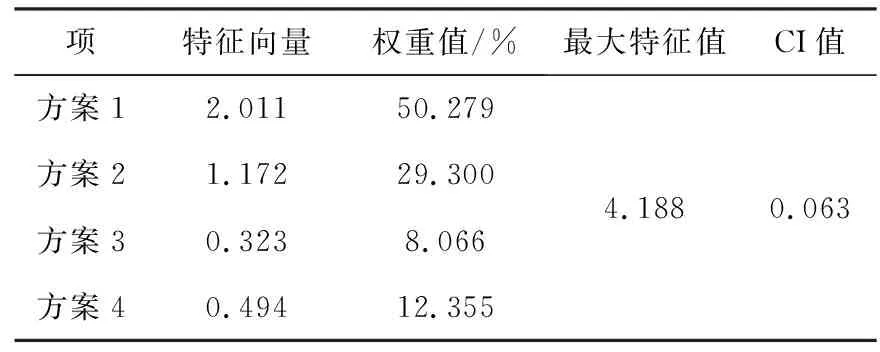
表19 矩阵A7AHP层次分析结果

表20 矩阵A7一致性检验结果

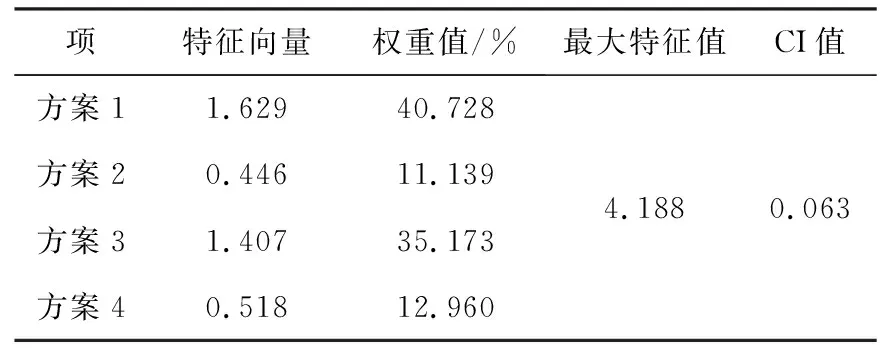
表21 矩阵A8AHP层次分析结果

表22 矩阵A8一致性检验结果

对方案层相较于目标层的权重进行计算排序,即将总目标下需求指标的权重分别与其子需求指标的权重值相乘,得出各方案对目标层的最终权重,如表23所示。可以看出,方案1的权重值最大,更符合设计要求,可以作为最后选择的方案,并在此方案基础上进一步改进,得到最终方案。

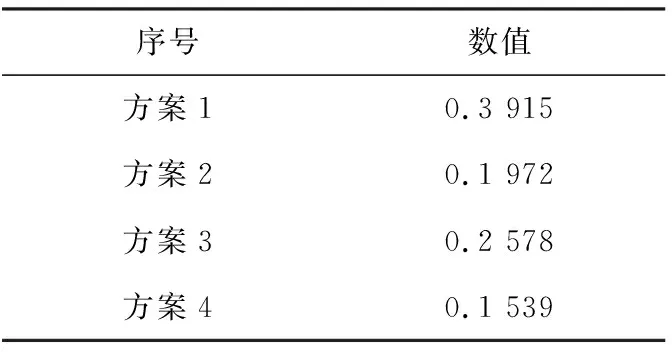
表23 方案层各项权重

3 结束语

本文以专家与用户问卷为基础,结合合理性筛查,建立了较为科学全面的显控台结构设计评价指标体系,提出一种基于AHP的显控台结构设计方案评价优选方法,利用AHP计算各评价指标的权重值,在一定程度上减弱了决策者对结构设计方案评价的主观性与片面性,实现了相对科学的显控台结构设计方案评价。该方法也适用于其他产品设计阶段方案的评价和优选。