4列400 kN气体力迷宫压缩机开式曲轴箱的设计
2023-09-13丛晓梅张建云王云超
丛晓梅,张建云,赵 江,王云超
(沈阳鼓风机集团往复机有限公司,辽宁 沈阳 110869)
1 引言
迷宫压缩机广泛应用于石油化工、炼油、煤制气、天然气等领域各种气体的压缩与输送。当压缩介质不允许与油接触或是含有少许杂质时,普通的活塞环式往复压缩机已不能满足正常工作的需求,为克服活塞环式压缩机的缺点,采用迷宫往复式压缩机。迷宫式活塞为整体式,不与气缸接触,是靠活塞上的迷宫环槽进行密封,完全做到无油润滑,而且速度越快,密封效果越好,大大延长了压缩机使用寿命。随着行业需求越来越大,且受控于国外公司的垄断,迷宫压缩机国产化已迫在眉睫。在国内,迷宫压缩机的开发已渐趋规模,但未形成系列化,机型还有待完善,4列400 kN气体力的大型迷宫压缩机组的研制已被提上日程。
2 迷宫压缩机的结构特点
迷宫压缩机属于立式往复压缩机组,主要由曲轴箱、曲轴、十字头、连杆、气缸、活塞、及填料等部件组成。曲轴箱是支承气缸、曲轴、连杆、十字头及其它所有零部件的本体。承受了机器本身的全部或部分重量,用来连接气缸和安装运动机构,并用作支承座,连接某些辅助部件,如润滑油系统、冷却系统等。承受着压缩机工作时气体压力及转动部件的惯性力,同时还要为传动机构提供定位及导向。曲轴箱分为开式和闭式两种,本文主要介绍开式曲轴箱的结构。开式曲轴箱分为上、下两部分,通过螺柱螺母紧固连接,O形圈密封。
如图1所示,曲轴箱共由4个腔体组成,腔一一般被称为隔离段,一般充保护气,属于气体流动区域,将气体压缩部分和曲轴箱润滑部分隔离开,避免发生接触,产生反应,影响机组正常工作;腔二放置辅助管线,一般导向轴承部件的预润滑管线布置在此腔;腔三为冷却腔,充冷却水,防止十字头在运动过程中过热,烧坏耐磨层;腔四放置曲轴、主轴承及轴承座等关键部件,连接轴头泵和机械密封等辅助机构,从而实现压缩机运转。腔二腔三腔四彼此连通,为传动部件的润滑区域,保证机组安全平稳运行。
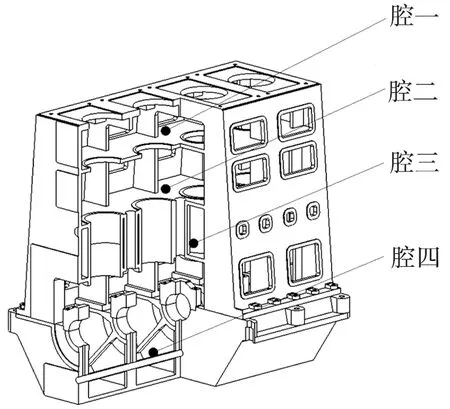
图1 曲轴箱结构图
机组越大重心越高,曲轴箱的承载能力也就越大,对其结构的强度要求更加严格。因此,在其应力集中部位,结构设计强度必须满足要求。
3 曲轴箱的研制
由于迷宫压缩机的活塞不设支承环,迷宫压缩机的气缸都是立式布置,因此,迷宫压缩机的机身也为立式结构,活塞通过机身上的导向轴承进行导向。迷宫压缩机主要通过迷宫结构对气体进行节流降压从而达到密封的效果,而2个相互配合的迷宫密封副间的间隙是影响密封效果的主要因素之一。压缩机中的迷宫密封副有2处:一处是气缸与活塞间的迷宫密封副,一处是活塞杆与填料间的迷宫密封副。为了提高密封副的密封效果,密封副间的间隙就应该尽量小。而要达到减小密封副间隙,机身的设计极为关键。机身滑道与十字头的间隙、活塞杆与导向轴承的间隙都是影响密封副间隙的关键数据。
机身滑道与十字头的间隙需要综合考虑各影响因素而定。首先是要满足十字头的润滑,过小的间隙不利于油膜的行成,从而无法对十字头的运行进行充分的润滑;其次是要有热涨间隙,十字头在运行过程中会产生热量,使十字头体膨胀从而减小与滑道间的间隙,如果间隙留的过小就会使十字头与滑道发生研磨损坏。因此,机身滑道与十字头的间隙值必须是在满足上述条件后的最小值。
3.1 十字头的热膨胀计算
ΔL=L·(T2-T1)·α
(1)
式中 ΔL——热膨胀量,mm
L——十字头直径,mm
T1——十字头制造温度,℃
T2——十字头工作温度,℃
α——十字头材料的线性膨胀系数,×10-6/K
本项目十字头直径为L:435 mm,十字头的制造温度按T1:30 ℃计算,十字头的工作温度按T2:60 ℃计算。十字头材质为ZG230-450,其线性膨胀系数按1.1×10-6/K计算。十字头的热膨胀间隙的计算值为0.144 mm,因此,十字头与机身滑道的间隙最小值不应小于0.144 mm。
上述公式也适用于活塞杆与导向轴承的间隙计算,L为活塞杆直径140 mm,制造温度按T1:30 ℃ 计算,工作温度按T2:60 ℃计算。活塞杆材质的线性膨胀系数按1.1×10-6/K计算。按以上数据计算活塞杆的热膨胀量计算值为0.05 mm。因此,活塞杆与导向轴承的间隙最小值不应小于0.05 mm。
由于迷宫压缩机十字头与滑道的间隙值较小,当压缩机的使用环境温度较低时,压缩机开车初期十字头的温升比滑道的温升要快,这时十字头与滑道极易发生研磨。为了防止这种情况的发生,迷宫压缩机的滑道设计了水腔进行预加热,同时冷却水可将十字头与滑道的摩擦热带走,起到冷却效果,这是迷宫压缩机机身设计的一个特殊之处。滑道水腔的设计如图2所示。
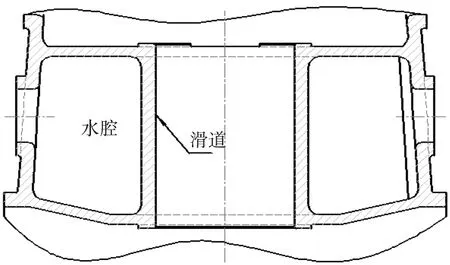
图2 滑道水腔结构
3.2 曲轴箱强度分析
迷宫压缩机对机身的变形要求较为严格,应该尽量减小压缩机在运转过程中由于机身的变形而引起的活塞与气缸之间的同轴偏差。各列气体力通过气缸连接,直接作用在机身上,而综合活塞力通过运动部件作用在机身轴承座上,同时还受十字头部件给的侧向力。为了对机身的整体受力情况和在载荷作用下的变形情况详细分析和掌握,利用分析软件ANSYS对机身结构进行了受力分析。先用Solidworks三维建模,然后对曲轴箱整体进行网格划分。
然后施加载荷,模拟曲轴箱在正常工作中的受力情况,将各个载荷施加到曲轴箱作用面上,如图3所示。当曲柄转角为90°时,所受侧向力最大,为保证结构有足够强度,将一至四列F、G、H、I处均加载最大的侧向力,大小为142 kN;一列承受竖直向上的气体力B,大小为400 kN,第一道轴承承受竖直向下的轴承力为240 kN;二列承受竖直向下的气体力C,大小为400 kN,第二道轴承承受竖直向上的轴承力为120 kN;三列承受竖直向上的气体力D,大小为280 kN,第三道轴承承受竖直向上的轴承力为120 kN;四列承受竖直向下的气体力E,大小为280 kN,第四道轴承承受竖直向上的轴承力为120 kN,第五道轴承承受竖直向下的轴承力为120 kN。

图3 曲轴箱受力示意图
然后进行分析,分析结果如图4~7图所示。

图4 曲轴箱X向形变量

图5 曲轴箱Y向形变量

图6 曲轴箱Z向形变量

图7 曲轴箱应力图
为了减小压缩机在运转过程中由于曲轴箱的变形而引起的活塞与气缸之间的同轴偏差,曲轴箱在最大载荷作用下的变形量应该控制在0.1 mm的范围内。通过分析计算可知机身各向最大变形为0.085 mm<0.1mm,满足设计要求。
曲轴箱材质为HT250,抗拉强度σb=250 MPa,许用抗拉强度σ=25 MPa。通过分析计算可知,曲轴箱整体应力小于25 MPa,最大应力σ=54.16 MPa出现在尖角处,属于局部出现应力集中,但是应力集中面积很小,因此该处计算可认为是合理的,整体满足许用要求。
3.3 开式曲轴箱上下半连接紧固螺栓的强度设计
4列往复式迷宫压缩机,第一、二列与第三、四列工作状态一致,所以在对4列曲轴箱作具体分析时,会简化成2列,方便理解与计算。
受力图及坐标如图8所示。
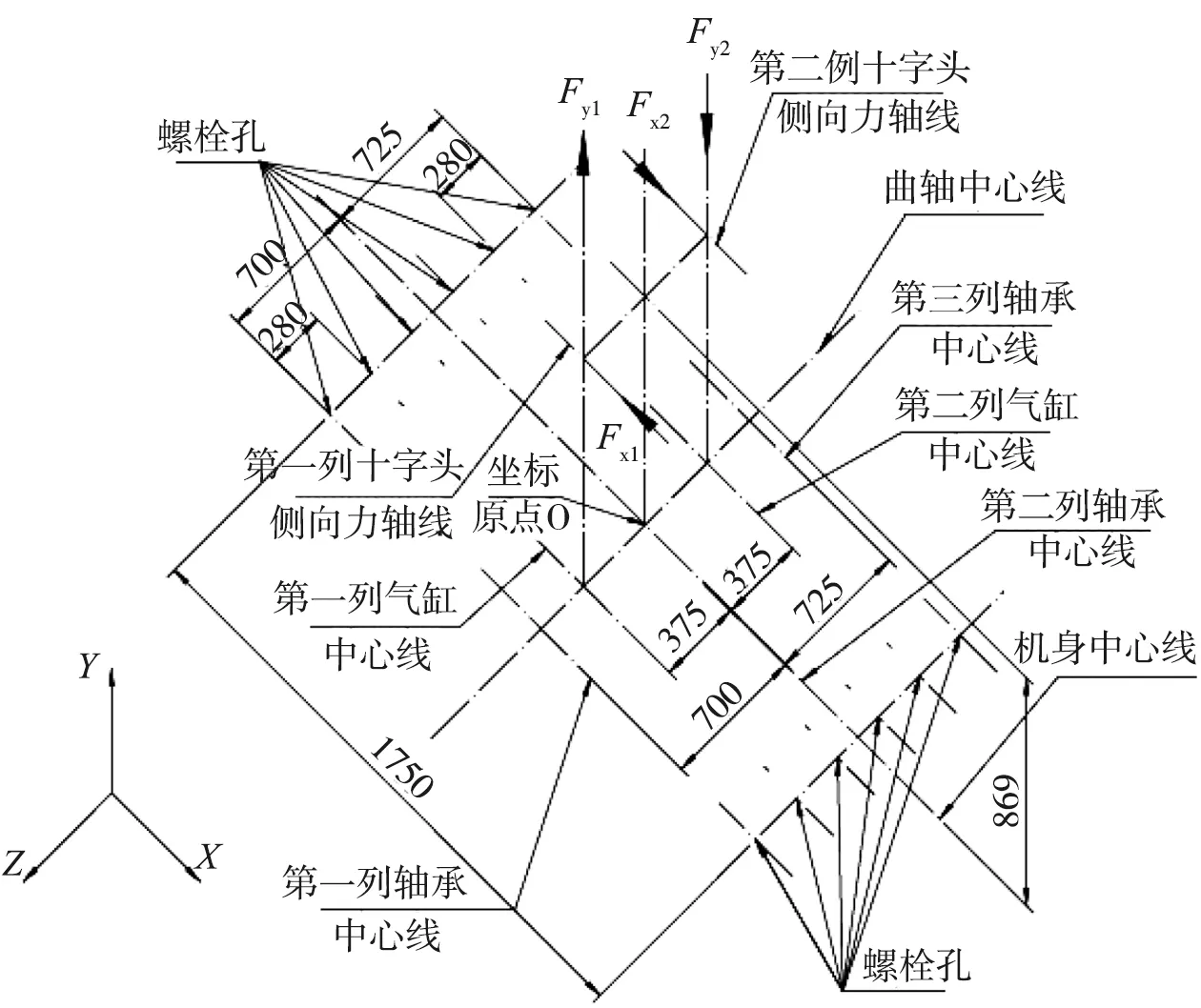
图8 曲轴箱受力分布图
在运行过程中,十字头侧向力发生在曲柄与竖直方向成90°夹角处,已知行程为360 mm,连杆中心距为850 mm,根据勾股定理,即可算出垂直距离869 mm,在此位置处,十字头侧向力最大。
坐标原点O:上、下半曲轴箱对接面的中心
Fx1:第一列十字头侧向力,1.42×105N
Fx2:第二列十字头侧向力,1.42×105N
Fy1:第一列气缸气体力,4×105N
Fy2:第二列气缸气体力,4×105N
Fx=Fx1-Fx2=1.42×105-1.42×105=0
Fy=Fy1-Fy2=4×105-4×105=0.
Fz=0
Mx=Mx1+Mx2
=Fy1·Ly1+Fy2·Ly2
=4×105×0.375 m+4×105×105×0.375
=3×105Nm
My=My1+My2
=Fx1·Lx1+Fx2·Lx2
=1.42×105×0.375 m+1.42×105×0.375
=1.065×105Nm
Mz=0
3.3.1 螺栓组的强度计算
螺栓组所受力矩如图9所示,由图上可见螺栓组受翻转力矩Mx,翻转力矩Mx作用在上、下半曲轴箱对接面内,2列螺栓组内螺栓总数为16个。

图9 曲轴箱受力矩视图
螺栓组所受力矩如图8所示,由图上可见螺栓组受翻转力矩Mx,翻转力矩Mx作用在上、下半曲轴箱对接面内。分析时,假定底板为刚性体,在Mx作用下仍保持平面。同时假定螺栓为弹性体。因承受翻转力矩,原点O右侧各螺栓进一步受拉,第i个螺栓受到工作拉力Fi;原点O左侧各螺栓被放松,不受工作拉力,下半曲轴箱进一步受压阻止曲轴箱翻转。右侧螺栓工作拉力及左侧曲轴箱的支反力对轴线形成的阻抗力矩之和必须与翻转力矩平衡。计算中认为右侧螺栓和左侧曲轴箱各承受一半的翻转力矩,所以右侧螺栓工作形成的阻抗力矩与1/2的Mx平衡,即
(1)
式中Fi——第i个螺栓所受的工作拉力,N
Li——第i个螺栓到翻转轴线的距离,m
M——翻转力矩,Nm
根据螺栓变形协调条件(各螺栓拉伸刚度相同时,其拉伸变形与螺栓中心到翻转轴心线距离成正比)和胡克定律得螺栓的工作拉力与螺栓中心到翻转轴心线的距离成正比,即
(2)
联立(2)、(3)式,解得受力最大的螺栓所受的工作拉力为
(3)
式中Fmax——受力最大的螺栓所受的工作拉力,N
Lmax——受力最大的螺栓到翻转轴线的距离,m
由式(4)可得
3.3.2 螺纹规格的确定
一般联接,工作载荷有变化时
(4)

F——工作拉力,N
F=Fmax
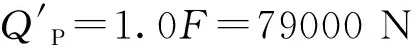
(2)计算螺栓的预紧力QP
(5)
式中QP——预紧力,N

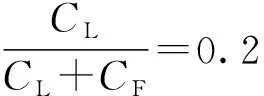
QP=79000+(1-0.2)×79000=142200 N
(3)计算螺栓的总拉力Q
(6)
式中Q——螺栓总拉力,N
Q=142200×1.2=170640 N
(4)初定螺栓直径
(7)
式中 [σ]——许用应力,MPa
σs——屈服点,MPa
S——安全系数
35CrMo调质后的可保证σs≥650 MPa,现取σs=650 MPa
由《机械设计》表6-7a查得,当载荷为变载荷并控制预紧力时,安全系数S=1.2~1.5。现取S=1.5。
(8)
式中d1——螺纹小径,mm

M39×3的普通螺纹d1=33 mm>25.5 mm
现初定螺纹规格为M39×3
3.3.3 螺纹疲劳强度校核
(1)计算应力幅
(9)
式中σa——应力幅,MPa
(2)计算许用应力幅
(10)
式中 [σa]——许用应力幅,MPa
ε——尺寸系数
σ-1t——材料在拉(压)对称循环下的疲劳极限,MPa
Sa——安全系数
kσ——有效应力集中系数
由《机械设计》表6-7a查得,当载荷为变载荷并控制预紧力时,Sa=1.5~2.5,现取Sa=2.5。由《机械设计》表6-7b查得,由σb=800的材料车制的螺纹,kσ=4.8。35CrMo调质后的可保证σb≥860 MPa,取kσ=4.8。由《机械设计》表6-7c查得,公称直径d=39×3的螺栓ε=0.66。
σ-1t=0.23(σb+σs)
(11)
式中σb——抗拉强度,MPa
σ-1t=0.23×(860+650)=347.3 MPa
σa<[σa],螺纹规格为M39×3的普通螺栓满足要求。
4 结语
自1935年瑞士苏尔寿公司开发研制了第一台迷宫压缩机开始,开创了迷宫压缩机应用的先河,并且长期的控制了国内外迷宫压缩机的市场占有率。随着石油化工领域的不断发展,针对不同环境的各种工况,使得迷宫压缩机的应用更加广泛,尤其当压缩介质存在特殊性时,更提高了迷宫压缩机的使用率,市场的需求推动了迷宫压缩机国产化的进程,在国内迷宫压缩机的发展任重道远,我们亦将不断努力,砥砺前行。
