基于时域有限差分算法的光学MATLAB仿真

徐少辉 李波 王连卫

摘   要：以“物理光学”课程为例，基于计算电磁学的有限时域差分法和MATLAB软件图像显示功能，动态地展示光学波动图像，形象化设计课程教学环节。利用MATLAB软件用户操作界面（GUI）功能，让学生自己动手完成结构设计，获得波动光学数据和图像。学生通过观察动态光波传播过程并分析光学图像，提升了对物理光学基础知识的兴趣，有利于深入理解物理机制并提升实践操作能力。

关键词：教学方法；麦克斯韦方程；时域有限差分法（FDTD）；MATLAB

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2023）8-0069-4

高等教育正经历着从应试教育向素质教育、从单一的知识教育向知识能力全面教育的转变。因此，可以通过“学”和“做”相结合的方式讓工科学生掌握坚实的理论基础，并训练其严谨的工匠精神［１－２］。“学”和“做”是学习过程中的一对辩证统一体，古代就有“学而不思则罔，思而不学则殆”的教育，给出的解决方法就是“学而时习之，不亦说乎”，这里的“习”字就包含实践的意思。教师可以在教学工作中给学生创设情境，让其在“做”中探索，在“做”中体验求知的无穷乐趣，以不断获得学习动力和新的发展。因此，以“物理光学”这门课的计算仿真为切入点，通过一系列教学模式和教学方法的改革和创新，来提升和转变工科的基础教学方法，此新教学方式也能够拓展到其他基础学科［３－４］。

光学是物理学专业、电子信息和技术专业开设的必修基础课，要求学生在掌握基本光学理论的基础上，培养他们运用基础知识解决具体光学问题的能力［５－６］。在光学发展过程中，只有很好地掌握物理学基础知识，才能更好地拓展光学专业的应用探索，并理解最新的科研发展，这是一个漫长的学习过程。光学的基础理论可以追溯到１９世纪的麦克斯韦（Ｍａｘｗｅｌｌ）方程组，它是由四个一阶微分方程组成，需要学习大量的物理基础知识和高深的数学才能很好地理解。这些基础知识的限制使得学生很难把握光学知识，感觉其与现代光学技术很遥远。因此，可以利用最新电磁学发展成果反哺教学，利用编制好的计算机程序展示“物理光学”中的具体物理图像。借助这些图像，让学生尝试自己解决一些光学问题，使其逐渐走向最新光学科技前沿。国外的课程中也有类似的构思，如美国麻省理工学院（ＭＩＴ）的电磁学公开课中就有利用电磁计算直观地展示波的传输特性的案例。澳大利亚悉尼大学的Ｉａｎ Ｃｏｏｐｅｒ教授完成了一系列的电磁计算案例，直观地展示了光波的传输特性，并应用于光学课程教学。而国内的四川大学、华侨大学［７］、国防科技大学［８］等高校也都尝试基于计算电磁学去提升光学课程教育。因此，把计算电磁学的最新科研进展应用于教学，精心设计光学物理图像的动态展示，可以激发学生不断探索的欲望。另外，让学生在创设的物理情境中主动学习，能不断获得新的学习动力，并提升创新能力。

1    计算方法简介

随着计算机性能的提升，计算电磁学得到了快速发展。从１９６６ 年Ｙｅｅ在解决电磁散射问题中提出最初思想到现在，时域有限差分算法（Ｆｉｎｉｔｅ Ｄｉｆｆｅｒｅｎｃｅ Ｔｉｍｅ Ｄｏｍａｉｎ，简称ＦＤＴＤ）已经历了五十多年的发展［９－１０］。ＦＤＴＤ能够计算Ｍａｘｗｅｌｌ电磁波方程，得到各种结构的电磁波传输特性，并可以模拟出各个时刻的电磁场分布。另外，ＦＤＴＤ的方便性和准确性也得到了理论和实验上的检验。实现ＦＤＴＤ计算方法的三大关键要素分别为差分格式（包括解的稳定性）、激励源和吸收边界条件。

1．１    差分格式

基于Ｙｅｅ 元胞图，每一个磁场分量有四个电场分量环绕。同样，每一个电场分量也由四个磁场分量环绕。这种电磁场分量的空间取样方式符合法拉第定律和安培环路定律的自然结构，电磁场各分量的空间相对位置也适合于Ｍａｘｗｅｌｌ的差分计算，能够恰当地描述电磁场的传播特性。因此，给定相应电磁问题的初始值及边界条件后，利用 ＦＤＴＤ 方法就可以逐步求得各个时刻的空间电磁场分布。

1．２    激励源

1．３    吸收边界条件

ＦＤＴＤ计算过程中，往往只能选择有限的空间范围，只对计算区域内部的网格上的电磁场数值有效。电磁波到达边界时，理论上应该继续向外界传播。实际上，电磁波将在边界上发生强烈反射，反射回来的电磁波与计算区域中的电磁波发生重叠，导致假的计算图像和错误的计算信息。因此，需要引入吸收边界条件，使得计算区域的边界上，电磁波如同在自由空间一样无反射地传播。人们已经发展出了各种吸收边界条件，如Ｍｕｒ、Ｌｉａｏ和人为构造的ＰＭＬ（Ｐｅｒｆｅｃｔｌｙ Ｍａｔｃｈｅｄ Ｌａｙｅｒｓ）等。

利用ＭＡＴＬＡＢ软件的用户交互式（ＧＵＩ）功能，学生自己动手修改参数，并基于ＦＤＴＤ获得光波传输图像，让学生在“做”中探索，在“做”中体验求知的乐趣。

2    教学思路和过程

由于“物理光学”课程主要针对大学二年级学生，他们的数学计算能力、计算机编程能力和工程训练都较弱。基于此，分两步完成教学任务。

第一步，通过编制好的计算电磁学程序，利用ＦＤＴＤ求解Ｍａｘｗｅｌｌ方程，得到光波传输数据和动态图像（可以录制为电影模式）。让学生通过观察动态图像的方式理解光学物理现象，也能给学生展示光学科研领域的最新进展，让其打开眼界和思路。

第二步，学生利用ＧＵＩ功能操作计算程序、设计实验结构、改变计算仿真参数。通过观察光学图片和动画，讨论各个参数对物理性质的影响，从而培养学生的动手能力和创新能力。

2．１    光学物理图像的展示部分

做一个表格，把“物理光学”课程中主要物理问题列出。基于ＦＤＴＤ方法做出一系列展示程序，并整理成一个应用程序集，用于演示平面波、球面波（柱面波）、介质界面的反射和折射、光波的全反射、光的干涉、光的衍射和光栅衍射等。在教学过程中，利用ＭＡＴＬＡＢ平台运行ＦＤＴＤ程序，让学生直观地感受电磁波的演变过程和物理图像。

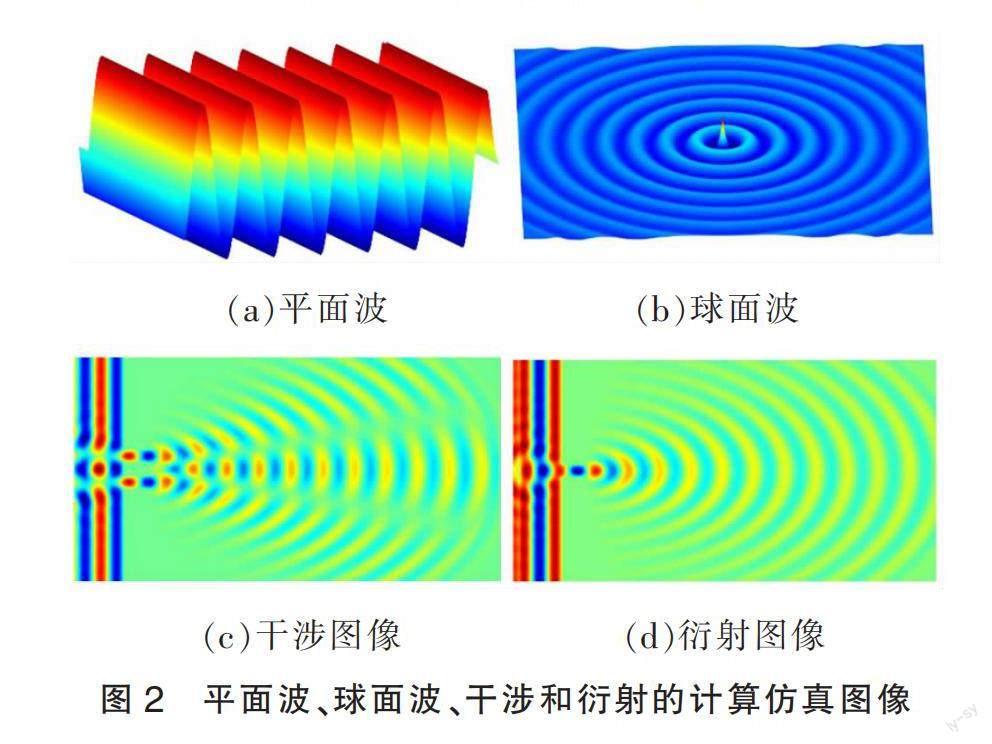
显示界面（图１）列出了不同的物理过程，选择感兴趣的物理过程，点击Ｓｔａｒｔ 按钮，就可以观察到物理图像随时间的动态演变过程。图２是实例中展示的光学图像，分别是平面波的传输、球面波的传输、双缝干涉和单缝衍射过程。学生观察电磁波的演变过程后，可以很好地理解电磁波的传输特性。这是一个开放式展示程序，能逐步把新开发出来的应用程序加入其中，使教学内容更加丰富。

2．２    实践操作部分

二年级学生不易掌握模拟计算的源程序和相关算法，让他们修改源程序来实现不同的物理过程还很困难。因此，使用更友好的ＧＵＩ来实现物理过程的设计以及物理图像的模拟计算，会更加容易。让学生观察计算得到的图片和动画，讨论各个参数对光学性质的影响，可以深入地理解物理机理，也可以锻炼他们的数据分析能力和创新能力。

2．２．１    反射和折射的仿真实验

不同介质界面处光的反射和折射过程是常见的自然现象，虽然中学时就学了反射和折射定律，但直到“物理光学”课上，才获得了反射率和折射率的定量关系（菲涅耳公式）。因此，基于时域有限差分法，利用ＧＵＩ功能开发了介质界面反射和折射的仿真程序（图３），以波动方式理解光的反射和折射现象。具体操作包括：

（１）结构设计界面：选择或修改参数，包括入射波长（５ μm～２０ μm）、入射介质和出射介质的折射率、入射角度（０°～９０°）以及计算时间等。然后，点击操作按钮可获得不同的物理图像。

（２）选择Ｒｕｎ按钮，可以获得由菲涅耳公式计算得到的介质界面的反射率和透射率结果，并标记布儒斯特角（对于Ｐ光，或者ＴＭ模式）和全反射临界角，如图３（ａ）所示。

（３）输入入射波长（５ μm～２０ μm），入射角度（０°～９０°）和计算时间，选择Ｓｈｏｗ按钮，基于ＦＤＴＤ方法求解Ｍａｘｗｅｌｌ方程，确定不同入射角度时反射和折射的波动图像。

在玻璃（折射率１．５）／空气（折射率１．０）界面处，计算得到的反射率和透射率结果如图３（ａ）所示。同时，也可以得到布儒斯特角（对于Ｐ光，或者ＴＭ模式）为３３．８０°，全反射临界角为４１．８１°。小角度（入射角２５°）入射情况，如图３（ｂ）所示，光波以折射现象为主，大部分电磁波通过界面进入空气中，显示出较大的折射角。也可以从波动图形中观察到弱的反射率（约５％），其主要表现为光强度的明暗变化，对应光波的干涉图样。这是由于入射波和反射波满足干涉条件，在此区域相遇时发生干涉现象。对于大角度（入射角５５°）入射情况，如图３（ｃ）所示，光波以反射现象为主，大部分电磁波被反射进玻璃中。由于入射光线和反射光线的偏移，导致全反射过程中的古斯－哈恩斯（Ｇｏｏｓ－Ｈａｎｃｈｅｎ）位移现象［５－６］。反射光与入射光的叠加区域也出现了明显的干涉现象。同时，要注意到折射光并没有完全消除，透射进入空气中的光波强度以指数衰减，这就是全反射现象中的隐失波特性。学生通过自己动手实践操作，可以深入理解介质界面的反射和折射现象。

2．２．２    光学干涉和衍射仿真实验

光波的干涉和衍射现象是“物理光学”的重要内容，因此，基于时域有限差分法并利用ＧＵＩ设计了干涉和衍射现象的操作界面（图４），以波动方式形象化地展示光的干涉和衍射现象。具体操作如下：

（１）结构设计界面。输入参数（狭缝数，狭缝大小，狭缝间距）后，右端显示结构图形（按Ｓｈｏｗｐｉｃｔｕｒｅ键）。

（２）确定光波的波长并运行程序。输入光波的波长，选择平面（２Ｄ）或者立体（３Ｄ）显示，运行计算程序（按Ｒｕｎ键）。

（３）观察计算结果。观察计算得到的动态干涉（或者衍射）图形（图５），以及不同位置光波干涉强度分布图（图６）。

以计算结果为例，在空气（折射率１．０）中设置狭缝宽度为４ μm、间距为１０ μm，按Ｓｈｏｗｐｉｃｔｕｒｅ键可得到图４所示的杨氏双缝结构图。当光波波长为５ μm时，按Ｒｕｎ键可得到双缝干涉图形，如图５所示。可以观察到明显的光波强弱变化，三个干涉峰向外传播。用三维图像显示是为了方便观察光强的变化。考虑到ＦＤＴＤ计算范围有限，在光学近场范围内（菲涅耳衍射），随着通过狭缝的两束光波向外传播，干涉峰强度发生明显变化。首先，显示为两个明显的峰，即两个光源还处于相互独立的状态，如图６（ａ）所示。随着传播距离的增加，两个光源的光波发生重叠，得到中间强度最大的光波分布图，如图６（ｂ）（ｃ）所示。随着传播距离的增加，中间区域出现三个峰，如图６（ｄ）所示。

可以对此干涉和衍射仿真程序进行拓展研究。例如，研究单缝衍射现象和光栅衍射现象（３到７个狭缝）。对于双狭缝结构，还可以改变狭缝大小、狭缝间距和入射波波长等参数，定量研究这些参数对干涉图形的影响。干涉和衍射图形的展示和数据分析过程，非常考验学生的光学基础知识，有助于他们对“物理光学”课程基础知识的理解。另外，此仿真实验程序非常适合作为开放性仿真实验，学生可以基于此程序自主设计新结构，独立操作创新型仿真实验，获得不同结构下的干涉和衍射图像。

3    结  论

针对求解Ｍａｘｗｅｌｌ电磁波方程的难点，通过ＭＡＴＬＡＢ平台运行求解Ｍａｘｗｅｌｌ方程的ＦＤＴＤ程序，计算不同环境下的电磁学问题。模拟完成“物理光学”中的光学部分，形象地展示了电磁波图像和最新的光学科研进展，让学生直观感受光学的演变过程和物理图像，提升其学习兴趣。利用ＧＵＩ功能建立电磁学实验仿真平台，在教学过程中进行多参数光学仿真实验，为设计型和研究型仿真实验创造条件。也能把动态光学演变过程展示给学生，培养其创新能力。此思路虽然是在高校教学中发展而来，但可以很方便地拓展到中学物理教学中。

参考文献：

［１］史峰． 高等教育中现代教育技术的应用研究［Ｊ］． 课程教育研究，２０１７（２７）：６１－６２．

［２］顾培蒂． 可视化技术在教育中的应用［Ｄ］． 北京：北京师范大学，２００８．

［３］徐宁． “物理光學”研究型教学模式探索与实践［Ｊ］.电气电子教学学报，２０１２，３４（３）：１０３－１０５．

［４］黄元申，李柏承，徐邦联，等． 物理光学本科教学体会［Ｊ］.上海理工大学学报（社会科学版），２０１４，３６（３）：２９３－２９６．

［５］梁铨廷． 物理光学（第５版）［Ｍ］.北京：电子工业出版社，２０１８．

［６］钟锡华． 现代光学基础（第２版）［Ｍ］.北京：北京大学出版社，２０１２．

［７］周权． ＦＤＴＤ方法在波动光学教学中的应用探索［Ｊ］.物理通报，２０１９（４）：１２－１６．

［８］林志立，陈子阳，陈旭东，等． 基于ＦＤＴＤ和ＭＡＴＬＡＢ的光学理论课程可视化辅助教学研究［Ｊ］． 教育现代化，２０１９，６（８２）：１７３－１７５．

［９］Ｙｅｅ Ｋ Ｓ． Ｎｕｍｅｒｉｃａｌ ｓｏｌｕｔｉｏｎ ｏｆ ｉｎｉｔｉａｌ ｂｏｕｎｄａｒｙ ｖａｌｕｅ ｐｒｏｂｌｅｍｓ ｉｎｖｏｌｖｉｎｇ Ｍａｘｗｅｌｌｓ ｅｑｕａｔｉｏｎｓ ｉｎ ｉｓｏｔｒｏｐｉｃ ｍｅｄｉａ［Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ａｎｔｅｎｎａｓ Ｐｒｏｐａｇａｔｉｏｎ ，１９６６，１４（３）： ３０２－３０７．

［１０］Ｔａｆｌｏｖｅ Ａ，Ｈａｇｎｅｓｓ Ｓ． Ｃｏｍｐｕｔａｔｉｏｎａｌ Ｅｌｅｃｔｒｏｄｙｎａｍｉｃｓ：Ｔｈｅ Ｆｉｎｉｔｅ－Ｄｉｆｆｅｒｅｎｃｅ Ｔｉｍｅ Ｄｏｍａｉｎ Ｍｅｔｈｏｄ，３ｅｄ ［Ｍ］.Norwood，MA： Ａｒｔｅｃｈ Ｈｏｕｓｅ，２００５．

（栏目编辑    贾伟尧）