基于溶蚀速率的灰岩边坡服役寿命研究

李 泽, 杨元浩, 刘文连, 许汉华, 张小艳

(1.昆明理工大学 建筑工程学院, 云南 昆明 650500; 2.中国有色金属工业昆明勘察设计研究院有限公司,云南 昆明 650051; 3.昆明理工大学 电力工程学院, 云南 昆明 650500)

1 研究背景

近年来,灰岩边坡稳定性问题受到广泛关注,灰岩边坡的稳定性主要受岩体性质、结构面和节理等因素的影响。工程岩体一般为不连续结构面和岩石共同构建的非贯通节理岩体,岩体结构面的分布和力学特性对岩体整体的力学特性起着决定性作用,失稳过程通常为结构面的扩展和贯通[1-3];此外,岩溶也是诱发边坡变形及失稳破坏的一个重要因素,岩溶化边坡在工程中除了具有一般坡体的工程特点外,还会受到溶蚀作用的影响,增大了此类边坡发生变形失稳的概率[4-6]。灰岩溶蚀作用受岩性条件及溶蚀环境的控制[7-8],多沿岩体中的裂隙发生,且大多为高角度裂隙,裂隙溶蚀扩展受雨水的侵蚀性影响[9-11]。在灰岩边坡的服役过程中,由于灰岩岩体受溶蚀而使得结构面的长度和贯通率增大,导致岩体抗剪强度减小[12-13],灰岩边坡的长期安全性会逐渐降低,致使工程中灰岩边坡在服役一定年限后时常发生失稳破坏,给人民生命财产带来重大损失。

在边坡服役寿命的研究中,陈洪凯等[14]运用断裂力学方法,建立了处于临界状态的主控结构面在暴雨状态条件下的疲劳断裂寿命计算方法,但需要通过年降雨量来换算出服役寿命;简文彬等[15]基于材料的疲劳试验与边坡结构应力分析,采用S-N曲线与Miner疲劳累积损伤理论体系进行了边坡疲劳寿命的分析与估计。目前工程界还没有完善的基于溶蚀速率的灰岩边坡服役寿命的计算方法。

鉴于此,本文以灰岩边坡为研究对象,基于边坡溶蚀衰减速率,建立灰岩边坡的长期服役的稳定性非线性数学规划模型,使用“序列二次规划法”求解数学规划模型,获得灰岩边坡的服役寿命,为灰岩边坡的设计提供理论指导。

2 灰岩边坡溶蚀

灰岩是石灰岩的简称,是以方解石为主要成分的碳酸盐岩,主要化学成分为CaCO3,非常易溶蚀。很多岩质边坡由于受工程开挖的影响,坡体内部原有的应力平衡条件被破坏,坡体为了适应新的受力条件,自身发生结构上的调整,形成卸荷裂隙,为外界溶蚀影响因子提供了进入的通道[16],导致灰岩边坡中的结构面在降水以及大气中CO2的作用下发生溶蚀[17-18]。随着时间的推移,结构面的长度会增加,结构面的抗剪参数也会随着溶蚀而发生衰减[19-20],灰岩边坡的长期安全性降低。

若要准确预测灰岩边坡的寿命,需要在边坡稳定性模型中定量描述结构面的长度和抗剪强度与岩体溶蚀速率的关系。由于试验条件的制约,本研究未开展溶蚀试验,重在提出灰岩边坡服役寿命预测的数学模型;此处引用文献[17]中的灰岩边坡溶蚀速率作为该数学模型中的溶蚀衰减速率δD(%)。定义灰岩质量损失率Mc(%)为:

(1)

式中:m0为试样试验前的烘干质量,g;mc为试验后的烘干质量,g。

文献[17]为了模拟酸雨侵蚀灰岩的实际情况,通过循环试验模拟了某地年降雨量为1 000 mm的灰岩溶蚀过程,得出方解石含量为88.03%的灰岩年质量损失率为1.821%。因此,本研究岩体溶蚀速率引用该文献数据,即δD取1.821%。

图1为西南地区某灰岩边坡示意图,该地区年降水量常介于600～1 100 mm之间,常年经受雨水和大气的溶蚀作用。图1中b为该灰岩边坡滑体的坡顶宽度,m;h为灰岩边坡的高度,m;假设边坡沿着结构面AB滑动,其中BD为结构面AB的贯通段L1,AD为结构面AB的非贯通段L2;θ为结构面AB的倾角,(°)。

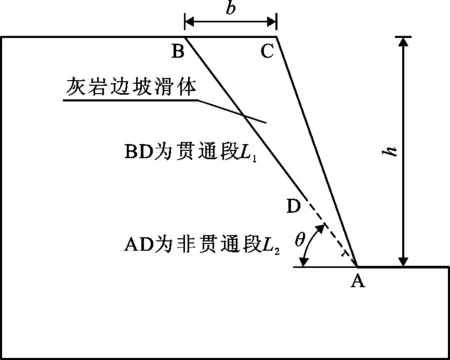
图1 灰岩边坡示意图

2.1 边坡滑体的受力分析

该灰岩边坡滑体的受力分析如图2所示。

图2 灰岩边坡滑体受力分析示意图

灰岩边坡滑体的重心处作用有自重力Gr,灰岩边坡结构面AB的贯通段BD上作用有法向力N1和切向力S1;灰岩边坡结构面AB的非贯通段AD上作用有法向力N2和切向力S2。

2.2 服役n年后灰岩边坡结构面贯通段和非贯通段的有效长度

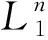
(2)

(3)

式中:L为灰岩边坡中结构面AB的长度,m;k为灰岩边坡中结构面AB的贯通率;δD为灰岩边坡岩体的溶蚀速率,%;n为灰岩边坡的服役年限,a。

2.3 服役n年后灰岩边坡结构面的抗剪参数

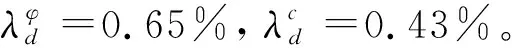
(4)

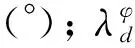
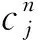
(5)

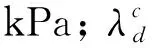
3 灰岩边坡长期服役的稳定性非线性数学规划模型

灰岩边坡服役寿命问题是一个复杂的力学和数学问题,灰岩边坡服役寿命与溶蚀速率直接相关,两者的关系呈现出高度非线性,力学建模较为复杂;求解灰岩边坡的服役寿命是一个数学极大值问题,建立灰岩边坡服役寿命的数学规划模型的思路为:(1)拟定灰岩边坡服役寿命计算的基本参数;(2)进行灰岩边坡滑体的受力分析;(3)根据溶蚀速率计算服役n年后灰岩边坡结构面贯通段和非贯通段的有效长度;(4)根据结构面贯通段的抗剪参数溶蚀衰减速率计算服役n年后结构面贯通段的抗剪参数;(5)建立灰岩边坡长期服役的稳定性非线性数学规划模型;(6)求解灰岩边坡的服役寿命。

3.1 目标函数

设灰岩边坡的服役寿命为目标函数,并求其最大值,目标函数如下:

Maximize:n

(6)

式中:n为灰岩边坡的服役年限,a; Maximize表示“使最大”。

3.2 服役n年后灰岩边坡滑体的平衡方程

服役n年后灰岩边坡滑体的水平方向的平衡方程为:

N1sinθ-S1cosθ+N2sinθ-S2cosθ=0

(7)

式中:N1、S1分别为作用于单位宽度灰岩边坡结构面AB的贯通段BD上的法向力、切向力,kN/m;N2、S2分别为作用于单位宽度灰岩边坡结构面AB的非贯通段AD上的法向力、切向力,kN/m;θ为灰岩边坡结构面AB的倾角,(°)。

服役n年后灰岩边坡滑体的竖直方向的平衡方程为:

N1cosθ+S1sinθ+N2cosθ+S2sinθ-Gr=0

(8)

Gr=γrhb/2

(9)

式中:Gr为作用于单位宽度灰岩边坡滑体重心处的自重力,kN/m;h为灰岩边坡的高度,m;b为灰岩边坡滑体的顶部宽度,m;γr为灰岩边坡岩体的容重,kN/m3。

3.3 结构面屈服条件

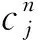
(10)

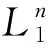
服役n年后灰岩边坡结构面AB的非贯通段AD受法向力N2、切向力S2以及非贯通段凝聚力cr的作用,屈服条件为:

(11)

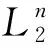
附加约束条件为:结构面AB的贯通段BD所受N1为压力,S1为沿结构面向上的抗滑力,即N1≥0、S1≥0;结构面AB的非贯通段AD所受N2为压力,S2为沿结构面向上的抗滑力,即N2≥0、S2≥0。

3.4 灰岩边坡长期服役的稳定性非线性数学规划模型

将目标函数、灰岩边坡滑体的平衡方程、贯通段和非贯通段的屈服条件以及附加约束条件集成,得到灰岩边坡长期服役的稳定性非线性数学规划模型如下:

(12)

求解灰岩边坡长期服役的稳定性非线性数学规划模型的流程如图3所示。

图3 灰岩边坡服役寿命计算流程图

4 算例分析

4.1 本文算法与有限元法计算结果对比

本文算法采用数值解析方法来计算灰岩边坡的服役寿命,思路如下:

(1)假定边坡沿着结构面滑动,并对结构面贯通段和非贯通段进行受力分析,结构面贯通段、非贯通段有效长度按照公式(2)、(3)扩展;结构面抗剪参数随着服役年限的衰减按照公式(4)、(5)计算。

(2)根据边坡滑体的平衡方程以及屈服条件、附加约束条件,通过“序列二次规划法”逐步迭代,直至收敛,最后输出最优解。

为了验证本文算法的正确性,用有限元软件Optum G2采用强度折减法计算并与本文算法进行对比,有限元法计算灰岩边坡服役寿命的思路如下:

(1)在有限元中,常以结点位移作为基本未知量,并对每个单元根据分块近似的思想,假设一个简单的函数近似地表示单元内位移的分布规律,再利用力学理论中的变分原理建立结点力与位移之间的力学特殊关系,得到一组以结点位移为未知量的代数方程,从而求解结点的位移分量,然后利用插值函数确定单元集合体上的场函数。经过迭代,近似解最终将收敛于精确解。

(2)强度折减法的基本思想是通过一定的折减系数不断折减岩土体的强度指标,得到一组新的强度参数,然后将折减后的强度参数指标重新代入到计算模型中计算,根据Mohr-Coulomb准则,如果边坡仍然处于稳定状态,继续增大折减系数,直到边坡发生失稳破坏时对应的折减系数即为所求状态下边坡的安全系数。

选取前文所述西南地区某灰岩边坡进行计算分析,如图4所示。

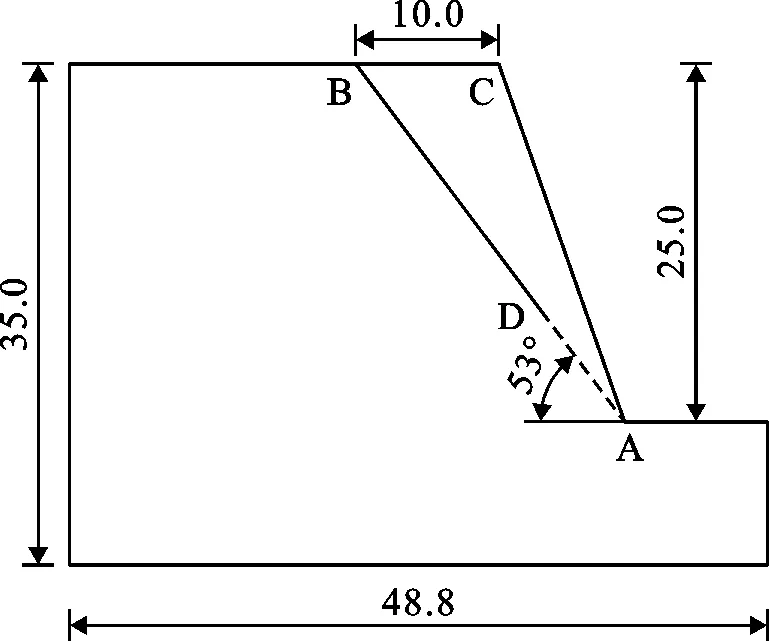
图4 灰岩边坡计算实例示意图(单位:m)

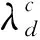
表1 实例灰岩边坡服役寿命本文算法计算结果

图5为有限元网格图。本算法假设灰岩边坡滑体沿着结构面AB的延长线剪切破坏,为了验证假定破坏面位置的正确性,选取结构面贯通率分别为0.70和0.85的灰岩边坡做对比,有限元法与本文算法灰岩边坡破坏面的计算结果对比如图6、7所示,图中椭圆内为灰岩边坡坡脚处有限元计算破坏面和假定破坏面的放大图,其中虚线为本算法假定的破坏面,实线为有限元强度折减法计算的破坏面,贯通率为0.70时,两破坏面间的夹角为13°,贯通率为0.85时,两破坏面间的夹角为10°;对于不同贯通率,边坡破坏面的位置略有偏差,且计算结果表明贯通率越大,误差越小,由于到该边坡服役失效时结构面非贯通段仅剩不到2 m,因而破坏面之间的偏差可以忽略。

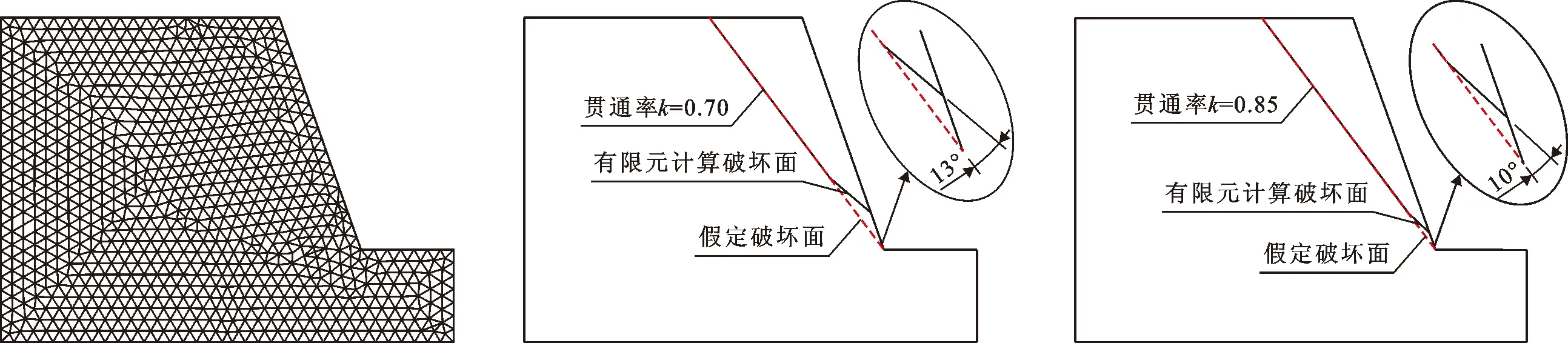
图5 有限元模型网格划分 图6 贯通率为0.70的破坏面对比图 图7 贯通率为0.85的破坏面对比图

本算法除了可以得到边坡服役寿命和破坏面外,还可以计算得到灰岩边坡的稳定性安全系数F。求解安全系数时,只需要将边坡稳定性安全系数设为目标函数,并求其最大值。即将目标函数式(6)改写为:

Maximize:F

刚入行的时候我就发现，没有必要融入进去。我倒不如做个村子里搜集信息的人，或者是来自火星、对一切都充满好奇的人。幸好，这世界上到处都是倾诉欲泛滥的人，他们都想把自己的故事告诉你，想把你不知道的东西告诉你。

(13)

此外,改变屈服条件形式,将公式(10)、(11)改写为:

(14)

(15)

式中:F为边坡稳定性安全系数,其他符号意义同公式(10)、(11)。

最后,将边坡服役年限n作为变量,将公式(13)、(14)、(15)代入公式集(12)中,得到公式集(16)为求解灰岩边坡稳定性安全系数的非线性数学规划模型,即可计算出各个服役年限下灰岩边坡的稳定性安全系数。

(16)

表2为本文提出的基于溶蚀速率的灰岩边坡长期服役稳定性非线性数学模型与有限元强度折减法计算的安全系数对比。每隔5 a输出1个边坡安全系数,当服役60 a时边坡失稳破坏,边坡安全系数平均相对误差为2.47%,其中前15 a相对误差较大,原因是边坡初期阶段的溶蚀速率较中后期更慢。通过对比表明本算法是正确、有效的。

表2 灰岩边坡安全系数两种方法计算结果对比

4.2 本文算法可行性的验证分析

为了进一步验证本文算法的可行性,以实例灰岩边坡作为计算模型,其几何参数以及抗剪参数溶蚀衰减速率保持不变,将岩体和结构面的抗剪参数作为变量(基准参数同表2),取岩体的初始凝聚力cr分别为500和300 kPa;岩体初始内摩擦角φr分别为40°和30°;结构面AB的贯通段BD的初始凝聚力cj分别为40和30 kPa;结构面AB的贯通段BD的初始内摩擦角φj分别为32°和22°,将本文灰岩边坡长期服役的稳定性非线性数学规划模型的计算结果与有限元强度折减法的计算结果进行比较,得到的边坡安全系数F随服役年限n的变化曲线如图8所示。

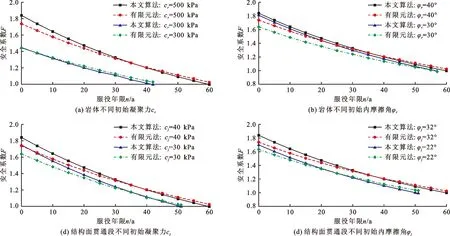
图8 岩体和结构面不同抗剪参数下边坡安全系数随服役年限的变化曲线

分析图8可知:(1)灰岩边坡岩体初始凝聚力cr=500 kPa时的服役寿命为59.68 a,cr=300 kPa时的服役寿命为41.59 a。两种不同初始凝聚力所呈现的边坡稳定性变化规律基本一致,边坡安全系数随着服役年限的增加逐渐降低,两种方法计算结果较为吻合。

(2)灰岩边坡岩体初始内摩擦角φr=30°时的服役寿命为56.42 a,岩体初始凝聚力对边坡稳定性的影响较初始摩擦角更为明显,两种不同初始内摩擦角所呈现的边坡稳定性变化规律基本一致,边坡安全系数随着服役年限的增加逐渐降低,两种方法计算结果较为吻合。

(3)灰岩边坡结构面贯通段初始凝聚力cj=30 kPa时的服役寿命为50.88 a,两种不同初始凝聚力所呈现的边坡稳定性变化规律基本一致,边坡安全系数随着服役年限的增加逐渐降低,两种方法计算结果较为吻合。

(4)灰岩边坡结构面贯通段初始内摩擦角φj=22°时的服役寿命为50.09 a,两种不同初始内摩擦角所呈现的边坡稳定性规律基本一致,边坡安全系数随着服役年限的增加逐渐降低,两种方法计算结果较为吻合。

在基准参数的基础上改变边坡抗剪参数后,本文算法计算的安全系数与有限元法计算结果的相对误差平均值见表3,表中参数变量均为单一变量,即其余参数均保持为基准参数不变。由表3可知,改变4个参数后,按本文算法计算的安全系数与有限元法计算结果的相对误差平均值介于1.57%～4.97%之间,误差处于可接受范围之内。因而本文算法对灰岩边坡长期服役寿命的预测具有可行性。

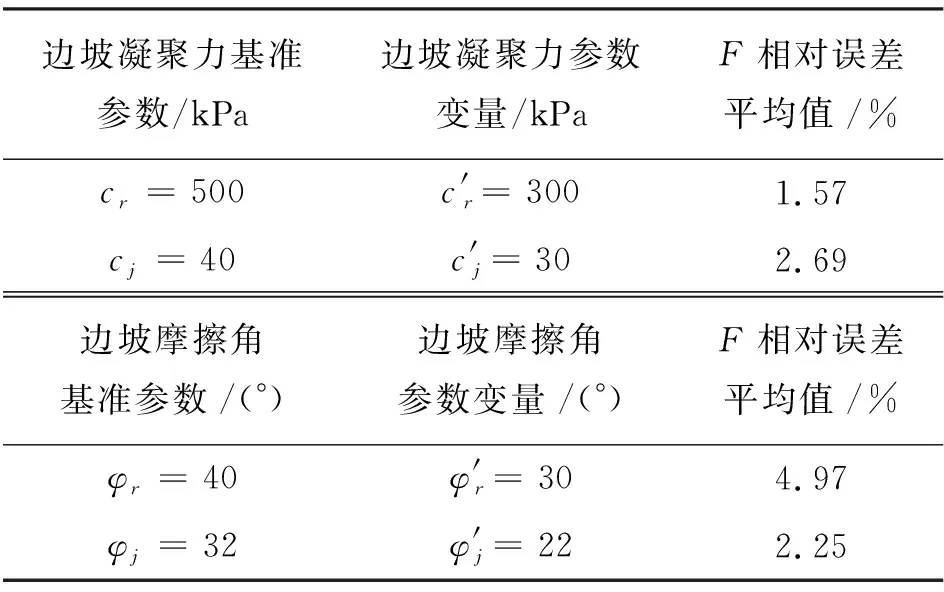
表3 本文算法计算的安全系数与有限元法计算结果的相对误差平均值

5 讨 论

(1)本研究基于灰岩边坡的溶蚀速率以及裂隙的溶蚀发展程度,采用稳定性非线性数学规划模型来计算灰岩边坡服役寿命的最优解,相对于有限元法,本文提出的算法避免了繁琐的刚度矩阵计算,可以直接求得解析解,从而提高了计算效率,丰富了灰岩边坡服役寿命年限的计算方法。

(2)相对于有些学者提出的疲劳断裂寿命计算方法,本文方法理论严谨、程序编制容易、计算精度较高。如文献[14]需要通过计算危岩结构面能承受暴雨状态下裂隙水压力交变作用的次数与特定地区暴雨发生次数平均值的比值,进而得出危岩服役年限;文献[15]通过计算岩土抗剪强度参数可以承受交通疲劳荷载循环次数与初始疲劳设计寿命的比值,得出边坡的服役寿命,然而,交通荷载循环次数统计以及荷载大小均为边坡服役寿命计算准确性的重要影响因素,需要精确数据的支持。所以上述两个文献中提出的方法都具有一定的局限性,本文提出的稳定性非线性数学规划模型可以通过最优化算法直接得到灰岩服役寿命的最大值,预测的灰岩边坡服役寿命更为准确。

(3)随着科学技术的发展,许多工程的核心问题最终都归结为优化问题,本文所采用的优化方法能够为解决一些工程问题提供新思路。

6 结 论

(1)本文从灰岩边坡长期溶蚀速率的角度,采用优化方法,将灰岩边坡服役寿命作为目标函数,根据溶蚀速率和抗剪参数衰减速率计算服役n年后灰岩边坡结构面贯通段和非贯通段的有效长度以及结构面的抗剪参数;结合边坡滑体的平衡方程以及结构面贯通段和非贯通段的屈服条件,建立灰岩边坡长期服役的稳定性非线性数学规划模型,能够较为精确地计算出灰岩边坡的服役寿命,有效评价灰岩边坡的长期安全性,解决了灰岩边坡服役寿命预测这一难题。

(2)本文所提出的算法与有限元法的计算结果相比,不同服役年限下安全系数平均相对误差为2.47%;在分别改变灰岩边坡的4种抗剪参数下,边坡安全系数平均相对误差介于1.57%～4.97%之间,表明两种算法计算结果高度吻合,验证了本文计算方法的可行性。

(3)本文以灰岩边坡为研究对象,由于条件制约,未进行灰岩的溶蚀试验,根据相关文献确定的灰岩溶蚀速率与实际情况可能存在一定的偏差,今后尚需进一步完善。