基于层次分析法和模糊理论的小型水库土石坝安全评价

2023-09-11周海怡李淑祎蔡先锋申屠毅刘桢义章振华林颖典

水资源与水工程学报 2023年4期

周海怡, 李淑祎, 蔡先锋, 申屠毅, 刘桢义, 章振华, 金洁, 林颖典

(1.浙江大学海洋学院, 浙江舟山 316021; 2.杭州鲁尔物联科技有限公司, 浙江杭州 311121; 3.浙江省杭州市余杭区林业水利局, 浙江杭州 311115)

1 研究背景

我国水库大坝多为混凝土坝和土石坝,其中土石坝在施工组织、建材质量、养护管理等方面的特点,使其在长期服役过程中容易出现材料老化变质、结构异常破坏、坝基异常渗漏等安全隐患[1]。对于传统的中小型水库土石坝的安全评价技术,一方面人工巡检不仅费时费力,还存在主观误差等不可量化的因素;另一方面监测设备成本较高,且局部布设仪器不能满足整体监测的需求[2]。全国水库大坝安全评价工作内容、方法及标准主要以《水库大坝安全评价导则》( SL 258—2017,简称《导则》)[3]为参照,但现有指标体系在复杂的水库大坝安全评价场景中仍存在主观性和模糊性较强的缺陷。

近年来许多学者采用层次分析法、风险评估法等方法,对小型水库土石坝进行结构安全状态评价,以提升水库大坝安全监管水平,保障大坝长期稳定运行[4-7]。梁文娟等[8]通过调研陕西省10个地市共172座小型水库,建立了基于层级分析法的物元可拓评价模型,为小型水库的标准化运行管理提供了科学建议。江超等[9]梳理了小型水库大坝安全鉴定基本程序以及在安全鉴定过程中存在的典型问题,并提出改善小型水库安全评价方法和提高工程安全鉴定质量的工作建议。孙玮玮等[10]构建了小型水库除险加固评估指标体系和方法,通过工程案例验证了方案的可行性。Daud等[11]利用层次分析法评估了大坝溃坝影响因素,着重分析了结构因素、人为因素和自然因素,分析结果与依据溃坝准则计算的评价等级一致,并对大坝渗漏导致溃坝问题的运维管理提出了建议。Juliastuti等[12]基于目视和仪器检测识别坝体损伤,利用层次分析法并辅以专家调查法确定大坝修复优先级,并应用于大坝工程实例,对大坝损坏修复工作提出了建议。

以上安全评价体系与计算方法均基于传统安全评价进行了优化改善,但在针对小型水库土石坝特点的评价程序繁简程度和量化定性指标等方面有待进一步完善与提高。本文首先建立小型水库土石坝安全评价指标体系,然后采用层次分析法计算指标权重,并结合模糊理论修正使权重值更客观,根据模糊综合评价的最大隶属度原则,得到小型水库土石坝的安全状态评价结果。

2 水库大坝安全评价指标体系

水库大坝安全评价影响因素之间相互作用,评价体系又具有多层次、多因素的结构形式,因而在综合评价时难以一次性比较出指标间的重要程度[13]。因此,构建典型且能够全方位反映实际需求的安全评价指标体系有利于分析水库大坝安全状态的演化趋势[14]。

依据《导则》《水库大坝安全管理条例》(2018年修订,简称《条例》)[15]以及《水库大坝安全鉴定办法》(水建管[2003]271号文件,简称《办法》)[16]的要求,通过多次组织人员进行管理档案收集、工程现场巡查,本文基于资料分析、数值模拟和计算,针对指标体系鲜明的层次性和模糊性,建立水库大坝安全评价因素集,构建多级评价指标体系,明确了指标之间的从属和并列关系。

2.1 小型水库土石坝评价因素集

将水库大坝安全评价指标体系从上至下分为目标层、准则层和指标层3级,本文的评价对象为灌溉型小型水库土石坝,本着系统性、层次性和可操作性的原则,初选《导则》规定的6个指标作为评价体系的准则层。针对小型水库土石坝的类型、工程等别以及枢纽工程和主要建筑物,结合健康大坝的内涵和影响因素,对评价指标体系进行修改和完善[17-19],共设立23个评价指标。其评价指标体系如图1所示。

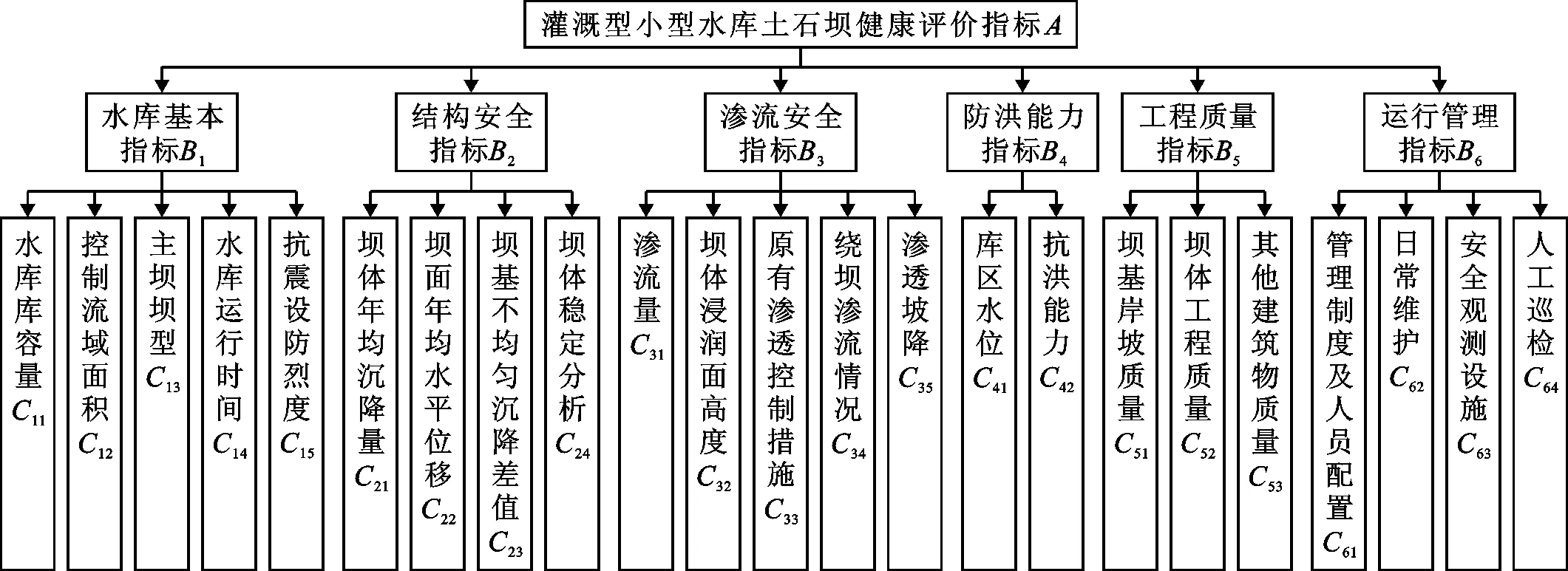
图1 灌溉型小型水库土石坝安全评价指标体系

2.2 小型水库土石坝评价评语集

在《导则》中,水库大坝安全综合评价被划分为A、B、C 3类,分别对应工程质量合格、运行管理规范的一类坝,运行性态基本正常、但存在安全隐患的二类坝,工程存在严重质量缺陷、不能正常服役的三类坝。但是,《导则》的分类较为简单,所给出的判断依据不够细致[20]。本文将水库大坝安全综合评价等级划分为4类,提供更为细致详尽的划分依据,并能够根据评价结果提出安全隐患处置建议和方案。本文将评价评语集划分为公式(1)所示的4个等级,对应的评价含义分别为:“健康”“基本健康”“较不健康”“不健康”。

U={u1,u2,u3,u4}={Ⅰ,Ⅱ,Ⅲ,Ⅳ}

(1)

3 小型水库土石坝模糊综合评价

3.1 模糊理论与评分标准

经典集合理论(set theory)认为某个因素是否属于某个等级只有真或假两种情况[21],而水库大坝安全状态评价的等级具有一定的模糊性和不确定性,不易直接划分为好或坏两种情况,模糊理论(fuzzy theory)充分补充了经典集合理论的不足,在进行安全状态评价时,因素集对评语集的隶属度充满连续区间,即{0,1}→[0,1][22]。在灌溉型小型水库土石坝安全状态的影响因素中,需要量化单因素指标的评语集等级区间,便于构建隶属函数,再利用专家评分所给的量化值,得到计算插值点。常规的安全状态评价所使用的专家调查法大多忽视了专家自身缺陷和专业程度[23],本文在进行专家评分时,构建由15人组成的专家评分小组,参与调查的专家包括大坝设计人员、建筑工程师、运维管理人员,并综合考虑小组内专家的工龄、职称等因素,确保评分过程的客观性和评分结果的可靠性。根据公式(1)所示评语集,将专家评分区间划分为:等级1为健康,评分[100, 80);等级2为基本健康,评分[80, 60);等级3为较不健康,评分[60, 40);等级4为不健康,评分[40, 0)[24]。

3.2 构建模糊隶属度矩阵

本文采用指派法确定隶属函数(membership function),通过专家访谈和资料调研,明确水库大坝安全评价的性质,然后选用抛物型、正态型、柯西型等类型的模糊分布函数计算隶属度,构建模糊综合评价矩阵,按照最大隶属度原则,计算目标层和准则层指标的安全状态评价结果[25]。

通过专家调查法得到的指标层各指标的评分值离某一评分区间的中点越近,则对该等级的隶属度越高;离该评分区间的边缘越近,则对该等级的隶属度越低,甚至可能属于其他等级。这种特性类似于正态分布函数,故本文选用正态型分布的函数作为隶属函数[26]:

r(x)=exp[-(x-a)2/σ2]

(2)

式中:x为专家对影响因素的评分;a为各等级评分区间的中值;σ为待定参数。

若专家对影响因素的评分为中值a,则该指标的隶属度为1。若专家对影响因素的评分位于区间的两端,则表明该指标对相邻两区间的隶属度相同,均为0.5。则有:

r(x)=exp[-(x1-x2)2/4σ2]=0.5

(3)

式中:x1、x2为评分区间的端点值,将该值代入即可求得参数σ。

由于安全评价指标体系中指标的评分值越高代表该指标的安全状态评价越好,对最佳等级的隶属度越高,但不应超过1,而正态型隶属函数存在两端隶属度低于1的情况,故需对其两端进行修正,本文利用将左、右两端隶属函数分别升半梯度和降半梯度的方式,使修正后正态分布型隶属函数的隶属度恒等于1[27]。修正后的隶属函数如下:

(4)

(5)

(6)

(7)

公式(4)～(7)中,各隶属函数参数取值根据不同等级区间的端点值利用等式(3)确定,计算结果如表1所示。

表1 各等级隶属函数参数取值

在构建模糊综合评价模型的过程中,首先需要确定指标层各指标对公式(1)所示评语集的隶属度,得到各单因素的模糊子集,再经过归一化处理计算单因素隶属度矩阵(matrix of membership degree)。本文准则层6个指标Bi(i=1,2,…,6)对应的指标层各指标对评语集的模糊综合评价矩阵为Ri(i=1,2,…,6),具体形式如下:

(8)

(9)

(10)

(11)

结合利用层次分析法得到的权重向量Wi,可以得到准则层指标的模糊评价矩阵:

(12)

进一步可以计算目标层的安全状态评价结果:

(13)

最后,按照最大隶属度原则选择max{Ai}(1≤i≤4)作为最终的水库大坝安全状态评级。

4 各级指标权重的确定

层次分析法在定性决策过程中引入定量分析,以降低主观判断对决策结果的影响[28]。此外,在使用层次分析法时,构建多层评价指标体系的过程有助于决策者更加全面地考虑影响决策的因素,在计算过程中更清晰地衡量指标间的重要性优先级[29]。

在实际计算过程中,需要具有深厚知识储备和实践经验的专家作为参与决策的评价者,由专家对决策指标体系中准则层指标间以及同一准则层下的指标层指标间进行相对重要性评分,由此计算准则层和指标层指标的比较判断矩阵,然后对每个矩阵的最大特征根进行一致性检验,将通过一致性检验的指标权重值进行排序,以确定决策结果[30]。

4.1 构建比较判断矩阵

基于构建的评价指标体系(如图1)进行定性定量分析,首先需要将同一准则层的各个元素进行两两比较,计算指标间相对重要性的量化值,即比较判断矩阵,以尽可能排除决策认知的局限性对结果的影响,降低不同性质元素相互比较的困难,提高评价判断的准确度[31]。本文采用1—9标度法构建比较判断矩阵,表2列出了各标度的含义[32]。

表2 1—9标度法含义表

在灌溉型小型水库土石坝安全评价体系中,本文以工程质量综合指标B5为例,对B5的3个子指标 “坝基岸坡质量C51”“坝体工程质量C52”“其他建筑物质量C53”构建比较判断矩阵,如表3所示。同理可得准则层指标间以及同一准则层指标下的指标层各指标间的比较判断矩阵。

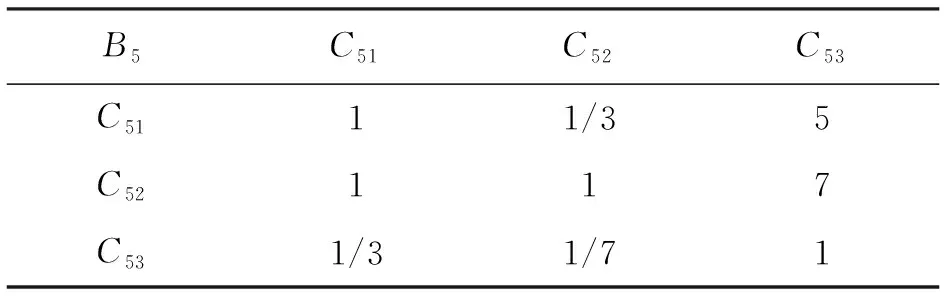
表3 B5-C比较判断矩阵

4.2 权向量计算及一致性检验

本文采用根法计算指标权重向量W,具体过程如下:

(1)比较判断矩阵中每行连乘,然后开m次方,得到向量:

(14)

(15)

(2)对W*进行归一化处理,得到权重向量:

W=(w1,w2,…,wm)T

(16)

(17)

(3)对比较判断矩阵中每列元素求和,得到向量:

S=(s1,s2,…,sm)

(18)

(19)

(4)计算最大特征值λmax:

(20)

一致性检验的具体步骤如下:

(1)一致性指标CI(consistency index)

(21)

式中:n为矩阵阶数,λmax为矩阵的最大特征值。

(2)随机一致性指标RI(random index)

利用RI衡量CI的大小,通常情况下,其值与比较判断矩阵的阶数呈正相关。

(22)

(3)一致性比例CR(consistency ratio)

CR≤0.1表示矩阵满足一致性要求,CR>0.1表示矩阵达不到一致性要求,需要重新构建矩阵。CR的值按照下式进行计算:

(23)

按如上所述流程,对每个比较判断矩阵计算权重并进行一致性检验。

5 实例分析

康门水库位于浙江省杭州市余杭区良渚街道安溪村,属东苕溪水系,东苕溪流域及测点分布如图2所示。

图2 东苕溪流域及测点分布图

水库的来水面积为4.647 km2,主流长度为4.06 km,水库总库容为142.99×104m3,是一座承担下游约133 hm2农田灌溉任务的小(1)型水库。康门水库于1960年竣工,2003年经余杭区林业水利局技术认定为二类坝,同年进行标准化建设,2014年在下游坝坡几处渗漏点处设置砂石反滤体。康门水库正常蓄水位为24.67 m,相应库容为101.46×104m3,设计洪水位为26.21 m,校核水位为26.29 m。主坝原为均质坝,坝长为168.5 m,坝顶宽度为8.5 m,最大坝高为17.3 m,坝顶高程为27.32 m,副坝位于主坝左侧300 m处,原为一山坳,副坝坝顶高程为28.69 m,坝顶宽度为3.0m。

5.1 各因素隶属度计算

依据建立的灌溉型小型水库土石坝大坝安全综合评价方法,在进行专家评分时遵循2.1节提出的标准规则。依据《导则》《条例》和《办法》的要求,借鉴灌溉型小型水库土石坝科学管理的专家知识和实证资料,确定指标层各指标的评分条件和专家评分,如表4所示。

表4 康门水库大坝各项安全评价指标得分

在计算渗流量时,使用Abaqus软件计算康门水库大坝的渗流孔隙水压力云图(如图3),分析大坝渗流场的变化情况,取大坝中渗流水体饱和区域与非饱和区域的边界线为浸润线,下游边界节点上单位时间流出云图模型的流体体积即为渗流量,经计算得到单位宽度的渗流量为0.128 L/(s·m)。

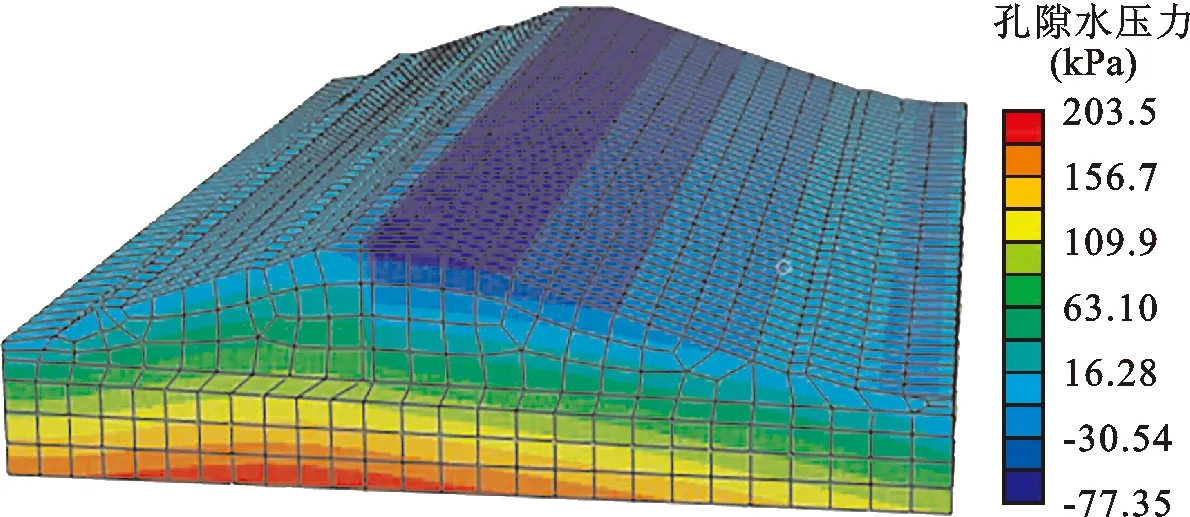
图3 康门水库大坝渗流孔隙水压力云图

在确定渗透坡降的评分条件时,依据《水利水电工程地质勘察规范》(GB 50487—2008)(2022年版)[33]附录G的规定,通过分析康门水库地勘资料的颗粒分析成果,并参考类似水库大坝坝体土的试验成果,宏观判断康门大坝土的渗透变形形式为流土型,流土型临界比降Jcr采用由极限平衡理论所得的太沙基公式计算,康门水库大坝安全系数取值为2,则渗透坡降为[J]=Jcr/2=0.501。

根据公式(2)～(7)计算指标层各指标对各评价等级的隶属度,结果见表5。

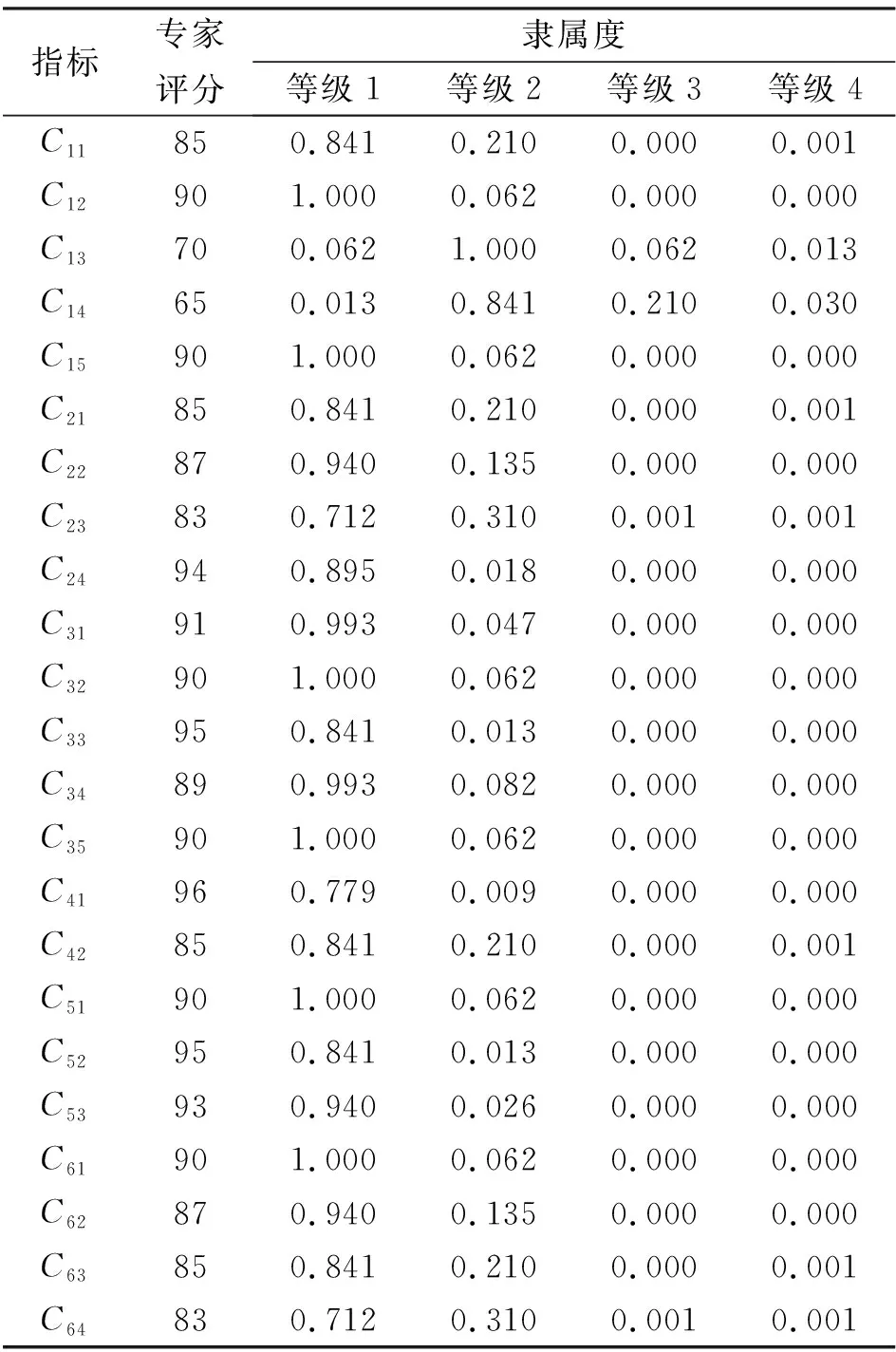
表5 康门水库大坝各项安全评价指标的专家评分及单因素隶属度

5.2 各指标权重计算

基于构建的灌溉型小型水库土石坝健康评价指标体系(图1),利用1—9标度法构建比较判断矩阵,再根据公式(14)～(22),计算得到的准则层和指标层指标权重如表6所示。

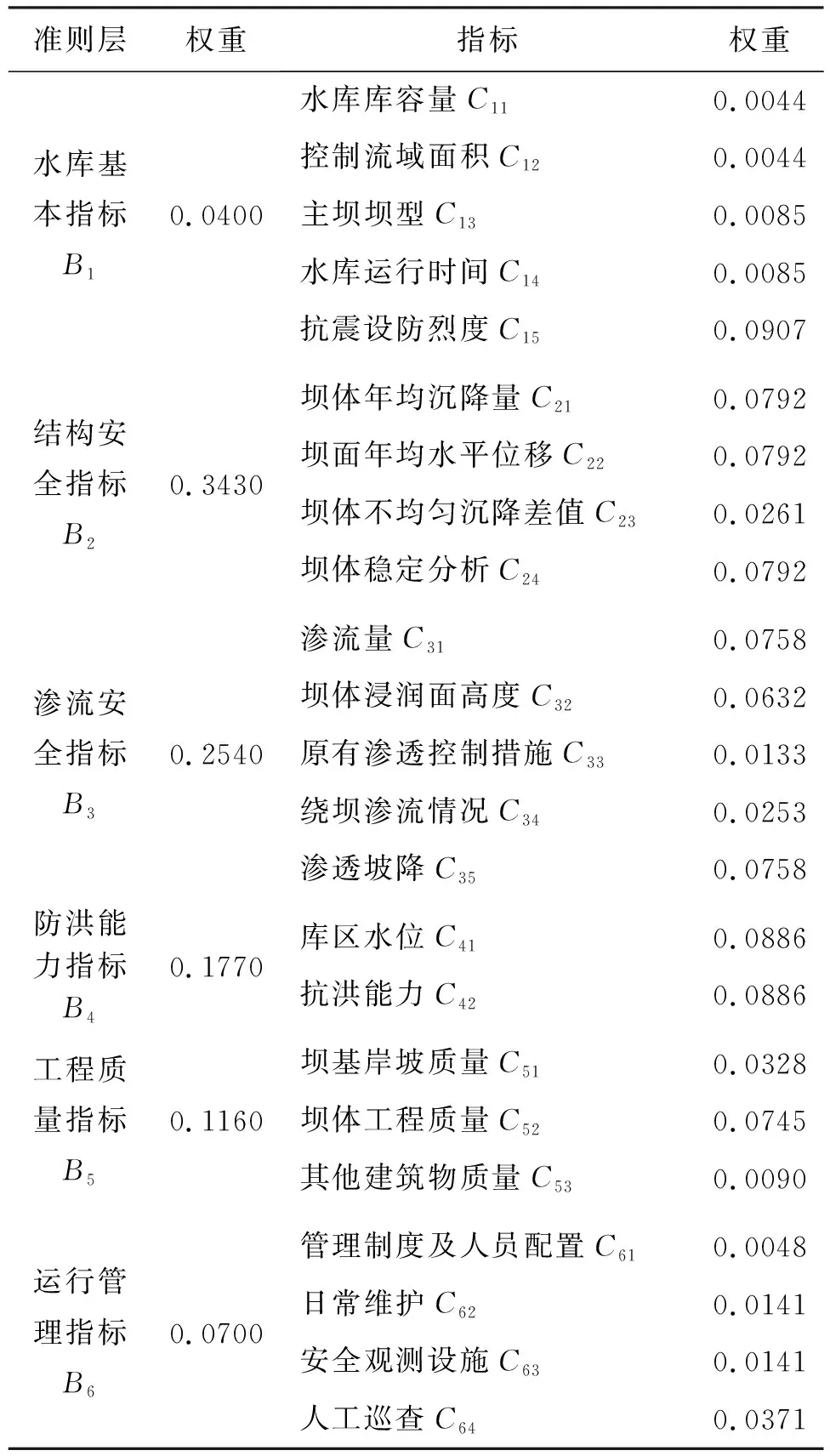
表6 康门水库大坝安全评价指标体系准则层和指标层指标权重

5.3 大坝安全状态评价结果

利用专家评分、单因素隶属度和准则层指标权重向量,按照公式(8)～(12)计算目标层评价结果:

根据最大隶属度原则,结合公式(1)所构建的评语集等级区间,康门水库大坝结构处于安全状态,模糊综合得分为:0.645×90+0.306×70+0.035×50+0.006×20=82.15。根据公式(8)～(12)计算康门水库大坝安全评价体系准则层6个指标的模糊综合评价结果如图4所示。

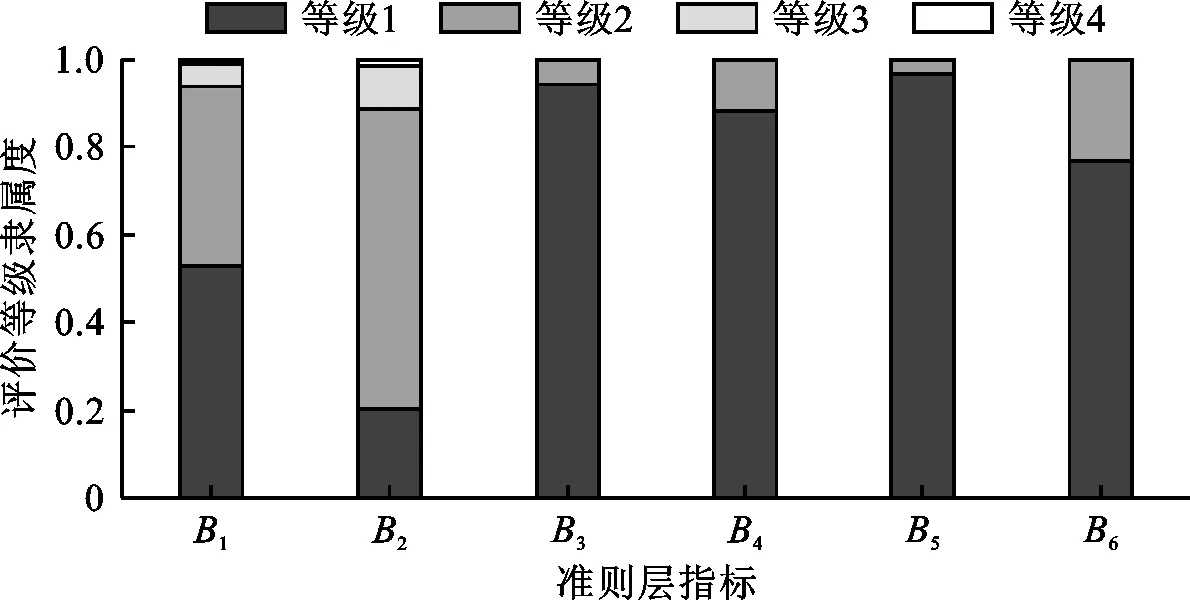
图4 康门水库大坝安全评价体系准则层各指标模糊综合判断评价结果

5.4 讨论

本文的实例分析结果如图4所示,结合最大隶属度原则可以直观地看出,水库基本指标B1的等级1隶属度值最大,表明康门水库大坝的该指标情况为“健康”;结构安全指标B2的等级2隶属度值最大,表明大坝的该指标情况为“基本健康”,但坝体存在不均匀沉降和稳定性问题,同理可得其余指标的安全状态。基于准则层指标与指标层指标的模糊综合评价结果,通过分析大坝外观、结构安全情况和运行管理条件等现场检查情况,表明大坝结构运行正常,但仍存在结构承载力退化、材料破损和性能降低等问题,对大坝结构的长期安全稳定运行构成威胁,建议及时对溢洪道和防浪墙进行修缮,并加强大坝日常管理,定期检查工程设施,建立水库安全鉴定和运维监管的技术档案库。

本文在进行小型水库土石坝的安全健康评价时,按照《导则》规定设置目标层、准则层和指标层,验证了灌溉型小型水库土石坝的安全评价需要充分考虑大坝的抗滑稳定性和渗流性安全,并且需要保证溢洪道稳定和渗流量满足运行要求。许多学者也从其他角度制定安全评价指标体系,如陈曦等[24]针对无金属结构的农村地区小型水库大坝进行安全评价时,重点考虑了大坝、溢洪道、输水管涵的模糊综合评价结果;陈果[34]侧重于分析运行时间较长的土坝,对大坝变形和浸润线进行观测,提出了必要时需要整治和翻修大坝溢洪道护砌、防渗帷幕的建议。

因此,大坝安全评价指标的选择应该结合工程实际情况和未来发展需求进行修改和完善,使其更具针对性和适用性。此外,更加完善的工程资料和检测设施更有助于专家进行精确判断,避免因资料缺乏而导致的局限性。在实际工作中还应重视专家质量,因为模糊层次分析法中隶属度的计算过程对专家经验要求较高。