河湖底轴驱动翻板生态闸门静动力特性分析

陈 卫, 王 晨, 李津宇, 杨贵海, 王正中

(1.中铁水利水电规划设计集团有限公司, 江西 南昌 330029; 2.西北农林科技大学 水利与建筑工程学院, 陕西 杨凌 712100)

1 研究背景

钢闸门是水利水电工程泄水建筑物的调节咽喉,保障其安全、灵活地运行决定着整个枢纽工程和下游人民生命财产的安全[1]。

随着农业生产的发展及人类活动的加剧,流域及河湖水生态、水环境问题日益严重。针对河湖蓄水、渔业、景观设计、湿地保护等问题,合理适当地设置河湖生态闸门是非常有效的工程手段,底轴驱动翻板闸门作为一种依靠底轴转动控制开度的新型可调控溢流闸门,凭借其结构型式简单、景观效果良好、生态效益明显的优点在各类河湖生态景观建设中得到广泛应用,具有极佳的生态效应[2-5]。例如上海市苏州河河口闸工程、黄山湖边水利枢纽花山坝工程、泰州市水生态环境建设工程、苏州工业园区金鸡湖游艇码头工程等均运用了底轴驱动翻板闸门[6]。

近年来,国内外专家学者已经对底轴驱动翻板闸门的相关问题开展了一定研究,严根华[7]对苏州河河口水闸进行了有限元计算,揭示了闸门结构在不同运行工况下的变形和受力特性,并提出了优化方案;张明等[8]对闸门结构中的疲劳问题进行分析,对闸门的设计及运行提出了建议;尤宽山等[9]针对底轴驱动式翻板闸门泄流时由于泥沙淤积导致开启困难的问题,介绍了闸门的冲淤系统及深化设计;杨贵海等[10]针对该类型闸门底轴受力情况,分析了闸门结构设计时应注意的技术问题及相应的工程措施,提出了一种底轴结构最优化的设计方法;陆伟刚等[11]通过模型试验研究了多沙河流中底轴驱动翻板闸门的闸下水流流态,探究了泥沙对闸门运行的影响。

但在实际运用中,部分工程的底轴驱动翻板闸门已经出现了一些问题。分析其原因,主要在于针对该类型闸门的设计规范并不完备,存在部分未考虑到的问题。由于底轴驱动翻板钢闸门的跨度较大,在水荷载长期作用下,闸门跨中可能发生变形,导致个别闸门启闭困难。针对底轴驱动翻板闸门这一空间结构出现多方向的变形问题,仅用平面体系法对闸门进行计算设计显得不够充分,故在设计阶段,应考虑空间效应的三维有限元法。三维结构有限元静动力分析在水利工程上的应用已经比较成熟,但目前还少有应用于底轴驱动翻板闸门的设计与分析。因此,本文将针对该类型闸门的空间有限元计算流程进行研究。

CFD-CSD(computational fluid dynamics-computational structure dynamics)耦合数值模拟方法融合了计算流体动力学和计算结构动力学,随着计算机技术的发展和有限元理论的成熟,该方法已经运用到平面钢闸门、弧形钢闸门等常见水工钢闸门的有限元计算中[12-14],其计算流程也可以为底轴驱动翻板闸门的流固耦合计算研究提供参考。

综上所述,本文根据某实际工程底轴驱动翻板闸门的受力及结构特性,采用CFD-CSD耦合的数值计算方法,进行作用在闸门上水荷载的模拟和闸门结构静动力特性的模拟[15]。首先,利用Fluent软件对作用在闸门上的水荷载特性进行模拟,得到高精度的水荷载分布;其次,采用流固耦合方法将荷载传递到闸门结构上,在有限元计算软件ANSYS中对底轴驱动翻板闸门进行静力分析,评估闸门静力安全性,同时分析闸门开度对各结构的影响,找寻最不利开度工况[16]以便为工程实际提供参考;最后,对闸门的自身动力特性进行数值模拟分析,并基于附加质量法[17]对闸门结构受水荷载状态下的动力特性进行计算,得到闸门干、湿模态的自振频率和振型,分析水体对闸门结构自振特性的影响,为底轴驱动翻板闸门设计及运行提供一些理论基础。具体分析流程如图1所示。

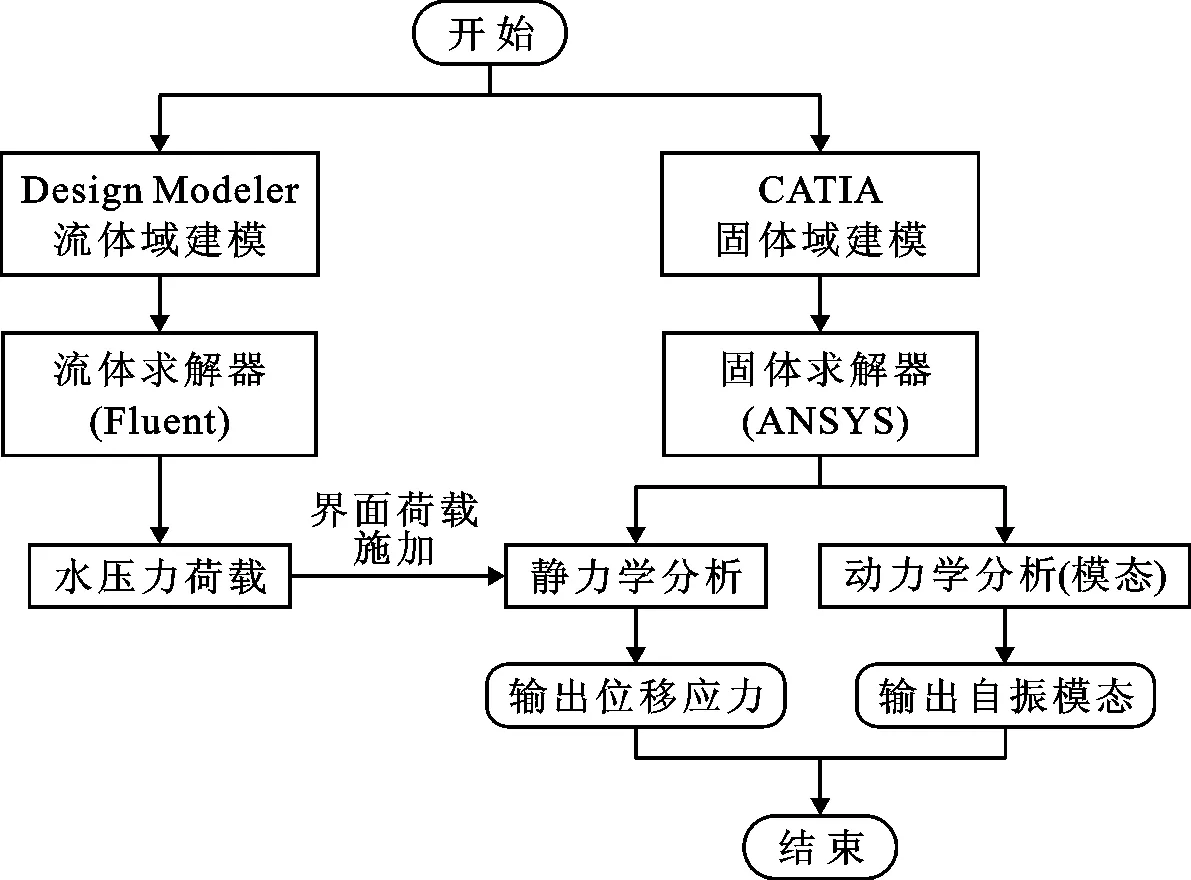
图1 底轴驱动翻板闸门静动力特性分析流程

2 数值分析理论

2.1 流场及湍流模型

在保证计算精度要求和计算自由需求的前提下,本文选择时均化求解Reynolds方程方法进行流场计算,基于有限体积法对流场控制方程进行离散。由于流体力学的基本方程适用于封闭的层流运动,当采用时均方法描述湍流运动时,需要补充新的方程才能求解,因而进一步引入涡黏模型对湍流进行更精确的模拟。闸门泄流的绕流流场可以认为是不可压流体湍流流动,实际的流动复杂多变,在边界条件不变的情况下,流动仍是不稳定的,速度等流动特性均随机变化。目前数值模拟分析计算湍流的方法多样,在工程领域应用最多的是雷诺平均法中的RNGk-ε两方程计算模型[18-19]。由于闸门顶部的流线曲率变化较大,属于大压力梯度的非定常流动,而RNGk-ε模型在ε方程中增加了一项参数来反映流动的时均变化率,考虑了分离流动和旋涡效应对水体的影响,优化了对耗散率方程的模拟,更加接近闸门区泄水绕流实际的流场特性,故选用RNGk-ε模型能更加准确地分析闸门水荷载特性。RNGk-ε模型的两方程如下[20]。

k方程:

(1)

ε方程:

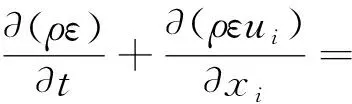
(2)

其中:

(3)

(4)

(5)

式中:ρ为流体密度,kg/m3;k为紊动能,J;ε为紊流耗散率;t为时间,s;ui、uj为流速分量,m/s;xi、xj为坐标方向分量,m;η为应力率;Cμ、σk、σε、C1、C2为常数,根据经验[20]分别取值为:Cμ=0.0845、σk=σε=1.39、C1=1.42、C2=1.68;Gk为压力生成项;μeff为湍流有效黏度系数,不同雷诺数取值不同;μ为平均流速梯度引起的湍动能k的产生项。

2.2 自由表面模型

闸门泄流过程属于典型的水气分层两相流动,且高速下泄水流在经过闸门底缘时会出现水气掺混现象,这也是闸门水荷载变化复杂的重要表征[18]。闸门水荷载特性复杂程度受水气掺混复杂程度的影响,故有必要对闸门过流区域的水气两相交换过程进行数值分析。目前用于两相流数值模拟分析的方法是VOF法(volume of fluid method)[21],即通过求解水体单元网格中水相的体积函数来追踪自由表面,该方法的优势在于计算量小且实现难度低,并且能处理自由表面变形大的流体计算问题,是适用于闸门泄流流场计算的方法。VOF模型的连续性方程为:

(6)

式中:αw为水的体积分数;t为时间,s。

RNGk-ε模型在引入VOF模型之后,计算中的流体密度ρ和黏度系数μt相应地有所变化,即:

ρ=αwρw+(1-αw)ρα

(7)

μt=αwμw+(1-αw)μα

(8)

式中:ρw和ρα分别为水体和气体的密度,kg/m3;μw和μα分别为水体和气体的黏度系数。

2.3 结构动力响应分析

闸门结构的动力响应分析采用瞬态动力学计算,计算中对闸门结构采用直接积分法进行瞬态动力学分析,具体采用隐式算法中的Newmark法进行计算。结构的瞬态动力学结构体系的运动方程为:

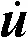
(9)

模态分析的主要目的是研究闸门的固有动力特性,不考虑水体作用时闸门结构体系的运动方程可以简化为:

([K]-ω2[M]){φ}={0}

(10)

式中:ω为结构体系的自振频率,Hz; {φ}为特征向量,与结构体系的模态相关。

由于闸门结构的主要工作环境是在水中,并且在研究闸门振动时,需要考虑附加水体的作用,因而在闸门湿模态分析中,在公式(10)的基础上增加附加水体质量矩阵[Mp],则考虑水体作用时闸门结构体系的运动方程为:

{[K]-ω2([M]+[Mp])}{φ}={0}

(11)

3 工程概况及有限元模型

3.1 工程概况及物理模型

某泄水闸设置4个孔口,单个孔口宽度为38 m,每个孔口的闸门结构采用底轴驱动翻板闸门型式。闸门最大转角为90°,考虑水头超高,门顶挡水高度最大值为0.5 m,单扇闸门分别由4扇中门和2扇边门组成,门体结构包括7根水平横梁、15根纵梁、2根边梁顶隔板以及过水结构,采用结构钢Q235B。底轴外径为1 800 mm,内径为1 640 mm,采用结构钢Q345B。该工程底轴驱动翻板闸门结构平面图如图2所示。

图2 实例工程底轴驱动翻板闸门结构平面图(单位:m)

该闸门计算跨度为38 m,考虑到数值模拟计算量较大且该闸门为对称结构,故为提升有限元计算效率,建立二分之一模型进行分析计算。底轴驱动翻板生态闸门过闸水流流速相对较小,过闸水流流经闸门之后在下游消力池内消能,同时下游水深不大,产生的波浪对闸门振动影响较小[22],但是考虑到下游出口边界设置为静水压力出口,要求水流不能有较大的紊动,因而模型下游段长度也不能太短。综上,闸前上游段近似取5倍闸门的等高长度,总长为30 m;下游段近似取8倍闸门等高长度,总长为50 m。闸门物理模型采用专业几何软件CATIA建立,门体部分采用创成式外观设计建立壳结构,底轴及支座部分采用零件设计建立为实体结构,流场部分也建立为实体结构。闸门结构及闸门上下游段物理模型如图3所示。

“哈哈，你马国平还算有点良心！还知道一连吃肉，给我们救护队分点汤！”汪队长的脸色和悦起来，“说真的，看你们冲锋在前，我们救护队员很是佩服。”

3.2 有限元模型网格划分与边界条件

在物理模型基础上进行离散,建立有限元模型,由于本工程模型比较复杂且根据计算需要,对流场和闸门结构分别进行网格划分。根据ANSYS软件中各单元性质,闸门门体结构采用壳单元SHEll63进行模拟,底轴、支座及拐臂部分采用实体单元solid65进行模拟。选取100 mm作为闸门金属结构网格划分尺寸,以闸门全关工况为例,最终网格划分单元数为552 491,节点数为879 459。闸门几何结构和网格划分如图4所示。根据底轴驱动翻板闸门在静态挡水工况下的工作状态,在拐臂与启闭机连接处施加固定约束(fix support);在底轴与支座连接处施加圆柱约束(cylindrical support),并释放径向转动自由度模拟底轴转动情况;在支座与地基相连处施加固定约束(fix support);在对称轴处施加对称约束(remote displacement),约束底轴轴线方向上的平动自由度和其余两个方向的转动自由度。为考虑闸门自重,沿竖直方向施加9.81 m/s2的重力加速度,具体约束情况如图5所示。

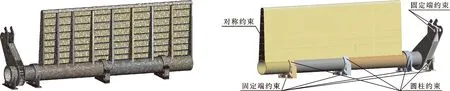
图4 闸门结构网格划分 图5 闸门结构约束设置

3.3 强度和刚度判别准则

为确保闸门的结构安全,需要对闸门进行强度和刚度安全评价。根据《水利水电工程钢闸门设计规范》(SL 74—2019)[23],在强度方面,根据闸门面板的受力特点,其达到材料强度极限后仍能承受继续增大的荷载,具有一定的强度储备,因此需对面板的实际容许应力进行折算,其折算公式为σZ≤α[σ]。由于本工程闸门区隔长宽比大于3,故取α=1.5,相应的面板折算应力为251.85 MPa;在刚度方面,对于露顶式工作闸门,其主梁的最大挠度与计算跨度的比值不应超过1/600,该工程中闸门跨度为38 m,按照规范要求,最大容许挠度为63.33 mm。

4 结果与分析

4.1 静力计算结果

对闸门施加水荷载以及重力加速度后进行有限元计算,图6为闸门全关工况的等效应力云图及位移云图。由图6可以看出,闸门最大等效应力为200.79 MPa,由于应力集中出现在面板和底轴连接处(图6(a));闸门位移大小分布总体呈现中部大于两端、顶部大于下部的规律,最大位移为47.703 mm,发生在闸门顶部中点处。

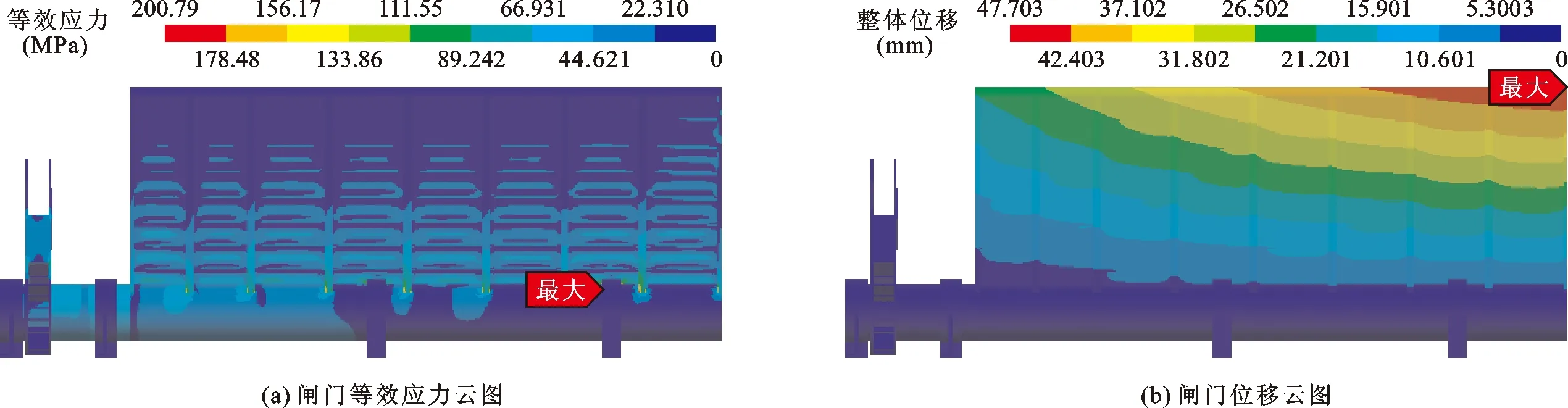
图6 闸门全关工况下等效应力及位移云图

根据计算结果,该工况下闸门的强度和刚度均满足规范要求[23]。而后在全关工况的基础上以10°为旋转角度差值旋转门体,以模拟闸门开启时的不同开度状态。各开度下闸前水头均设置为超过闸门顶部0.5 m,模型约束条件均与全关工况相同,对不同开度下闸门等效应力、底轴切应力以及位移进行计算,计算结果分别见表1、2,闸门各构件等效应力和位移随开度的变化趋势如图7所示。由计算结果和变化趋势可以看出,最大应力由于应力集中均位于面板处;最大位移均位于闸门中心纵梁腹板处;随着开度的增大,闸门整体和各构件的等效应力和位移、底轴切应力均呈现减小趋势。

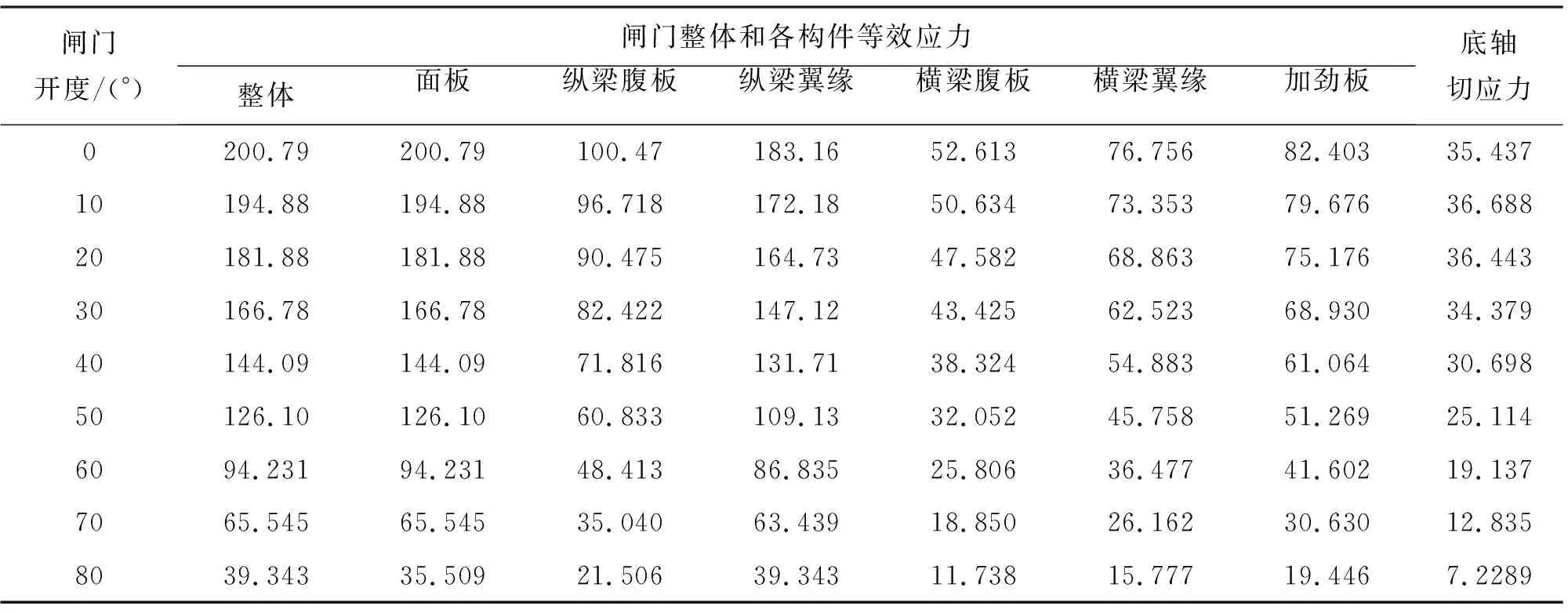
表1 不同开度下闸门整体和各构件等效应力以及底轴切应力计算结果 MPa

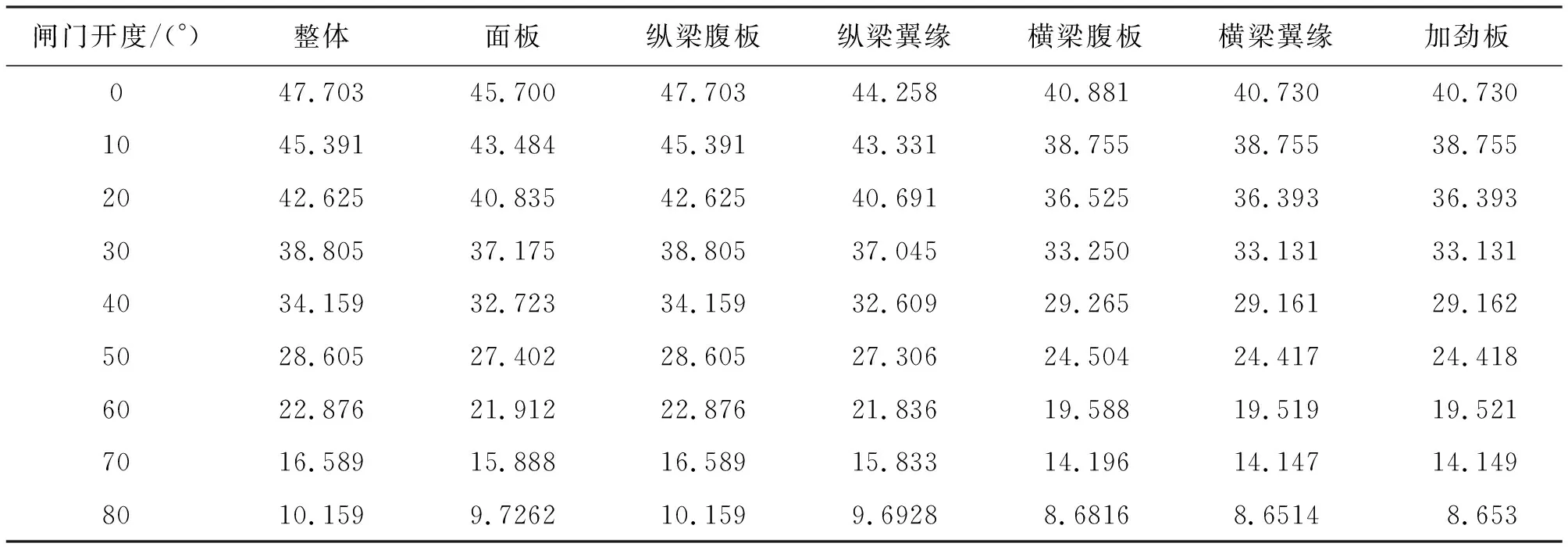
表2 不同开度下闸门整体和各构件位移计算结果 mm

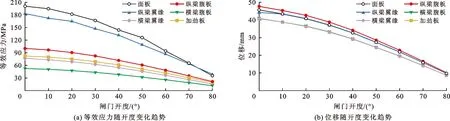
图7 闸门各构件等效应力和位移随开度的变化趋势

4.2 闸门自振特性分析

采用大型有限元分析软件ANSYS Workbench平台对平面闸门进行模态分析。干模态分析采用Modal模块,湿模态分析采用 Modal Acoutstics 模块。干模态分析中,约束条件及接触条件与结构分析相同;湿模态分析中,在干模态模型基础上,在上游建立水体模型并设置流固耦合交界面,水体模型的长度会影响闸门的自振频率,当水体长度为闸门高度的3倍以上时,水体长度的变化对闸门振动的影响可忽略[24-25],故选取闸前30 m建立水体,湿模态几何模型如图8所示。

图8 湿模态几何模型(单位:m)

将建立的几何模型导入Workbench进行网格划分和模态分析,主要考虑结构几何形状、研究对象和约束作用的范围,网格划分时兼顾计算精度与求解效率[26-27]。通过网格精度试算分析,最终干模态有限元模型共生成1 105 076个单元和1 757 284个节点,湿模态有限元模型共生成1 267 878个单元和4 342 631个节点。对闸门结构在空气中和水中的结构动力特性进行分析,分别得到不同工况下的干、湿模态特性,即结构的自振频率和振型。干、湿模态前十阶自振频率及对比见表3,前六阶干、湿模态振型云图见图9。

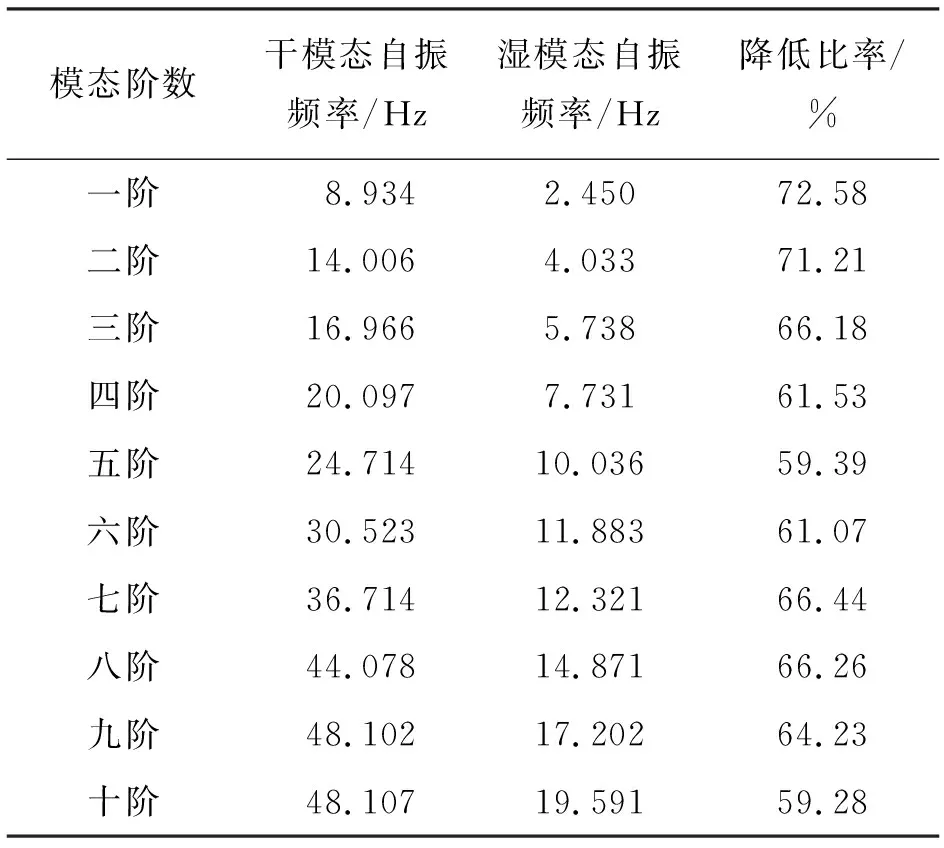
表3 闸门干湿模态前十阶自振频率

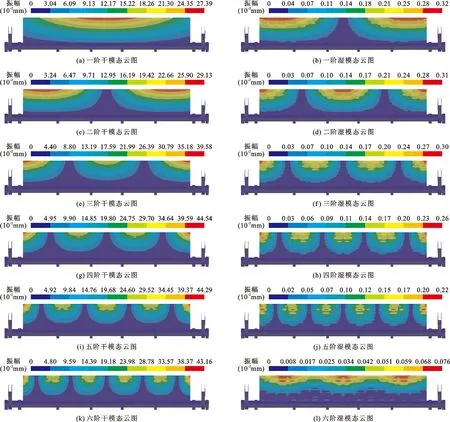
图9 闸门各阶干、湿模态振型图

由表3和图9可以看出,在无水体作用时一阶振动频率为8.934 Hz,振型为门顶顺水流方向弹性弯曲振动,门顶中心位置振动幅值最大;二～六阶振动频率分别为14.006、16.966、20.097、24.714、30.523 Hz,振型均为门顶两侧顺水流方向弹性弯曲振动且门顶两侧位置振动幅值最大。在有水体作用时,一阶振动频率为2.450 Hz,振型为门顶两侧顺水流方向弹性弯曲振动,门顶靠近两侧位置振动幅值最大;二阶自振频率为4.033 Hz,振型为门体中部及两侧的顺水流方向弹性弯曲振动,门顶中部及两侧均有较大的振动幅值;三、四、五阶自振频率为5.738、7.731、10.036 Hz,振型均为门顶两侧顺水流方向弹性弯曲振动,门顶两侧位置振动幅值最大;六阶自振频率为11.883 Hz,振型为门顶中心及靠近两侧部分的顺水流方向弹性弯曲振动并有较大的振动幅值。

由于几何结构的原因,底轴驱动翻板闸门振幅最大处多发生于闸门顶部,方向均为顺水流方向,且闸门低阶模态自振频率均同水流脉动频率(1～20 Hz)有交集,在设计时需要在闸门顶部采取相应的措施抑制其振动,例如可以增加加劲板和加劲肋,增大门顶构件尺寸;从模态云图来看,水体对闸门振动发生位置产生影响,且同阶干、湿模态对比来看,在水体影响下闸门振动部位明显增多;从干、湿模态自振频率数值对比来看,水体可以降低闸门自振频率,降低比率介于59.28%～72.58%,一、二阶的自振频率降低了70%以上,可见水体对低阶模态影响更为显著,在动力分析时水体效果不容忽视。

5 讨 论

本文针对河湖生态底轴驱动翻板闸门静动力特性进行了系统研究。根据前人研究成果[7,22,28-29],本研究的计算结果与实验及数值模拟结果相符。杨贵海等[10]基于底轴驱动翻板闸门的实际受力情况,通过计算为该门型的设计提供了一些理论基础;刘进国[30]和李旭等[31]从制作工艺的角度对底轴驱动翻板闸制造的关键点进行了研究,这些研究对有限元计算分析过程中精确考虑各类材料的特性与初始缺陷有很大的参考价值。胡涛勇等[32]以某实际工程底轴驱动翻板闸为例,基于流固耦合方法,对该闸门在水流作用下的受力情况进行了分析,并给出了最不利工况,与本文的数值模拟结果相符,证明了本文结果的合理性。

目前关于河湖生态底轴驱动翻板闸门各项特性的研究还不多。本文根据实际工程设置情况,对该类型闸门结构的静动力特性进行了模拟计算与分析,可为实际工程设计及运行状态的安全评价提供参考。但本文模型计算中仍做了部分简化,针对多孔闸门的情况并没有充分考虑。如何进行更加精确的模拟计算以及该类型闸门相关的生态问题还有待于进一步深入研究。

6 结 论

(1)根据底轴驱动翻板闸门的几何型式及受力特性,提出底轴驱动翻板闸门CFD-CSD耦合数值计算的方法流程,并以某实际工程为案例进行计算,在设计水头条件下对闸门结构的静力特性进行分析,表明各开度工况下该工程闸门设计均满足规范要求,可为后续该闸门的静动力特性分析及深入研究提供参考。

(2)底轴驱动翻板闸门的最大应力和最大位移均出现在闸门全关闭工况,最大应力和最大位移均随闸门开度的增大而逐渐减小,故全关闭工况为静态挡水不利工况,在设计与后续校核中应重点关注全关闭工况的结构应力与变形特性。

(3)根据闸门动力特性分析,底轴驱动翻板闸门振动多发生于闸门顶部且为顺水流方向振动,在设计时需对闸门顶部采取抑制振动措施以防止闸门发生疲劳破坏;该类型闸门整体刚度较小,闸门自振频率受水体影响显著,水体可使闸门的自振频率降低60%～70%,因此,在计算动力特性时,水体作用不容忽视,需要考虑流固耦合效应,进一步对闸门进行结构响应分析。