基于EMD-LSTM耦合模型的趵突泉岩溶地下水水位预测应用

侯金霄, 黄林显, 胡晓农, 钱 永, 邢立亭, 韩 忠, 梁 浩

(1.济南大学 水利与环境学院, 山东 济南 250022; 2.中国地质科学院 水文地质环境地质研究所, 河北 石家庄 050061; 3.山东省第六地质矿产勘查院, 山东 威海 264209; 4.山东省国土空间生态修复中心, 山东 济南 250014)

1 研究背景

趵突泉属于济南市四大泉群之一,位于济南泉域北部中心地区。自20世纪50年代以来,趵突泉流量总体呈衰减趋势[1],近几年在降水量较少时期,趵突泉水位常在黄色警戒线(水位降至28.15 m)波动,甚至逼近于红色停喷预警线(水位降至27.60 m)[2-3]。因此,准确预测趵突泉水位对济南泉域保护和岩溶地下水的开发利用具有重要意义。但由于岩溶含水介质具有强烈的不均一性和各向异性,使其水位动态体现出非线性及非平稳波动特征,使得水位预测结果易产生较大误差[4]。过去几十年间,国内外学者探讨了各种方法来进行岩溶地下水水位预测,如:赵丹等[5]在对兰村泉域岩溶地下水水位埋深进行预测时选用了灰色GM(1,3)模型(grey model (1, 3)),平均预测准确率为87.79%;郭艺等[6]通过构建时间序列分析法对趵突泉水位进行预测,发现当采用逐日数据进行短时间序列预测时具有较高的精度;张郑贤等[7]构建了差分整合移动平均自回归(autoregressive integrated moving average, ARIMA)模型对济南趵突泉地下水水位进行预测,结果表明该模型预测精度优于灰色模型。陈奂良等[8]对趵突泉水位进行预测时,构建了多个BP(back-propagation)神经网络预测模型,预测结果证明加入GA(genetic algorithm)或Levenberg-Marquardt训练方法的神经网络模型具有更高的预测精度。以上研究虽然探讨了不同方法在岩溶地下水水位预测中的应用,但均存在一定的局限性:GM模型法预测时易受到地下水系统随机性的影响,造成中长期预测精度较差;时间序列类模型仅是对历史数据变化趋势的简单拟合,无法考虑外部因素(如降水、开采量等)变化带来的影响;ARIMA模型易受数据波动影响,在对岩溶地下水水位预测时存在较大的局限性;BP神经网络仅为浅层神经网络,不具备长时间记忆功能,通常只适用于短时间序列地下水水位的预测[9]。

深度学习方法在近年来发展迅速,长短期记忆(long short-term memory,LSTM)神经网络模型由于具有长时间记忆功能并能有效解决梯度爆炸问题而得到广泛应用[10-11]。闫佰忠等[12]对泰安市岱岳区地下水水位进行预测时建立了单、多变量LSTM模型及BP模型,并通过对比得出多变量LSTM模型的预测精度更好。但LSTM神经网络模型存在对具有非平稳波动特征的时间序列(如岩溶地下水水位)预测精度低、尤其是在数据突变处预测误差较大的问题。

综上所述,本文采用一种基于经验模态分解(empirical mode decomposition,EMD)和LSTM神经网络的岩溶地下水水位EMD-LSTM耦合预测模型,该耦合模型已在河流水量水位预测、降水量预测、洪水预测等方面得到有效应用[13-15]。EMD-LSTM耦合模型首先利用EMD将不平稳的岩溶地下水位数据分解为有限个较平稳的分量,有效降低了原始时间序列的非线性及波动性特征;其次构建了多变量LSTM预测模型,利用与岩溶地下水水位动态密切相关的降水量、气温值、最高气温值、最低气温值和水汽压值(月平均数据)对分解后的平稳分量分别进行预测;再累加重构各分量预测结果,实现对岩溶地下水水位的预测。

2 数据来源与研究方法

2.1 研究区及数据来源

济南市位于鲁中山地与鲁北平原的过渡带,地势南高北低,南部边界由太古代变质岩为主的泰山余脉区域构成,东部以东坞断裂为界,西部以马山断裂为界,北部边界以奥陶纪、第四纪石灰岩为主。因受地形影响,济南市地下径流沿地形坡向自南向北流动,从南部补给区到北部排泄区均有泉水出露,其中以上升泉趵突泉最为有名[16]。趵突泉所在区域水文地质状况如图1所示。

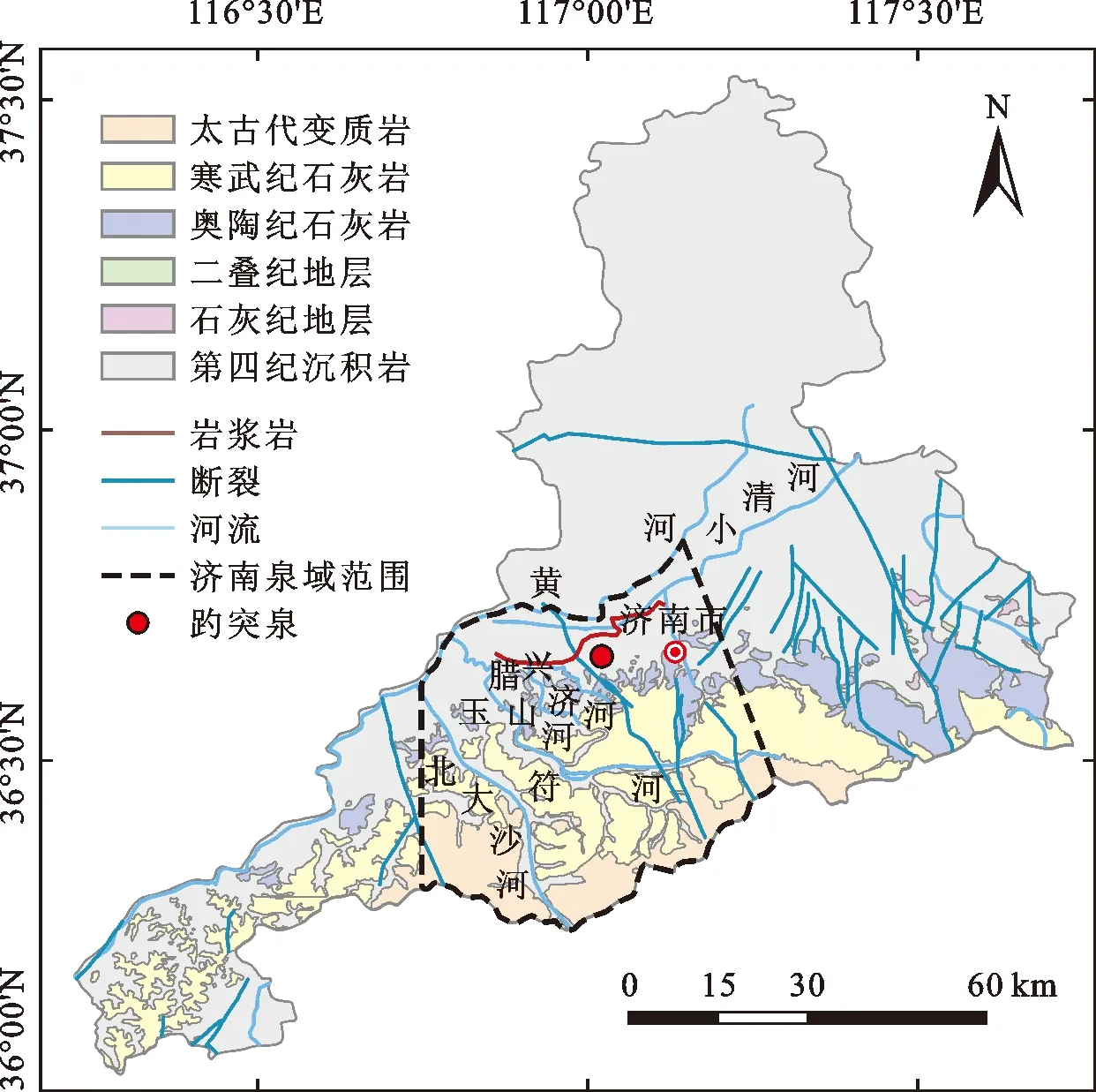
图1 趵突泉区域水文地质状况

据前人研究可知,济南岩溶地下水的动态变化与降水量、气温和水汽压等气象要素紧密相关[17-18]。因此分别选取表征地下水补给项动态变化的降水量和表征地下水排泄项动态变化的气温(包含月平均气温值、月最高气温值和月最低气温值)、水汽压作为地下水水位预测模型的输入数据。本文利用趵突泉2012年5月至2021年12月的月均水位及同时间段的月均气象数据作为预测模型的研究数据,其中水位数据来自于济南市城乡水务局网站(http://jinan.gov.cn),气象数据来自于中国气象科学数据网(http://data.cma.cn)。降水量和地下水水位的动态变化如图2所示。

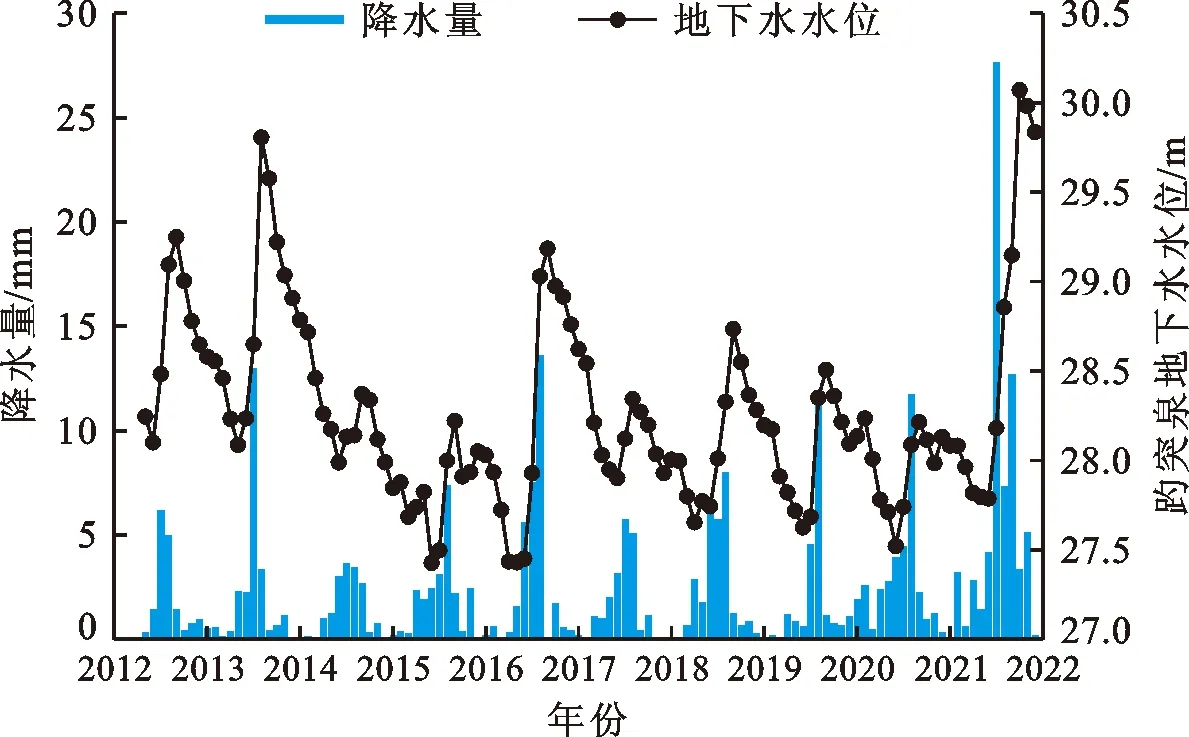
图2 2012年5月至2021年12月研究区降水量及地下水水位动态变化

通过图2可以看出,二者动态变化基本一致,均表现出明显的周期性(周期为12个月),以上动态特征说明降水是含水层的主要补给来源。

选用地下水水位数据与气温、降水和水汽压值进行互相关分析,分析结果如图3所示,其中最大时滞值为20个月。根据图3中虚线之间的95%置信区间检验的时滞值可以看出,水位的动态变化分别滞后于气温、降水、水汽压2～3个月、2～3个月、1～2个月时其相关系数最大。以上分析说明,岩溶地下水水位的动态特征主要受各气象要素的影响,因此可以利用气象要素对岩溶地下水水位进行预测。

2.2 经验模态分解

经验模态分解(EMD)是一种新型信号分解方法,该方法自适性强,能够依据原始信号本身的特征,在不需要设置基函数的前提下对其进行处理[19-20],这也使得EMD非常适用于对非平稳和非线性特征数据的前期处理[21-22]。EMD的本质是将不平稳的原始序列分解为有限个较平稳波动的序列,包括本征模函数项(intrinsic mode function, IMF)和残余项,从而降低原始序列的复杂程度[23]。EMD的算法步骤如下:

首先输入原始信号x(t),根据三次样条及所识别出的所有极大、极小值点绘制极大、极小值包络线,并计算二者平均值m1(t),用x(t)减去m1(t)得到较低频率的新信号h1(t)。

此时判断通过以上步骤获得的h1(t)信号是否能满足IMF分量确定的假设条件,满足时h1(t)成为可以获取的第一个IMF分量;如无法满足则将得到的h1(t)作为新的待分解序列返回上一步骤进行处理,再得到一个新分量h2(t),然后对h2(t)做同样的判断和处理。假设经过K次后求得的结果满足定义,则求得的第一项IMF分量C1(t)为:

(1)

r1(t)为原始信号中减去一个高频信号的新信号,其计算公式如下:

r1(t)=x(t)-C1(t)

(2)

重复上述步骤n次,直到得到第n阶IMF分量Cn(t)以及余量rn(t)。最终的EMD可以表示为:

(3)

2.3 长短期记忆神经网络

LSTM神经网络模型由Hochreiter等[24]于1997年提出,具有长时间记忆功能,能够有效解决梯度爆炸问题。一个LSTM单元包括遗忘门(forget gate)、输入门(input gate)和输出门(output gate)3个门[25]。LSTM模型计算流程如下:

(1)遗忘门。决策删除不重要的信息,其计算公式如下:

ft=σ(Wfxt+Ufct-1+bf)

(4)

(2)输入门。和tanh函数共同控制输入多少新信息,其计算公式如下:

it=σ(Wixt+Uict-1+bi)

(5)

(3)输出门。控制输出多少信息,其计算公式如下:

ot=σ(Woxt+Uoct-1+bo)

(6)

(4)3个门控系统ft、it、ot组合公式为:

st=ft⊙St-1+it⊙tanh(Wsxt+Wsct-1+bs)

(7)

ht=ot⊙tanh(st)

(8)

式中:ft、it、ot分别为遗忘门、输入门、输出门;Wf、Wi、Wo、Uf、Ui、Uo为权重项;bf、bi、bo为偏置项;σ为激活函数; tanh为双曲正切激活函数;st表示cell单元; ⊙表示矩阵以元素相乘。

2.4 EMD-LSTM耦合模型

本文所采用的EMD-LSTM耦合模型的算法流程如图4所示。

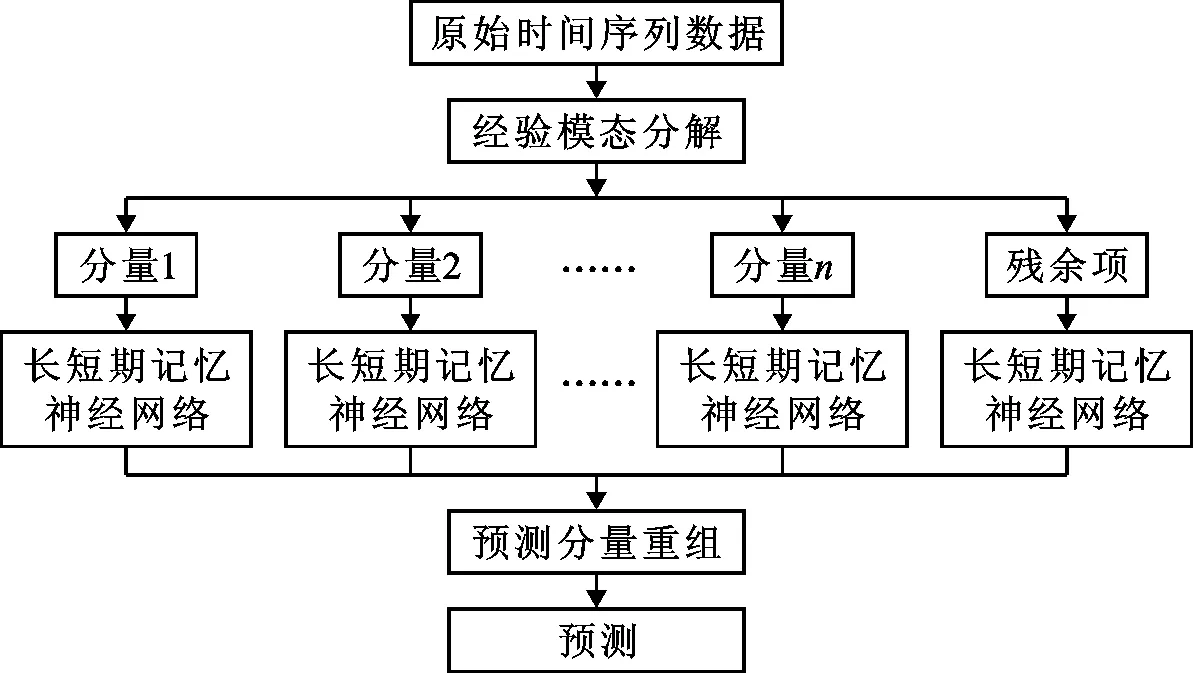
图4 EMD-LSTM耦合模型算法流程图

具体步骤如下:

(1)对岩溶地下水水位数据进行经验模态分解,得到有限个趋势项和一个残余项,将不平稳的水位数据分解为有限个较平稳波动的分量,从而降低原始序列的复杂程度,实现序列平稳化。

(2)构建多变量LSTM神经网络预测模型,将密切影响研究区地下水水位动态变化的降水量(补给项)和气温值、水汽压值(排泄项)作为输入项对各平稳分量分别进行预测。

(3)累加步骤(2)中的预测结果获得地下水水位预测值。

2.5 模型评价指标

为了评估所构建EMD-LSTM模型的预测精度,采用均方根误差RMSE作为评价指标,其值越接近于0,表示模型的预测精度越高。RMSE定义为:

(9)

3 结果与分析

3.1 经验模态分解及结果

利用经验模态分解法对2012年5月至2021年12月趵突泉岩溶地下水月均水位数据进行分解,将不平稳的地下水水位值分解为有限个平稳波动的分量,其中包含4个IMF分量和1个残余项,分解结果见图5。

图5 2012年5月至2021年12月研究区岩溶地下水月均水位经验模态分解图

由图5可知,岩溶地下水水位数据经EMD后,分量1的频率最高、波动性最强,随着分解阶数的增加,分量的频率不断变小,分量2、3、4及残余项呈现出峰值减少、频率降低、坡度变缓的规律,并逐渐趋于平稳。因此经EMD后,水位数据的非平稳性大幅降低,能够有效减少水位波动性带来的预测误差。

3.2 LSTM模型构建

本文所构建的LSTM模型为3层多变量神经网络模型,每层神经元个数为80个。由前文互相关分析可知,地下水水位在滞后气象要素1～3个月时相关性最大,因此采用前两个月气象数据对当月地下水水位进行预测。本次研究选用2012年5月至2021年12月趵突泉区域月均数据,包括降水量、气温值、最高气温值、最低气温值和水汽压值作为LSTM神经网络模型输入数据,并将训练集和预测集按照大致4∶1的比例进行划分(如表1所示)。同时,为验证EMD-LSTM预测模型的有效性及精确性,分别将其与未进行EMD的单一LSTM模型和差分整合移动平均自回归模型ARIMA进行对比。ARIMA模型是一种时间序列预测分析方法,其通过参数估计和拟合逼近观测值来建立数学模型,以此来实现对输入序列的评价预测。

表1 LSTM神经网络模型训练和预测集划分

3.3 结果分析

(1)训练集结果分析。EMD-LSTM耦合模型、LSTM神经网络模型和ARIMA模型对训练集的预测结果RMSE值分别为0.261、0.307和0.329 m,可见3种模型中EMD-LSTM耦合模型的RMSE值最小,说明其与岩溶地下水水位的拟合效果最佳。

(2)预测集结果分析。EMD-LSTM耦合模型对预测集水位各分量的预测结果如图6所示。通过对比各分量的预测曲线可以发现,分量1的预测曲线与原始数据曲线拟合度较低,预测效果最差,分析其原因主要是由于分量1作为高频分量,具有较强的不平稳性,从而导致LSTM神经网络模型对其难以获得较精准的预测结果,而分量2、分量3、分量4和残余项的波动性均显著降低,因此其预测效果较好。由此可以进一步看出,通过EMD将波动性较强的水位数据分解为平稳性更高的分量数据能够显著提高LSTM模型的预测精度。

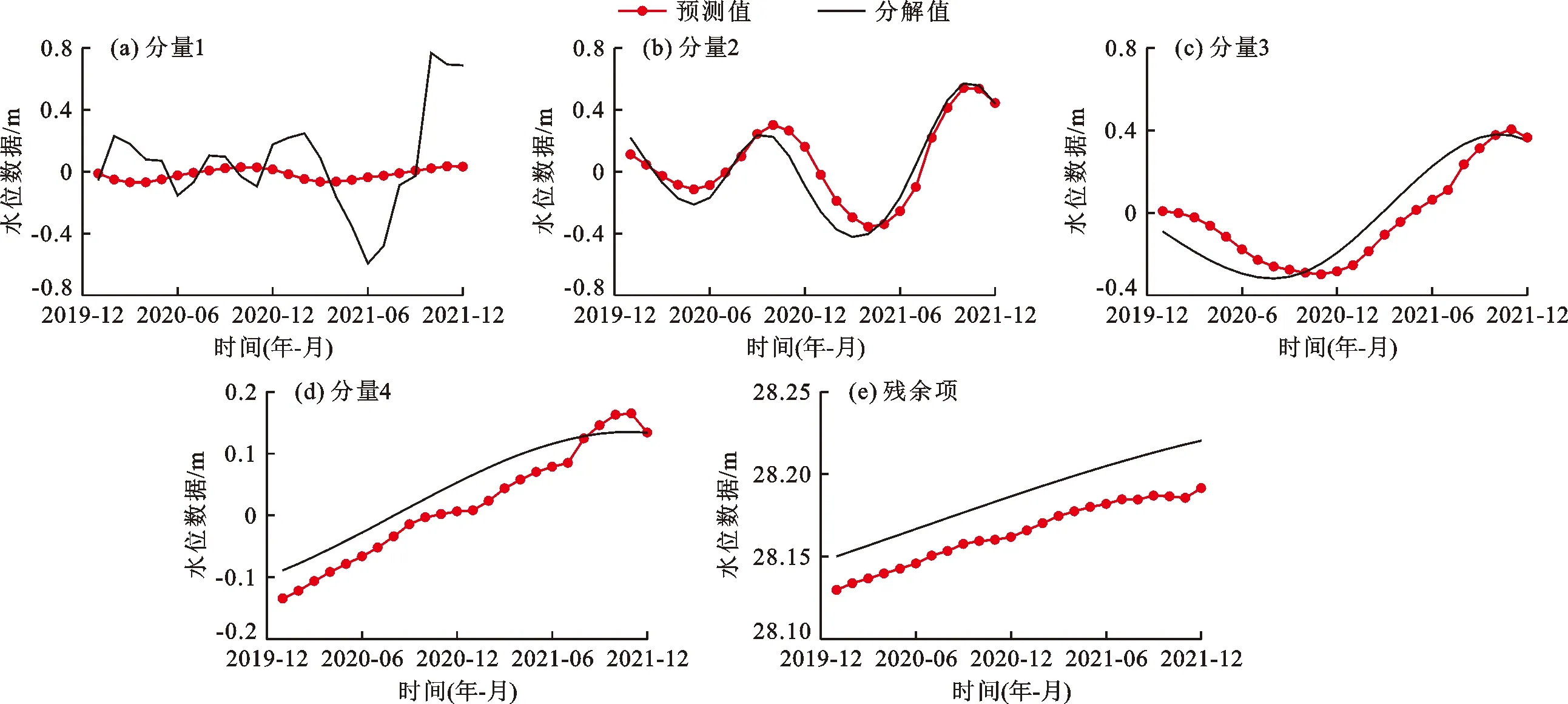
图6 EMD-LSTM耦合模型对预测集水位各分量的预测结果

将4个分量和1个残余项的预测结果进行累加,获得地下水水位数据的预测值。EMD-LSTM耦合模型、LSTM神经网络模型和ARIMA模型预测结果的RMSE值分别为0.290、0.402和0.724 m,表明EMD-LSTM耦合模型的预测误差最小,预测效果最好,其次为单一LSTM神经网络模型,ARIMA模型的预测效果最差。

3种模型的地下水水位预测值与观测值动态曲线对比如图7所示。由图7可以看出,EMD-LSTM耦合模型和单一LSTM神经网络模型预测得到的地下水水位变化曲线与实际观测曲线变化较为一致,分析其原因是由于这两种模型的输入变量均与水位变化密切相关,充分考虑了补给和排泄两方面多种因素的影响,因此能够有效提高预测精度。而ARIMA模型仅是对历史数据趋势的简单拟合,未考虑外部因素的影响,因此造成预测误差较大。此外,由于经EMD后水位分量的波动性显著降低,使得EMD-LSTM耦合模型相较于单一LSTM神经网络模型在水位突变处也能实现较好的拟合,与实际水位的波动趋势更加接近。

图7 3种模型的地下水水位预测值与观测值动态曲线对比

以上结果说明,EMD-LSTM耦合模型通过EMD将不平稳的岩溶地下水水位原始序列分解为有限个较平稳的波动序列,能够有效减少水位数据的非线性和不平稳波动特征,从而显著提高LSTM神经网络模型的预测精度。

3.4 讨 论

孙虹洁等[26]利用LSTM模型对济南市岩溶地下水水位进行预测时,得出该模型能够较为准确地实现水位预测,但是在水位突变处误差较大的结论。本文通过构建EMD-LSTM耦合模型进行岩溶地下水水位预测,利用EMD有效减小水位波动带来的影响,从而提高预测精度,并与单一LSTM神经网络模型、ARIMA模型预测结果进行对比,取得了一些有益成果,但仍存在一些问题值得进一步讨论:

(1)受数据收集困难的限制,本研究仅收集到2012年5月至2021年12月的趵突泉区域月均地下水水位和气象数据,相对较短的时间序列会在一定程度上影响3种模型的预测精度。

(2)本文构建的预测模型输入项包括降水量、气温值和水汽压值,没有充分考虑其他影响地下水水位动态变化的因素,如复杂赋存条件等的影响,也会对耦合模型的预测精度产生影响。

(3)在模型结构方面,本研究没有深入讨论模型构建层数以及单层神经元个数变化对预测精度的影响。

在今后的研究中,一方面需要收集更长时间序列的数据并考虑增加其他地下水水位影响因子作为模型的输入数据,另一方面还要充分考虑模型结构和参数设置对预测精度的影响,以进一步提高模型的预测精度。

4 结 论

由于岩溶地下水水位具有非线性和非平稳波动特征,造成水位预测结果易产生较大的误差。本文通过构建EMD-LSTM耦合模型,首先利用EMD将不平稳波动的水位数据分解为较稳定的4个IMF分量和1个残余项;再利用降水量值、气温值和水汽压值作为LSTM神经网络模型的输入项分别对各个分量进行预测,以此达到提高预测精度的目的。采用济南市趵突泉2012年5月至2019年12月的月均水位值和月均气象数据进行模型训练,并利用2020年1月至2021年12月的月均气象数据对地下水水位进行预测,得出以下结论:

(1)EMD-LSTM耦合模型、LSTM神经网络模型和ARIMA模型对地下水水位预测结果的RMSE值分别为0.290、0.402和0.724 m,说明EMD-LSTM耦合模型的预测精度最高,ARIMA模型的预测精度最差。

(2)EMD-LSTM耦合模型能够很好地体现出地下水水位的丰枯变化,在水位突变处也能实现较好的拟合,与实际水位动态相接近。

(3)EMD-LSTM耦合模型预测精度高的原因主要有以下两方面:一方面EMD-LSTM耦合模型能够通过EMD将不平稳的岩溶地下水水位原始序列分解为有限个较平稳的波动序列,使得水位数据的非平稳性大幅降低,有效减小了水位波动带来的预测误差,从而提高耦合模型的预测精度;另一方面,通过将与地下水水位动态密切相关的降水量(表征补给项)及气温、水汽压(表征排泄项)作为LSTM神经网络模型的输入变量,不同变量之间相互作用、相互验证,也有效提高了预测精度。