基于ASWPD-BO-GRU的月径流量预测模型

唐铭泽, 杨银科, 张菁雯

(长安大学 水利与环境学院 旱区地下水文与生态效应教育部重点实验室, 陕西 西安 710054)

1 研究背景

准确有效的径流预测对区域水资源水量安全评价、水资源的科学配置以及防洪减灾决策等均具有重要的意义。然而,受全球气候变化及高强度人类活动等因素的综合影响,径流时间序列呈现出复杂的非线性、非平稳性特征,使径流预测难度加大[1]。因此,探索高精度且可靠的径流预测模型成为现阶段径流预测领域亟需解决的现实问题。

目前常用的径流预测模型有过程驱动模型、数理统计模型和神经网络模型等。相比于过程驱动模型和数理统计模型,神经网络模型因其具有良好的非线性映射能力[2]、无需考虑水文过程的物理机制且能适应复杂时间序列数据,在解决径流预测方面有独到的优势[3-4]。

门控循环单元(gated recurrent unit,GRU)为神经网络中深度学习的代表技术之一,其对长短期记忆神经网络(long short-term memory,LSTM)模型的结构进行了改进,在保证预测精度的同时还拥有了更快的收敛速度[5-6]。然而,GRU的性能在很大程度上受模型超参数设置的影响,且由于原始径流时间序列具有一定的趋势性、周期性和随机性特征[7],使用单一模型进行径流预测会导致GRU的性能不能充分发挥和无法充分捕捉原始径流时间序列中的重要信息,在许多领域中对时间序列进行预测时也都面临着此类问题。在以往的研究中,通常有两种方法来提高GRU的预测精度:(1)使用优化算法优化模型超参数。如:使用粒子群算法、黏菌算法、布谷鸟搜索算法、麻雀优化算法、贝叶斯优化等优化算法确定模型的最优超参数[8-12]。其中贝叶斯优化(Bayesian optimization,BO)作为一种新兴的超参数优化方法,能够以较少的迭代次数获得满意的优化结果,比网格搜索和随机搜索方法更有效[13];(2)使用数据分解技术与GRU构建分解集成模型。常用的数据分解技术有小波分解、经验模态分解、总体经验模态分解和小波包分解等[14-16]。这些技术可以将具有多种规律特征的原始时间序列分解为一组相对平稳且简单的子序列,从而降低模型的预测难度。其中小波包分解(wavelet packet decomposition,WPD)具有可以人为选择分解层数和分解使用的小波函数等优点,并且能够同时对信号的低频和高频部分进行分解[17-18],进而提升了预测模型的精度。

正确建立分解集成模型是进行径流预测的前提,目前很多研究直接对原始径流时间序列整体使用数据分解技术,这种分解策略会导致分解子序列中每一个时间节点上的数据都包含了来自未来不可获取的数据信息[19-21],从而产生数据泄露问题。所以直接对整个原始径流时间序列使用数据分解技术是不现实的,难以满足实际预测需求。为了解决这一问题,熊怡等[22]设计了一种自适应动态分解策略(self-adaptation decomposition strategy,AS),这种策略是利用观测数据来更新历史样本,在数据分解中避免了引入未来信息,并提升了径流预测的精度。

综上所述,基于目前径流预测中存在的问题,本文首先采用AS策略对原始月径流量时间序列进行WPD分解,称为自适应小波包分解(self-adaptation strategy wavelet packet decomposition,ASWPD)。在不使用未来数据的前提下,充分提取原始月径流量时间序列中的数据特征,以降低预测难度。然后使用BO对GRU进行超参数优化,提出并建立了基于ASWPD-BO-GRU的月径流量预测模型。以黑河流域莺落峡水文站月径流量预测为实例(预见期为1个月)进行模型应用研究,以期为月径流量预测提供一条新思路。

2 数据来源与研究方法

2.1 研究区概况

莺落峡水文站位于甘肃省张掖市甘州区龙渠乡,集水面积为10 009 km2,多年平均径流量为49.225 9 m3/s,径流年内分配十分不均[23]。莺落峡水文站作为黑河上游祁连山出山径流的主控水文站,其径流量的多少直接影响着黑河流域经济社会的发展和生态环境的保护。

2.2 数据来源

本文的月径流量数据来源于国家冰川冻土沙漠科学数据中心 (http://www.ncdc.ac.cn) 提供的黑河流域莺落峡水文站逐月逐年径流资料数据集[24]。从中选取莺落峡水文站1964年1月—2016年12月(共636个月)的月径流量数据作为研究对象,将1964年1月—2006年12月(共516个月)的月径流量数据划分为模型训练集,将2007年1月—2016年12月(共120个月)的月径流量数据划分为模型测试集。

2.3 研究方法

2.3.1 小波包分解(WPD) WPD是在小波分解(wavelet decomposition,WD)的基础上产生并得以发展的,与WD不同的是,WPD在分解信号低频部分的同时,也对高频部分继续分解,并且能够根据信号特征和分析需求,自适应选取对应的频带来匹配信号的频谱,从而具有更广泛的应用价值。WPD算法公式如下[17,25-26]:

(1)

式中:dlj,2n、dlj,2n+1为小波包系数;j为尺度参数,j∈{i,i-1,…,1};l、k为平移参数;n为频率参数,n∈{2j-1,2j-2,…,0};hk-2l、gk-2l分别为小波包分解中的低通、高通滤波器组。

重建算法为:

(2)

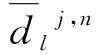
2.3.2 自适应小波包分解(ASWPD) 本文提出的自适应小波包分解(ASWPD)的机理是利用AS策略对原始月径流量时间序列进行WPD分解。其中,AS在分解过程中避免了引入未来信息,只要增加新息,分解进程就会自适应调整。AS的具体操作细节见参考文献[22]。因此,ASWPD能在不引入未来信息的前提下发挥小波包分解提取信号中有效信息的能力。ASWPD的具体分解步骤如图1所示。

图1 自适应小波包分解(ASWPD)的分解步骤示意图

设原始月径流量时间序列为Qt,t=1,2,…,N。

Step 1:对小波包分解算法的分解层数k和母小波函数进行设定;

Step 2:对分解序列的起始长度m进行设定,随着新息的依次添加,待分解序列始终以m+1个长度滚动分解;

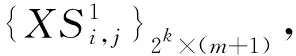
Step 4:经过不断的滚动分解,最终得到2k个子序列,记作{XSi,j}2k×(N-m),用该组子序列进行GRU预测并重构。

2.3.3 贝叶斯优化(BO) BO是一种全局优化算法,适合解决多维、未知的复杂优化问题,能够有效地对神经网络超参数进行寻优处理,从而提高时间序列的预测精度。与随机搜索及网格搜索相比较,BO能更加有效地解决优化问题[13]。BO的具体计算公式和细节见参考文献[27]。另外,本文选用高斯过程和期望改进(EI)函数作为概率代理模型和采集函数。

2.3.4 门控循环单元(GRU) GRU是LSTM的变体,由更新门和重置门两个门结构组成。相比于LSTM,GRU简化了模型结构,训练速度更快,且保持了LSTM的预测效果。GRU的一个单元结构如图2所示。GRU的具体计算公式和细节见参考文献[12]。

图2 门控循环单元(GRU)结构

2.3.5 预测模型构建流程

Step 1:利用ASWPD进行原始月径流量时间序列分解。首先设置WPD的分解层数k和母小波函数以及待分解序列起始长度m,然后对原始月径流量时间序列进行ASWPD分解。得到2k个分解子序列,再将各个分解子序列进行训练期、测试期划分,用于模型建模和测试;

Step 2:数据预处理。为了提升模型的收敛速度,需要对分解子序列数据进行标准化处理。计算公式为:

(3)

式中:xnorm为标准化后的数据;μtr为分解子序列中训练期数据的均值,108m3;σtr为分解子序列中训练期数据的标准差,108m3。

Step 3:确定每个分解子序列GRU模型的输入、输出变量。对各分解子序列训练期数据使用偏自相关函数(partial autocorrelation function,PACF)确定GRU模型的输入变量,输入变量的选取准则为[28]:(1)选择超出置信区间的PACF值对应的滞时变量作为输入;(2)如果存在每个滞时变量对应的PACF值均在置信区间以外的情况,则选择几个滞时小的变量作为输入。当确定了输入变量,若xt-i为输入变量,则xt即为输出变量。

Step 4:利用BO确定各个分解子序列GRU模型的超参数。GRU模型对超参数的选择非常敏感,选择不当会在很大程度上影响GRU的性能,甚至会引起模型过拟合问题;如,GRU隐藏层的层数和每层神经元的数量决定了GRU模型的结构;学习率体现了每次参数更新的幅度大小;L2正则化参数决定了模型的抗过拟合能力;最大训练回合表征模型是否学习充分。因此,设置BO的最大迭代次数,并设置目标函数为训练完成的GRU在训练集上的均方误差,对各个分解子序列的GRU模型采用BO对上述5个超参数进行寻优。利用目标函数构建的优化问题如下:

(4)

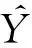
Step 5:对各个分解子序列进行预测并叠加重构得到月径流量预测结果。采用筛选得到的各分解子序列的输入、输出变量和GRU模型超参数分别构建预测模型进行预测,将预测结果反标准化后进行叠加重构得到最终月径流量预测结果。反标准化计算公式为:

xdenorm=xσtr+μtr

(5)

式中:xdenorm为反标准化后的数据,108m3;μtr为分解子序列中训练期数据的均值,108m3;σtr为分解子序列中训练期数据的标准差,108m3。

Step 6:模型评价。选取纳什效率系数(NSE)、平均绝对百分比误差(MAPE)、平均绝对误差(MAE)、均方根误差(RMSE)对模型预测结果进行评价。具体计算公式见文献[29]、[30]。

3 结果与分析

3.1 月径流量序列分解结果

对莺落峡水文站1964年1月—2016年12月的径流量数据采用ASWPD进行分解,根据模型训练期预测结果,设置ASWPD中待分解序列起始长度m为24,分解层数k为2,母小波函数为db4小波基函数,将原始月径流量时间序列分解为M1、M2、M3、M4共4个子序列。分解结果如图3所示。

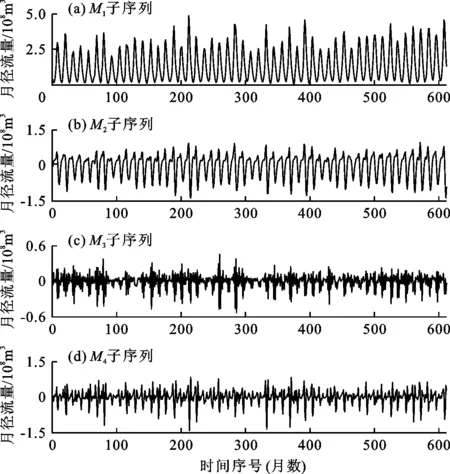
图3 原始月径流量时间序列ASWPD分解图(1964-01—2016-12)

3.2 模型输入变量选择

对分解子序列M1、M2、M3、M4的训练期数据依次使用PACF并遵循上述提到的准则进行GRU模型输入、输出变量的确定。各分解子序列的PACF值如图4所示,最终各分解子序列GRU模型的输入、输出变量选择见表1。

表1 各子序列输入、输出变量

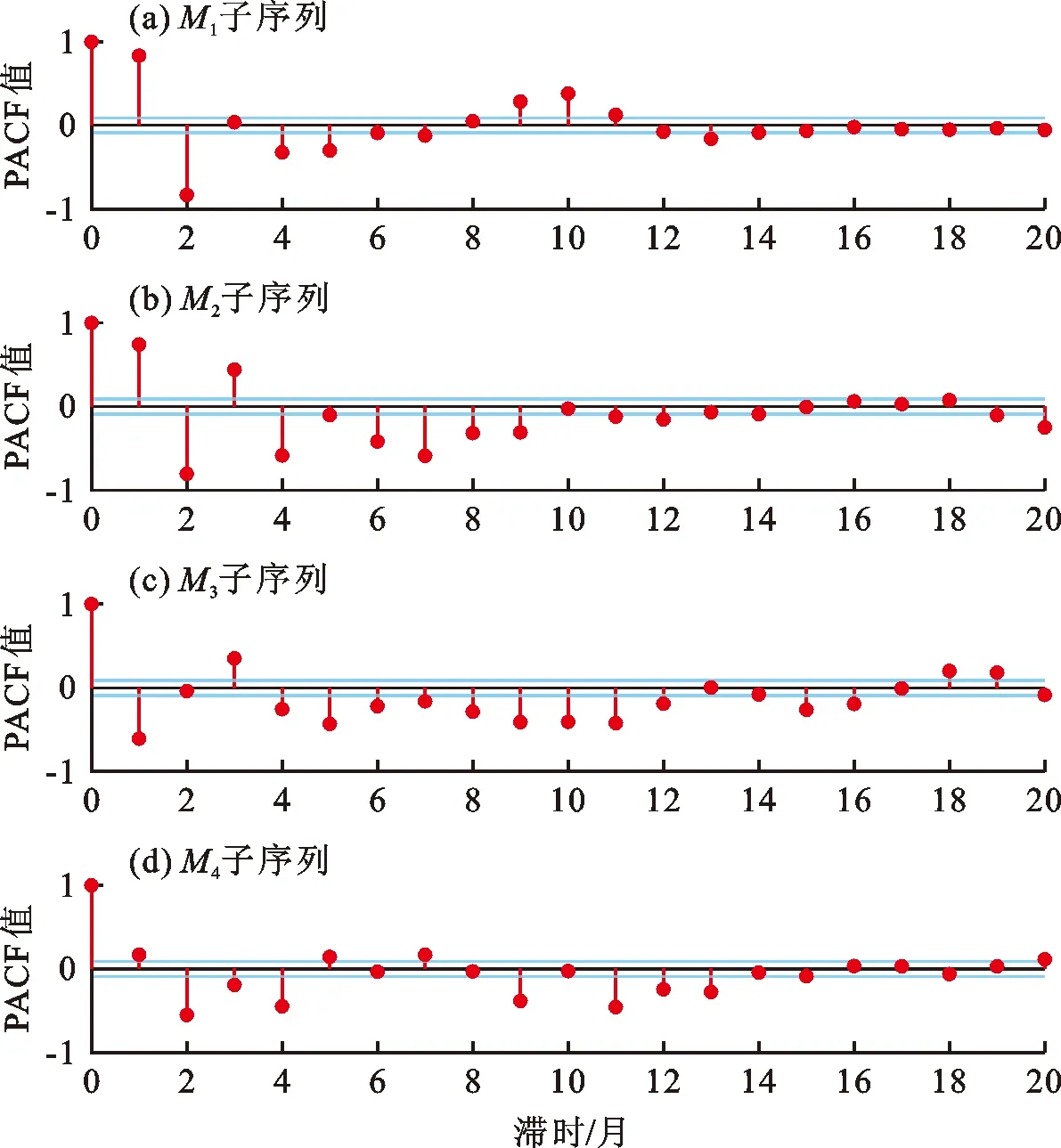
图4 各分解子序列PACF值

3.3 模型参数设置

GRU模型在对各分解子序列的训练过程中,优化器选择Adam算法;设置batchsize为32;设置Dropout为0.5,用于改善模型过拟合问题;设置BO的最大迭代次数为100;设置BO优化GRU模型超参数时隐藏层层数、每层神经元数量、学习率、L2正则化参数、最大训练回合数的寻优范围分别为[1,4]、[1,200]、[10-2,1]、[10-10,10-2]、[1,150],各分解子序列经BO寻优得到的超参数如表2所示。

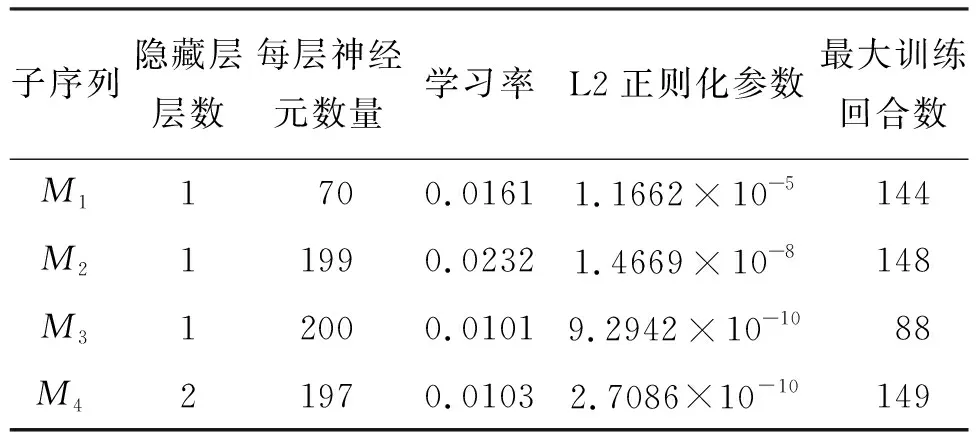
表2 各子序列GRU模型最优超参数

3.4 预测结果及分析

为验证本文提出并建立的ASWPD-BO-GRU模型的预测效果,同时建立了GRU模型、BO-GRU模型、WPD-BO-GRU模型(基于传统分解思想对原始月径流量时间序列整体进行分解的预测模型)共3种对比模型,通过前文2.3.5节选取的4个评价指标对各模型预测结果进行评价。为在相同条件下进行对比验证,对3种对比模型均使用标准化处理数据并用PACF确定模型的输入、输出变量。对GRU模型通过人工经验确定模型的超参数;对BO-GRU模型设置BO算法的最大迭代次数为100,由于ASWPD-BO-GRU模型中BO算法对超参数的寻优范围已足够广泛,所以对BO-GRU模型5个超参数寻优范围的设置与ASWPD-BO-GRU模型相同;对WPD-BO-GRU模型进行3层WPD分解,母小波函数为db4小波基函数,保证原始月径流量时间序列特征能被充分提取,BO参数设置同上。

不同模型在测试期(2007年1月—2016年12月)对莺落峡水文站月径流量的预测结果见图5,各评价指标的计算结果见表3。

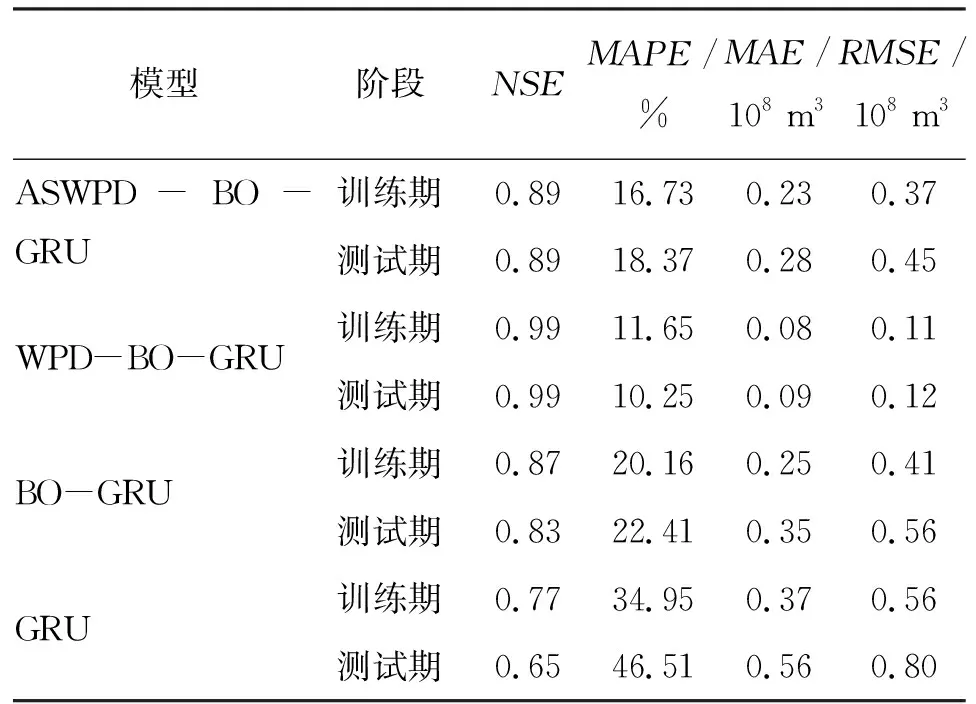
表3 莺落峡水文站月径流量不同预测模型评价指标计算结果

由图5可以看出,在测试期GRU、BO-GRU、ASWPD-BO-GRU、WPD-BO-GRU 4种模型对原始月径流量时间序列的拟合效果依次逐渐提高。其中,单一GRU模型的拟合效果最差,特别在原始月径流量时间序列的峰值和谷值处误差极大,预测效果不佳;BO-GRU模型与原始月径流量时间序列的波动趋势基本接近,相比于单一GRU模型,大幅减小了预测的峰值、谷值误差;ASWPD-BO-GRU模型相比于BO-GRU模型,对原始月径流量时间序列波动趋势的接近程度更好,尤其减少了预测的峰值误差,有效提升了拟合精度;WPD-BO-GRU模型相比于其他3种模型,与原始月径流量时间序列的波动趋势最为接近,预测的峰值、谷值误差也最小,对原始月径流量时间序列的拟合精度最高。

分析表3可以得出:GRU模型测试期的MAPE、MAE、RMSE分别为46.51%、0.56×108m3、0.80×108m3,相比于训练期分别增加了33.08%、51.35%、42.86%,GRU模型测试期的NSE为0.65,相比于训练期减少了15.58%,说明GRU模型出现了一定程度的过拟合问题;BO-GRU模型测试期的MAPE、MAE、RMSE相比于GRU模型分别减少了51.82%、37.50%、30.00%,NSE相比于GRU模型提升了27.69%,与GRU模型相比,BO-GRU模型4个评价指标的训练期与测试期差距也大幅减小;ASWPD-BO-GRU模型测试期的MAPE、MAE、RMSE相比于BO-GRU模型分别减少了18.03%、20.00%、19.64%,NSE相比于BO-GRU模型提升了7.23%;WPD-BO-GRU模型测试期的MAPE、MAE、RMSE相比于ASWPD-BO-GRU模型分别减少了44.2%、67.5%、73.33%,NSE相比于ASWPD-BO-GRU模型提升了11.24%。

上述预测结果与分析表明,BO-GRU模型的预测精度要远高于GRU模型,并且还在一定程度上抑制了单一GRU模型的过拟合问题,提升了泛化能力和预测性能。ASWPD-BO-GRU模型的预测精度要远高于BO-GRU模型,说明ASWPD在数据分解过程中虽然没有使用未来数据信息,但仍能提升模型的预测精度。WPD-BO-GRU模型的预测精度最高,但由于WPD-BO-GRU模型在对原始月径流量时间序列分解时引入了未来数据信息,发生了数据泄露问题,所以才产生了虚高的预测结果,因而无法在实际中应用。而本文提出的ASWPD-BO-GRU模型是在正确分解的基础上建立的,不会发生数据泄露问题,并且NSE接近0.9,说明该模型具有较高的预测精度,相比于其他3个预测模型能更好地应用于实际中。

4 讨 论

本文对莺落峡水文站月径流量的预测结果表明,ASWPD-BO-GRU模型与原始月径流量时间序列的拟合程度较好,在预测精度或实际应用方面优于其他3个对比模型。主要的原因为:

(1)本文利用BO对L2正则化参数进行了寻优,保证了GRU在训练集上的均方根误差尽量小的同时防止了模型复杂度过高,在一定程度上抑制了过拟合问题,提升了模型泛化能力;

(2)GRU模型的最优超参数有时不在人工经验选择超参数的范围之内,因而无法通过人工经验进行最优的超参数选择。应用具有良好的全局搜索能力的BO来优化GRU模型的超参数能在一定程度上打破人工经验选择超参数的局限性,从而更准确地对模型超参数进行选择,BO优秀的寻优能力在其他学者的相关研究中也得到了印证[12,31];

(3)对原始月径流量时间序列整体使用WPD分解技术的传统方法虽然能大幅降低原始月径流量时间序列的非线性和预测难度,提升预测的精度,但该方法在分解过程中使用了未来数据,所以无法在实际中使用。应用ASWPD分解技术能够在不使用未来数据的前提下还能有效地提取原始月径流量时间序列中复杂的有效信息,从而降低预测难度并提升预测精度。因此,本文提出的ASWPD-BO-GRU模型在实际应用中相比于其他3种对比模型的泛化能力更强,具有较高的预测精度和稳定性,能够很大程度弥补单一模型的缺点,并且解决了传统分解集成模型错误使用未来数据的问题,所以可将ASWPD-BO-GRU模型应用于实际月径流量的预测。

此外,由于ASWPD中待分解序列起始长度、分解层数和母小波函数的选择对ASWPD的分解效果影响很大,而本文是通过模型训练期预测结果进行试错确定的,因此可在下一步研究中考虑通过优化算法对上述参数进行寻优以进一步提高分解效果和预测精度。

5 结 论

本文构建了基于ASWPD-BO-GRU的月径流量预测模型,通过对莺落峡水文站月径流量预测的实例分析,得出以下主要结论:

(1)利用BO优化GRU模型的超参数(隐藏层层数、每层神经元数量、学习率、L2正则化参数、最大训练回合数),能在一定程度上打破人工经验选择超参数的局限性和抑制单一GRU模型的过拟合问题,从而能更准确地对模型超参数进行选择并提升模型的泛化能力。

(2)ASWPD能在不使用未来数据的前提下将原始月径流量时间序列分解为相对规律的子序列,可以减弱各种外界因素对月径流量时间序列的影响,降低径流预测的难度。

(3)基于传统分解集成模型思想的WPD-BO-GRU模型会造成“虚假”的高精度预测结果,无法在现实中应用。ASWPD-BO-GRU模型可解决传统分解集成模型错误使用未来数据的问题,并且在实例应用中纳什效率系数(NSE)接近0.9,各项评价指标也优于BO-GRU模型和GRU模型,具有较高的预测精度,说明将ASWPD-BO-GRU模型用于月径流量预测是可行的。