流域变化环境下水文非平稳异方差序列随机建模研究进展

宋松柏

(西北农林科技大学 水利与建筑工程学院, 陕西 杨凌 712100)

1 研究背景

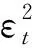
显然,现有条件下水文序列不满足Box-Jekins法ARMA模型建立的前提条件,不能用于这类异方差性波动序列建模,需要研究具有非平稳异方差性序列的建模方法,以扩充现有随机水文学的理论体系。20世纪以来,由ARMA模型发展出了许多新型模型,如外生变量影响干预(auto-regressive moving average with exogenous inputs, ARMAX)模型、周期自回归(periodical auto-regressive, PAR)模型、函数系数(functional auto-regressive moving average, FARMA)模型、波动(auto-regressive conditional heteroskedasticity, ARCH)模型族;SV(stochastic volatility)族、高阶矩模型(generalized auto-regressive conditional heteroskedasticity, GARCH;auto-regressive conditional heteroskedasticity with skewness and kurtosis, GARCHSK)及协整理论( vector error correction, VEC)模型等,旨在改善ARMA模型的性能、预报精度和多角度捕捉描述序列的波动特性,以及描述序列的异方差性、异偏度和异峰度特性的能力,这些模型符合变化环境下异方差性波动水文序列的特性。目前,上述模型在金融、经济等领域取得了许多成功应用案例。但是,这些模型在水文领域的应用起步较晚,且尚未开展对其他新型优良波动性模型的研究[1-12]。基于上述背景,本文在总结国内外水文非平稳异方差建模研究进展的基础上,探讨目前进一步需要研究的主要内容,提出一些主要的研究思路和解决途径,以期为精确描述变化环境下流域水文要素值的变化规律、涉水工程规划设计与科学管理、干旱风险调控提供依据。

2 异方差模型在水文中的应用

2.1 异方差特性

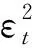
2.2 异方差模型应用实践

Romilly[13](2005年)建立了全球月平均气温长期平均变化季节ARIMA(auto-regressive integrated moving average)模型和残差序列方差随时间波动的GARCH模型。结果表明,ARIMA-GARCH模型提高了ARIMA模型的拟合精度。Chen等[14](2008年)应用ARMA模型和ARCH模型建立了中国台湾省乌溪河10日径流量模型,研究结果表明,与ARMA模型相比,ARCH模型将效率系数从0.28提高到了0.76,平均绝对误差从60.45 m3/s降低到了41.35 m3/s,ARCH模型呈现出良好的性能。Modarres 和 Ouarda也是异方差水文序列建模较多的学者,他们的研究包括:(1)加拿大Alberta省Campsie站月降水的SARIMA-GARCH模型[7];(2)降雨序列ARIMA-GARCH模型和径流序列GARCH模型,通过GARCH模型有效捕捉ARIMA模型残差序列异方差特性[8];(3)加拿大Quebec省Matapedia River流域日径流的ARIMA-GARCH模型[9];(4)伊朗干旱与大气环流指数(southern oscillation index, SOI;north atlantic oscillation, NAO)多变量自回归条件异方差GARCH模型[10];(5)加拿大Bagotville机场站加拿大全球气候模式(CGCM3 T47)输出数据与日最高、最低气温间的多变量自回归MGARCH(multivariate generalized auto-regressive conditional heteroskedasticity)模型[11]。Yusof等[15](2013年)建立了马来西亚半岛(西马)Ipoh和Alorsetar站日降水量ARIMA-GARCH模型。Szolgayov等[16](2017年)构建了斯洛伐克共和国Hron和Morava站KLN洪水模拟模型残差序列GARCH模型。Liu等[17](2017年)建立了非平稳泉流量ARMA-GARCH模型。Fathian等[12](2018年)用Zarrineh Rood Dam流域日降水和径流资料建立了VARX(vector auto-regressive with exogenous input)和VARX-MGARCH模型,结果表明,MGARCH模型的主要型式——对角VECH(diagonal VECH,DVECH)模型能够刻画VARX模型残差的条件协方差和条件相关结构随时间的变化;VARX-DVECH模型能够捕捉降水-径流过程的异方差特性。Farshad[18](2019年)以伊朗西北地区Urmia Lake 流域Zarrineh Rood大坝以上控制区6个水文站日径流量为例,发现径流序列残差平方εt2即方差序列(均值E(εt)=0,Var(εt)=E(εt2)-[E(εt)]2=E(εt2))的自相关函数随时间发生变化,并利用Urmia Lake 1986-2016年的逐月水位序列,建立了径流、气温、降水、风速、相对湿度、日照时数为影响变量的ARIMA-MGARCH多变量水位均值和方差时变模型,指出在这个动态过程中径流具有最长的记忆影响。Khalek等[19](2019年) 利用孟加拉共和国西北部月平均地下水水位数据,开展了GARCH模型和小波-GARCH模型研究,结果表明小波-GARCH模型在刻画波动性和预测方面最优。Liu等[20](2019年)以山东省5个站点的月SPI-9干旱指数建立了ARMA和ARMA-GARCH模型,表明ARMA-GARCH模型在模拟和预测精度方面优于ARMA模型。Pandey等[21](2019年)利用印度Agartala(湿润地区)和Jodhpur(干旱地区)月降水量资料建立了SARIMA-GARCH耦合模型,且取得了良好的运行效果。

在国内,北京师范大学王红瑞教授是国内较早开展水文序列异方差模型研究的学者[3-6,22-23],如:王红瑞等[3-4](2008年)提出了基于异方差检验的水文序列隐含周期模型,并应用于新疆维吾尔自治区塔里木河流域阿拉尔水文站和新渠水文站年天然径流数据的周期分析,结果表明,研究区两站径流序列存在42.7 a的隐含周期,所建立的模型能够较深层次地挖掘分析径流序列周期;王红瑞等[22](2009年)针对水文序列的异方差性,利用河南省淮河流域的鲇鱼山水文站月径流资料,建立了异方差分析模型,取得了较好的应用效果;王红瑞等[23](2012年)以宜昌水文站1949—2001年日径流数据为例,首先提取季节成分,然后,利用剩余成分序列建立ARMA模型,最后,对ARMA模型残差序列建立GARCH模型,结果表明,与ARMA模型相比,在同一置信水平下,GARCH模型能够提高预测置信区间的精度。孙怀卫等[24](2015年)建立了宜昌气象站参考作物腾发量SARMA(seasonal auto-regressive moving averoge)模型,发现参考作物腾发量变化过程存在条件异方差特性,4类GARCH模型验证结果表明,GARCH类模型能够很好地描述参考作物腾发量方差变化特征,其中,EGARCH(exponential GARCH)的性能最佳,可深度挖掘参考作物腾发量的波动规律。王喜华等[25](2011年)利用小波分析原理,首先对降水序列进行分解与重构并进行检验,建立了ARCH、ARMA、ARMA-GARCH模型;其次,进行序列成分叠加,获得基于小波分析的ARMA-GARCH模型;最后,将模型应用于通榆地区年降水量分析,研究结果表明小波分析的ARMA-GARCH模型是一种可行的预测模型。Wang等[26-27](2022、2023年)应用ARMA-GARCH模型进行日径流模拟,取得了满意的模拟效果。除此之外,还有水位-流量曲线估计中的异方差分析(顾西辉等[28](2014年))和大坝安全监测统计模型中的异方差问题(周元春等[29](2002年))等研究。

3 存在的主要科学问题

根据上述国内外研究进展,变化环境下非平稳强波动水文序列异方差建模研究存在以下主要科学问题,迫切需要进一步研究和解决。

(1)差分运算是利用自回归模型来分离提取序列蕴含的线性趋势和曲线趋势的确定性成分,也是将实际中非平稳化序列转换化为平稳序列一种常用的方法,称这种非平稳序列为差分平稳序列。一般来说,线性趋势序列通过一阶差分提取出线性趋势,可消除线性趋势的影响。通过二阶或三阶差分可提取曲线趋势的影响,序列周期(步长)的差分可以消除周期成分的影响。但是,随着差分阶数的增加,差分剩余序列的信息损失也随之增大。因此,非平稳序列过度差分对ARMA模型的建模产生较大影响,导致错误的模型结构,需要进一步研究新的非平稳模型建模方法。

(2)常用的水文序列平稳性统计检验方法(时序图法、自相关系数法、分段检验法和游程检验法)往往具有主观性,而欠缺定量性。ADF(augmented Dickey-Fuller)检验法使DF(Dickey-Fuller)检验推广到了ARMA(p,q)模型平稳检验。但是,ADF检验法包含维纳过程(Wiener process)的积分,在给定显著水平下,相应的临界值也没有解析函数求解,只能通过数值模拟进行计算。许多统计学论著中给定的临界值表格数据有限,有时无法找到给定显著水平下对应的临界值。因此,需要进一步研究不同显著水平下DF检验(无漂移自回归结构、有漂移自回归结构、带趋势回归结构)和ADF单位根检验统计量的临界值,为非平稳水文序列建模提供依据。

(3)与ARMA模型相比,ARCH和GARCH建模较为复杂。现有非平稳异方差序列建模研究基本上以ARMA-GARCH或ARIMA-GARCH模型为主。这些模型中的扰动项正态分布假设偏离了水文序列偏态分布特性。因此,有必要引入扰动项偏态分布(或非正态分布),进行ARCH和GARCH模型的建立,以提高模型对高峰后尾波动特征的刻画能力。

(4)现有ARCH和GARCH模型中采用ht作为εt2的线性函数,水文序列主要采用一元模型(ARCH、GARCH、EGARCH、TARCH)模型、多元模型(VEC、对角VEC),但对于非平稳强波动序列来说,εt2的ht非线性函数能够反映水文序列的强波动特性。因此,近年来发展了GARCH族的许多新型模型。如一元参数GARCH模型(Log-GARCH、IGARCH、MARCH、AARCH、Nonlinear GARCH、GJR、APARCH、C-GARCH、β-GARCH、MS-GARCH、GQARCH、HGARCH、VSGARCH、FIGARCH、N-Component GARCH、FIEGARCH、ANST-GARCH、MEM、HYGARCH、COGARCH、Spline-GARCH、IESTAR-GARCH、分数增广-GARCH);一元非参数GARCH模型、SV模型和多元GARCH模型(BEKK、CCC、DCC)。这些新型模型具有更加灵活的波动弹性,然而却均没有在水文序列分析中得到应用。

(5)波动性模型有GARCH族模型和随机波动SV模型两类。目前,水文序列分析仅开展了GARCH族模型的应用研究,还没有进行SV模型的应用研究。与GARCH族模型相比,SV模型引入了不可观测的隐变量(latent variable),能够灵活和弹性地刻画序列的波动性。因此,有必要开展随机波动SV模型在水文序列建模中的应用研究。

(6)ARCH、GARCH和SV模型描述了低频数据的波动性,而ACD(auto-regressive conditional duration)、EACD(exponential ACD)、GACD(generalized Gamma ACD)等高频数据模型对于序列波动性有较大的影响。由于水利工程、水土保持工程、宏观政策干预等高强度人类活动的影响,这类序列往往与传统非平稳序列的特性差异较大。但是,还未在水文领域中开展这些高频模型的应用研究。

(7)与一元异方差性模型相比,目前关于多元异方差性模型的研究很少,主要开展了向量自回归VAR(vector auto-regressive)模型的应用研究。协整(co-integration)理论是近10年来发展起来的新型多元异方差性模型,如向量误差修正(VEC)模型。这类模型对序列平稳性要求较低,各变量序列间均可为非平稳,只需它们之间的线性组合为平稳序列。因此,协整理论可以解释变量之间的长期稳定的均衡关系,是定量分析非平稳序列之间关系最为重要的工具之一。但是,还未在水文领域中对VEC模型进行应用研究。

4 研究内容与途径

根据上述变化环境下非平稳强波动水文序列异方差建模研究的进展和存在的主要科学问题,本文提出以下主要研究内容和研究途径。

(1)异方差性检验方法。异方差性检验也属于假设检验范畴。如前所述,异方差性是相对于同方差而言的,同方差是指随机误差项为常数,不随时间的变化而变化,如常用的线性回归模型总是假定随机误差项满足同方差性。目前,时间序列分析领域广泛采用的异方差性检验方法有图示检验法(相关图和残差图法)、Goldfeld-Quandt检验法、White检验法、Park检验法和Gleiser检验法。上述这些方法与序列变异点诊断具有类似的结果,即同一具有均值为零的残差序列,其异方差性检验结果相差较大。因此,需要根据平稳性、非平稳性、同方差性、异方差性和协整向量模型特性,应用蒙特卡洛法(Monte Carlo method),通过数值求解获得模拟样本。在此基础上,选取现有的统计检验法,获得异方差性检验结果,评定最佳有效的统计检验法,为后续建模相应特性检验提供检验方法。

(2)扰动项为偏态分布的异方差单变量GARCH模型建模与预测方法。金融学、经济学和信号处理等学科的异方差模型扰动项一般选用正态分布,即对称分布密度函数。这与实际水文序列服从偏态分布的特性不一致。另外,异方差模型参数通用的求解方法是选用极大似然法,对于偏态分布模型来说,获得参数收敛求解仍然是一个复杂的过程。近年来,出现了许多新的参数估计方法。因此,应积极吸取GARCH族模型的最新研究成果,应用条件简化极大似然法、BHHH(Berndt-hall-Hall-Hausman)和GMM(Gaussian mixture modeling)法求解对应模型的参数;应用AIC(Akaike’s information criterion)、BIC(Bayesian information criterion)、quasi AIC(QAIC)、 quasi second-order AIC(QAICc)、Schwarz(SIC)、Shibata、Hannan-Quinn(HQ)、Modified AIC(MAIC)、Modified SIC(MSIC)和Modified Hannan-Quinn (MHQ)法则,开展扰动项为偏态分布非平稳波动单变量GARCH模型的定阶、参数估计和预测方法研究。

(3)单变量随机波动SV模型建模。SV族模型属于随机波动类模型,可采用R、MATLAB和Python软件包以及Eviews等专业软件进行计算。但是,这些计算工具基本上适用于单一特性序列,对于一些复杂的水文序列,需要组合模型描述其特性。另外,近年来SV族模型的一些新型参数估计方法没有包含在上述软件包和专业软件之中。因此,应用采用拟极大似然法(quasi-maximum likelihood,QML)、广义矩法(generalized method of moments,GMM)、有效矩法(efficient method of moment,EMM)和标准矩法(standardised method of moment,SMM),推导相应分布的时变矩估计公式,开展单变量随机波动SV模型的定阶、参数估计和预测方法研究。

(4)多元非平稳强波动模型建模与预测方法。径流受到多种因素影响,多元异方差模型可提高序列的模拟与预测精度。但是,随着解释变量维数的增大,多元异方差模型参数估计的复杂性也大大增加,因此需要研究其稳定和高效的参数估计方法。协整是指对于两个或多个非平稳序列,虽然单个序列不满足平稳性,但选用这些序列的某一组合后,产生的新序列呈现出平稳性。目前,大多数非平稳序列必须经过处理而转换为平稳序列后方可采用常用模型建模。1978年,Engle和Granger提出了著名的协整理论,拓宽了非平稳序列建模的思路和途径。其主要观点是,几个同阶单整序列间可能隐含存在一种长期稳定关系,将其进行线性组合有可能达到降低单整阶数的目的。显然,这种观点符合流域水文变量序列间的变化特性。因此,在上述单变量建模与预测方法的基础上,可应用多元GARCH模型和协整理论模型(VEC)原理,研究符合水文序列特性的多元水文序列新型建模与预测方法。

5 结 论

由于气候变化和高强度人类活动的显著影响,流域水文呈现出高度的复杂特性,破坏了Box-Jekins法ARMA模型建立的前提条件。本文梳理了国内外流域变化环境下水文非平稳异方差序列随机建模的研究进展,提出了目前几个主要研究内容和研究途径,得出以下主要结论:

(1)我国一些流域的水文气象序列存在异方差性,这种异方差性水文序列不能满足Box-Jekins法建立ARMA模型的前提条件。因此,Box-Jekins法不能用于该类异方差性波动序列的建模,需要研究具有非平稳异方差性序列的建模方法。

(2)金融学、经济学和信号处理等领域取得了许多异方差模型成功的应用案例,为流域变化环境下水文非平稳异方差序列随机建模提供了理论基础,在此基础上开展变化环境下水文非平稳异方差序列随机建模是可行的。

(3)分布式水文模型通过流域空间离散单元描述流域下垫面和水循环要素的时空异质性,提高了刻画和反映流域水文过程的真实性。根据现有的研究成果,与集总式水文模型和数据驱动模型相比,分布式水文模型的模拟和预测精度并没有得到显著性提高,而且其建模成本较大,并难以模拟水文序列的异方差性。因此,吸收金融学、经济学和信号处理等领域的最新研究成果,开展异方差序列研究是变化环境下水文序列随机建模的一种实用、可行途径。