基于混合同步控制的构网型逆变器并网系统小扰动稳定性分析

2023-09-11邱晓燕林号缙臧天磊邱一苇周步祥

电力自动化设备 2023年9期

邱晓燕，林号缙，周毅，闫幸，臧天磊，邱一苇，周步祥

（四川大学电气工程学院，四川成都 610065）

0 引言

随着新型电力系统呈现高比例电力电子逆变器、高比例新能源接入的“双高”特性，电网的惯量、阻尼特性呈现下降趋势［1-3］。因此，具有惯量、阻尼支撑特性的构网型（grid-forming，GFM）逆变器受到广泛关注［4］。

目前，常见的GFM 并网逆变器同步控制策略包括功率同步［5］、虚拟振荡器［6］与匹配控制［7］等。其中，技术最为成熟的是功率同步环（power synchronous loop，PSL）控制，其原理是模拟传统同步机的功率传输特性，例如下垂控制、虚拟同步机等。根据GFM 逆变器并网系统直流侧所接直流电源类型的不同，PSL 控制的结构也存在差异。当直流侧为恒功率源（constant power source，CPS）时，功率同步环有功参考值为直流电压控制（direct voltage controller，DVC）的输出信号［8-9］；若直流侧为恒定电压源（constant voltage source，CVS），则有功参考为常数。

针对GFM 逆变器并网系统的小扰动稳定性已开展了大量研究，研究指出由于PSL 与电网阻抗的交互作用，导致GFM 逆变器在强电网条件下易发生小扰动失稳［10］。为了提升GFM 逆变器在强弱电网下的适应能力，有学者提出了基于电网阻抗辨识的跟网型（grid-following，GFL）与GFM 双模式切换控制方法［11］、自适应虚拟阻抗设计方法［12］与包含多变量的H∞控制器［13］；文献［14］提出了一种结合匹配控制理论与非线性角度反馈的混合角度控制，并证明其具有几乎全局稳定的优异性能，但上述控制方法较为复杂。文献［15］直接将锁相环（phase locked loop，PLL）集成到传统PSL 控制策略中，形成了混合同步控制（hybrid-synchronous control，HSC）策略，并通过仿真验证了基于HSC 的并网逆变器在电网短路比（short circuit ratio，SCR）为1或5的情况下具有良好的小扰动和暂态稳定性。

后续研究进一步从理论层面分析了基于HSC的逆变器并网系统的稳定性。文献［16］建立了基于HSC 的逆变器并网系统二阶同步特征方程，指出PLL 支路会增加系统的等效阻尼，从而提升变流器的暂态稳定性。文献［17］基于阻抗模型分析了不同控制参数对系统小扰动振荡模式的局部灵敏度。然而，该研究一方面并未给出不同电网强度下PLL 支路对系统小扰动稳定性的影响规律；另一方面假定直流侧为CVS，仅针对PLL 与PSL 共同作用下的HSC逆变器并网系统进行分析。当逆变器直流侧为CPS 时，HSC 中将包含PLL、PSL 和DVC，由于三者带宽接近，相互作用下对并网系统的小扰动稳定性影响将更加复杂［18］。对于PLL 与DVC 的相互作用，文献［19］和文献［20］进行了相关研究，发现PLL 在弱电网下会产生额外的负阻尼来影响DVC 的稳定性，进而导致并网系统稳定性下降；文献［21］发现DVC和PSL 的相互作用，导致GFM 逆变器并网系统在弱网下的稳定性变差。然而，对于PLL、PSL、DVC相互作用下基于HSC 的逆变器并网系统在不同电网强度下的小扰动稳定性研究尚不充分。

针对上述问题，本文首先建立基于HSC 的GFM逆变器并网系统状态空间模型；其次，在不同电网强度下，分析混合同步环中同步参数对并网系统小扰动稳定性与失稳模式的影响规律；在此基础上，给出混合同步环中附加PLL 支路参数的选取方法，确保基于HSC 的构网型逆变器可在宽范围电网强度下稳定运行；最后，基于MATLAB／Simulink 的仿真模型验证理论分析的正确性。

1 基于HSC的逆变器并网系统结构

基于HSC 的逆变器并网系统如附录A 图A1 所示。电网可通过三相戴维南等效电压源ug和阻抗Zg=Rg+jωLg表示，其中Lg和Rg分别为电网等效电感和等效电阻。此外，电网强度可由SCR 值描述，本文选取5、1 分别代表强和弱电网，假设网侧线路为纯感性，通过改变Lg改变SCR，变化范围为［0.009 8，0.046］H［15］。逆变器输出侧与电网连接，而对于直流侧，本文设置CVS 和CPS 这2 种直流电源。逆变器的硬件电路由开关管S1—S6、LC 滤波器构成。基于HSC 的GFM 逆变器控制策略包含混合同步环、交流电压环、电流环和脉冲宽度调制（pulse width modulation，PWM）模块。其中，混合同步环是该控制策略与其他控制策略的主要不同之处。混合同步环由PLL 和PSL 组成，将公共耦合点（point of common coupling，PCC）q轴电压反馈信号ucoq和功率反馈信号P的输出之和作为逆变器相角信号θ。若直流侧为CVS，则PSL 的功率参考值Pref无需其他环路提供；若直流侧为CPS，则功率参考值Pref由DVC 输出提供。本文中基于HSC 的逆变器并网系统模型的基本参数如附录A表A1所示。

2 基于HSC 的逆变器并网系统小信号分析模型

首先建立基于HSC 的逆变器并网系统的小信号状态空间模型，下文中“Δ”表示模型中相应变量的扰动量。由于同步环节输出相位存在小扰动Δθ，并网系统存在系统dq坐标系与控制dq坐标系，如附录A 图A2 所示。因此，PCC 的电压、电流和调制信号在不同dq坐标系下的统一变换关系为：

图1 混合同步环控制框图Fig.1 Control block diagram of hybridsynchronous loop

忽略基准角频率的扰动量，选择Δθ、Δω1和ΔP作为状态变量，式（2）的线性化结果如式（3）所示。若系统直流侧为CVS，则ΔPref= 0；若直流侧为CPS，则ΔPref由式（5）表示。

式中：udc、Udcref分别为逆变器直流侧电压的实际值、参考值；Kpdvc、Kidvc分别为DVC 的比例系数、积分系数，二者大小由其带宽fdvc确定。选择γdvc作为状态变量，DVC 的状态空间表达式如式（4）所示，该部分的小信号模型如式（5）所示。

同时，DVC 控制下的逆变器直流侧电容动态可被描述为：

式中：Pm为并网系统直流侧的有功功率；Pdc为输入逆变器直流端口的有功功率。Pdc可以用逆变器的输出端口电压uc和电流ic表示，忽略Pm的扰动量，则电容动态的线性化结果如式（7）所示。

电压电流双闭环控制框图如附录A 图A4 所示，电压电流双闭环均采用dq解耦控制，根据式（8）所选取的状态变量描述该控制环，结果如式（9）所示。

式中：Rf、Lf分别为滤波电阻、电感。

最后，假设电流环输出调制信号uref与逆变器输出端口电压uc的扰动量相等。联立式（1）—（12），分别得到并网系统直流端为CVS 和CPS 的13 阶和15阶的基于HSC 的逆变器并网系统小信号模型，如附录A 式（A1）所示，具体状态矩阵A如附录A 式（A2）和式（A3）所示。

3 基于HSC 的GFM 逆变器并网系统小扰动稳定性分析

3.1 电网强度对系统小扰动稳定性的影响规律

基于表A1中的系统基本参数，每改变一次并网系统线路参数，都可以通过状态空间模型求解得到对应的稳态工作点。将求解得到的稳态工作点和控制参数代入小信号模型得到相应的状态矩阵，求解特征根，并通过特征根分析法分析DVC、PSL 与PLL中各控制参数对并网系统小扰动稳定性的影响规律。由于所研究的影响规律与网侧阻抗强相关［22］，因此选定SCR 值为5、1 分别作为强电网、弱电网情况，首先分析电网强度对系统小扰动稳定性的影响规律。当逆变器直流侧为CVS 与CPS 时，电网SCR值由5 变为1 情况下的系统特征根分布情况如图2所示。图中：λ1—λ15为特征根。

图2 电网强度变化下的根轨迹图Fig.2 Root locus diagram under different grid strengths

由图2（a）可以看出，当逆变器直流侧为CVS时，在强电网条件下，λ1和λ2以一对共轭根的形式存在。当电网强度由5 降低到1.2 时，λ1和λ2向左移动，系统稳定性逐渐增强；然而，当电网强度继续降低，λ1和λ2演变为2 个实根，其中λ1向右移动，逐渐靠近虚轴，增加了系统单调失稳风险。由此可以看出，在强电网条件下，该系统存在振荡失稳可能，在弱电网条件下，系统存在单调失稳可能。

由图2（b）可以看出，λ1和λ2的根轨迹与图2（a）所示的变化规律不一致。图2（b）中由于DVC 的加入，引入了2 个新特征根λ14、λ15。在强电网条件下，λ14、λ15以一对共轭根的形式存在，在电网强度减弱至1.2 的过程中，λ14、λ15变成2 个实根，其中λ15向右移动，λ14向左移动。随着弱电网强度进一步减弱，λ14与λ1形成新的共轭根并向右移动，说明系统存在失稳风险。

综上所述，不论逆变器直流侧为CVS 还是CPS，该系统在SCR为1和5时，均有较大的失稳风险。因此，下文将分别以SCR为1和5作为弱电网与强电网的典型场景进行研究，分析PLL 带宽、PSL 比例系数和DVC 带宽对逆变器并网系统小扰动稳定性的影响规律［17］。案例1 —5 的参数设置见附录B 表B1。

3.2 控制结构中不含DVC 时控制参数对并网系统稳定性的影响规律

由3.1节可知，DVC的引入会导致系统的特征根数量改变，因此对控制结构中含有和不含DVC 的情况进行分类讨论。另外，为方便后续对比混合同步环中PLL支路的加入对采用PSL的传统GFM并网逆变器系统的影响，本节在PLL控制参数fpll=0的情况下，分别分析PSL比例系数、DVC 带宽对系统小扰动稳定性的影响规律。

1）PSL比例系数的影响。

当并网系统同步控制策略仅含PSL 时，系统特征根数量减少为12个。根据案例1的具体控制参数设置，绘制随PSL 比例系数变化的系统根轨迹图，如附录B 图B1 所示。由图B1（a）可以看出，在强电网条件下，当KpP由0.000 75 增大到0.003 时特征根λ1、λ2向右移动并进入右半平面，系统将出现振荡失稳。此外，从图B1（b）可以看出，在弱电网条件下，随着KpP由0.000 75 增大到0.003，系统无右半平面特征根，始终稳定。

2）PLL带宽的影响。

根据以上分析结果与案例2 的参数设置，当基于HSC 的逆变器并网系统直流侧为CVS 时，绘制系统在强、弱电网下主导特征根随PLL 比例系数变化的根轨迹，如附录B图B2所示。由图B2（a）可知：在强电网下，当fpll=0时，系统处于10.7 Hz的振荡失稳状态；随着fpll的增大，系统主导共轭根λ1、λ2由右半平面向左移动，并穿越到左半平面，系统转变为稳定状态。然而，从图B2（b）可以看出，在弱电网下，随着fpll的增大，特征根λ1从左半平面向右移动进入右半平面，系统将发生单调失稳。

以上结果表明：当控制结构中不含DVC 时，同步环中PLL 支路的加入会提高GFM 逆变器并网系统在强电网下的小扰动稳定性，但会降低弱电网下系统的稳定性。并且，若附加PLL 支路的控制参数选取不合理，则会分别引发该系统在强电网和弱电网下的振荡失稳和单调失稳。

3.3 控制结构中含DVC 时其控制参数对并网系统稳定性的影响规律

1）DVC带宽的影响。

当并网系统直流侧为CPS 时，同步环中需加入DVC。根据案例4 的参数设置，在强、弱电网下系统主导特征根随DVC 带宽fdvc变化的轨迹如附录B 图B3所示。由图B3（a）可知，强电网条件下，当fdvc由0增大至2 时，主导特征根λ1、λ2移动至右半平面，根据特征根对应的虚部可知，并网系统将发生7.8 Hz的振荡失稳。由图B3（b）可知，在弱电网条件下，当fdvc由0 增大至2 时，主导特征根λ1与λ14移动至右半平面，表明系统将出现1.6 Hz 的振荡失稳。根据以上分析可以看出，无论在强电网还是在弱电网条件下，DVC带宽的增大均不利于并网系统的稳定性。

2）PSL比例系数的影响。

当并网系统同步控制策略含DVC 时，系统特征根数量为14 个。参考案例3 的参数设置，基于HSC的逆变器并网系统主导特征根随PSL 比例系数变化的轨迹如附录B 图B4 所示。在PSL 中，比例系数的影响规律与基于PSL 的逆变器并网系统基本一致，此处不再赘述。

对比3.2 节中对PSL 比例系数的影响的分析结果可知，不论控制结构中是否含有DVC，PSL 比例系数增加均有利于GFM 逆变器并网系统在弱电网下的稳定，但会增加强电网下的失稳风险。

3）PLL带宽的影响。

根据案例5 的参数设置进一步讨论当考虑DVC时，PLL 带宽对系统小扰动稳定性的影响规律。当fpll由0 增加为30 时，系统在强、弱电网下的根轨迹如附录B图B5所示。由图B5（a）可知，在强电网下，随着fpll的增大，主导特征根λ1与λ2由右半平面向左移动，并越过虚轴进入左半平面，表明在该情况下系统由10.6 Hz 振荡失稳演变成稳定状态。由图B5（b）可知，在弱电网下，当fpll由0 增加为30 时，特征根λ1与λ14由左半平面移动至右半平面。并且在取值范围7～22 内，随着fpll的增大，共轭根λ1与λ14向右移动且均位于右半平面，系统处于振荡失稳状态；随着fpll的继续增大，在取值范围22～30内，特征根λ1与λ14由一对共轭根转变为2 个实根，且特征根λ1继续向右移动，系统处于单调失稳状态。

综上所述，混合同步环中附加PLL 支路时，DVC对系统的影响结果与不含DVC 时的情况相似，这里不再赘述。然而，值得注意的是，由于受DVC 的影响，同步环中PLL 的加入会导致该系统在弱电网下存在振荡失稳或单调失稳2种模式。

3.4 HSC控制参数对系统稳定性的影响小结

梳理3.1—3.3节分析结果，小结如表1所示。表中：“↓”、“↑”分别表示系统稳定性降低、提高。

表1 混合同步环控制参数对系统稳定性的影响Table 1 Influence of control parameters of hybridsynchronization loop on system stability

4 小扰动下混合同步环控制参数的可行域分析

由第3章的分析可知，PLL的加入可使并网系统在强、弱电网下稳定运行，但PLL 与PSL 控制参数对基于HSC 的逆变器并网系统的影响规律较为复杂，难以指导混合同步环中附加PLL 带宽的选取。因此，下面对该系统的参数可行域进行分析。

为了方便表述，首先给出失稳参数区域定义：若某一区域内的参数组合无法满足系统在给定电网强度范围（即SCR 值为1～5）内稳定运行的要求，则该区域为失稳参数区域。根据附录A 表A1设置参数，考虑控制中不含DVC 且系统失稳风险最高的情况，采用逐点法分别给出使系统在SCR 值为1 失稳和在SCR 值为5失稳的2类失稳参数区域与其边界，并绘制该系统在小扰动下混合同步环控制参数的可行域如图3所示。从图中可以看出，系统在SCR值为1～5情况下的稳定性受KpP和fpll取值的共同影响。因此，为了使得系统在宽电网强度范围内稳定运行，KpP的变化会影响fpll的选取，当KpP为0.001 时，附加PLL支路的fpll需要在0～12.6 范围内选取；当KpP为0.002时，fpll的取值范围为14.8～17.9。

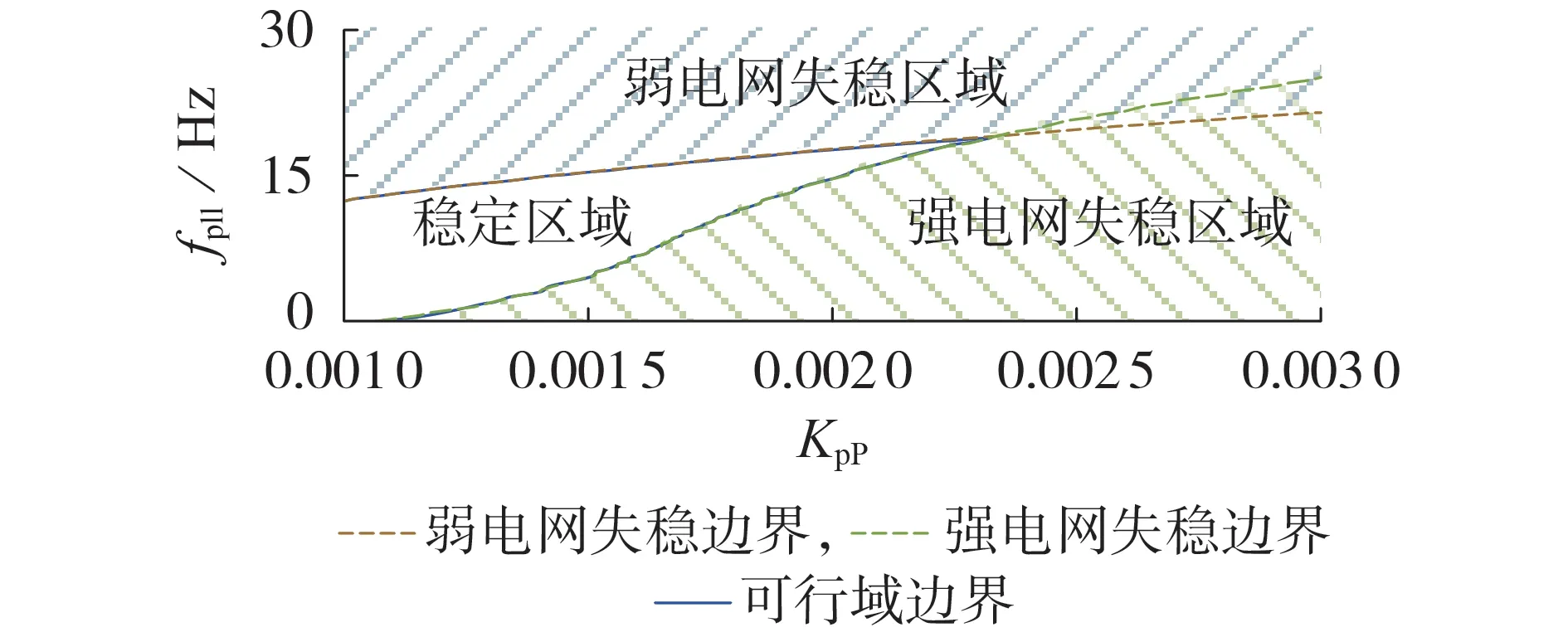
图3 考虑KpP和 fpll的系统控制参数可行域Fig.3 Stability region of system control parameters about KpP and fpll

不同DVC 带宽下的混合同步环控制参数可行域如图4 所示。由图可知，DVC 带宽的增大会增加系统失稳的风险。在KpP=0.001 5 的情况下，若使得系统能够在SCR 值为1～5 范围内稳定，则当fdvc=0时，fpll的取值范围为4.6～15.5；当fdvc=0.4 时，fpll取值范围为8.8～14；当fdvc=0.8 时，fpll无论取何值都无法满足要求。此外，为了使得系统在宽电网强度范围内稳定运行，不同fdvc下，KpP的变化对fpll的选取影响规律与本章对图3的分析结果一致，这里不再赘述。

图4 不同DVC带宽下系统同步环控制参数可行域Fig.4 Stability region of control parameters in synchronization loop under different bandwidths of DVC

综上所述，为了使该系统能够在强、弱电网下稳定运行，对于附加PLL 控制参数的选取需要与PSL比例系数一同考虑。当PLL加入KpP取值较大的PSL中时，fpll应取较大值；当PLL 加入KpP取值较小的PSL中时，fpll应取较小值。此外，fdvc应选择较小值。

5 仿真验证

为验证以上理论分析结果的有效性，按照附录A 图A1 所示的并网系统拓扑结构与附录A 表A1 的基本参数搭建MATLAB／Simulink 时域仿真模型。按照表A1 中的参数设置，对第3 章中的各案例进行仿真，并将仿真结果与理论分析结果进行对比。

5.1 控制结构中不含DVC时的仿真结果

1）PSL比例系数对系统稳定性的影响。

参照案例1，控制结构中不含DVC 与PSL 比例系数变化的情况下，系统在强、弱电网下的仿真波形如附录C图C1所示。由图C1（a）可知，强电网下，当KpP由0.000 75 变为0.001 5 时，系统出现10.6 Hz 的振荡失稳。由图C1（b）可知，弱电网下当KpP由0.001 5变为0.000 75时，系统仍维持稳定状态。

2）PLL带宽对系统稳定性的影响。

参照案例2，PLL带宽变化时，系统在强、弱电网下的仿真波形如图5 所示。由图5（a）可知，强电网下，当fpll由12 变为0 时，系统由稳定状态转变为振荡失稳状态，振荡频率为10.9 Hz。由图5（b）可知，弱电网下，当fpll由12变为25时，系统出现单调振荡失稳现象。

图5 案例2的输出功率波形Fig.5 Simulative waveforms of output power in Case 2

5.2 控制结构中包含DVC时的仿真结果

1）PSL比例系数对系统稳定性的影响。

参照案例3，考虑控制结构中含DVC 与PSL 比例系数变化的情况下，系统在强、弱电网下的仿真波形分别如附录C 图C2 和图C3 所示。由图C2 可知，强电网下，当KpP由0.000 75 变为0.001 5 时，系统由稳定状态转为10.6 Hz 的振荡失稳。由图C3 可知，弱电网下，当KpP由0.001 5 变为0.000 75 时，系统仍保持稳定。

2）DVC带宽对系统稳定性的影响。

参照案例4，DVC 带宽变化时，系统在强、弱电网下的仿真波形分别如附录C 图C4 和图C5 所示。由图C4 可知，强电网下，当fdvc从0.4 Hz 变为2 Hz时，系统出现7.6 Hz 的振荡失稳。由图C5 可知，弱电网下，当fdvc由0.4 Hz 变为2 Hz 时，系统出现频率为1.6 Hz的振荡失稳。

3）PLL带宽对系统稳定性的影响。

参照案例5，混合同步控制中PLL 带宽变化时，系统在强、弱电网下的仿真波形如附录C图C6 —C8所示。由图C6 可知，强电网下，当fpll由12 变为0时，系统由稳定状态转变为10.6 Hz的振荡失稳。由图C7 可知，在弱电网下，当fpll由12 变为15 时，系统出现0.7 Hz 的振荡失稳。然而，当fpll为25 时，弱电网下，系统处于单调失稳状态，如图C8所示。