基于改进型LADRC的STATCOM 抑制双馈风电场次同步振荡策略

2023-09-11刘亚锦廖雨欣刘志坚余成骏段星桅

电力自动化设备 2023年9期

刘亚锦，廖雨欣，刘志坚，余成骏，段星桅

（1.昆明理工大学电力工程学院，云南昆明 650500；2.昆明理工大学现代农业工程学院，云南昆明 650500）

0 引言

风电的装机容量逐年攀升，已成为可再生能源发电的主要组成部分，但我国主要的风能资源集中在中西部地区，与负荷中心整体呈现逆向分布［1］。由于电能输送距离长且规模大，常采用固定或可控串联补偿（以下简称“串补”）来提高线路传输容量［2］。由串补引发的次同步振荡（sub-synchronous oscillation，SSO）事故屡次发生：2009 年，美国德克萨斯州风电场发生了振荡频率为25 Hz 左右的SSO 事故［3］；河北沽源以及吉林通榆的风电场经串补线路送出，分别在2012年和2016年发生振荡频率为6～8 Hz和5.33 Hz的SSO［4］。

工程和实验研究表明，串补与双馈感应发电机（doubly-fed induction generator，DFIG）交互引发SSO 的机理是，DFIG 转子换流器快速控制与串补相互作用，故又被称为次同步控制相互作用（sub-synchronous control interaction，SSCI）［5］。由于风电出力的随机性和时变性，振荡频率也呈现时变的特点，SSCI发散性更强，对电网稳定性的影响也更加恶劣，故亟需开展SSCI特征分析并探索相关的抑制方法。

文献［6-8］分别基于阻抗法、特征值法和复转矩系数法解释了SSCI 发生机理，SSCI 主要影响因素包括串补度、风速、变流器控制参数等。目前SSCI 抑制措施主要分为3 类。①采取切除串补、切机等被动措施来抑制风电场的SSO［9］，但会减少风电场出力，且切除串补会降低线路输送能力和稳定性。②对DFIG 控制器进行优化或附加阻尼控制。文献［10］提出反馈线性化滑模控制替换现有的比例积分（proportional integral，PI）控制器，改善系统鲁棒性，抑制SSO。在DFIG转子侧变流器（rotor side converter，RSC）、网侧变流器（grid side converter，GSC）中附加次同步阻尼控制（sub-synchronous damping control，SSDC）［11-12］。工程实现方面，需要逐台对DFIG进行现场升级改造，工程量大。③利用柔性交流输电系统（flexible AC transmission system，FACTS）装置可实现SSCI 集中抑制。大型风电场会安装FACTS 进行无功补偿，以改善公共耦合点（point of common coupling，PCC）处电压，防止电压跌落对DFIG 转子变流器的损坏，提升系统输电能力。酒泉风电基地装机容量大，主流无功补偿装置在此均有装设，哈密的国华风电场在PCC 处装设了6 套容量为 ± 45 Mvar 的静止同步补偿器（static synchronous compensator，STATCOM）［13］。在FACTS 中附加SSDC来抑制SSCI，不仅可以解决以上方法存在的问题，而且在经济性上具有突出优势［14］。

基于FACTS 附加SSDC 解决SSCI 问题，文献［15-17］分别以DFIG 转子角频率偏差、线路电流以及电压作为输入信号，依靠带通滤波器提取振荡模态分量，经过比例移相环节，向系统注入次同步阻尼电流。振荡频率需要与滤波器中心频率相匹配，比例移相环节参数配置合理，才能获得满意的抑制效果，该类方法无法适应时变的振荡环境。自抗扰控制（active disturbance rejection control，ADRC）不依赖系统精确数学模型，在非线性、强耦合、时变系统中具有较强的鲁棒性。文献［18］在STATCOM 中附加ADRC 阻尼控制器，克服了以滤波器为核心的抑制策略无法适应各种工况的问题，但ADRC为非线性形式，原理复杂且参数众多，工程运用困难。文献［19］提出线性自抗扰控制（linear active disturbance rejection control，LADRC），将控制参数减少到2 个，且控制性能未受影响，在工程中得到广泛应用。

以上研究有以下局限性：①在LADRC 的设计中，通常忽略延时因素，导致观测器输入量之间在时间轴上不匹配，降低控制器的跟踪精度并影响控制的可靠性；②STATCOM 通常采用PI 控制器，但当系统发生SSO 时无法适应非线性、强耦合、时变的环境，同时积分器的计算延时，会造成输出相位偏移；③目前基于LADRC 的阻尼控制仅在原有控制中增加一个LADRC 模块，鲜有文献提出用全LADRC 的控制系统对振荡进行抑制。

针对上述问题，本文提出了基于改进型LADRC的STATCOM 来抑制双馈风电场SSCI。首先，改进了LADRC 以消除延时带来的不良影响。随后，设计了全改进型LADRC 的STATCOM 控制系统，对各控制模块进行建模，进一步得到STATCOM 整体导纳模型，从阻抗角度解释了STATCOM 抑制SSCI 的机理。最后，在时域模型中对比了改进型LADRC、传统LADRC 和PI 控制器对SSCI 的抑制效果，验证了所提方法的有效性。

1 含STATCOM的双馈风电场-串补外送系统

1.1 系统整体结构

本文建立了在PCC 处利用STATCOM 提供电压支撑的双馈风电场经串补线路送出的等效模型，如图1 所示。在系统建模中，假定风电场由N台完全相同的1.5 MW DFIG 并联组成，风电经风电汇集站T1和升压站T2升压后，进入220 kV交流线路，经升压站T3第三次升压后由500 kV 串补线路并入无穷大电网。图中：RL1、LL1分别为220 kV 交流线路的等效电阻和电感；RL2、LL2、CSC分别为500 kV 线路等效电阻、电感和串补电容；up为STATCOM 与系统连接的PCC 电压，STATCOM 并联在双馈风电场的集中PCC处；Δωr为转子角频率偏差量。

图1 含STATCOM的双馈风电场经串补的并网系统Fig.1 Grid-connected system of doubly-fed wind farms with STATCOM through series compensation

1.2 STATCOM数学模型

STATCOM 拓扑结构如图2 所示。图中：Lc和Rc分别为STATCOM 与电网之间的连接电感和电阻；C为直流侧电容值；udc为直流侧电容电压；upa、upb、upc为STATCOM 与系统连接的PCC 处三相电压；ica、icb、icc为STATCOM 注入系统的三相电流；uca、ucb、ucc为STATCOM输出的三相电压。

图2 STATCOM拓扑结构Fig.2 Topology structure of STATCOM

在dq旋转坐标系下，STATCOM 主电路的交流侧和直流侧数学模型可分别表示为：

式中：upd、upq分别为PCC 处电压up的d、q轴分量；ucd、ucq分别为STATCOM 输出电压uc的d、q轴分量；icd、icq分别为STATCOM 向系统注入电流ic的d、q轴分量；ω0为系统额定角频率。

2 基于改进型LADRC 的STATCOM 抑制双馈风电场SSCI控制结构

传统STATCOM可支撑风电场PCC处电压，但不能为系统提供正阻尼并抑制SSCI，故在STATCOM中附加SSDC，为系统提供正阻尼，STATCOM 输出电压不仅包含工频电压，还将叠加次同步分量。STATCOM中电压电流双环控制采用PI 控制器，但PI 控制器中的积分器会产生积分延时，使控制系统整体速动性减弱，并造成输出电压相位偏移，影响抑制效果甚至可能对振荡产生助增作用。次同步信号有非线性、时变的特点，PI 控制器参数适应性差、静态误差较大，无法适应SSCI 环境。文献［20］在三相电压型脉宽调制（pulse width modulation，PWM）整流器中，将全LADRC 系统与全PI 控制系统进行对比分析，全LADRC 系统动态跟踪性能、抗干扰能力和鲁棒性更强。故本文将STATCOM 中电压电流双环控制中的PI 控制器用改进型LADRC 替代，并基于改进型LADRC 为STATCOM 设计附加阻尼控制器，构建改进型LADRC 的控制系统，基于改进型LADRC 的STATCOM控制模型见图3。

图3 基于改进型LADRC的STATCOM控制模型Fig.3 STATCOM control model based on improved LADRC

3 具有延时补偿的LADRC设计

3.1 LADRC传统控制结构

LADRC 结构由跟踪微分器（tracking differentiator，TD）、线性扩张状态观测器（linear extended state observer，LESO）、线性误差反馈（linear state error feedback，LSEF）三部分组成。LESO 输出系统状态变量估计值z1、z2、…、zn和总扰动估计值zn+1，LSEF基于状态误差e1、e2、…、en通过合适的线性组合计算出信号u0。设n阶被控对象如下：

式中：f为总扰动，包括内部扰动和外部扰动；u为LADRC 输出控制量；b0为与受控对象相关的参数；y为被控对象实际输出量。

构造LESO如下：

式中：z=[z1z2…zn zn+1]T为LESO 对状态变量的观测值；β=[β1β2…βn βn+1]T为LESO 增益。当β中元素值配置得当时，观测值将会接近真实值，即z1→y，z2→ẏ，…，zn+1→f，故LESO 可以估计总扰动。通过LSEF环节，最终LADRC的输出控制量u为：

式中：kp、kd、…、kd(n-2)为LSEF 控制增益；v为目标参考值。

LADRC 参数可由极点配置法得到，将LESO 和LSEF 两部分的参数简化为2 个带宽，即LESO 的观测带宽ωg和LSEF 的控制带宽ωc。一阶LADRC 的LESO特征方程λ1(s)和LSEF特征方程γ1(s)分别为：

式中：ωg，1、ωc，1分别为一阶LADRC的LESO观测带宽、LSEF 的控制带宽；β1，1、β2，1为一阶LADRC 的LESO增益；kp，1为一阶LADRC的LSEF控制增益。由式（6）可得一阶LADRC的控制参数为：

类似地，二阶LADRC的控制参数为：

式中：ωg，2、ωc，2分别为二阶LADRC 的LESO 观测带宽、LSEF的控制器带宽；β1，2、β2，2、β3，2为二阶LADRC的LESO 增益；kp，2、kd，2为二阶LADRC 的LSEF 控制增益。

3.2 考虑延时的改进型LADRC

STATCOM 作为被控对象，控制输入信号u到实际输出信号y过程中，存在PWM延时、采样和计算延时等，即y(t+Td)与u(t)之间存在时间误差Td。将Δωr引入STATCOM控制中，由于风电场与STATCOM之间存在一定的电气距离，信号传输延时也需要考虑。LESO的2个输入信号y和u时间轴上的不匹配，将会影响LESO对干扰和系统状态估计的准确性。

考虑延时的改进型LADRC 结构如图4 所示。在信号u输入LESO 之前加入延时模块，使信号y和u在时间上达到同步，提高LADRC 控制器在时滞系统中的控制精度。

图4 考虑延时的改进型LADRC结构Fig.4 Improved LADRC structure considering time delay

联立式（4）、（5）、（7）、（8）可推导出改进型LADRC 输出控制信号u的一阶、二阶LADRC 传递函数分别如式（9）、（10）所示。

4 STATCOM控制器设计

附加阻尼控制器LADRC5采用二阶形式，Δωr从双馈风电场引入STATCOM 过程中需考虑采样延时Ts以及信号传输延时Tc，将延时近似等效为一阶惯性环节，即1/[(Ts+Tc)s+1]，在uer引入LESO 之前加延时环节1/[(Ts+Tc)s+1]，控制器具体表达式见附录A式（A1）。

由式（1）可知，STATCOM 交流侧数学模型为一阶系统，故电流内环控制器LADRC2和LADRC4均采用一阶形式。dq轴电流内环控制器设计原理和参数均相同，以d轴为例，电流内环控制结构见附录A图A1，控制器设计过程见附录A式（A2）、（A3）。

d轴电压外环控制器LADRC1对应电压udc平衡，由式（2）可知STATCOM 直流侧数学模型为一阶系统，故LADRC1采用一阶形式，控制结构见附录A 图A2，具体表达式见附录A 式（A4）、（A5）。类似地，q轴电压外环LADRC3设计过程见附录A式（A6）。

PLL 为同步系统提供跟踪相位θpll，发生SSCI 时PLL 输入电压中含有大量谐波，会使输出相位的误差增大。用一阶LADRC 替换PLL 中原有的PI 控制器（后文简写为“PLL_LADRC”），LADRC 会对谐波量进行估计并补偿，消除系统中的谐波影响，增加同步系统的跟踪精确度，PLL_LADRC 控制原理见附录A 图A3。PLL_LADRC 设计过程见附录A 式（A7）—（A11）。

5 STATCOM的SSCI抑制机理

5.1 STATCOM抑制SSCI阻抗机理

含STATCOM 双馈风电场经串补的并网系统在次同步频率fer下等效阻抗模型如图5 所示。图中：Rr、RRSC分别为风力发电机转子绕组和RSC 的等效电阻；Rs为定子绕组与风电场出口升压变的总电阻；Lr、Ls、Lm分别为转子、定子的漏感以及互感，由于Lm≪Lr、Lm≪Ls，常忽略含Lm的线路；Δur为RSC 在次同步扰动下输出的扰动电压；sr为次同步频率下转子转差率，有sr=(ωer-ωr)/ωer，ωer为次同步角频率，ωr为转子角频率；ZG为DFIG 风电场等效阻抗；ZL为输电网络等效阻抗；Rm、Xm分别为STATCOM 等效电阻和电抗。

图5 含STATCOM的双馈风电场经串补的输电阻抗模型Fig.5 Transmission impedance model of doubly-fed wind farm with STATCOM through series compensation

输电网络中线路与变压器的等效阻抗电路由电阻RL、电感LL及串补电容CSC组成。未加入STATCOM时系统在次同步频率下的等效阻抗Zeq=Req+jXeq可表示为：

式中：RG、XG分别为DFIG 风电场等效电阻和电抗。一般ωer＜ωr，则sr＜0，此时转子呈现负电阻特性，即(Rr+RRSC)/(Nsr)＜0；当转子的负电阻特性使系统整体电阻为负时，Req＜0；此时若系统受到扰动，则由于系统整体呈现负阻尼，将引发持续发散振荡，进而造成严重SSCI事故。

STATCOM 附加SSDC可以增加系统在次同步频率下的正阻抗，如图5 所示，STATCOM 等效为并联可变阻抗Zm=Rm+jXm，投入STATCOM 后系统整体等效电阻R′eq为：

5.2 STATCOM等效建模

由附录A 式（A3）、（A5）、（A6）可得，d、q轴电压外环和电流内环传递函数分别为：

式中：b0，ud、b0，uq和kp，ud、kp，uq和G1，ud(s)、G1，uq(s)以及H1，ud(s)、H1，uq(s)分别为d、q轴电压外环LADRC 的内部控制参数b0，u和控制增益kp，u以及传递函数分量G1，u(s)和H1，u(s)的表达形式；b0，id、b0，iq和kp，id、kp，iq和G1，id(s)、G1，iq(s)以及H1，id(s)、H1，iq(s)分别为d、q轴电流内环LADRC的内部控制参数b0，i、控制增益kp，i、传递函数分量G1，i(s)和H1，i(s)的表达形式。

由式（14）可推导出STATCOM 控制系统的小信号模型，如式（15）所示。

式中：Δup=(upd0Δupd+upq0Δupq)/up0，将其改写为矩阵形式F5，矩阵F1—F5、Fdelay详细表达式如附录A 式（A12）所示，变量下标0 表示对应变量的稳态值，变量前方Δ表示对应变量的小信号分量。

对式（1）、（2）进行拉氏变换，建立小信号模型如下：

6 SSCI抑制效果仿真验证

利用MATLAB／Simulink 搭建了图1 所示的含STATCOM 的双馈风电场经串补线路并网的等值模型，来验证上述SSCI抑制策略的有效性。

6.1 控制参数对STATCOM等效阻抗的影响规律

STATCOM等效为次同步频率下电阻值为正的阻抗，并联在双馈风电场PCC处，将系统整体阻抗抬升至正值。STATCOM 等效阻抗与控制参数密切相关，依据上述推导得到全改进型LADRC 下的STATCOM小信号导纳矩阵，进一步研究参数对STATCOM 等效阻抗的影响规律。增大或减小附加阻尼控制器、电压外环和电流内环LADRC 参数，参数变化对STATCOM 等效阻抗的影响规律见附录B 图B1。由图可知：附加阻尼控制器参数的变化对阻抗的影响最为显著，电压外环控制参数对阻抗影响不大；电流内环控制器LADRC 中控制带宽对阻抗的影响大于观测带宽。

6.2 全改进型LADRC 与部分使用LADRC、全PI 控制器的STATCOM系统等效阻抗对比

基于全改进型LADRC、全PI 控制器、部分使用改进型LADRC（附加阻尼控制+改进型LADRC、电压电流双环控制+改进型LADRC）抑制策略，等效阻抗频率特性曲线对比如图6所示。

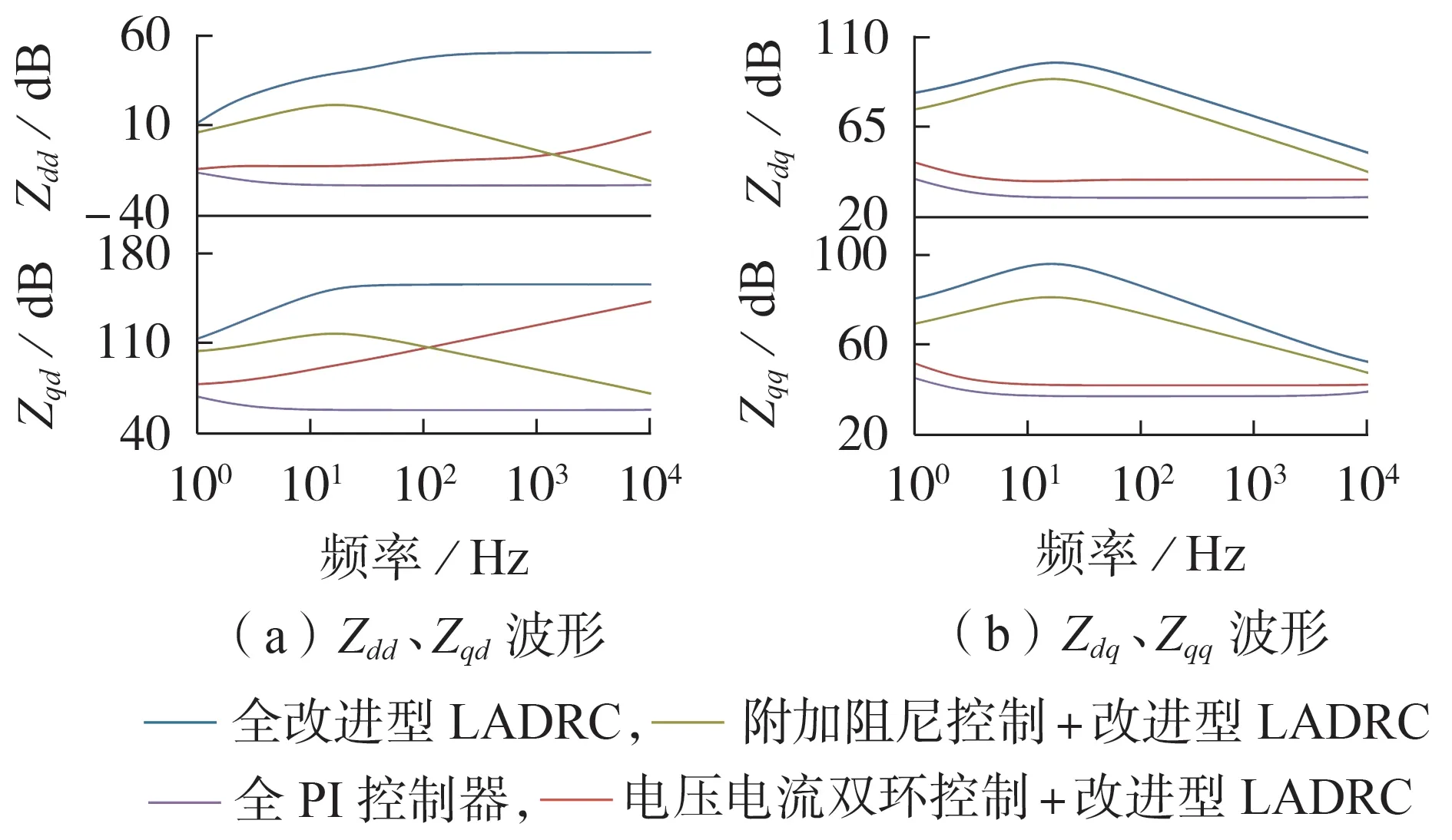
图6 不同抑制策略等效阻抗对比Fig.6 Comparison of equivalent impedance among different suppression strategies

由图6 可知：相较于其他抑制策略，采用基于全改进型LADRC 的抑制策略时阻抗分量幅值Zdd、Zdq、Zqd、Zqq均较高；2种部分使用改进型LADRC 的抑制策略虽然在一定程度上可以增大STATCOM 等效阻抗，但是幅值增量没有全改进型LADRC 抑制策略明显。因此全改进型LADRC 系统的稳定裕度和鲁棒性更强。

6.3 抑制策略效果验证

分别对比基于PI控制器、传统LADRC以及改进型LADRC 的SSCI抑制策略的抑制效果。DFIG 处于额定运行状态，风速为额定风速15 m／s，在6 s时投入串补电容，3 种抑制策略下DFIG 输出响应的仿真结果如图7、8所示。

图7 不同抑制策略DFIG输出有功、无功响应曲线Fig.7 Output active and reactive power response curves of DFIG under different suppression strategies

由图7 可知，当输电线路的串补度突变为40 %时，DFIG输出有功功率P、无功功率Q波形将会在此扰动下发生持续振荡且振荡没有衰减，波形中出现大量次同步分量。基于PI控制器、传统LADRC和改进型LADRC 抑制策略均可以使次同步分量逐渐衰减。但在改进型LADRC 抑制策略作用下，相比传统LADRC 和PI 控制器，DFIG 输出有功功率和无功功率振荡幅度更小，收敛速度更快。由图8 可知，采用改进型LADRC 抑制策略后，定子电流总谐波畸变率（total harmonic distortion，THD）由PI 控制下的1.17 % 和传统LADRC 下的0.62 %，下降到0.39 %。由此表明，基于改进型LADRC 的抑制策略可以有效抑制系统SSCI，相较于PI 控制和传统LADRC，动态追踪速度更快，有更强的暂态和稳态响应能力。

图8 不同抑制策略下定子电流THDFig.8 THD of stator current under different suppression strategies

6.4 鲁棒性测试

6.4.1 串补度变化

系统在稳定运行状态下，6 s 时在线路中投放串补度为40 %、60 % 和80 % 的串补电容，保持控制器参数不变，得到在不同串补度下基于改进型LADRC、传统LADRC、PI控制器的抑制策略对SSCI抑制能力的对比结果，如图9所示。

图9 不同串补度下DFIG输出有功功率响应曲线Fig.9 Output active power response curves of DFIG under different series compensation

由图9 可知：串补度越大，系统的振荡幅度也越大，抑制策略对振荡的抑制速度也会有一定程度的减慢；各抑制策略在不同串补度下，使DFIG 输出功率振荡逐渐趋于收敛，但在PI 控制器下，DFIG 输出功率在9.5 s 仍存在小幅度振荡，且随着串补度的增加振荡抑制效果也减弱。在保持参数不变的条件下，PI控制器在一段时间内使DFIG输出的有功功率降低，且串补度越大，功率降低越明显。传统LADRC在不同串补度下使振荡逐渐趋于收敛且不会影响DFIG 的输出功率，但在振荡逐渐收敛进入稳态的一段时间内，DFIG 输出的有功功率仍存在微小振荡，在振荡收敛快速性和扰动估计精准度方面都逊色于改进型LADRC。在实际工程中，我国高压输电串补度集中在35 %～45 %，基本不能达到80 %。因此改进型LADRC 可以在参数不变的条件下对不同串补度引发的SSCI进行有效抑制。

6.4.2 风速变化

由于风电场出力具有随机性和时变性，在不同风速下考虑基于改进型LADRC、PI 控制器的抑制策略对DFIG 的SSCI 抑制效果。分别选取风速为15、12、9 m／s，使DFIG 稳定运行一段时间，在6 s 投入补偿度为40 % 的串补电容，对比分析2 种抑制策略在不同风速下的SSCI抑制效果，如附录B图B2所示。由图可知：在不同风速下，未投入抑制措施时，双馈风电场经串补输电系统会发生持续性的振荡；改进型LADRC 不改变控制参数，可以在不同风速下为系统提供正阻尼，DFIG 输出有功功率振荡都可以在大约0.5 s 内快速收敛并趋于稳定；基于PI 控制器的抑制策略不改变控制参数，风速越低则抑制效果越弱，当风速为9 m／s时抑制策略失效，不能使振荡收敛。