弱电网下直驱风机网侧换流器建模及稳定运行控制策略分析

2023-09-11蔡寿国卫志农

电力自动化设备 2023年9期

朱瑛，何飞，蔡寿国，卫志农

（河海大学能源与电气学院，江苏南京 211100）

0 引言

随着“双碳”目标的不断推进，大量新能源并入电网，风电作为新能源发电的重要形式，其稳定运行至关重要。而风电场一般远离用电负荷中心，通过远距离输电并入电网，并网系统呈弱电网特性，将造成风机的电气及控制系统失稳［1-3］。

国内外针对直驱风机并入弱电网引起的失稳问题的研究方法主要包括频域阻抗建模法［4］和基于稳态点线性化的特征值分析法［5］2 种。其中特征值分析法基于状态方程建立系统的全阶小信号模型，通过状态矩阵的特征值获取系统的稳定信息，但此方法需要建立详细的系统模型且计算量较大，应用于大规模的风电场还会面临“维数灾”的问题［6］。因此，相较于特征值分析法，频域阻抗建模法具有更加明确的物理意义，得到了更加广泛的应用。

频域阻抗建模法又可分为正负序阻抗建模法和dq轴阻抗建模法2 种。文献［7-8］采用正负序阻抗建模法得到一维的阻抗模型，但由于锁相环（phase locked loop，PLL）、控制参数等引起的不对称，正负序阻抗会存在耦合，影响稳定性判断结果的精确度［9］。文献［10］通过建立系统dq轴阻抗模型，考虑非对角元素的影响，应用广义Nyquist 判据研究电网强弱及PLL 动态对于系统稳定性的影响，分析结果更加精确。

但是，通过二维dq轴阻抗矩阵判断系统的稳定性，需要采用频域矩阵的特征值轨迹法，这种方法不仅很难确定稳定裕度，而且不能量化系统参数对稳定性的影响。文献［11］通过坐标变换将二维阻抗模型转变为一维阻抗模型，这种方法计算量大且变换复杂；相比于二维的阻抗建模法，单输入单输出（single-input single-output，SISO）模型可以量化系统的稳定裕度，稳定判据更加简洁。文献［12］通过dq轴阻抗建模推导的方式建立SISO 模型，对直驱风机与电网交互引起的失稳问题展开了详细的机理分析，对各控制参数的影响进行了评估，给出了增强稳定性的各控制参数调整方法，但是没有量化传递函数表达式。文献［13］研究了各控制参数对于系统稳定性的影响，但没有对系统的控制结构及参数做出进一步的改进。因此有必要对直驱风机网侧换流器（grid-side converter，GSC）与弱电网交互系统进行阻抗建模，探究dq轴阻抗建模的嵌套方法，简化稳定判据，量化系统的稳定裕度，并探讨参数多目标优化方法。

然而，在dq轴阻抗建模过程中，由于PLL 的存在会使得dq轴之间的耦合程度加深，在小扰动情况下会造成相角偏差，导致电气系统与控制系统参考坐标系的错位，出现振荡失稳问题［14］。弱电网特性越明显，PLL、电网及GSC 的耦合程度越深，系统越容易失稳［15-16］。针对PLL 引起的上述问题，学者们提出了一系列改进方法，包括相角补偿［17］、PLL 参数优化［18］、自适应控制［19］等。但是这些方法只关注了PLL 自身的带宽和阻尼比，参数设计方法较为单一，且自适应控制需要根据电网阻抗变化实时调整控制参数，对于硬件设备具有很高的要求［20］。综上所述，采用外部的控制设备及附加算法在一定程度上改善了系统的稳定性，但对设备的实时测量和控制性能以及算法的稳定性提出了更高的要求。相比之下，进行控制系统结构改进及参数优化更具有实际可行性。

针对GSC 与弱电网交互系统的稳定性问题，相较于二维dq轴阻抗模型，本文以风机并网点电压为接口变量建立交互系统的传递函数模型；以电流参考指令的扰动量作为输入，将dq轴进行嵌套，建立可以量化描述交互系统稳定性的SISO 传递函数模型。基于SISO 模型研究以下内容：①弱电网对于交互系统稳定性的影响；②考虑PLL 影响的交互系统稳定性；③弱电网下PLL 结构改进与参数多目标优化设计。结果表明，SISO 传递函数模型可以准确描述交互系统的稳定性，所提的3 阶PLL 结构与参数设计方案能够更好地适应弱电网下的运行工况，提高系统的稳定裕度，保证SISO 交互系统在宽范围下的稳定运行。

1 直驱风机并网互联系统数学建模

1.1 直驱风电系统拓扑结构

直驱风机接入弱电网模型见图1，由风力机、永磁同步发电机（permanent magnet synchronous generator，PMSG）、机侧换流器（rotor-side converter，RSC）、GSC 组成。图中：Lf为滤波电感；Lg为网侧电感；C为直流电容。

图1 直驱风机接入电网模型Fig.1 Model of direct-drive PMSG connected to power grid

直驱风机与弱电网交互系统是一个电气系统与控制系统交互的多时间尺度的动态模型，因此有必要对模型进行一定的简化，在保证系统准确性的前提下，聚焦于系统稳定性的关键环节。本文对弱电网下直驱风机的动态模型进行如下几点简化。

1）以直驱风机为研究对象，当直驱风机运行于稳态工作点时，由于RSC、GSC 之间直流电容的作用，使直驱风机的机网侧相互解耦，因此可将风力机、PMSG、RSC 等效为受控电流源，通过调节直流电流模拟直驱风机的输出功率变化。

2）本文主要关注的是电流内环与PLL 的动态交互，即交流电流时间尺度下系统的稳定性，而直流电压环与功率外环的带宽远低于所研究的振荡频率范围，对小信号输入反应迟缓，因此本文忽略外环对阻抗模型的影响，将直流侧电压简化为定值；另一方面，PLL 不同于电压外环，是直接作用于受控量达成系统控制目标的最小控制环节。因此，在交流电流时间尺度下，需要考虑PLL与电流环的动态交互［7，21］。

从参数设计角度看，直流电压时间尺度下主要关注外环控制参数设计，通常将电流内环简化为1；在交流电流时间尺度下，通常忽略电压外环，主要聚焦于内环参数设计。经过上述简化，GSC 控制系统主要包括内、外控制环以及PLL 3个部分，控制框图见附录A 图A1。在交流电流时间尺度下，本文简化后的模型与逆变器并网设备具有相同的控制结构，因此本文所提的建模方法和PLL 参数优化方法仍然适用［3］。

本文将短路比（short circuit ratio，SCR）作为评估指标，以评估电网的强弱程度［6］。SCR 为电网短路容量与直驱风机额定容量的比值，其表达式如式（1）所示。

式中：VSCR为SCR 的数值；Ug为电网电压有效值；f为电网额定频率；SN为风机额定容量。

1.2 PLL线性化模型

直驱风机GSC 所采用的PLL通常情况下在传统的静止坐标系下进行建模，结构如附录A 图A2 所示。控制环节采用比例积分（proportional integral，PI）控制，PLL传递函数GPLL表达式如式（2）所示。

式中：kppll、kipll分别为PLL 的PI 控制环节的比例系数和积分系数。

GSC 与PLL 分别基于不同的dq坐标系，两者之前存在一定的误差，为建立GSC 与弱电网交互系统的SISO 闭环传递函数模型，需要分析电气系统与控制系统坐标系之间的转换关系，将两者统一到相同的坐标系下。设dq表示电气系统坐标系，dcqc表示控制系统坐标系，αβ表示两相静止坐标系，3组坐标系的关系如图2 所示。图中：θpcc为并网电压在dq坐标系的相角；θPLL为PLL 输出相角；Δθ为θpcc与θPLL之间的相角差；upccd、upccq分别为并网电压的d、q轴分量。

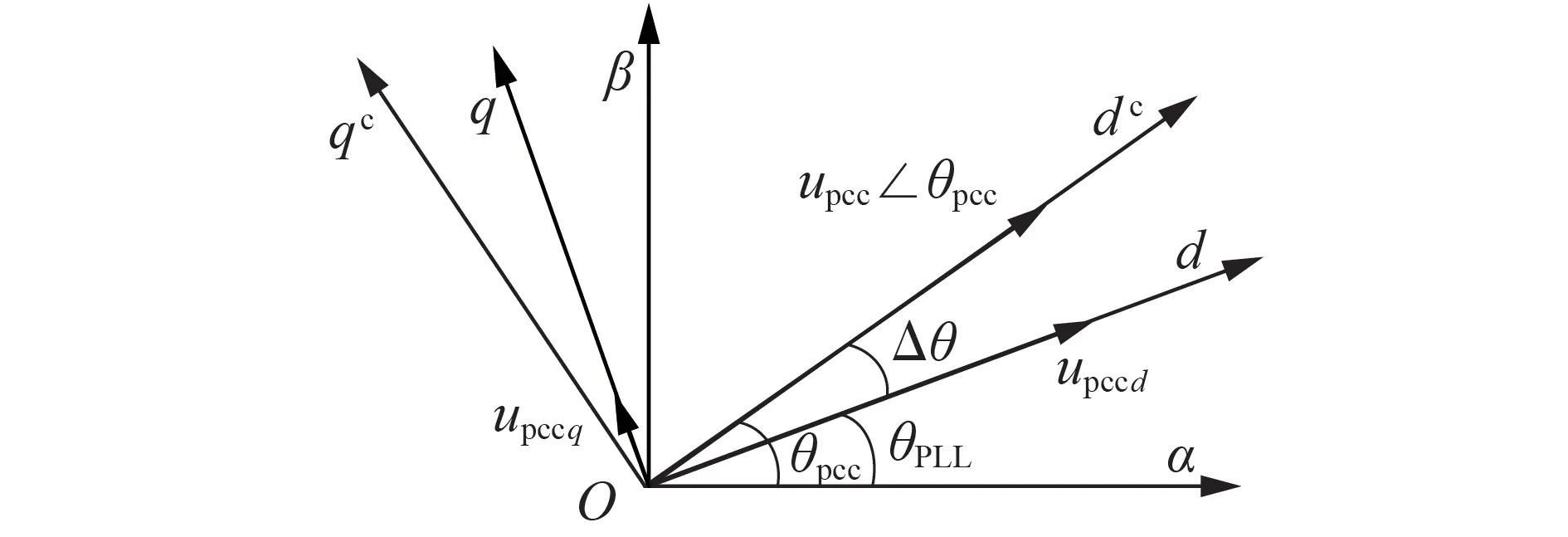
图2 电气系统与控制系统坐标系关系Fig.2 Coordinate system relationship between electrical system and control system

在稳定运行情况下，PLL 能够精确跟踪并网点电压，此时Δθ=0°，upccq=0，2 个坐标系下的电气量数值相同；由于PLL输出相角的小扰动，电气系统和控制系统坐标系下的dq分量关系如式（3）所示。

式中：下标0 表示各变量的稳态值；Δ 表示各变量的扰动量，后同。忽略高阶项，对式（5）进行化简可得考虑PLL 动态后不同坐标系下扰动量之间的关系，如式（6）所示。

1.3 GSC模型

由附录A 图A1 所示控制系统结构框图可知，当输入扰动量时，dcqc坐标系下的输出参考电压扰动量如式（10）所示。

式中：kp1、kp2和ki1、ki2分别为电流环dq轴控制环节的比例参数和积分参数；ω0为电网角频率；ΔIdref、ΔIqref分别为电流环d、q轴参考值扰动量。

同时，GSC 并网点电压及并网电流也因为PLL的相角扰动误差，导致控制系统物理量与交流网络对应物理量的差异，两者关系如式（12）、（13）所示。

1.4 交流系统模型

在电气系统dq坐标系下，滤波电感及弱交流系统的扰动方程为：

值得注意的是，交流系统稳态运行时，网侧电感的存在使得并网点的电压不仅与电网电压有关，还与并网电流和阻抗的乘积有关。并网电流和电网阻抗对于PLL的输入而言是扰动量，建模各部分电压、电流的稳态量关系如附录A 图A3 所示。上述各部分数学方程构成了直驱风机GSC与弱电网交互系统的数学模型。弱电网环境下，将GSC 与弱电网等效为一个级联系统，即建立考虑PLL 影响的GSC 与弱电网交互系统的数学模型，联立式（2）、（8）—（15）构成的交互系统数学模型如附录A图A4所示。

2 考虑PLL影响的SISO模型

下面主要讨论GSC 与弱电网动态交互的SISO传递函数模型以及PLL 对于交互系统稳定性的影响。首先，对交互系统的传递函数进行耦合化简，建立弱电网下的SISO 模型；然后通过开环传递函数的伯德图讨论PLL 及其控制参数对系统稳定性的影响。

2.1 交互系统SISO模型

在上述建立的GSC与弱电网交互系统的传递函数框图的基础上，考虑交互系统稳态运行时，PLL 精确跟踪并网点电压，且GSC以单位功率因数并网，可以得到upccq0=0、iq0=0，则在图A4 中PLL 只对q轴产生影响。由图A4 可知：dq轴之间存在动态交叉耦合，当ΔIdref=0 时可以将d轴的控制环节嵌入q轴闭环中，从而推导出系统的SISO 模型，具体推导过程如下所述。

对各控制环节施加小扰动，考虑电流内环的解耦控制，则传递函数可以化简为附录A 图A5所示结构。图中传递函数A(s)、B(s)、C(s)、D(s)、E(s)的具体表达式如附录A 式（A1）—（A5）所示。在不考虑PLL 影响的情况下，A(s)和B(s)、C(s)和D(s)具有相同的表达式结构，因此PLL 的影响主要体现在E(s)上。

考虑ΔIdref=0，将d轴的电流闭环动态嵌入q轴中，进一步化简闭环传递函数框图，得到q轴闭环传递函数，如图3（a）所示。进一步变化为图3（b）所示的交互系统SISO模型，d轴的电流环作为q轴电流环的一个内部闭环，该模型以电流环q轴指令变化量为输入，以q轴实际输出电流小扰动量为输出，可以反映整个交互系统的稳定性。图中M（s）的表达式如式（16）所示。

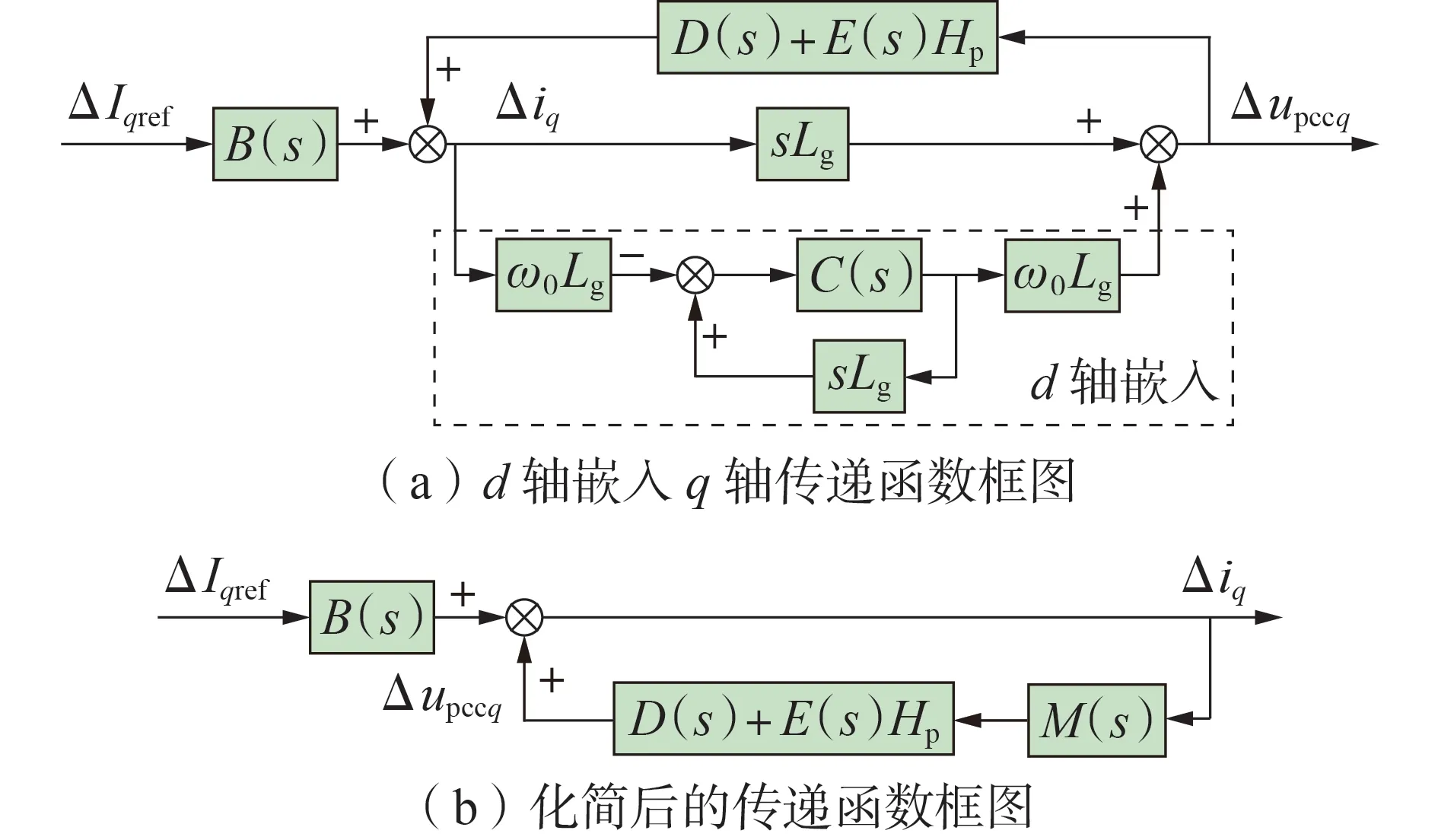
图3 交互系统SISO模型Fig.3 SISO model of interactive system

在设计GSC控制参数时一般没有考虑电网侧阻抗的影响，因此在并入理想电网时系统保持稳定，即B(s)没有右半平面极点。因此对闭环传递函数而言，若H(s)的Nyquist 曲线不包含点（-1，0），则交互系统能保持稳定运行。值得注意的是，在直流电压时间尺度下，增加了直流电压外环，电流内环通常被简化为1，采用本文所提建模方法通过dq轴嵌套的方式，仍然可以将二维阻抗模型化简为SISO模型。

2.2 PLL对交互系统稳定性的影响

通过闭环传递函数可以发现，PLL主要影响q轴的控制结构，进而影响系统的稳定性。在SISO 模型中，体现在闭环传递函数分母中的Hp。

图4 给出了VSCR变化时是否考虑PLL 影响的开环传递函数的Nyquist 曲线。从图4 中可以发现：当不考虑PLL 动态性能时，系统在VSCR变化范围内一直保持稳定；当考虑PLL 动态性能时，当VSCR=3.5时，开环传递函数的Nyquist 曲线包含点（-1，0），系统不稳定。因此，PLL 与交互系统的耦合分析是必要的，其动态响应过程对于系统的稳定性具有重要影响，也表明VSCR越小，系统越容易失稳。

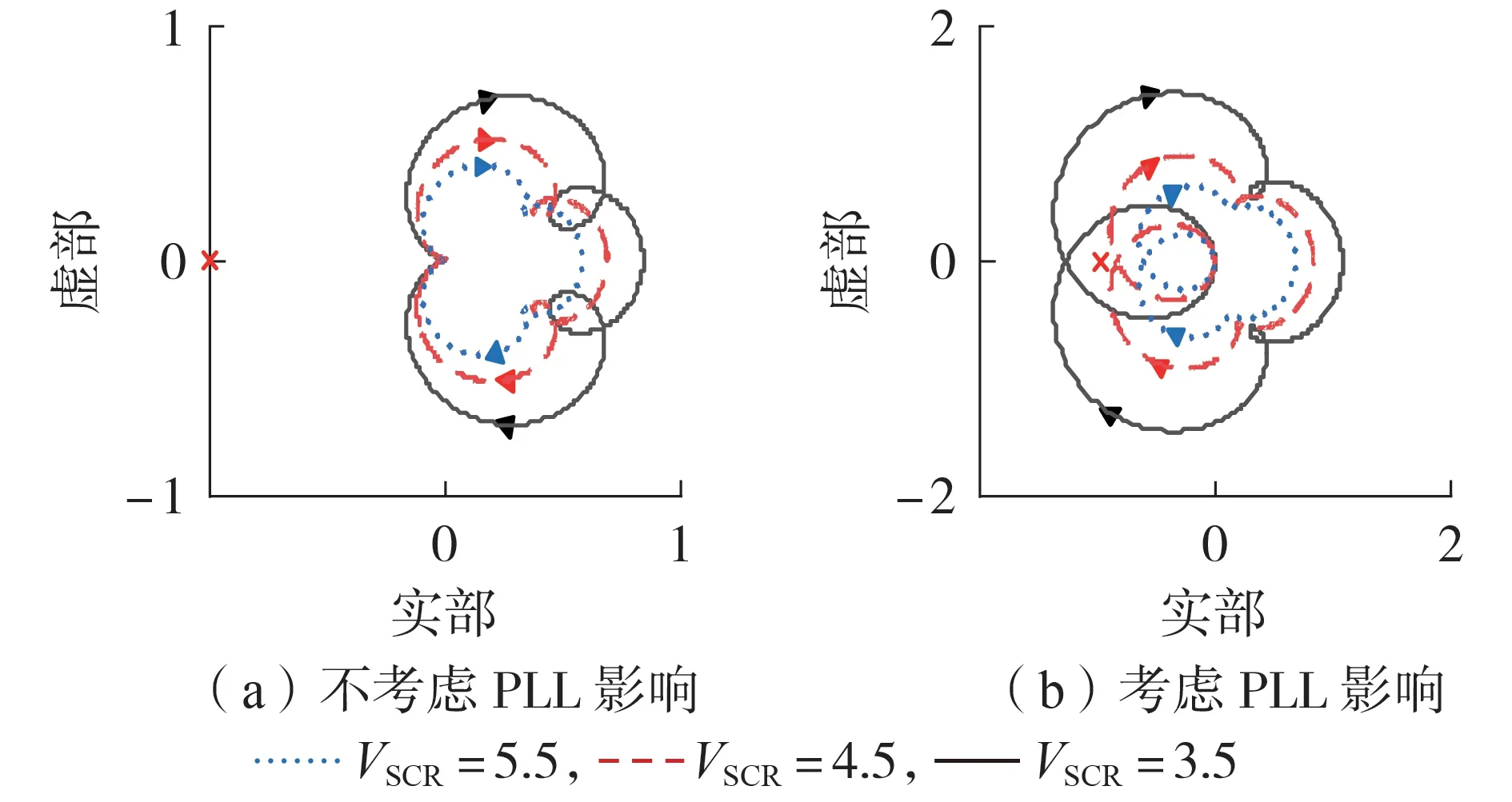
图4 是否考虑PLL影响的开环传递函数Nyquist曲线Fig.4 Nyquist curves of open-loop transfer function with or without PLL influence

由式（18）可知：PLL对交互系统的影响主要体现在(utd0+id0H2(s))Hp，其幅值越小，对于开环传递函数的幅值影响越小；(utd0+id0H2(s))Hp越接近±180°，则PLL对于交互系统的影响越小。因此有必要优化PLL 设计，减小其中低频段的幅值，弱化对交互系统稳定性的影响。

传统PLL 中，PLL 的动态性能主要取决于比例参数，而积分参数主要用于消除跟踪误差。GSC 参数见表1，为分析PLL 参数对系统稳定性的影响，固定积分参数不变，kipll=28，比例参数变化范围为［0.1，0.4］，得到交互系统开环传递函数的Nyquist曲线，如附录B 图B1（a）所示，比例参数变化范围很小，但系统随着比例参数的较小的增幅，很快陷入不稳定状态。另一方面，固定比例参数为0.31，积分参数变化范围为［20，32］，从附录B 图B1（b）所示的Nyquist曲线可以发现，虽然kipll在宽范围内变化，但系统的稳定性没有受到影响。综上所述，交互系统的稳定性主要取决于PLL的比例参数，即相较于积分参数，交互系统对于比例参数的灵敏度更高，同时作出参数变化时PLL 的伯德图，如附录B 图B2 所示，比例参数对于PLL 的幅频特性影响更大，同样验证了上述结论。因此，在交互系统参数设计过程中，有必要考虑PLL性能的约束条件。

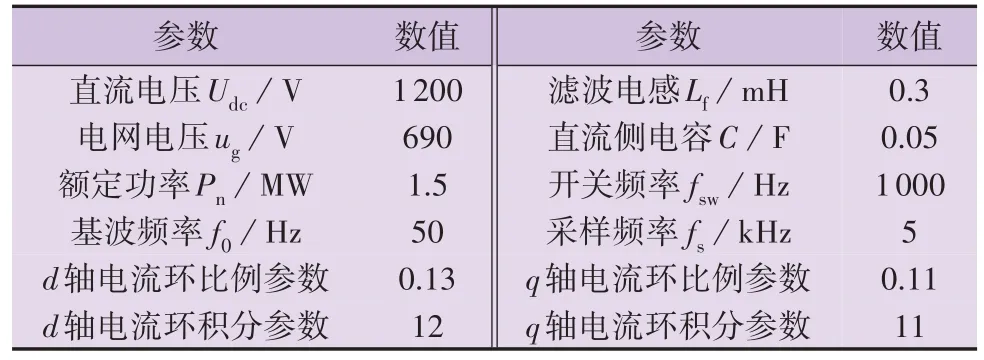
表1 GSC参数Table 1 Parameters of GSC

3 弱电网下PLL改进与参数设计

3.1 3阶PLL参数设计

PLL 对于交互系统稳定性的影响主要体现在Δθ，在对PLL 进行改进时，主要体现在附录A 图A4中的GPLL的不同，因此3 阶建模过程与2 阶一致，只需修改式（18）中的Hp。为了便于PLL的参数设计和性能比较，将传递函数转化为标准形式，量化其性能指标。由前文的推导可知传统PLL传递函数为：

改进的PLL 控制结构如图5 所示。图中：ωp为一阶滤波环节转折角频率；ωref为电网额定角频率；ω为锁相环输出角频率。根据前文推导，弱电网下PLL 的动态交互容易导致系统失稳，为了应对弱电网下由PLL 引起的失稳问题，通常采用2 阶滤波器衰减谐波［7］，增强系统的抗干扰能力，PLL 高频段需要有更大的负斜率。现有的改进方法通过前置滤波器来提高系统的抗干扰能力，但是采用前置滤波会造成基频相角偏差，需要加入额外的相角补偿环节，同时降低带宽可以在一定程度上增强PLL在高频段的谐波衰减能力，但也会降低PLL 的动态性能。因此本文首先考虑在PLL内部，即在upccq部分加入1阶滤波环节，如图5（a）所示，这样不会造成基频偏差，且同样能达到滤波的效果；对于极弱电网下网侧电感造成的输入谐波具有抑制作用，起到了增强稳定性的效果。更进一步，实际上加入1 阶滤波环节就是使传递函数幅值特性具有更好的衰减效果。因此，为了避免传递函数零点对系统稳定性的影响，减少控制参数的个数，便于控制参数的设计，本文合并了1 阶滤波环节和PI 控制，用图5（b）所示2 阶控制系统代替（图中k1—k3为2阶控制系统的控制参数），同样可以在高频段具有更好的谐波衰减效果，同时可以参考最小节拍响应系统进行参数设计。3 阶相比2 阶对于硬件具有更高的要求，但是，相较于相关研究采用PLL 自适应的控制参数设计方法［19-20］，本文认为3阶PLL的经济性是更优的。

图5 改进的PLL控制结构Fig.5 Improved PLL control structure

新型PLL传递函数Hpn表达式如式（22）所示。

3 阶动态PLL 与传统PI 控制的PLL 的伯德图见附录B 图B3，在低频段，两者具有相同的衰减能力；在高频段，3 阶PLL 对谐波的抑制效果更好，因此具有更优的弱电网适应性。

为了兼顾系统PLL 的动态性能与系统的稳定性，3阶PLL的动态性能相关参数参照最小节拍响应系统取值。最小节拍响应系统是指以最小的超调量快速达到并保持稳态响应允许波动范围内的时间响应，当输入为阶跃信号时，允许波动范围为稳态值的±2 %，且稳态误差为0。3阶标准化传递函数GB为：

式中：a、b为3 阶PLL 标准化传递函数的系数。附录B 表B1给出了3阶最小节拍系统的标准化传递函数及响应性能指标，表中的时间均为标准化时间。为了保证系统的动态性能，保持超调量在较小的范围内，3阶PLL标准化传递函数的系数按最小节拍响应系统取值，即a=1.9，b=2.2，本文中ωn的设计需要兼顾系统的上升时间、调节时间与稳定性。图6给出了ωn变化时3 阶PLL 的伯德图，随着ωn的增大，PLL 在高频段的衰减能力变差，系统有可能趋向于不稳定。

同时，ωn的不同取值也影响系统的动态性能，附录B 图B4 给出了ωn增大时3 阶PLL 的单位阶跃响应曲线，随着ωn的增大，系统的动态性能更优，超调量保持在2 % 范围内，调节时间、上升时间减小，系统更快地过渡到稳定状态。

为了兼顾PLL 的动态性能及弱电网下交互系统的稳定性，本文的ωn按照如下原则取值：在系统稳定基础上，PLL的动态性能保持最优，则ωn的取值不宜过小；通过引入3 阶动态PLL，保证系统在弱电网下的稳定性，而直驱风机的输出功率越大，则系统越容易失稳，因此拟在系统运行于额定工况下，保证VSCR=3 系统稳定运行。在额定运行工况下，ωn变化时，系统稳定性判别结果如附录B 图B5 所示，综合以上2 点原则，本文取ωn=110 Hz，兼顾了稳定性与系统响应指标。

3.2 多目标参数优化

在3 阶PLL 参数确定的基础上，已经能够保证PLL 的响应速度，本文区别于传统的单一参数设计，在PLL 参数优化的基础上，对电流环PI 控制参数进一步优化，拓宽系统的稳定域，提高交互系统对弱电网的适应性。于是，首先选定3 阶PLL 的控制参数（ωn=110 Hz），探究电流环控制参数对交互系统稳定性的影响。

由式（9）所示系统开环传递函数探究电流内环控制比例、积分参数对稳定性的影响，分别如附录B 图B6、B7 所示。由图B6 可知，随着kp1的增大，Nyquist 曲线逐渐远离点（-1，0），系统稳定裕度增大；由图B7 可知，随着ki1的增大，Nyquist 曲线先靠近点（-1，0），后又远离点（-1，0），表明系统稳定裕度先减小后增大。但总体而言，相较于比例参数，系统的稳定性对积分参数的灵敏度较低；同时，积分参数过小对系统消除静态误差不利，过大会使超调量加剧，甚至引起振荡。同理，q轴电流环控制参数对交互系统的稳定裕度也是同d轴相似的影响规律。

因此，在优化控制参数设计时，选择参数的原则是尽可能增大电流环的比例系数，而对积分系数的选择应该折中，使得交互系统具有尽可能大的稳定裕度。但是值得注意的是，电流环的比例参数也不能很大，前文主要考虑PLL 影响下的稳定性，在PLL参数设计时，也要考虑系统的静态模型传递函数，此时不考虑PLL 影响，系统开环传递函数GT如式（26）所示。

参数优化时，要保证式（26）所示的静态模型传递函数具有足够的幅值裕度和相角裕度，本文将幅值裕度设置为［2，5］dB，相角裕度设置为［30°，45°］，根据以上设计原则，在VSCR=3 的条件下优化参数，尽可能增大交互系统的稳定运行区间。因此，参数选择的原则是，在折中积分参数的基础上，尽可能增大比例参数，同时保证静态模型的幅值裕度和相角裕度。在上述原则的基础上，由图B7 及式（26），本文取ki1=12、ki2=11，在积分参数确定情况下，取kp1=0.3、kp2=0.3。

4 仿真验证

4.1 SISO模型有效性验证

为了验证本文所推导的SISO 模型的有效性，在MATLAB／Simulink 中搭建图1 所示的GSC 与弱电网交互系统模型，电气及控制系统参数见表1。在采用传统PLL 的条件下，PLL 比例参数为0.312 5，积分参数为28。为验证开环传递函数Nyquist 稳定判据的正确性，改变电网侧电感，使VSCR从5.5变至3.5。

VSCR变化过程中a 相并网电流的波形见附录C图C1。由图可知：VSCR为5.5或4.5时，并网电流波形经过短暂的振荡之后迅速恢复到稳定状态；而VSCR=3.5时，并网电流出现畸变，振荡之后呈发散状态，系统失稳。仿真波形验证了SISO 模型的正确性，同时也表明，随着电网阻抗的逐渐增大，即VSCR的减小，PLL 与GSC 及电网的交互程度加深，交互系统越容易失稳。

4.2 3阶PLL稳定性验证

为说明本文所提的3 阶PLL 相较于传统PLL 的优越性，在3 阶PLL 的ωn=110 Hz 的情况下，按照式（11）的标准化传递函数取值，使两者在低频段具有相同的幅值特性，主要区别在于3 阶动态PLL 在高频段具有更好的谐波衰减效果。在仿真模型中，通过调整VSCR，观察系统的稳定性，验证本文所提结构的优越性。

3 阶PLL 在不同VSCR情况下的并网电流波形见附录C图C2，新型PLL在系统运行于额定工况下，且VSCR=3.5时仍然可以保持稳定运行；而传统PLL的电流波形已经发生畸变，波形呈发散状，交互系统失稳，表明本文所提的3 阶PLL 具有更好的弱电网适应能力。进一步降低VSCR得到附录C 图C3，可以发现，VSCR=3 时新型PLL 仍然可以过渡到额定状态，保证系统的稳定运行。

为验证上述多目标参数优化的有效性以及电流环参数优化后的宽范围运行特性，与上述3 阶PLL的电流波形进行对比。图7 给出了VSCR变化时采用多目标优化设计后的a 相并网电流ia波形，同附录C图C3 相比，当VSCR进一步降低时，优化后的控制参数系统能够更好地适应电网的宽范围变化，在极弱电网下仍然可以保证稳定运行，但过渡到稳态的时间也相应变长。在VSCR进一步降低的情况下，电网侧电感形成的电压降落作为PLL的扰动输入进一步增大，PLL 完成锁相的任务更加艰难，而本文3 阶PLL 的ωn的取值兼顾了动态响应性能和稳定性，在极弱电网下，系统的扰动增大，必然会带来系统过渡到稳态的时间变长。而本文的主要目标是保证极弱电网下交互系统的稳定运行，因此系统的动态性能可以做出一定的让步。