生成对抗网络的无监督高光谱解混
2023-09-09靳淇文马泳樊凡黄珺李皞梅晓光
靳淇文,马泳,2,樊凡,2,黄珺,2,李皞,梅晓光,2
1.武汉大学 电子信息学院,武汉 430072;
2.武汉大学 宇航科学与技术研究院,武汉 430079;
3.武汉轻工大学 数学与计算机科学学院,武汉 430023
1 引言
由于高光谱成像仪自身空间分辨率的不足、大气混合效应、地物种类的复杂多样性等原因,使得每个像元可能同时包含了多个基本地物的光谱信息。该像元被称为混合像元(童庆禧 等,2016;韩竹 等,2020;Jin 等,2019a)。大量混合像元的存在给高光谱图像像元级的精确解译、亚像元级的弱小目标探测与识别带来了很大的困难(Bioucas-Dias 等,2012;Jin 等,2019b;Ma 等,2019,2021;Mei 等,2018)。因此解混对于提升高光谱遥感应用的精度、拓展其应用的广度和深度的具有关键性的意义。
线性光谱解混模型(LMM)以其简单高效、物理意义明确等优点是目前解混领域中研究的重点。LMM 假设的是高光谱图像中每个像素点是由若干个端元的谱线与其各自的丰度系数线性组合而成。其中基于几何以及统计的模型是传统解混的两大主流方法。基于几何的方法是将图像中的像元投影到若干子空间中,并将单形体的顶点看做为图像端元。顶点分量分析VCA(Vertex Component Analysis),N-FINDR 即为属于这一类的代表方法。这类方法简便快捷,但是需要光谱数据满足纯端元的假设。对于空间分辨率相对较低的高光谱数据,该类纯端元假设可能不成立。基于统计的解混模型框架不需满足图像中的纯端元假设,因此也为传统方法的另一大主流模型。例如基于统计的贝叶斯方法可以通过利用统计假设和施加先验约束构造端元和丰度的最大后验概率同时实现端元的提取和丰度的反演的功能。作为传统框架的主流方法,在解混的本质上是一个种迭代的优化问题,因此所面临的主要挑战来自于混合像元数量、噪声以及异常值的鲁棒性的问题。这些因素都在很大程度上影响着模型收敛方向是否接近最优解以及收敛速度的快慢(Jin等,2021)。
近年来,随着深度学习的发展,基于神经网络的解混框架逐渐在高光谱解混中受到了广泛的关注。例如,Palsson 等(2021)提出的基于空间光谱相似性的卷积神经网络框架CNNAEU 以及Borsoi等(2020)所提出的基于变分编码器VAE的生成网络框架。受益为网络训练本身优秀的学习能力以及泛化性能,这些方法都较传统的解混方法在精度上有了很大的提升。近期基于深度学习中自编码器(AE)的方法在无监督的高光谱解混任务中逐渐成为了热点问题,由于该网络框架的训练过程可以简单地描述为通过最小化重构误差来学习图像的低维表示(即丰度系数),并用其对应的权重(端元)进行组合来减少重构误差。因此十分适合运用于非监督的解混任务中,以同时获得高光谱图像的端元和丰度。然而,这些基于学习的方法的一个显著缺点是训练过程更接近于一个黑盒机制,这导致该类方法很难像传统学习的方法一样将端元及丰度的先验知识融入进网络框架中进行训练。这样的缺点也往往导致网络的泛化和精度严重依赖于训练样本的数量和质量。对于现有的基于自动编码器的方法,网络的先验知识往往只是在满足丰度的物理意义(ANC 和ASC)的前提下,通过基于端到端重建误差准则去找到网络误差最小的解。由于高光谱数据本身训练样本数量的限制,网络鲁棒性较差而且往往会产生异常且无意义的解混结果,模型也大多会出现过拟合现象。为了解决上述问题,现有的一些方法DAEN(Su 等,2019),uDAS(Ying,2019)均采用基于纯像素端元提取算法VCA 来直接初始化网络解码器的权值,即将提取得到的端元先验知识并入网络进行训练。然而,由于端元提取的不稳定性,网络对于噪声和初始条件的设置将极大地影响其解混性能。而生成性对抗网络(GANs)在一定程度上可以看作是一种增强模型(Goodfellow 等,2014)。与传统的非对抗模型相比,判决器相当于提供了一个自适应不同任务和数据集的损失项,可以有效提升网络对异常值和噪声的鲁棒性。
因此,本文将在传统自动编码器的基础上,设计了一种全新的对抗自编码器(AAENet),通过在判决器中加入丰度的先验知识,将生成器的隐藏层(丰度)与初始化的丰度进行对抗训练而进一步提高整个网络解混性能。同时也避免了采用网络权重中直接进行端元初始化带来的次优化问题。
2 AAENet网络框架
基于传统自编码器网络框架图如图1 所示。Y∈RN×B代表输入的高光谱图像(N表示像元的数量,B表示图像的维度),代表由解码器重建的高光谱图像。根据LMM 模型假设可知,光谱的混合方式可以描述为:Y=AM+Nnoise。这里Nnoise代表高斯噪声,A表示为图像的丰度,M表示为端元矩阵。因此对应图1的自编码器模型,我们可知编码器隐藏层的输出A即为图像的预估丰度,所求端元矩阵即为网络中解码器的权重矩阵。本文所设计的基于对抗自编码器网络AAENet 框架流程图如图2 所示。其中图2 中LeakyReLU,Linear,ReLU均代表网络框架中所使用的激活函数。
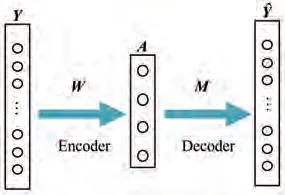
图1 基于自编码器的网络框架图Fig.1 Architecture of the autoencoder-based network

图2 AAENet网络框架图Fig.2 Architecture of the proposed AAENet
2.1 AAENet自编码器网络架构
AAENet 框架中编码器各神经元具体细节如表1 所示。其中R表示为图像中端元的维度数。由上表可以看出前1—4 层神经元主要用于高光谱图像的降维(维度数由9R至R),其转换形式可由以下函数表示:
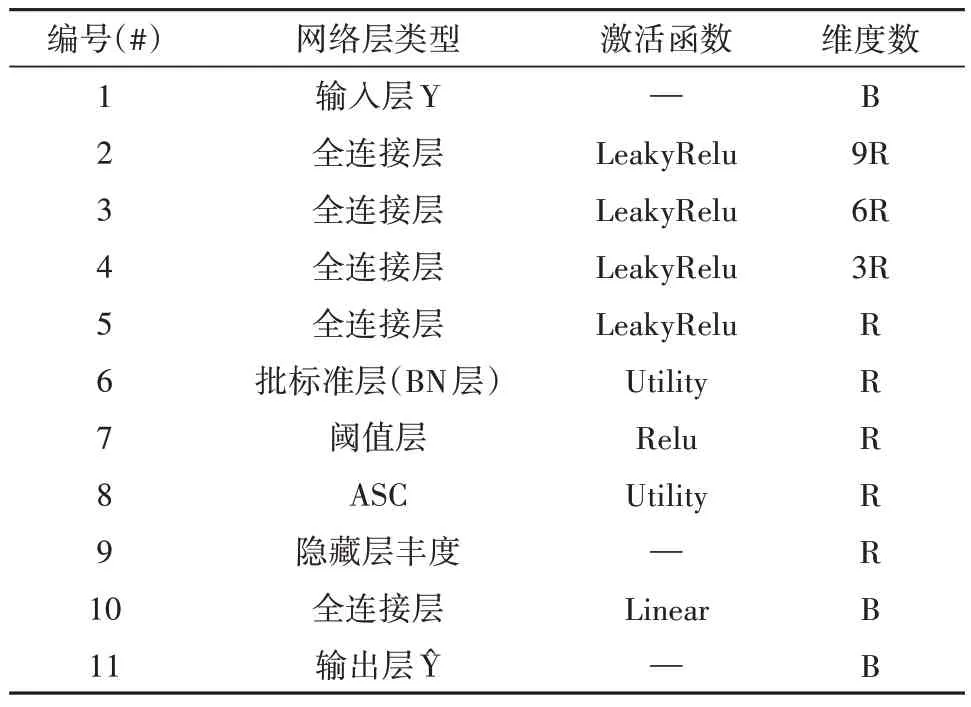
表1 生成器网络层架构及激活函数Table 1 The layer type and activation function used in the generator
式中,a(l)表示为隐藏层的输出,a(l-1)表示为前一隐藏层的输入,W(l)即为该层的权重矩阵。第5 层神经元表示为批标准化层(BN 层),主要为解决网络训练收敛速度过慢或“梯度爆炸”等问题且由γ及β两个参数控制,这里文本假设1,…,m)为前一层神经元的输入,则BN 层的功能函数可以表述为以下形式:
式中,γ,β为网络中的可学习参数,如式(3)所示:
第6层神经元为动态阈值层,考虑到丰度图像的稀疏性,这里本文使用动态阈值α置于每一层的末端单元处作为可学习参数来实现丰度的稀疏性约束。其功能函数可以表示为以下形式:
式中,α(6)表示前一层神经元输入,α为R×1 向量。后续实验表明,采用一个可学习的网络参数α作为动态阈值来控制丰度图的稀疏性限制比在目标函数中加入l1及l21正则项具有更高的解混精度。
由于LeakyReLU 函数本身具有的非负特性,为保证隐藏层所输出丰度的具有物理意义,我们只需在编码器的第7层神经元输出加入一个ASC限制,其功能函数可以表示为因此AAENet 的隐含层中所得到的输入将会自动满足丰度和为一的物理意义。
对于解码器部分,由于本文主要考虑高光谱的线性组合模型(LMM),即观测到的光谱应为端元和其各自的丰度系数线性组合。因此本文使用Linear 作为解码器的激活函数以满足LMM 模型框架的假设。而由于偏置单元在网络的训练中往往会产生很大负值导致收敛性的问题,在本文的网络中所有的偏置单元均置为初始0值。
2.2 AAENet判决器网络架构及损失函数
生成对抗网络(GANs)的概念是由Goodfellow等人提出(Goodfellow 等,2014)。GANs 的训练过程可以看作为寻找判决器D与生成器G两个网络层之间的极小极大的博弈最优点。判决器D 的训练误差为判定输入样本的真伪损失,生成器G 的训练误差则为生成足够逼真的样本欺骗判决器。整个网络的训练损失可以描述为以下形式:
式中,pdata(x)为判决器中接收的真实样本数据,输入x则为从真实的数据分布pdata(x)中获取,p(z)则为生成器所对应生成的样本数据。
如图1 中所示,AAENet 网络中生成器G 由自编码器的编码器层构成,编码器层的输出(隐含层A)即为生成器中产生的样本。判决器D 由3 个全连接的网络层构成,其目的是被训练用来最大限度区分样本是来自隐含层A 的生成样本或是包含丰度先验信息的VCA-FCLS(Heinz 和Chein-IChang,2001)初始化真实样本,而生成器G 则需生成相似的样本最大限度地欺骗判决器。假设K为网络训练的批量大小,则生成器G 以高光谱图像中采样的K个样本y(ii∈ 1,…,K)作为输入,其输出结果需要尽量模仿并生成与初始化丰度图相似的样本数据。两个网络在相互对抗中不断调整参数,最终使得网络可以充分学习丰度的先验知识并生成包含物理意义且使重构误差最小的丰度数据。
AAENet 框架中判决器各神经元具体细节如表2 所示,所用的判决器LossD和生成器LossG的损失熵函数可以依次表示为以下形式:

表2 判决器网络层架构及激活函数Table 2 The layer type and activation function used in the discminator
式中,yi表示为输入像元值,表示经由自编码器的重构像元值。同时,在自编码器的重构误差上,本文以光谱角距离(SAD)来作为损失函数进行度量。其他基于自动编码器的方法也有采用均方根误差(RMSE)作为重构误差。然而实验中我们发现,RMSE 对数据幅值的大小变化较为敏感,当训练数据发生仅基于其绝对大小进行缩放时,采用RMSE 进行训练可能导致更高的重建误差。而将具有尺度缩放不变性的SAD 作为目标函数可以提供更好的解混性能。值得注意的是尽管这种尺度不变的特性可能会导致估计的端元在幅值的比例上产生变化,但是只要在网络框架中加入了丰度的ASC 和ANC 物理限制,最终获得端元的相对尺度就不会受到影响。此外,为了使自编码器可以更快地收敛,本文在损失函数中对解码器的权重矩阵(端元)加入了一项正则化项。自编码器的损失函数可以表示为
式中,xi,xj分别表示为度量的两个向量样本。由于整个框架的损失可以看做为自编码器的重构误差的基础上加入了生成器和判决器的对抗损失项,因此整个AAENet 框架的损失函数可以表述为以下形式:
式中,LossAE,LossD以及LossG分别由式(8),(6)及(7)所示。
3 实验与讨论
在本文中,我们分别在基于传统算法以及深度网络算法中挑选了近期最新提出的解混方法进行比较,分别为:SCM(Spatial Compositional Model)(Zhou 等,2016),FCLS(Fully Constrained Least Squares)(Heinz 和Chein-I-Chang,2001),NCM(Normal Compositional Model)(Eches 等,2010),DAEN(Su 等,2019)以及uDAS(Ying,2019)。其中SCM 通过充分挖掘图像的局部空间信息,在丰度中加入平滑和稀疏先验约束,进而提升解混的精度。FCLS 为传统基于最小二乘的算法。NCM代表对端元变异进行建模的概率模型算法,DAEN和uDAS为近期提出的基于AE的方法。
在以下实验的实施细节上,AAENet 在判决器中采用了VCA-FCLS算法所求得的丰度图作为网络的先验知识进行初始化,并将其作为网络的真实输入进行对抗训练。由于网络的损失函数中已经加入了对解码器的权重矩阵(端元)的正则化项,为防止网络的过拟合的问题,生成器及解码器的权重则均采用了随机初始值的方法进行初始化。值得注意的是,为了保证各算法的公平比较,以下其他对比算法也均采用了同样的VCA-FCLS算法结果进行丰度及端元初始化(除NCM作为监督算法,需要将整个端元库作为已知输入对端元变异的概率模型进行建模采用)。在丰度误差的定量比较中本文选用了RMSE算法,其数学形式可以表述为
3.1 模拟数据集实验
根据文献(Zhou 等,2018),本文从ASTER光谱库中选择5 个光谱范围为0.4—14 µm 的端元合成了一副大小为60×60 模拟数据集。其端元及RGB图像如图3所示。其中该实验中对于端元的正则化项λ参数设定为0.5。
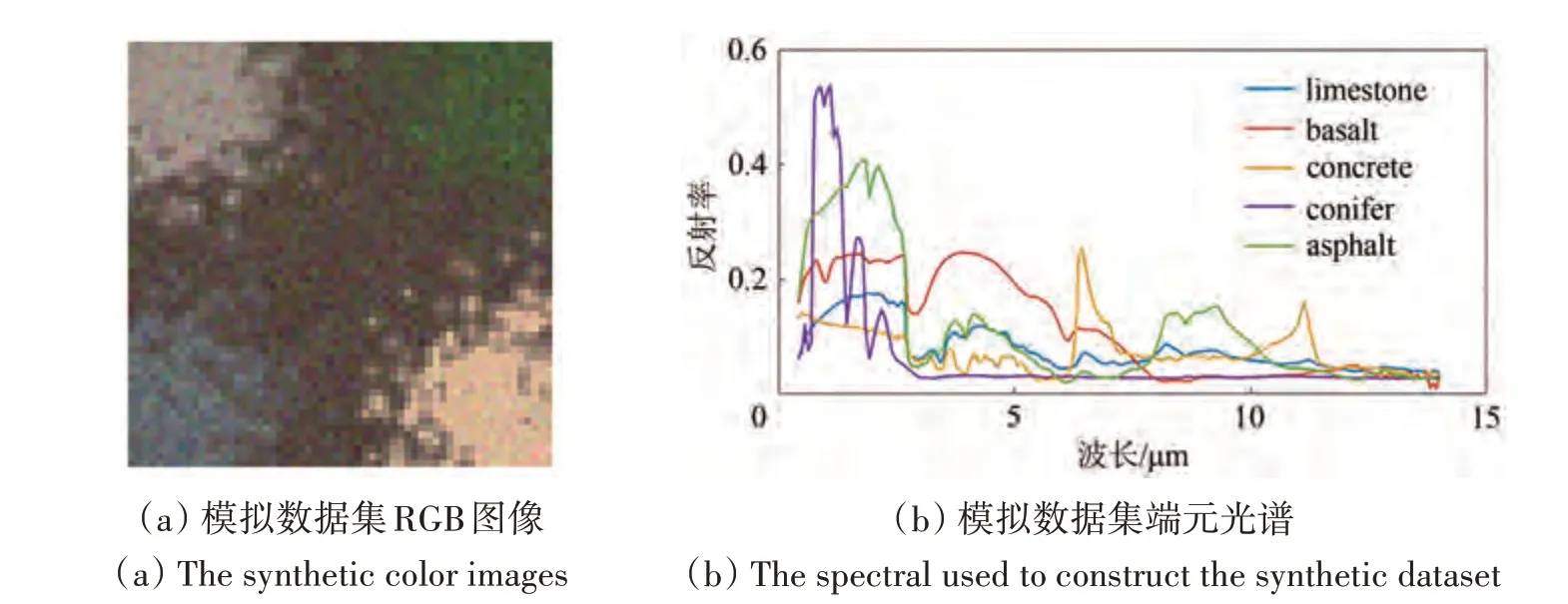
图3 模拟数据集RGB图像及端元光谱Fig.3 The color images and endmembers of the synthetic dataset
图4表示了在该模拟数据集在SNR=20 dB时的各算法丰度对比图。其中AAENet 与其他对比算法中丰度图占优的部分在图中由红色方框标注,可以明显对比看出标注范围内AAENet 的丰度图更加贴近于真实丰度的分布。各算法端元结果SNR=20 dB时的对比如图5中所示。可以很明显的看出在丰度以及端元的解混结果中,AAENet 算法都更加接近模拟数据集的真实数据。
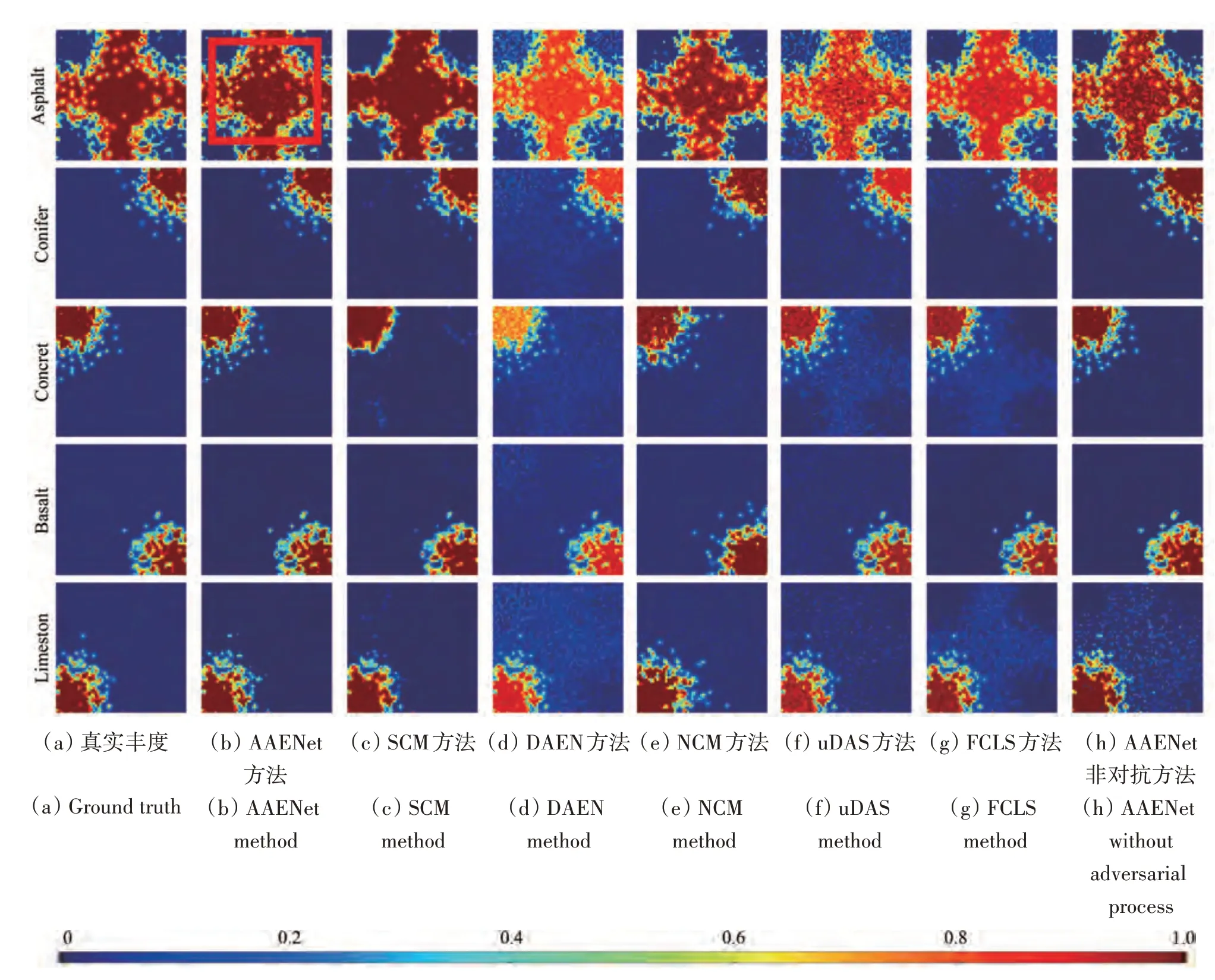
图4 模拟数据集中各算法丰度对比Fig.4 Abundance map comparisons for the synthetic dataset

图5 模拟数据集中各算法端元对比Fig.5 The endmember estimation results for the synthetic dataset
为了验证该方法相对于传统的自动编码器框架的优越性和有效性,在本模拟数据集实验中,我们在去除网络的判决器后,即不采用初始化丰度图进行对抗训练框架时测试了AAENet 的解混性能。最终得到的丰度图的如图4 最后1 列所示(AAENet 非对抗)。对比AAENet 的性能,我们可以清楚地发现在asphalt 及limestone 材料的丰度图中出现了许多离散点和孤立点。由于在初始化实验设置中,所有算法都采用了相同的VCA-FLCS初始化设置,因此我们可以将同样在该初始化条件下传统的自动编码器框架(DAEN,uDAS 及AAENet 非对抗)的解混性能进行对比分析,其不同噪声水平下的丰度及端元的解混定量结果如表3中所示,AANet解混精度均有较为明显的提升。因此,可以证明,将丰度图的初始化值作为丰富的先验知识来通过网络进行对抗训练,可以有效提高网络的性能。
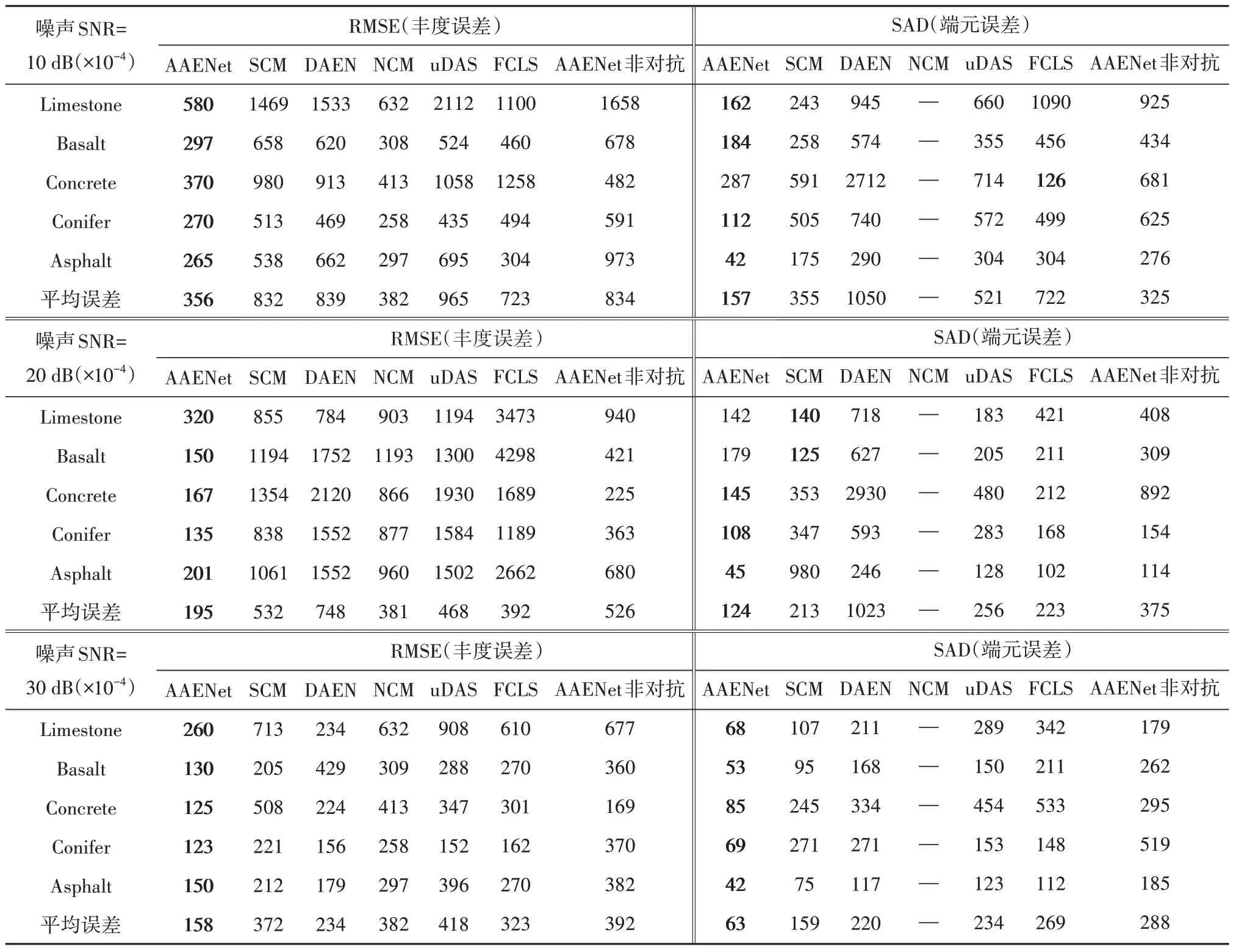
表3 模拟数据集的解混精度对比Table 3 Unmixing evaluation on synthetic dataset
结合表3中信噪比由SNR10 dB至30 dB时的不同算法的丰度及端元的定量误差结果,我们可以分析比较算法在不同噪声下的解混鲁棒性。从表3中可以看出所有的算法当噪声水平相对较高时(SNR=10 dB,20 dB),解混精度都有所下降。这种不稳定性的结果主要与VCA 初始化在不同噪声水平下不稳定有关。由于NCM 需要将整个端元库作为已知输入对端元变异的概率模型进行建模,因此NCM 在不同噪声水平下的性能相对稳定,且作为一种监督算法在进预估端元的对比时未将其考虑其中。对于DAEN算法,观察到其在低噪声水平(SNR=30 dB)下性能相当好。然而,当噪声设置得相对较高时,解混精度下降的较为明显。对于uDAS 算法,由于在网络的构造中加入了去噪约束,因此当信噪比为SNR=30 dB 时,解混精度较高。然而,其整体表现相对较差。AAENet 在各SNR 下丰度估计和端元估计方面都表现出了更高的解混精度及对噪声的鲁棒性,同时也证明了该算法的有效性。
3.2 真实数据集实验
本文选取的真实数据集为大小100×100,光谱范围为0.4—2.5 µm,光谱波段数为198 的jasper 数据集。该数据集由AVIRIS 传感器获取,且包含4种端元(Road,Soil,Water,Tree),其真实丰度图及立体高光谱图如图6所示。其中该实验中对于端元的正则化项λ 参数设定为0.1。此外由于该jasper 数据中缺少真实的丰度及端元的信息进行定量比较,我们与以上对比算法一样,采用(Zhu,2014)中上传的数据作为真实丰度及端元进行定量分析。图7 表示了各算法在jasper 数据集的丰度对比图,其中AAENet 与其他对比算法中丰度图占优的部分在图中由红色方框标注,可以明显对比看出无论是从丰度图的大小形状以及杂乱点分布的情况来比对,AAENet 算法都更加贴切与丰度图真实数据,该数据集RMSE 定量解混精度值在表4中所示。所有的数据都表明在提出的AAENet 网络框架中,通过在自编码器中引入对抗损失,将初始化丰度作为先验知识,能有效地处理现存AE 框架中对噪声和初始化条件不鲁棒的问题,充分发挥深度学习的网络优势从而进一步提高丰度的解混精度。
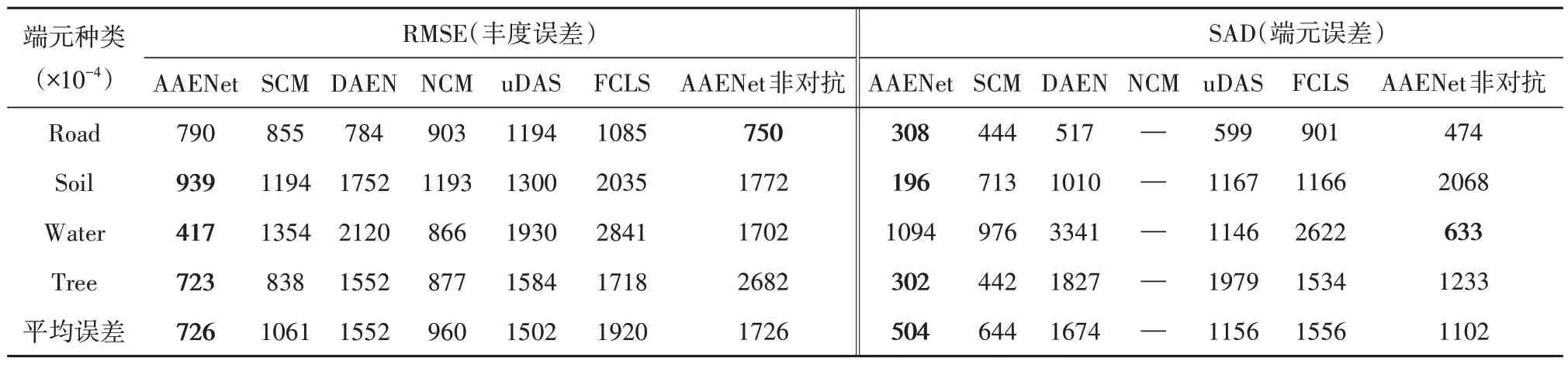
表4 Jasper数据集的解混精度对比Table 4 Unmixing evaluation on jasper dataset

图6 Jasper数据集3D立方图及端元光谱Fig.6 3D cube image and endmembers of the jasper dataset
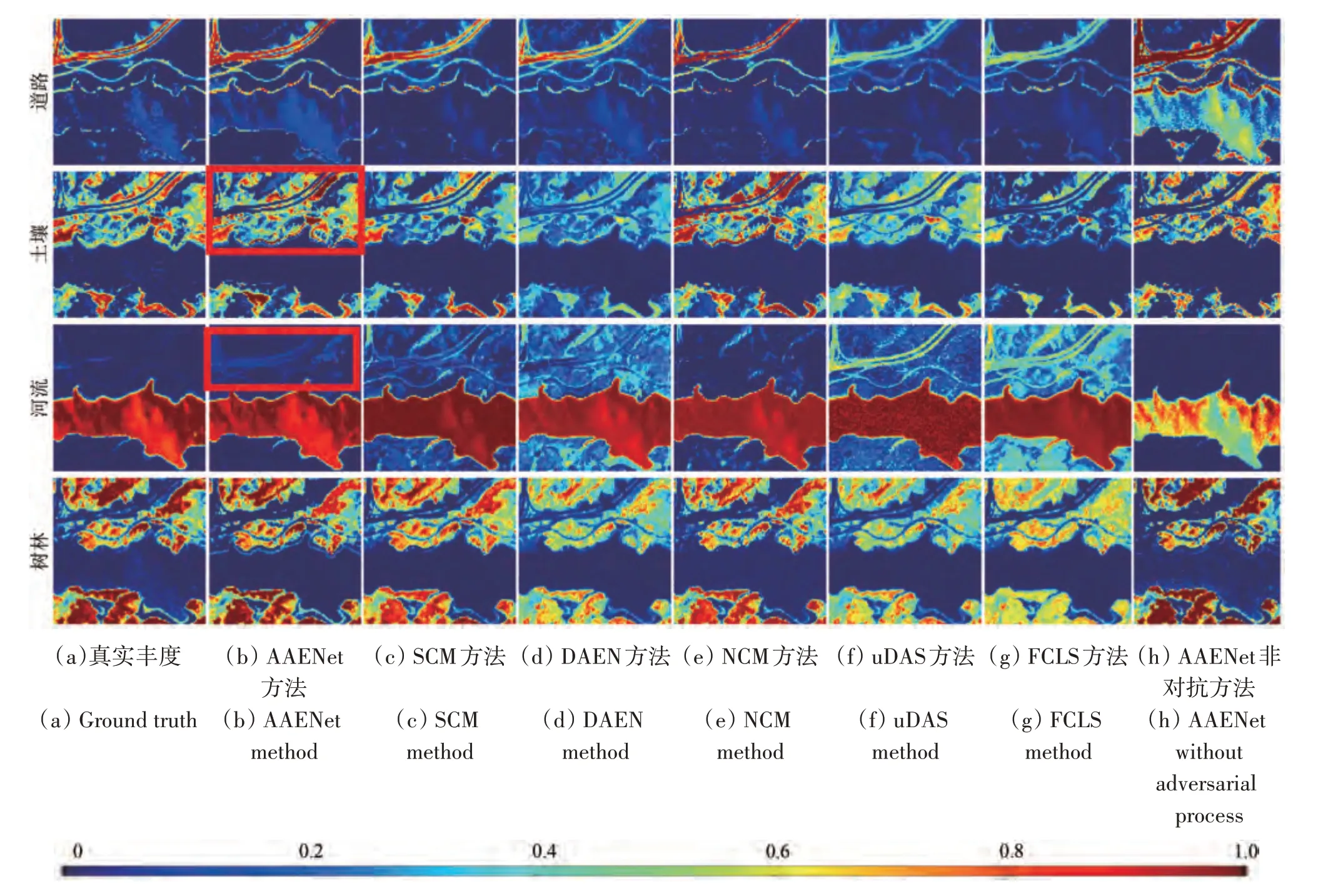
图7 Jasper数据集中各对比算法丰度图Fig.7 Abundance map comparisons for the jasper dataset
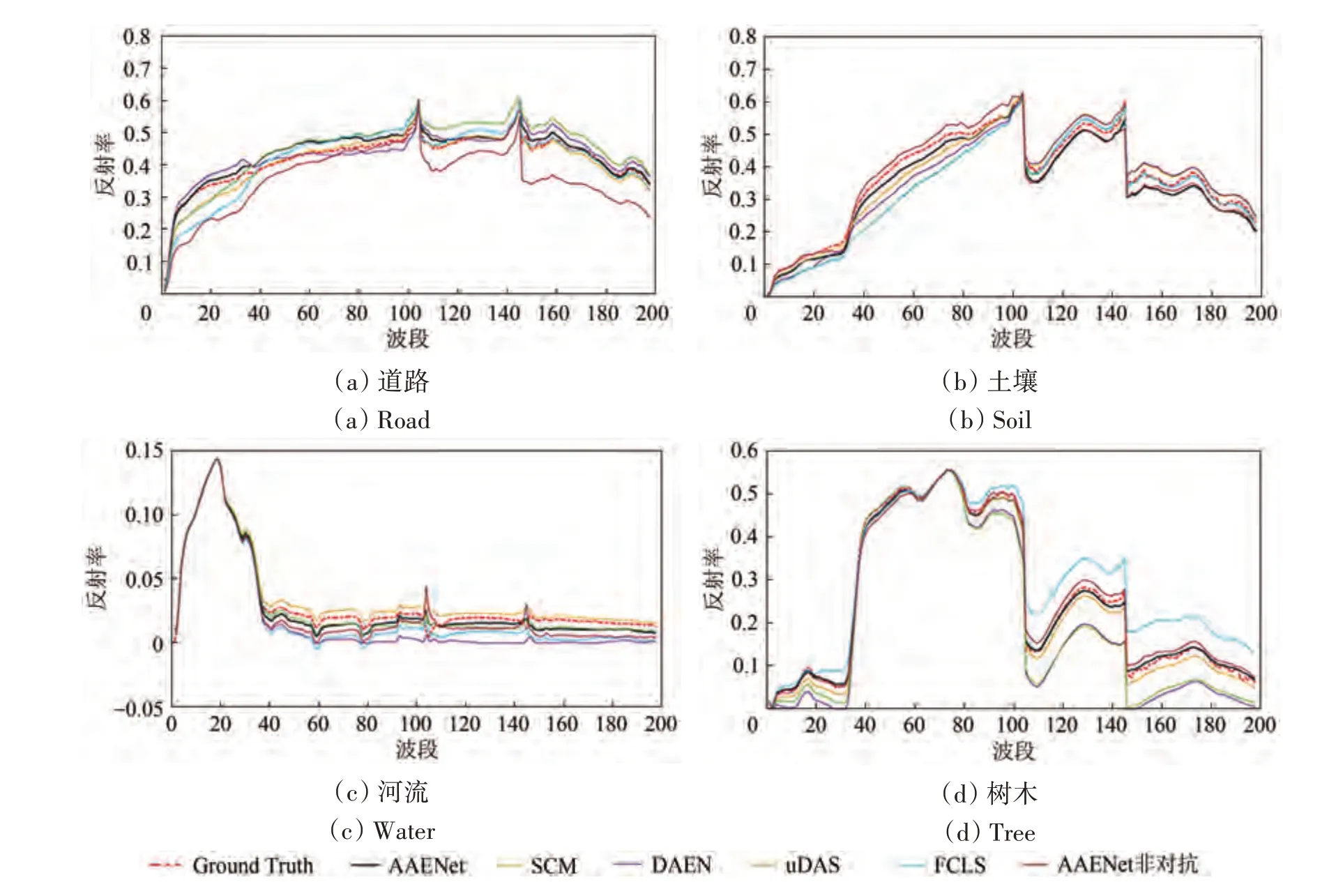
图8 Jasper数据集中各算法端元对比图Fig.8 Abundance map comparisons for the jasper dataset
值得注意的是由于本文为避免网络过拟合而导致的不鲁棒问题,框架的编码层及解码层都采用是的随机值进行初始化。而生成对抗自编码器本身作为一种增强模型其判决器虽相当于提供了一个自适应不同任务和数据集的损失项,但在实际训练过程中收敛速度相对较慢,作者实验发现通过加入端元正则化项可以在一定程度上加快网络的收敛速度。在具体实验中,本文的端元正则化项系数可以在[0,1]的区间内进行取值,由于端元的正则化项采用的是基于纯像素端元提取算法VCA 来提取图像端元,在噪声或混合端元相对较多的图像中,VCA 端元提取方法本身的不稳定性可能会导致端元提取精度较差,应降低该正则化项对网络训练的惩罚,推荐选择较小的端元正则化系数([0,0.5])会得到更好的实验结果。对于图像中存在较多纯净端元且信噪比也较高的图像中,在[0.5,1]区间之间进行取值可以得到更稳定的实验结果。
4 结论
本文提出了一种新的基于对抗式自动编码器(AAENet)的高光谱解混方法,可以有效的同时获取图像的端元特征及其丰度分数。AAENet 主要有两部分构成。第一部分为端到端基于重构误差的解混框架,第二部分是采用对抗性训练的方法,将初始化丰度作为先验知识,生成器和判决器的对抗损失项可以充分学习丰度的先验并加速网络的收敛。在模拟及真实高光谱数据上的实验表明,AAENet 与现有方法相比,该算法具有更好的解混性能与精度。
