基于近红外光谱技术结合改进的CS-BPNN樱桃番茄SSC和Vc含量检测

康明月，罗斌，周亚男，王成，孙鸿雁

（1.中国地质大学（北京）数理学院，北京 100000）（2.北京市农林科学院智能装备技术研究中心，信息技术研究中心，北京 100097）

樱桃番茄是一年生长草本植物，色泽鲜红，口感清甜，具有丰富的营养素，是一种老少皆宜的水果蔬菜。果蔬的内部品质包括硬度、可溶性固形物、糖度、酸度、维生素等成分，其中SSC含量是一项综合指标，是所有溶解于水的化合物的总称，反映果蔬风味品质。樱桃番茄中的Vc含量较高，Vc是一种水溶性维生素，有降低毛细血管的破裂、预防高血压等等功效，体现了番茄的营养价值。因此本文将选择SSC含量和Vc含量对樱桃番茄的品质进行综合评价。

传统的SSC检测方法是用折射仪法，Vc检测方法主要是荧光法、二硝基苯肼法等物化方法。这些方法检测过程复杂，耗时长，难以满足大量果蔬分级分选的要求，因此寻找快速，简便且精准的检测方法具有重要意义。

近年来，近红外光谱技术在食品、医药等领域发展迅猛，该技术摒弃了传统繁琐的物化实验，具有绿色，无损等优点。在果蔬品质检测方面，国内外已有大量研究，郭阳等[1]利用近红外光谱技术结合反向区间偏最小二乘算法预测哈密瓜SSC含量。ÉgeiMárton等[2]通过可见-近红外吸光度和反射率数据估算SSC和番茄红素含量。陈帅帅等[3]为提高可见/近红外光谱对苹果SSC含量的检测精度，利用主成分回归、偏最小二乘法和改进偏最小二乘法三种方法进行比较。上述研究均是利用偏最小二乘回归和主成分回归等线性模型，而有大量研究证明近红外光谱数据与果蔬品质之间存在显著的非线性关系，因此机器学习模型更具优势。机器学习模型中BPNN和极限学习机（Extreme Learning Machine，ELM）最为经典，但其超参数选择和收敛速度等方面有较大的局限性。针对这些问题，纪然仕等[4]采用迭代保留信息变量与基于果蝇算法优化的ELM算法对花椒挥发油含量进行预测，该模型具有较高的收敛性和预测精度，为光谱检测提供新思路。葛春靖等[5]提出GA-BPNN的玉露香梨SSC预测方法，该优化模型预测决定系数达到0.86，可准确检测可溶性固形物。因此采用寻优算法对机器学习方法进行优化有显著优势，但这些算法有参数多，操作复杂等缺点。而杜鹃鸟搜索算法参数少、操作简单、易实现、随机搜索路径优和寻优能力强，且该算法鲜少用于检测樱桃番茄的品质信息。

本文运用近红外光谱分析技术结合BPNN方法和基于杜鹃鸟搜索算法优化BPNN方法开展樱桃番茄内部品质含量的检测研究。杜鹃鸟搜索算法虽有诸多优势，但有全局优化能力弱，收敛速度慢等缺点，因此针对这些缺陷进行改进，引入了改进的杜鹃鸟搜索算法来优化BPNN的方法。在这项研究中，比较多种预处理和特征波长建模方法，以建立基于近红外光谱检测樱桃番茄SSC和Vc含量的预测模型。

1 材料与方法

1.1 材料与仪器

以千禧果、粉圆圣女果、荷兰小番茄和极星农业红色串装小番茄四个樱桃番茄品种为实验对象，均为在超市选购所得。每个品种选取了30个样本，共计120个。

采用型号为BIO-NIRONE-HEM的手持式近红外光谱仪来采集樱桃番茄光谱数据。设置波长测定范围为1 350～1 800 nm，间隔为1.5 nm，扫描时间预计9 s。测量参数为吸光度，每个样本测量三次光谱曲线并取平均值，作为该样本的分析光谱。使用MEMS-FPIShortcut软件，可以将采集的光谱数据文件导入到外部U盘中储存备用。

1.2 内部品质化学测定

1.2.1 SSC测定

将采集完光谱的样品进行榨汁，用绒布擦净2WA-J阿贝折射仪棱镜表面后，取2～3滴汁液在中央，闭合棱镜，调节视度圈，使得视野分为明暗两部分，且明暗界线在十字交叉点上，测定并读数，从而通过折射仪法[6]获得样品的SSC含量。

1.2.2 Vc测定

利用分析天平准确称量樱桃番茄样品5 g，配制质量分数为1%草酸溶液、2%草酸溶液、0.01% 2,6-二氯酚靛酚溶液和标准抗坏血酸溶液，利用2,6-二氯酚靛酚滴定法[7]进行测定，当染料溶液滴定至淡红色为终点，记录数值，利用1%草酸溶液作为空白对照，利用公式[8]计算数值作为样本的Vc含量。

1.3 数据处理

1.3.1 预处理方法

首先将样本按照三倍标准差剔除异常值后，采用Kennard-Stone（K-S）分类算法[9]将样本按3:1的比例划分为校正集和预测集。由于近红外光谱存在人为或自身的噪声影响，本文采用多元散射校正（Multivariate Scattering Correction，MSC）[10]、Savitzky-Golay卷积平滑（Savitzky-Golay Convolution Smoothing，SG）[11]、去趋势化（De-trending）[12]、变量标准化（Standard Normal Variate，SNV）[13]四种经典的方法进行预处理，提升数据精度。

1.3.2 特征波长选取

光谱间存在大量重复冗余信息，会明显降低模型的计算速度。因此，为提升模型的稳定性，选择两种常用的特征波长选择的方法和一种新兴的特征变量选择方法。特征波长提取方法有稳定性竞争性自适应重加权算法、遗传算法和自动有序因子选择算法[14]。

1.3.3 回归模型

采用BP神经网络、基于杜鹃鸟搜索算法优化的BP神经网络以及改进的杜鹃鸟搜索算法优化的BP神经网络建立樱桃番茄内部品质含量回归模型。BP神经网络在预测时，依赖于初始权值和阈值，将杜鹃鸟搜索算法引入BP神经网络中，避免初始权值和阈值陷入局部最小，同时也可以改进收敛速度。其中杜鹃鸟搜索算法是基于杜鹃鸟的寄生行为[15]和鸟类的Lévy飞行行为[16]。但传统的杜鹃鸟算法全局搜索能力和收敛速度都有待提高，因此本文通过引入自适应算法和变更边界值进行改进。

传统杜鹃鸟算法中的鸟蛋被淘汰的概率Pa固定值0.25，但这不利于局部与全局搜索的战略，经已有研究发现[17]，Pa在0.1～0.75之间随着迭代次数的增加而增大，因此引入自适应策略公式（1）为：

式中：

Pa——鸟蛋被淘汰的概率；

Ni——算法当前迭代次数；

Nim——设定的最大迭代次数。

在传统杜鹃鸟搜索算法中，越界值普遍采用边界值，这丧失了鸟窝不断变化的灵活性，因此提出一种按照随机数的不同处理鸟窝的新方法，这将进一步提高算法收敛性，新方法可由式实现：

式中：

X（i，j）——最新迭代鸟窝的位置；

Ub——边界最大值；

Lb——边界最小值。

流程图如图1所示。

图1 基于杜鹃鸟搜索算法的BP神经网络流程图Fig.1 BP neural network flow chart based on cuckoo optimization algorithm

该算法步骤如下：

（1）初始化鸟巢数n，以及最大迭代次数Niter max；

（2）随机产生n个鸟巢的初始位置，该位置与神经网络的权值和阈值相对应；

（3）计算初始位置的适应度值，其中适应度函数为BPNN中训练集的均方误差；

（4）利用公式（1）计算鸟蛋淘汰率，并不断更新鸟巢，根据公式（2）判断是否越界，从而更新位置；

（5）根据适应度值找到最佳位置；

（6）若迭代次数达到最大，则将最优输出为模型初始权值和阈值，否则返回步骤4；

（7）计算误差更新权值和阈值，对样本含量进行预测。

1.3.4 模型评价指标

校正集效果根据校正集决定系数（R2c）和校正集均方根误差（RMSEC）来评价，校正集决定系数越大，校正集均方根误差越小，校正模型效果越好；预测效果由预测集决定系数（R2p）和预测集均方根误差（RMSEP）进行综合评价，其中预测集决定系数越接近于1，其均方根误差越接近于0，则模型预测性能越好。

1.3.5 数据分析

设置近红外光谱上述参数，选择樱桃番茄的果底和赤道相对的两点作为感兴趣区域，获取光谱数据后，其原始光谱图如图2所示，在Matlab 2019a软件上编写程序对该区域光谱数据进行预处理，特征波长提取和建立预测模型，从而获得光谱预处理后光谱曲线和特征波长提取过程，最终采用Origin 7.5画出建模结果的对比图。

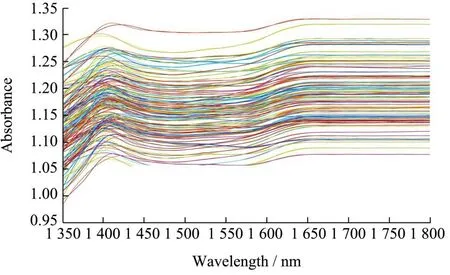
图2 原始光谱Fig.2 Original spectrum

2 结果与讨论

2.1 预处理方法

将原始光谱作上述方法的预处理后，将预处理变量和原始变量分别作为输入变量，内部品质含量作为输出变量，建立偏最小二乘回归[18]。继而选出适合不同内部品质的最优预处理方法。结果如表1。

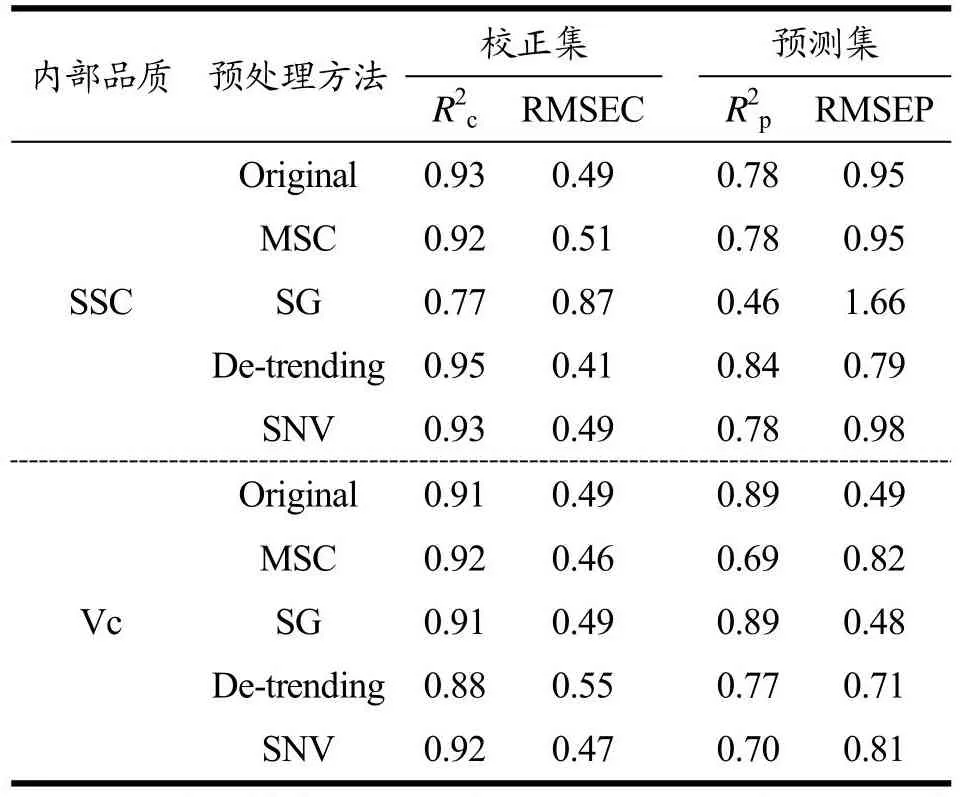
表1 预处理方法比较Table 1 Comparison of pretreatment methods

由表1可知，在预测SSC含量时，去趋势法的R2p最高，均方根误差均低于其他预处理方法，分别为0.95和0.84。去趋势法预处理后的光谱图如图3所示。

图3 SSC最优预处理光谱图(De-trending)Fig.3 SSC optimal preprocessing spectrum (De-trending)

基于原始光谱建立的Vc含量预测模型，Savitzky-Golay卷积平滑在预测集中有显著优势，虽然原始光谱的R2p同为0.89，但RMSEP略低于原始光谱为0.49，因此，Savitzky-Golay卷积平滑为预测的最优方法。经SG算法处理后的光谱图由图4所示。

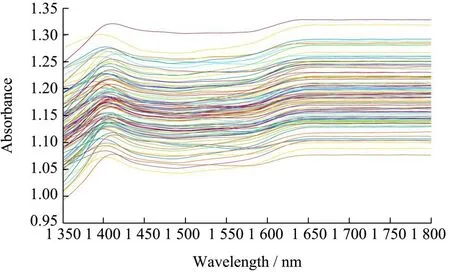
图4 Vc最优预处理光谱图(SG)Fig.4 Vc optimal pretreatment spectrum (SG)

2.2 BP神经网络建模

采用偏最小二乘方法建模时，校正集结果较好，但预测效果相对一般，因此为减少二者差距，进一步提高预测效果，将最佳预处理变量分别应用SCARS、GA和Auto OPS算法处理，建立的BPNN预测模型如表2所示。设置BP网络训练目标最小误差为0.1，训练次数为1000，训练所要达到的精度为1e-6，学习速率为0.01，训练算法为Levenberg-Marquardt算法[19]。

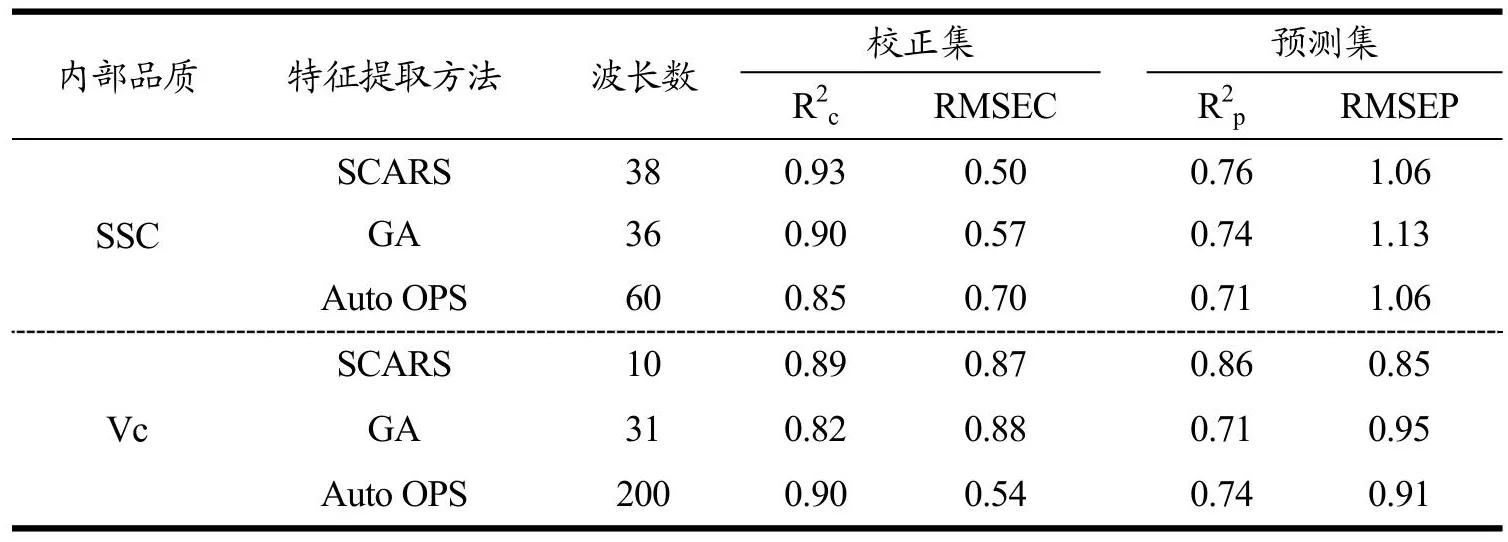
表2 BPNN建模特征变量选取方法比较Table 2 Comparison of BPNN modeling feature variable selection methods

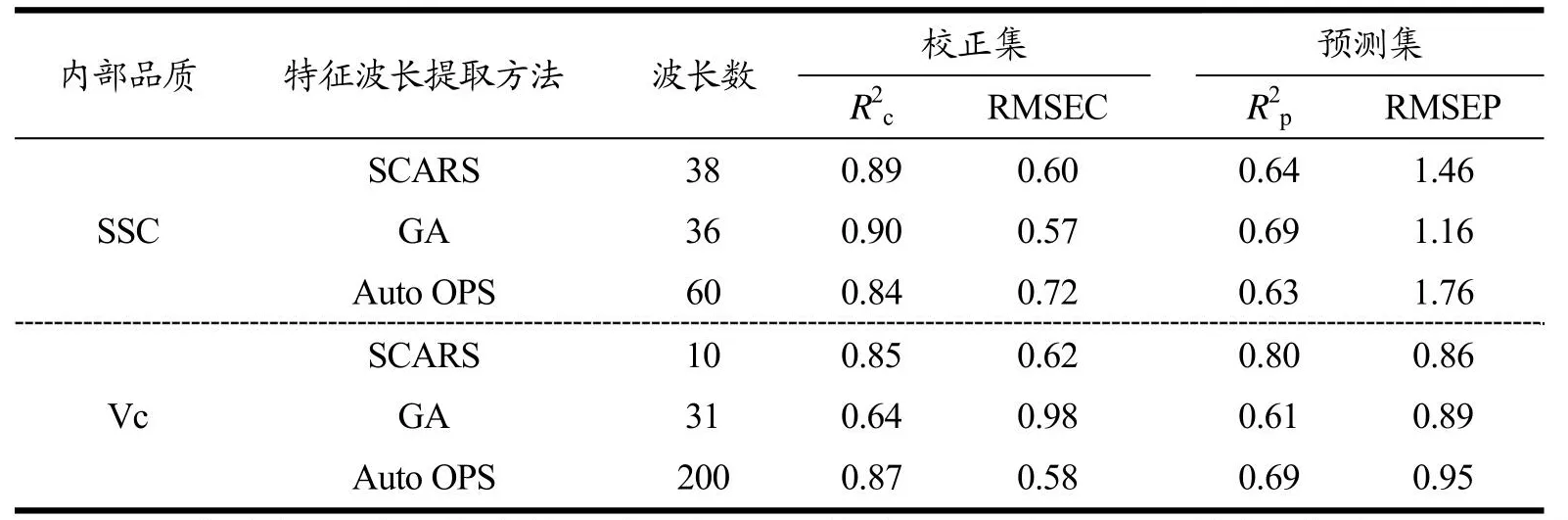
表3 ELM建模特征变量选取方法比较Table 3 Comparison of ELM modeling feature variable selection methods

由表2可知，根据综合评价指标，基于该方法分别建模时，SCARS算法具有显著优势，其波长数基本少于其他方法。当用该算法检测SSC含量时，校正集的决定系数最高为0.93，均方根误差最小为0.50，其预测集的决定系数为0.76，均方根误差为1.06。

应用于樱桃番茄Vc含量测定时，同样是SCARS算法的预测效果最好。其预测精度最高为0.86，远大于剩余GA和Auto OPS两算法决定系数即0.71和0.74。该方法的特征波长提取过程和提取结果如图5和图6所示。从选择结果上看，在迭代到第202次时，交叉验证的均方根误差达到最小为0.76，选择变量数为10个，仅占全波长的3.3%，明显降低模型复杂度。

2.3 极限学习机模型

将最佳预处理变量分别应用SCARS、GA和AutoOPS算法处理后，建立的樱桃番茄内部品质含量ELM预测模型如表2所示。ELM建模时，樱桃番茄SSC含量定义的隐含层神经元个数为35，而Vc含量定义个数为30，采用的隐含层激活函数为Sigmoid函数。

由表2可知，ELM作为机器学习算法的一种，应用于樱桃番茄内部品质含量测定时，SSC含量的R2p均在0.70以下，Vc最高R2p为0.8，预测精度相对一般。基于该方法建模时，SCARS算法具有显著优势，其波长数也少于其他方法。

2.4 CS-BP神经网络建模

由表2、3对比得知，BPNN效果优于ELM算法，因此进一步对BPNN进行优化，以期获得更高的预测精度。杜鹃鸟搜索算法的优点是提高算法的局部和全局寻优，本文初始化鸟巢数n为25，迭代次数为100次，以均方差作为适应度函数。运行结果如表4所示。

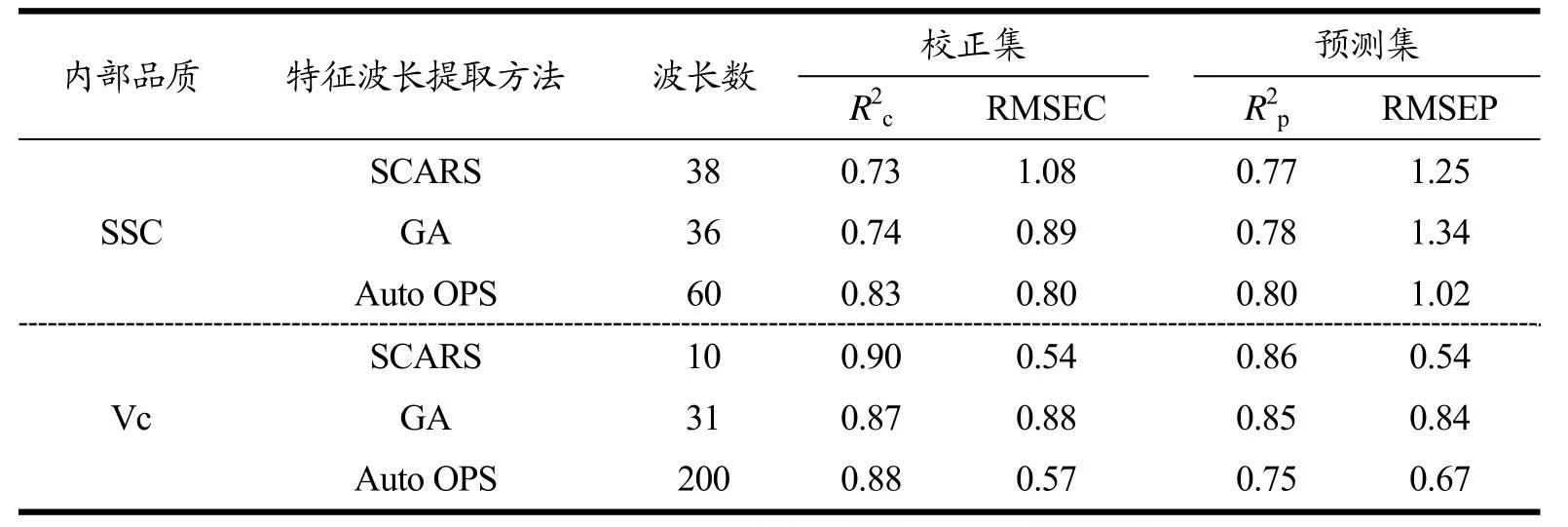
表4 CS-BP神经网络建模特征变量选取方法比较Table 4 Comparison of characteristic variable selection methods for CS-BP neural network modeling

预测SSC含量时，De-trending-Auto OPS-CS-BPNN模型最佳，R2c和R2p分别为0.83和0.80，RMSEC和RMSEP分别为0.80和1.02，迭代曲线如图7所示。当迭代次数为93次时，迭代基本稳定，此时适应度值为0.14，表明预测值和测量值误差逐渐稳定。

图7 杜鹃鸟搜索算法迭代曲线（SSC）Fig.7 Iterative curve of CS algorithm (SSC)

预测Vc含量时，SG-SCARS-CS-BPNN模型最优，R2c、R2p分别为0.90和0.86，RMSEC和RMSEP分别为0.54和0.54。迭代曲线如图8所示。随着迭代次数增加，适应度曲线逐渐平缓，当迭代次数为69次时，迭代基本稳定，适应度值为0.06。

图8 杜鹃鸟搜索算法迭代曲线（Vc）Fig.8 Iterative curve of CS algorithm (Vc)

2.5 ICS-BP神经网络建模

采用改进的杜鹃鸟搜素算法优化BP神经网络方法来预测樱桃番茄的品质含量结果如表5所示。该方法的预测效果较优。

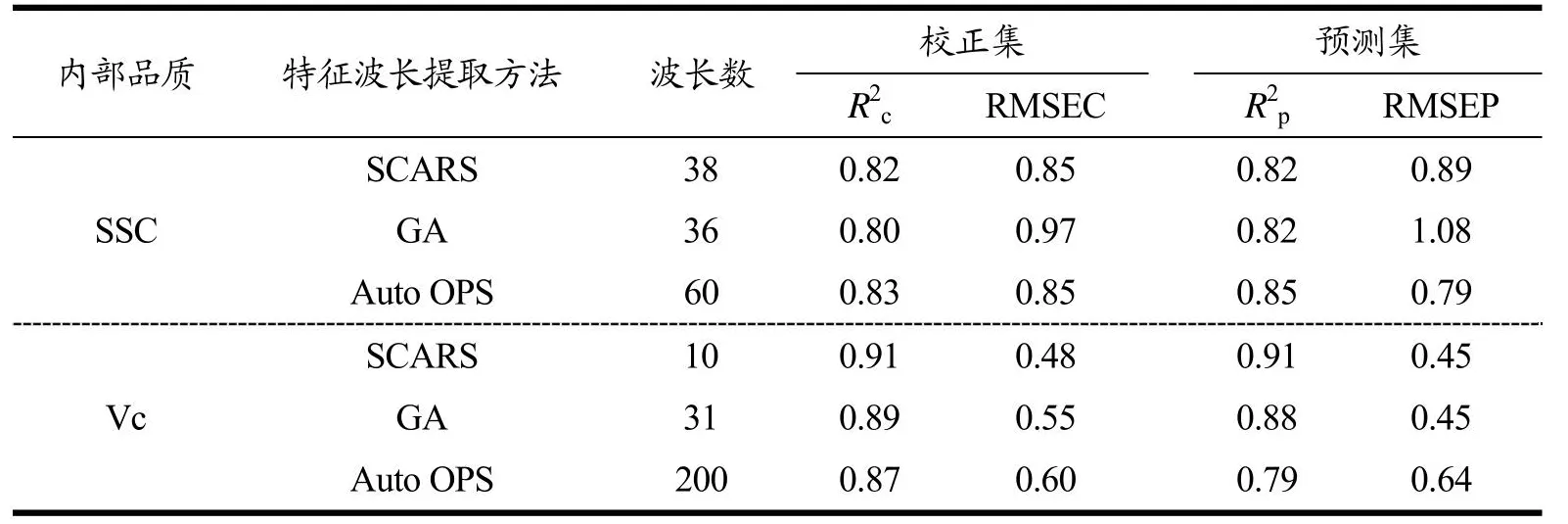
表5 ICS-BP神经网络建模特征变量选取方法比较Table 5 Comparison of characteristic variable selection methods for ICS-BP neural network modeling

综合对比三种不同特征波长提取的建模方法可知，De-trending-Auto OPS-ICS-BPNN模型建立的樱桃番茄SSC含量预测性能最优，其预测精度为0.85，De-trending-SCARS-ICS-BPNN模型次之，De-trending-GA-ICS-BPNN模型最差，其预测精度均为0.82，均方根误差相差0.19。

为防止BP神经网络有过拟合现象[20]，采用的方法是把数据6:2:2的比例划分成三份，分别为Training（训练）、Validation（验证）和Test（测试）。其中Training数据参加训练，其他两部分数据用于检验。在训练进行过程中，目标（Target）即樱桃番茄内部品质含量的化学值和测试（Test）数据之间的误差会越来越小，它们之间的相关系数越接近于1时，效果越好。使用Matlab对模型进行的训练回归效果如图9所示，Training、Validation、Test和All（整体）与目标值的相关系数均在0.87以上。因此可知，De-trending-Auto OPS-ICS-BPNN模型可以作为樱桃番茄SSC含量的预测模型。

图9 基于De-trending-Auto OPS-ICS-BPNN模型SSC含量回归效果Fig.9 Regression effect of SSC content based on De-trending-Auto OPS-ICS-BPNN model

用该建模方法预测樱桃番茄Vc含量时，SGSCARS-ICS-BPNN模型效果最佳，预测精度高达0.91，均方根误差相比最小为0.45。对SG-SCARS-ICS-BPNN模型进行的训练回归效果如图10所示，Training、Validation、Test和All（整体）与目标值的相关系数分别是0.97、0.98、0.85和0.96。因此可知，预测值和参考值之间具有较好的线性关系，表明近红外光谱技术对樱桃番茄Vc含量的检测是可行的。

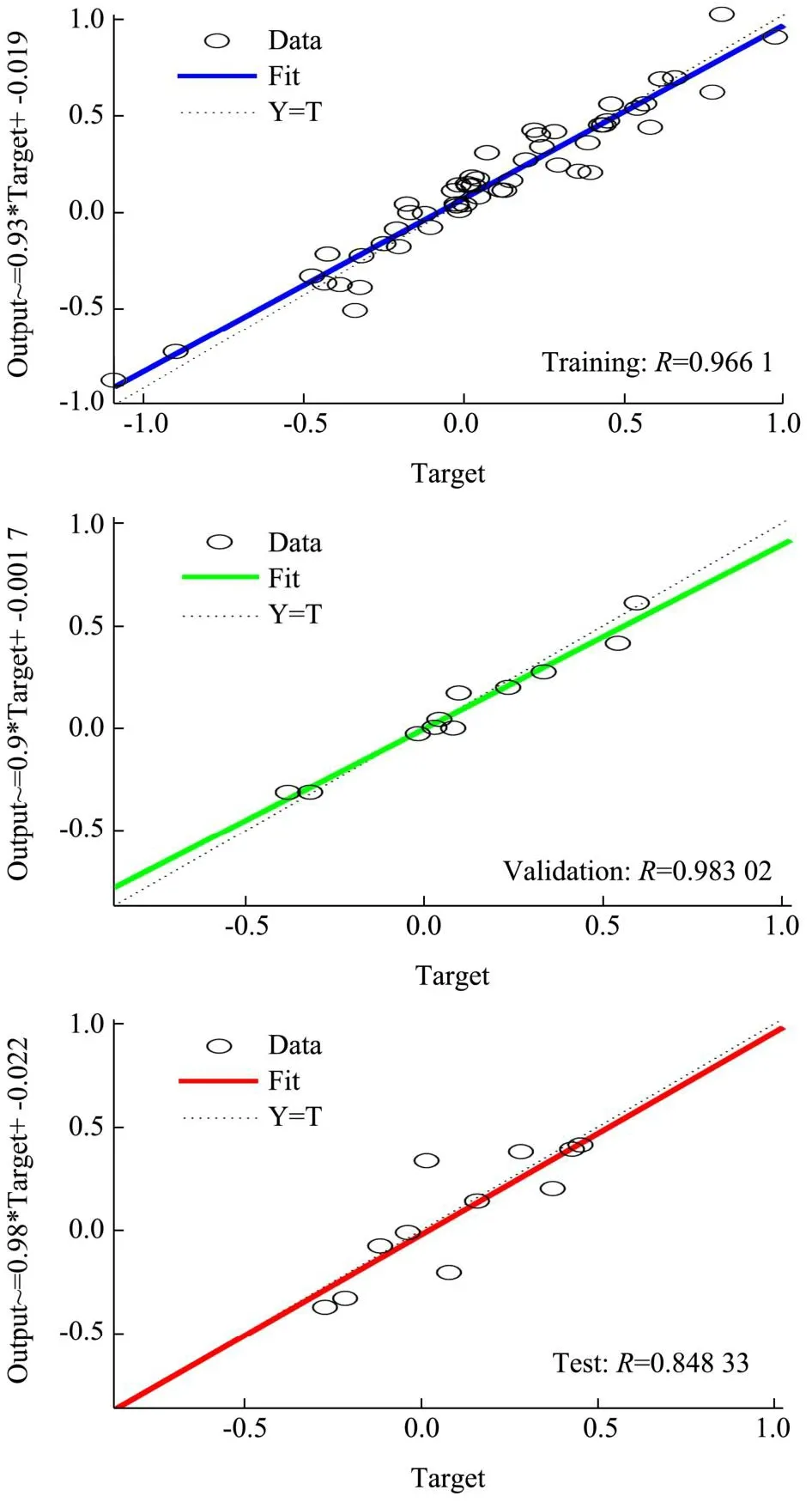
图10 基于SG-SCARS-ICS-BPNN模型Vc含量回归效果Fig.10 Regression effect of Vc content based on SG-SCARS-ICS-BPNN model

2.6 不同建模方法比较

图11和图12分别为SSC和Vc含量基于不同建模方法，分别选择最优结果的对比结果。X轴以上为预测集R2，以下为RMSEP。柱状的长度对应数值的呈正比关系。从图11可看出，上柱状R2随着模型不同显著提升，下柱状RMSEP显著减小，ICS-BPNN预测集R2达到0.85，相较ELM、BPNN和CS-BPNN分别提升了16%、9%和5%，RMSEP达到0.79，相比ELM、BPNN和CS-BPNN模型降低了0.37、0.27和0.23，所以应用ICS-BPNN时，模型效果最好。从图12可以看出，上柱状R2随着模型不同柱状长度增加不明显，但下柱状RMSEP的柱状长度有明显减小，Vc含量预测集均方根误差从最大值0.85降到最小值0.45。因此，经改进的杜鹃鸟搜索算法优化BPNN模型具有最好的预测效果。

图11 SSC最优模型对比Fig.11 Comparison of SSC optimal models

图12 Vc最优模型对比Fig.12 Comparison of Vc optimal models

3 结论

本文利用近红外光谱技术对四个不同品种的樱桃番茄进行测量，通过多种不同算法建立的樱桃番茄SSC和Vc含量预测模型。同时经过比较分析得出，经改进后的CS-BPNN模型预测精度最高。在SSC含量应用中该模型预测集决定系数达到0.85，预测集均方根误差为0.79；Vc含量应用该模型预测集决定系数高达0.91，预测集均方根误差为0.45。因此，改进的机器学习算法可有效提高检测精度，为樱桃番茄品质检测提供理论依据。