中国经济韧性水平测度、时空演化与区域差异

魏 峰，殷文星

（安徽大学大数据与统计学院，合肥 230601）

0 引言

随着我国改革开放的深入，尤其是在加入WTO之后，中国的地区经济体系已经逐步融入世界范围内的产业体系之中。而一系列的外部冲击与地区经济可持续增长之间产生了矛盾，如何解决这一矛盾，韧性理论为此提供了新视角。把区域经济与韧性理论相结合就产生了经济韧性的概念。在复杂的国际环境与外部冲击不确定性的背景下，经济韧性是一个国家或者地区的经济高质量发展与可持续发展的重要保障，有利于推动中国现代化建设行稳致远。

自2008 年金融危机以及2020 年新冠肺炎疫情以来，经济韧性的话题越来越受到学术界的广泛关注。目前，对于经济韧性的理论研究已不断完善，对于经济韧性的实证研究主要聚焦在测度方法和影响因素研究方面，而相较于丰富的理论研究，实证研究有待深入。Holling（1973）[1]首先把韧性概念引入生态学领域，随后经济地理学沿用了此概念，并在此基础上做出改进和完善。基于演化的思想，Martin 和Sunley（2015）[2]对经济韧性做出了具体的定义，认为经济韧性是区域经济系统面对各种冲击时抵抗或者恢复发展状态的能力，它包含抵抗力、恢复力以及重新定位和更新。这一定义得到了很多学者的认同[3,4]。随着经济韧性的理论研究不断完善，学者们开始对经济韧性进行测度，采用的方法包括指标体系法与敏感性指数法。谢会强等（2022）[5]通过综合评价指标体系法测度了我国267个城市的经济韧性；Martin（2012）[6]使用敏感性指数法测度了英国各地区的经济韧性，韩爱华等（2021）[7]使用敏感性指数法对疫情下中国各省份的经济韧性进行测度，魏峰等（2023）[8]使用敏感性指数法对新冠肺炎疫情下长三角城市的经济韧性进行测度。

现有研究主要关注经济韧性的理论分析，实证方面大多是对经济韧性进行测度和影响因素分析，而对经济韧性的时空特征、动态演进以及区域差异的研究较少。本文基于2008—2021 年中国31 个省份的面板数据，将研究时期划分为金融危机抵抗期、金融危机恢复期和新冠肺炎疫情抵抗期，利用敏感性指数法测度三个周期的经济韧性水平，采用GIS可视化、标准差椭圆（SDE）与莫兰指数揭示省域经济韧性的时空特征，使用核密度估计和Dagum基尼系数揭示中国经济韧性的动态演进及区域差异来源。

1 研究设计

1.1 经济韧性的测度方法

本文参考Martin 等（2016）[9]的做法，使用反事实的敏感性指数法来测度经济韧性。此方法需要先定义一个预期收缩（经济增速下降）或恢复的量，并认为区域经济发展应与全国的平均变化一致，区域预期的收缩或恢复时期的经济产出变化公式定义如下：

研究时期为2008—2021 年，包含金融危机与新冠肺炎疫情冲击。由于2010 年经济产出增速开始恢复，故将2008—2009 年设定为金融危机抵抗期（第一周期），2010—2019 年设定为金融危机恢复期（第二周期），2020—2021 年设定为新冠肺炎疫情抵抗期（第三周期）。分周期经济韧性的抵抗力与恢复力计算公式如下：

其中，βresist和βrecover分别表示区域经济的抵抗力和恢复力，其值大于0 表示该省份经济韧性高于全国水平，小于0 表示经济韧性低于全国水平。和分别表示区域i在收缩期与恢复期时GDP 的实际变化量，和表示按照国家预期变化速度测度的区域i在收缩期与恢复期时预期GDP的变化量。同时，本文将2008—2021 年整个时间段设置为长期经济韧性指标并按照公式（2）来计算，从而揭示经济韧性的长期动态演进趋势。

1.2 经济韧性的空间特征

1.2.1 标准差椭圆（SDE）

标准差椭圆是一种空间统计方法，能够精确地反映要素空间多方面特征。它运用平均中心、方位角、长轴、短轴等主要参数来定量地揭示要素的空间分布形态，现已被应用于多个领域。标准差椭圆的主要参数计算过程见文献[10]。

1.2.2 空间相关性

本文使用莫兰指数对经济韧性进行空间相关性检验，计算公式为：

对于空间权重矩阵，常用的有0-1 邻接距离矩阵、地理距离矩阵、经济距离矩阵以及地理与经济距离嵌套矩阵。

地理距离矩阵（W1）计算公式为：

其中，dij表示省份i与省份j之间的距离，通过相应省会城市的经纬度坐标计算得到。

经济距离矩阵（W2）计算公式为：

地理与经济嵌套矩阵（W）计算公式为[11]：

其中，0 ≤λ≤1 表示W1和W2所占比重，本文取λ=0.5。地理与经济嵌套矩阵不仅考虑了省份之间地理意义上的距离，而且考虑了经济意义上的关联，更具综合性。因此，本文空间相关性的权重矩阵选择地理与经济嵌套矩阵分析。

1.2.3 经济韧性的动态演进

核密度估计属于非参数估计的方法之一，可以根据经济韧性本身的特性来得到分布形态的信息，无须事先做假定分布，克服了事先指定某个分布形态而导致的误差[12]。常见的核函数有二次核、三角核以及高斯核等。本文采用高斯核函数对经济韧性的分布动态演进进行估计。假设随机变量x是经济韧性水平，其密度函数为f(x)，则点x处的概率密度为：

其中，n为观测值个数，xi表示观测值，h表示带宽，x表示经济韧性水平的平均值，函数K( *) 为高斯核函数。

1.3 经济韧性的区域差异

本文采用Dagum 基尼系数及其分解对经济韧性的区域差异进行度量，并对区域差异来源进行分析。Dagum基尼系数具体公式为:

其中，G为总体基尼系数，Gjj和Gw为子群内部地区j的基尼系数和子群内部基尼系数贡献度。Gjh和Gnb表示地区j与地区h之间的基尼系数和子群间净值差距对总体基尼系数的贡献度。pj=nj/n，，Djh表示地区j与地区h之间经济韧性的相对影响。k表示地区划分个数，n表示所有省份个数，则表示j(h)地区内i(r)省份的指标水平，代表j(h)地区省份个数，表示所有省份经济韧性的平均值。

其中，Gt是超变密度贡献度，1-Djh为超变密度，表示地区的分布函数。

1.4 数据来源

本文选取2008—2021年中国31个省份（不含港澳台）的面板数据，将研究时期划分为金融危机抵抗期、金融危机恢复期以及新冠肺炎疫情抵抗期，分别对三个周期的经济韧性水平进行测度分析。数据来源于国家统计局官网。

2 结果分析

2.1 经济韧性测度结果分析

使用ArcGIS软件将三个周期经济韧性水平的空间分布做可视化处理，如图1 所示。31 个省份中，在金融危机抵抗力期间（第一周期），有20个省份的抗风险能力（抵抗力）在0 以上，内蒙古、青海、陕西、重庆、湖南、湖北、天津是抗风险能力最强的省份。而北京、广东、上海、黑龙江，则最差，这与当时的经济危机状况相吻合。北京、上海和广东是中国最发达的三个省份，金融业也在快速发展，上海和广东受金融危机冲击将更为严重。在金融危机恢复期（第二周期），有15个省份的恢复力超过0。其中，重庆、安徽、西藏、云南、贵州、湖北、福建的恢复能力最好。恢复力较弱的区域多集中在老工业基地的东北地区，与其他地区相比，恢复较慢。在新冠肺炎疫情抵抗期（第三周期），15个省份的抵抗力超过0。山西的抗击能力最强，被列为独立的一组，而其他抗击能力较强的省份则集中在西部地区。湖北、河南和东北地区的省份抗击能力都很弱，尤其是湖北。

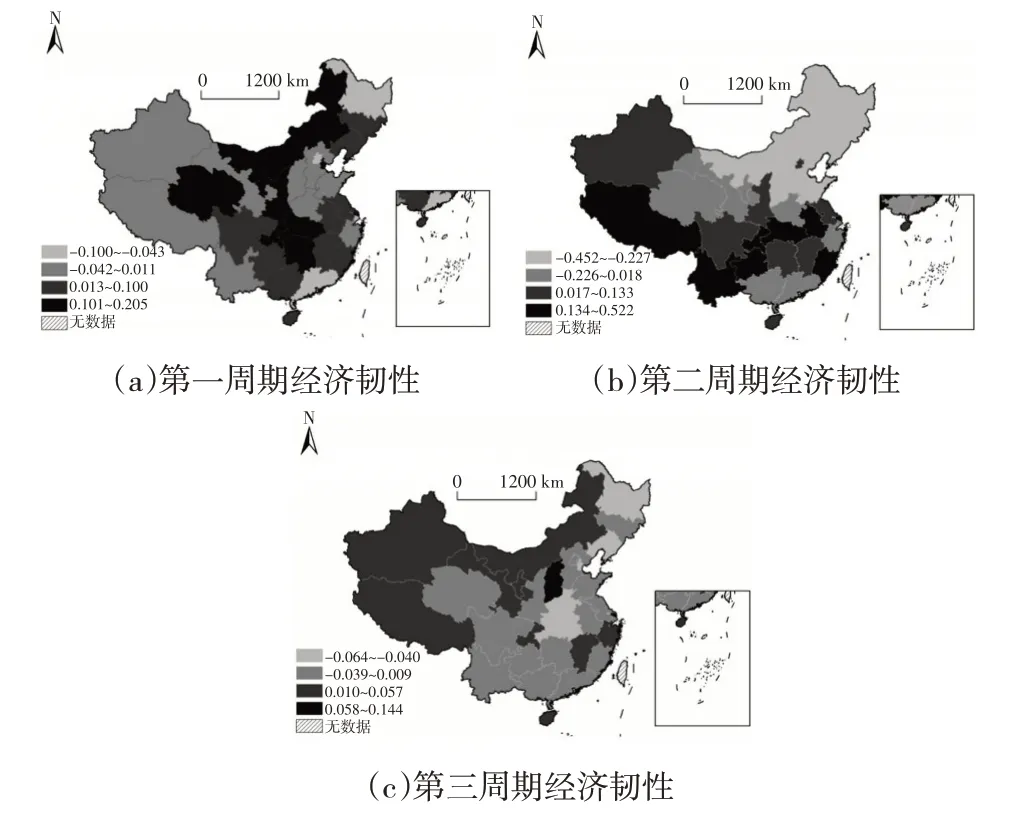
图1 不同周期经济韧性空间分布

2.2 经济韧性空间特征分析

2.2.1 经济韧性的空间格局

使用ArcGIS软件对分周期经济韧性进行标准差椭圆分析，如图2所示。可以看出，金融危机冲击期间，椭圆中心向西南方向移动。第一周期抵抗力空间分布呈现“南（略偏西）—北（略偏东）”格局，而到了第二周期恢复力空间分布呈现“西（略偏北）—东（略偏南）”格局。这表明南方经济韧性的增长整体快于北方，恢复力的空间格局主要分布在南方，北方相对恢复较慢。第一周期到第二周期经济韧性特征方位角从16.597°增加到98.840°，说明了东南方向的经济韧性水平增强更快。新冠肺炎疫情冲击时的抵抗力空间分布呈现“西北—东南”格局，且椭圆的面积相较金融危机冲击的经济韧性明显增大，长短轴的差异也明显变小，方向性变弱，离散程度变得更大。这也比较符合实际情况，新冠肺炎疫情的冲击是全面的、大规模的，所有地区的经济韧性都受到了不同程度的影响。

图2 不同周期经济韧性标准差椭圆分布

2.2.2 经济韧性的空间相关性

全局莫兰指数。使用莫兰指数对31个省份三个周期的经济韧性进行空间相关性检验，结果如下页表1 所示。可以看到，第一周期的经济韧性并不显著，第二周期的经济韧性在1%的水平上显著，第三周期的经济韧性在5%的水平上显著。在金融危机抵抗期，各省份的经济韧性水平之间并没有显著的空间相关性，但在金融危机恢复期呈现正向的空间关联性，由于恢复期地区间可以拥有更稳定的地理与经济因素往来，相邻地区会有较为相似的经济韧性水平，呈现高-高集聚与低-低集聚的特征。新冠肺炎疫情冲击是全国范围的，在疫情冲击下中国相邻省份的抵抗力存在着协作和相互帮助的效果，省份之间有着一定团结一致、共同对抗疫情的合力。

表1 经济韧性空间相关性检验

（2）局部莫兰指数。为探究某一特定地区的空间相关性，本文绘制了第二、三周期经济韧性的局部莫兰散点图。由于第一周期的全局莫兰指数不显著，因此不再论其局部相关性。如图3所示，其中，数字1至31为31个省份，分别为北京、天津、河北、山西、内蒙古、辽宁、吉林、黑龙江、上海、江苏、浙江、安徽、福建、江西、山东、河南、湖北、湖南、广东、广西、海南、重庆、四川、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆。可以看出，两个周期的经济韧性中大多省份的莫兰指数点都落在了第一、三象限，表现为H-H型集聚和L-L型集聚的特征。第二周期经济韧性H-H型省份大多分布在南部地区，L-L型省份大多分布在北部与东北地区。第三周期经济韧性H-H型省份大多分布在西部地区，L-L型省份大多分布在北部与东北地区。

图3 第二、三周期经济韧性的局部莫兰散点图

2.3 经济韧性的动态演进

2.3.1 全国整体经济韧性水平的核密度估计

由公式（2）计算出2008—2021年的经济韧性水平，并分析长期经济韧性的动态演进趋势。图4 展示了2008—2021 年中国整体经济韧性的三维核密度分布。可以看出，经济韧性水平核密度函数中心呈现先右移后左移的动态演变，说明全国整体经济韧性水平呈现先提升再降低的趋势，分界点在中美贸易摩擦时间点附近。金融危机后，在冲击后的经济韧性依然能够稳住阵脚，呈现逐渐提升的态势。但中美贸易摩擦对我国的经济韧性水平有一定冲击，加上出现的新冠肺炎疫情的影响，更加恶化了总体经济韧性水平。波峰高度表现为“下降—上升—下降”的演变趋势。但整体上波峰高度降低、宽度增加，说明各省份经济韧性水平差异程度有扩大的趋势。此外，经济韧性核密度曲线整体上存在右拖尾现象，说明地区间经济韧性差异较明显。

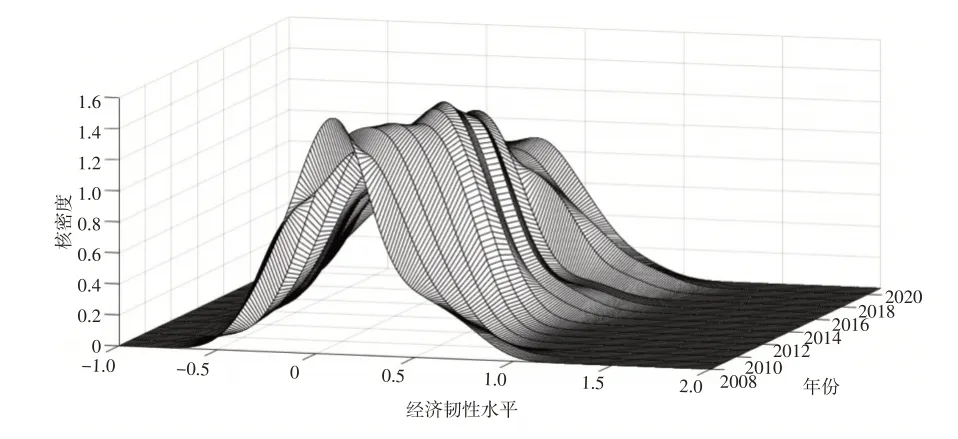
图4 全国整体经济韧性水平核密度分布

2.3.2 分区域经济韧性水平的核密度估计

东部地区的经济韧性的三维核密度分布如图5 所示。东部地区经济韧性水平核密度函数中心呈现先左移后右移的动态演变，说明经济韧性水平呈现先降低后提升的趋势，这与全国整体经济韧性水平的趋势相反。主峰的峰值先降再升，有所波动，但整体峰值在提升，意味着东部经济韧性的差距有扩大的趋势。东部地区经济韧性核密度函数具有明显的双峰，并存在一定的右拖尾现象，说明东部地区经济韧性存在着严重的两极分化态势。

图5 东部地区经济韧性水平核密度分布

中部地区的经济韧性的三维核密度分布如图6 所示。可以看出，中部地区经济韧性水平核密度函数中心呈现向左移动的动态演变，说明经济韧性水平在逐渐降低，这与全国整体和东部地区的经济韧性演变趋势不同。除2008 年之外，主峰的峰值虽有所波动，但总体变化不大，但主峰宽度有所扩大，省际差距有所增加，从波峰数量来看，由双峰过渡至多峰的格局，说明中部地区的经济韧性由两极化转变为多极化趋势。而且中部地区经济韧性水平核密度函数有左拖尾现象，意味着中部地区低于均值的省份较多，经济韧性水平分布不均衡。

图6 中部地区经济韧性水平核密度分布

西部地区的经济韧性的三维核密度分布如图7 所示。由于单一视角展示西部地区经济韧性核密度曲线不够全面，故同时展示左视图和右视图进行分析。可以看出，西部经济韧性水平核密度函数中心呈现先右移后左移的动态演变，说明西部经济韧性水平呈现先提升再降低的趋势，这与全国整体经济韧性的趋势相同。波峰高度和宽度有着先增大再降低的现象，说明西部地区的经济韧性水平的绝对差异呈现再增大后缩小的趋势。另外，西部地区经济韧性核密度函数具有明显的多峰现象，但侧峰较低，意味着西部地区经济韧性存在着轻微的多极分化态势。

图7 西部地区经济韧性水平核密度分布

2.4 经济韧性的区域差异及其分解

上述分析表明经济韧性具有一定的空间异质性，为进一步分析三个周期经济韧性的区域差异及来源，将经济韧性水平进行0-1 规范化处理后使用Dagum 基尼系数分解法对三个周期的区域内差异、区域间差异及超变密度进行测度，结果如表2所示。

表2 三个周期经济韧性区域差异分解及来源

2.4.1 总体差异

整体上，总体基尼系数先增大再缩小，我国经济韧性的差异呈现“倒U”型态势。在贡献率方面，区域间、区域内以及超变密度的贡献率差距不大，都是我国经济韧性发展不平衡的主要来源。具体到每个周期来看，第一周期区域间差异贡献最大，区域内差异贡献最小；第二周期超变密度贡献最大，区域内差异贡献最小；第三周期超变密度贡献最大，达到了50.488%，说明区域间样本交叉问题对总体差异的影响最大，对总体差异的解释达到了一半。可以发现，区域内差异和区域间差异对总体差异的贡献在逐期减小，而超变密度的贡献在逐期增加，说明不同区域间发展的交叉重叠现象逐期明显，经济韧性极化现象加重，因此要解决经济韧性发展不均问题应以缩小区域间发展的交叉重叠程度为重点。

2.4.2 区域内差异

由东、中、西部地区内部基尼系数的演变来看，东部地区的内部经济韧性差异在逐渐收敛，而中部的内部经济韧性差异在逐渐增大，基尼系数从0.202 提升到0.550，通过联合国开发计划署等对基尼系数值的规定，当基尼系数介于0.4～0.59时表示不均衡程度高，因此中部地区的经济韧性不均衡程度从低转高。可能是因为新冠肺炎疫情冲击首先在湖北省武汉市爆发，其在新冠肺炎疫情抵抗期的经济韧性极差，导致中部地区的经济韧性发展变得分布差异较大，从而使得基尼系数激增。西部地区的经济韧性差异呈现波动的态势，先升再降。对比区域内部差异，计算各区域内基尼系数均值发现，中部地区内部差异最大，东部地区次之，西部地区内部差异最小，表明西部大开发的大力推行有助于西部的经济韧性发展和高质量发展。

2.4.3 区域间差异

从区域间的基尼系数演变过程来看，不同区域间的差异演变趋势有较大差异。东-中部的基尼系数在逐期增大，由0.312增加到0.446，增加幅度为42.945%；东-西部的基尼系数与东-中部相反，在逐期减小，由0.342 减小到0.226，减小幅度为33.918%；中-西部的基尼系数在逐期增大，由0.234增加到0.414，增加幅度为76.923%。由此可以看出，中部地区的经济韧性与西部和东部地区差距在增大，特别是与西部地区之间，差距增加幅度接近一倍，因此需要对中部地区经济韧性水平的提升产生重视，防止区域间的经济韧性差距进一步拉大。从区域间差异来看，由东-中部、东-西部、中-西部三个周期的基尼系数均值发现，东-中部的最大，为0.372，东-西部最小，为0.299，这意味着东-中部的经济韧性水平之间差异最大。

3 结论

本文基于2008—2021 年我国31 个省份的面板数据，将研究时期划分为金融危机抵抗期、金融危机恢复期和新冠肺炎疫情抵抗期，利用敏感性指数法测度三个周期的经济韧性水平，采用GIS 可视化、标准差椭圆与莫兰指数揭示省域经济韧性的时空特征，使用核密度估计和Dagum基尼系数揭示中国经济韧性的动态演进及区域差异。得出如下主要结论：

（1）在金融危机抵抗期（第一周期），经济韧性较高的省份主要分布在中部地区，北京、广东、上海、黑龙江抵抗力较差；在金融危机恢复期（第二周期），经济韧性较高的省份地区主要分布在中西部地区，低恢复力省份主要分布在东北地区；在新冠肺炎疫情抵抗期（第三周期），经济韧性较高的省份主要分布在西部地区，湖北、河南和东北地区的抵抗力较差，尤其是湖北。

（2）伴随着不同类型的冲击，中国省域经济韧性的空间分布特征发生相应变动。第一周期抵抗力空间分布呈现“南（略偏西）—北（略偏东）”格局，而到了第二周期，恢复力空间分布呈现“西（略偏北）—东（略偏南）”格局。第三周期的抵抗力空间分布呈现“西北—东南”格局。另外，第二周期与第三周期的经济韧性存在显著的空间相关性，第一周期的经济韧性没有显著的空间相关性。

（3）对于长期经济韧性而言，全国整体经济韧性水平呈现先提升再降低的趋势，分界点在中美贸易摩擦时间点附近。与全国整体经济韧性水平的趋势相反，东部地区经济韧性水平呈现先降低后提升的趋势，且存在较为严重的两极化现象。中部地区经济韧性水平在逐渐降低，而且中部地区经济韧性水平低于均值的省较多，经济韧性水平分布不均衡。西部经济韧性水平呈现先提升再降低的趋势，且存在着轻微的多极分化态势。

（4）中国经济韧性的总体差异先增大后缩小，呈现“倒U”型态势，超变密度即不同区域间发展的交叠现象逐渐成为我国经济韧性发展不平衡的主要来源。东部地区的内部经济韧性差异在逐渐收敛，而中部地区的内部经济韧性差异在逐渐增大，西部地区的经济韧性差异呈现波动的态势，先升再降。中部地区内部差异最大，东部地区次之，西部地区内部差异最小。中部地区的经济韧性与西部和东部地区差距在增大，特别是与西部地区之间的差距增加幅度接近一倍，东-中部的经济韧性水平之间差异最大。