磁悬浮转子不平衡振动控制研究

李 雪 李峰岩 胡叨福

（1.珠海格力电器股份有限公司 珠海 519070；2.广东省高速节能电机系统重点实验室 珠海 519070）

引言

磁悬浮轴承由于无摩擦磨损、高转速、低功耗等优点在现代工业被广泛应用[1-3]，从机械振动系统角度，磁悬浮转子在不平衡力作用下产生的受迫振动除了与本身不平衡量有关，还取决于系统的控制器形式。目前，大量针对磁悬浮转子不平衡振动控制的研究文献可归纳为两个方向，其控制目标分别为振动位移最小和惯性力最小。

振动位移最小补偿：蒋针对不平衡补偿提出一种基于振动系数识别的方法，但该方法只在恒定频率处进行实验，动态升频没有相关描述且实现复杂[4]。Matras 提出一种自适应不平衡振动抑制方法，但权重矩阵的选取比较困难，并且算法的收敛速度有待提高[5]。

惯性力最小控制：刘基于磁悬浮飞轮提出一种惯性力最小控制方法，低速时，基于辨识的转子惯性轴位置消除同频振动力，实现全频率范围内的同频力抑制，但功放的低通特性暂未考虑[6]。高在仿真中通过减小轴承线圈电流实现惯性力最小控制，但是转子悬浮精度大于未施加控制时的悬浮精度[7]。

综上所述，位移最小补偿控制算法普遍相对复杂，实施难度大。惯性力最小控制方法在进入位置控制器作用前消除转子位移信号中的正弦（余弦）分量，即控制器不再产生对正弦（余弦）信号的控制量，使得正弦（余弦）电磁作用力趋于零，减小外部振动，工程化应用前景好。

1 不平衡振动控制分析

建立单自由度磁悬浮系统不平衡力受迫振动控制模型，如图1 所示。

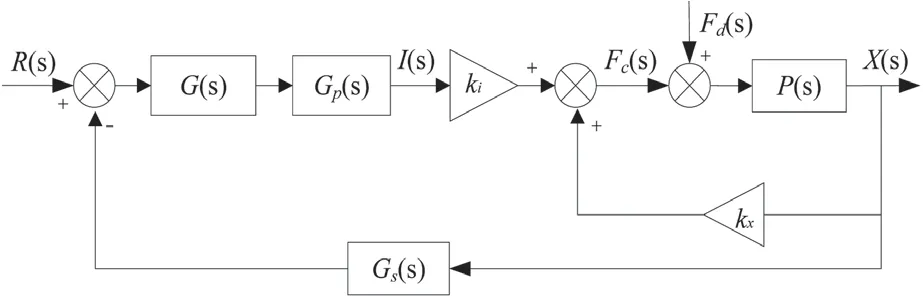
图1 单自由度磁悬浮系统控制框图

将不平衡干扰力作为输入，分别以转子位移、轴承电流作为输出，则有：

式中：

ki—电流刚度；

kx—位移刚度；

Gs(s)—传感器；

G(s)—控制器；

Fc(s)—电磁力；

X(s)—振动位移；

I(s)—控制电流；

Fd(s)—不平衡力；

Gp(s)—功率放大器。

由方程（1）到（3）可知：电磁力与不平衡力方向相反，电磁力控制强弱与控制器性质息息相关。轴承控制电流减小，磁悬浮轴承对转子的控制能力降低，转子趋向于绕惯性主轴旋转。在系统中串联LMS 自适应滤波算法实现不平衡控制便是基于上述原理。

2 基于LMS 自适应滤波的磁悬浮转子不平衡控制

2.1 LMS 自适应滤波器

LMS 自适应滤波器其实质是采用数字信号处理的方法，消除转子位移信号中的与激励频率相同的正弦（余弦）振动分量，使得控制器不对该同频信号响应，从而减小轴承控制电流，降低轴承振动。同时如果转子旋转中心处于转子几何中心和转子质心之间，由于转子趋向惯性轴旋转，作用在转子上的不平衡干扰力也会减小，转子悬浮精度得到提高。

LMS 算法原理框图如图2 所示，算法的控制目标是输出信号y(k)与输入信号中的不平衡信号相抵消，使得误差的均方值最小。

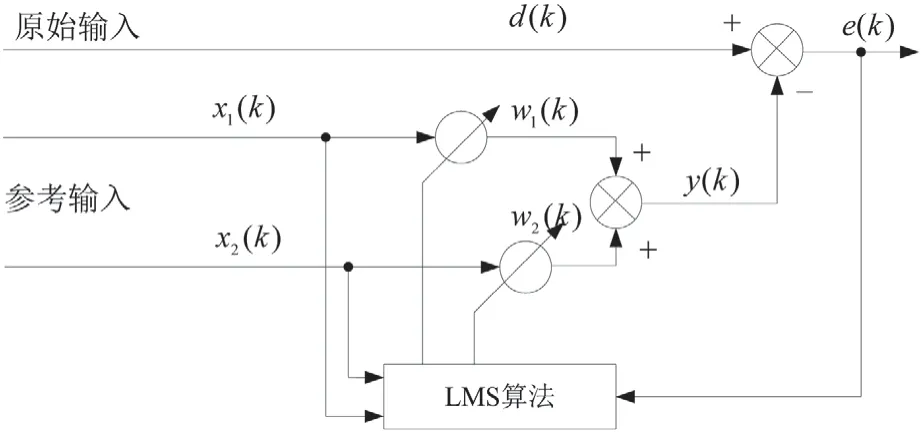
图2 LMS 自适应滤波原理框图

定义LMS 目标函数为J=e(k)2，误差、权系数及参考信号定义如下：

式中：

d(k)—转子位移信号；

e(k)—误差信号；

W1、W2—权系数；

x—正、余弦信号；

ω0—信号角频率。

根据梯度下降法，权系数沿误差性能曲面梯度估值的负向更新，即：

式中：

μ—收敛系数。

取单个误差样本平方e(k)2的梯度(k)作为 ∇ (k)的估计[8]，有：

因此，方程（5）可进一步描述为：

利用上述（4）、（7）方程就可以得到不平衡同频信号y(k)。

对于滤波器来讲，输入为d(k)，输出为e(k)，传递函数表示为：

式中：

Ts—采样时间。

2.2 系统稳定性分析

基于LMS 磁悬浮转子不平衡控制原理框图如图3 所示，LMS 滤波器串联于系统的前向通路中，通过LMS 滤波器的输入输出关系可知，算法的本质也属于陷波器，串联会对系统的传递函数产生影响。

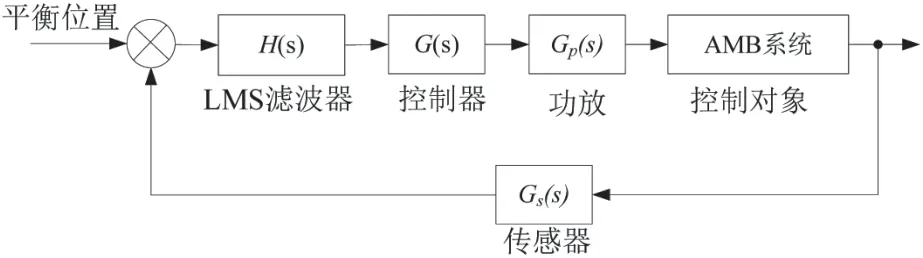
图3 基于LMS 的磁悬浮转子不平衡控制原理框图

LMS 自适应滤波器传递函数为H(s)，对应的开环传递函数为：

此时，闭环传递函数为：

由方程（10）可知，H(s)会导致系统开、闭环传递函数变化，因此将基于对数幅相频率特性稳定判据对磁悬浮系统整体控制结构进行稳定性分析。

图4（a）对应于在小于刚体模态频率处加入H(s)后的控制系统频率特性分析，控制器Gc(s)采用PID 控制，开环传递函数为I 型系统，从相频曲线向上补pi/2 的虚直线，在幅值大于0的频率段，有N-=1.5，N+=1，即N=N+-N-=-0.5。而开环系统有1 个右半平面极点，即P=1，此时Z=P-2N=2，系统无法在此频率范围内稳定运行。

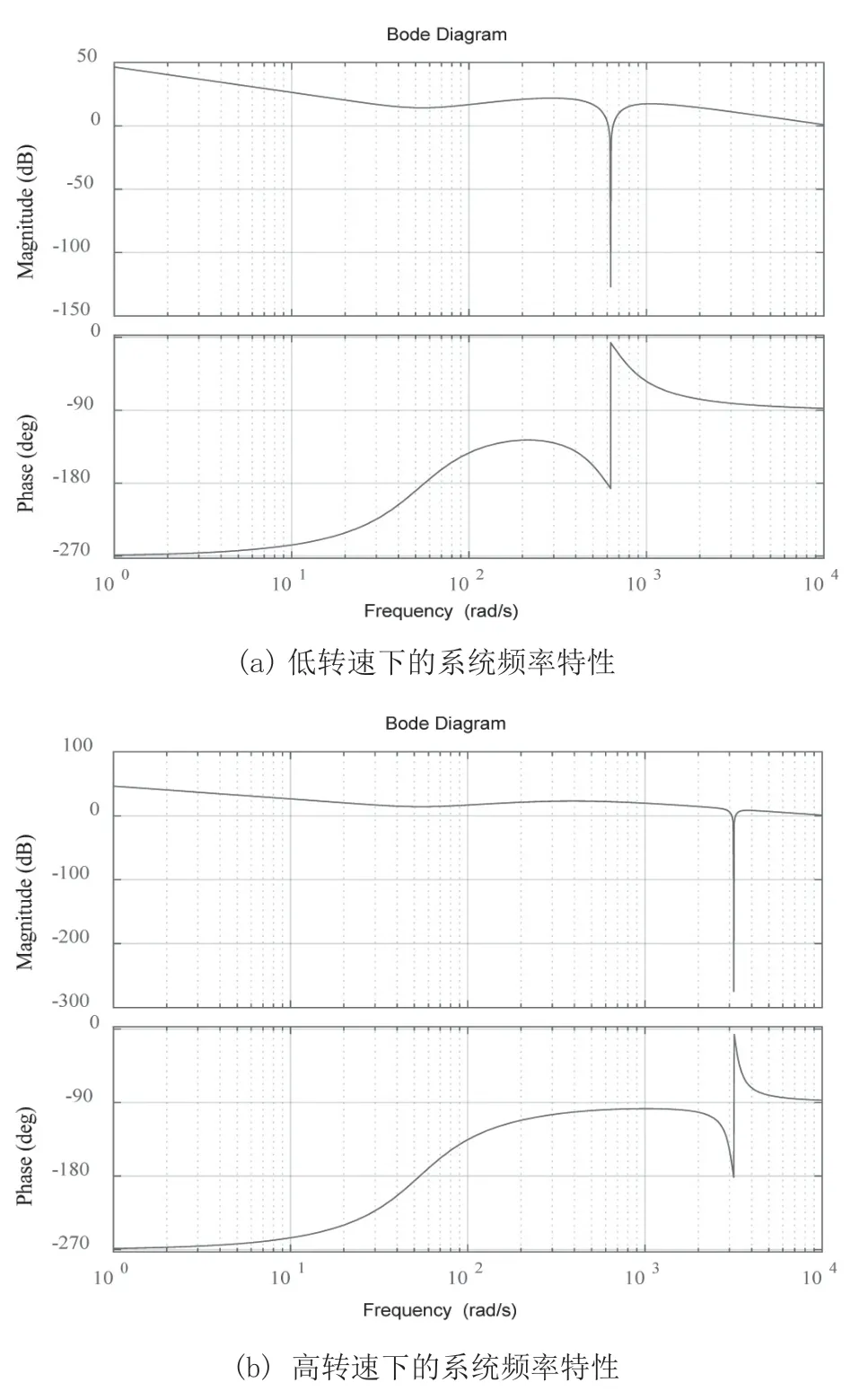
图4 系统稳定性影响分析

图4（b）对应于在大于刚体模态频率处加入H(s)后的控制系统频率特性分析，同理上述分析，在幅值大于0 的频率段，有N-=0.5，N+=1，即N=N+-N-=0.5，此时Z=P-2N=0，系统可稳定运行。

由于低转速下的不平衡力较小及从系统稳定性考虑，工程应用中，通常在刚体模态频率后加入不平衡振动控制算法。

3 仿真与实验验证

基于磁悬浮系统中各环节数学模型，搭建控制系统仿真模型，对不平衡力作用下的控制系统响应及不平衡控制方法进行仿真研究。

仿真给定不平衡力为正弦形式，由图5 中第一条曲线所示可知，转子的振动位移、电流和电磁力都为正弦信号，电流最大为0.7 A 左右，电磁力达到350 N，转子振动位移为20 um。

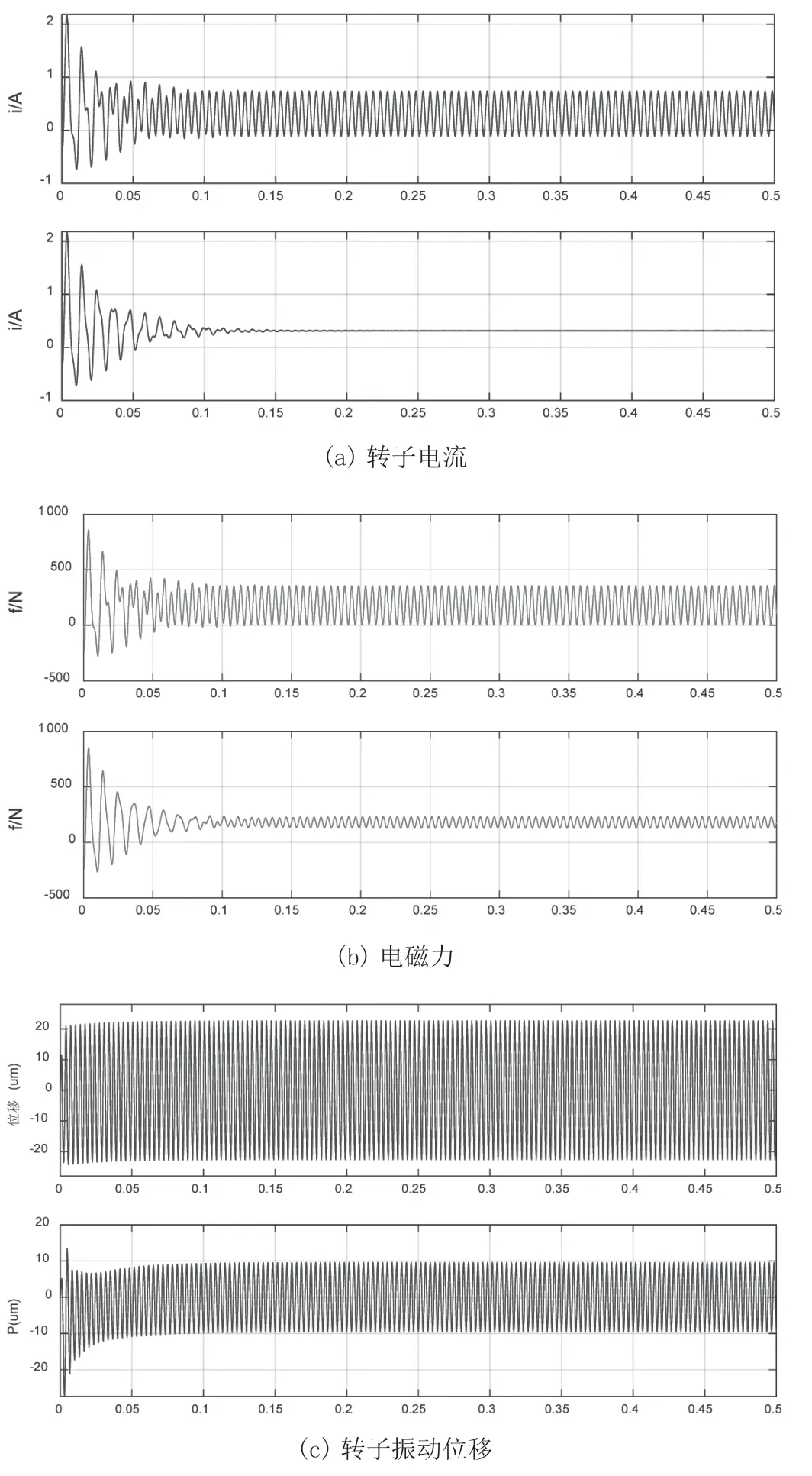
图5 转子电流、电磁力与振动位移对比波形

在大于刚体模态频率时加入H(s)，电流减小到0.3 A 左右，电磁力最大为220 N，转子振动位移为10 um 左右，如图5（a）、（b）、（c）中第二条曲线所示。可见，施加不平衡控制后，轴承线圈同频电流为0，电磁力降低，同时从图5（c）可以看出，当转子趋向惯性轴旋转后，作用在转子上的不平衡力降低，转子悬浮精度得到提高。

在磁悬浮压缩机平台上对不平衡振动控制效果进行验证，算法在大于刚体模态频率的稳定运行频率段加入。图6 中，红色曲线代表轴承电流，黄色曲线为转子振动位移，轴承电流相比正常运行减小了约90 %，转子振动位移减小，与仿真结果一致。

图6 不平衡振动控制实验效果

4 结论

本文基于LMS 自适应滤波器实现了大于刚体模态频率处的磁悬浮转子不平衡振动控制，LMS 自适应滤波算法可以快速实现同频信号的提取，保证了滤波的实时性，不平衡控制方法能够有效地抑制转子的不平衡振动，减小系统功耗，提高转子悬浮精度。