智能晾衣机托架的理论力学建模及优化设计

周 亮

（广东好太太科技集团股份有限公司 广州 511434）

引言

随着我国经济的快速发展，人们对于生活水平的要求也越来越高，电动晾衣机作为一种新型的、便利的物品也逐渐进入人们的生活当中。这种集遥控升降、LED照明功能为一体的产品正改变人们的日常生活，成为阳台上的一件必备品[1]。

托架作为晾衣机的重要组成部分承担着承重和防止摆动、防偏差的功能。托架的主要结构分为托架主体及折叠结构。托架主体作为受力主体承载着晾杆上竖直方向的力并保持不变形，同时托架的折叠结构能在晾晒的杆子上升到顶部时，收拢成紧凑的结构方式，而在晾晒的杆子下降到合适晾衣时，其折叠结构需要既能保证晾晒的杆子的受力平衡，又能保证左右稳定性[2]，见图1。

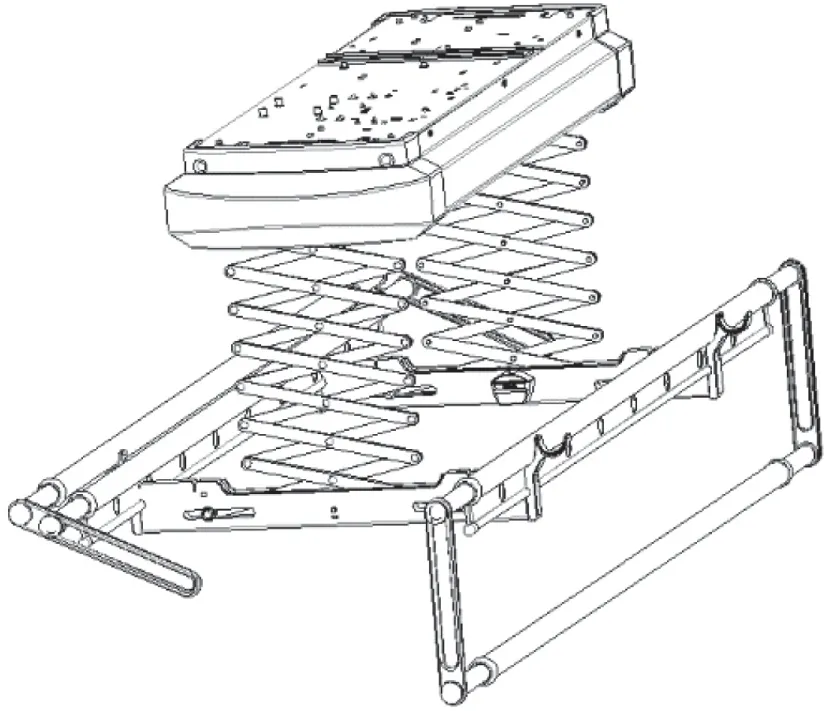
图1 带托架折叠结构的晾衣机

由于设计的不合理和材料应用的不恰当，托架的使用存在性能缺陷或者材料过剩的情况。而折叠结构作为托架的重要组成部分，目前对其进行的研究，多数集中在其作为举升机构或者作为机械执行部件上，如张威[3]等对剪刀架托举升机构的内力场建模研究，胡小舟[4]等对剪叉式举升机构建模及关键参数的研究，罗宁[5]对剪叉式液压升降台速度控制方法和仿真分析，王汝贵[6]等对新型剪叉折展机构的运动性能研究，马骊溟[7]等对剪叉机构铰链耦合模型的分析。目前尚未有相关公开论文针对晾衣机托架进行结构强度方面的研究。随着晾衣机行业的发展，为使晾衣机在满足安全性、可靠性的基础上，优化产品设计以节省产品成本，创造效益，对晾衣机托架进行结构强度理论研究和设计优化变得非常重要。

1 力学分析

1.1 托架整体力学分析

晾衣机具备上升和下降的功能，所以其折叠结构托架折叠部分为运动部件，我们需要研究其所受的力和力学性能在运动中的关系，计算其相关的物理量，从中分析出最优的状况来确定结构参数。

表1 为托架在其运动过程中以及静止状况下各种所需要求输入，其中，材料的尺寸参数与材质等为最初设计参数，我们将进行各项分析后来对其进行优化；

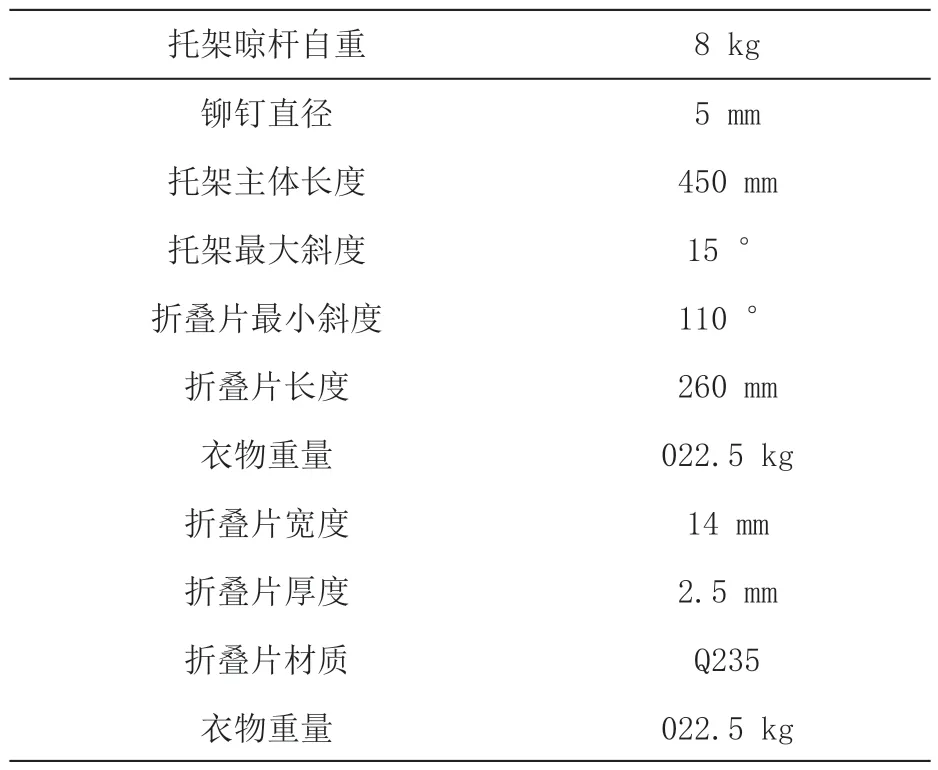
表1 折叠结构托架各项输入参数（初）

根据托架的各项输入参数绘制受力图，如图2、3。

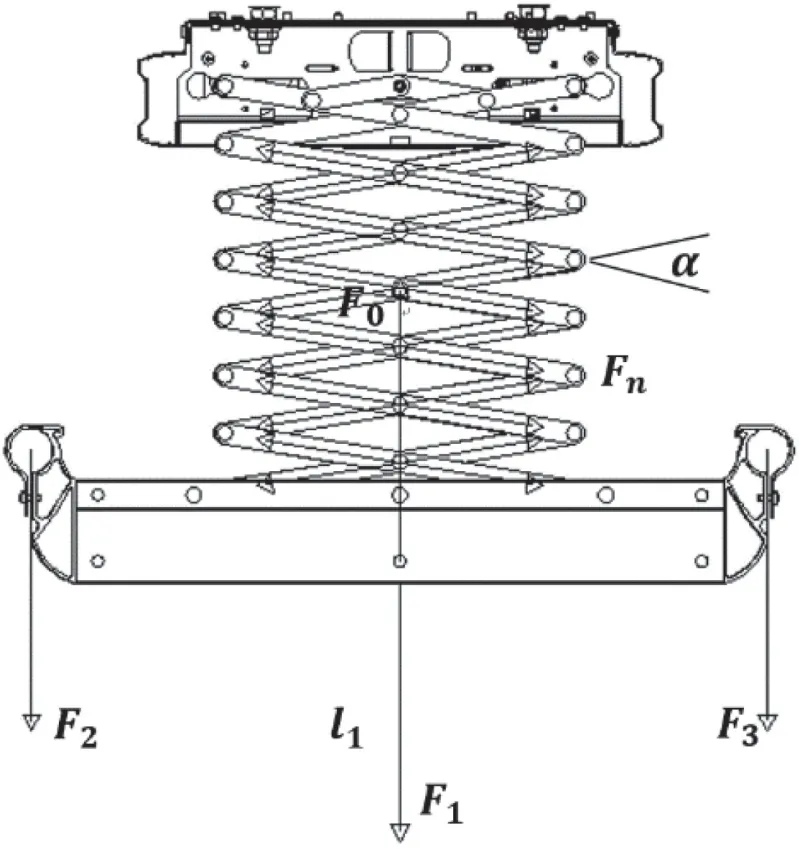
图2 托架折叠结构（平衡受力分析图）

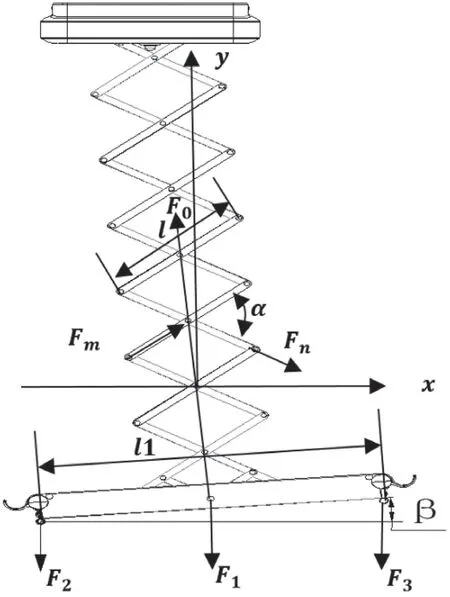
图3 托架折叠结构（单边受力分析图）

晾衣机工作时，作用于托架系统上各种力构成平面力平衡[8]。

式中：

F0—钢丝绳拉力；

F1—托架和晾杆自身的重力；

F2—挂于托架左端的衣物重力；

F3—挂于托架右端的衣物重力；

Fn—托架折叠片轴线拉力；

Fm—托架折叠片轴线推力；

l1—托架主体的长度；

l—折叠片的长度；

α—折叠片的倾斜角度；

β—托架的倾斜角度。

1.2 关键零件的受力方程推导

实验表明，托架失效多出现在托架单边受力不均的情况下，托架失效模式集中表现为三种：钢丝绳断裂失效，折叠片的铆钉受剪失效，折叠片弯曲失稳失效[9]。下面将通过工程力学理论，建立托架单边受力不均时钢丝绳，折叠片铆钉，折叠片的力学方程，研究此三种失效模式。

1.2.1 钢丝绳受力方程

由公式（1）得：

由公式（2）得：

将公式（4）代入公式（5），得到钢丝绳所受拉力F0：

式中：

F0—钢丝绳拉力；

F2—挂于托架左端的衣物重力；

F3—挂于托架右端的衣物重力；

l1—托架主体长度；

l—折叠片长度；

α—折叠片斜度；

β—托架最大斜度。

使用Matlab 软件，绘制出钢丝绳所受拉力F0与折叠片倾斜角度α，托架倾斜角度β 的函数曲线，见图4。

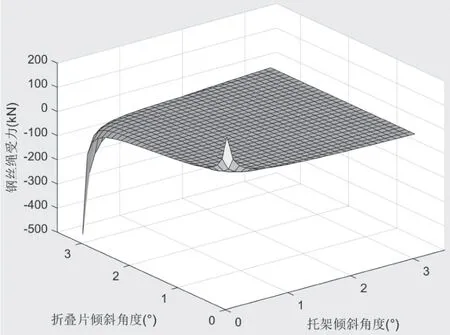
图4 钢丝绳受力与托架折叠片倾斜角度函数曲线

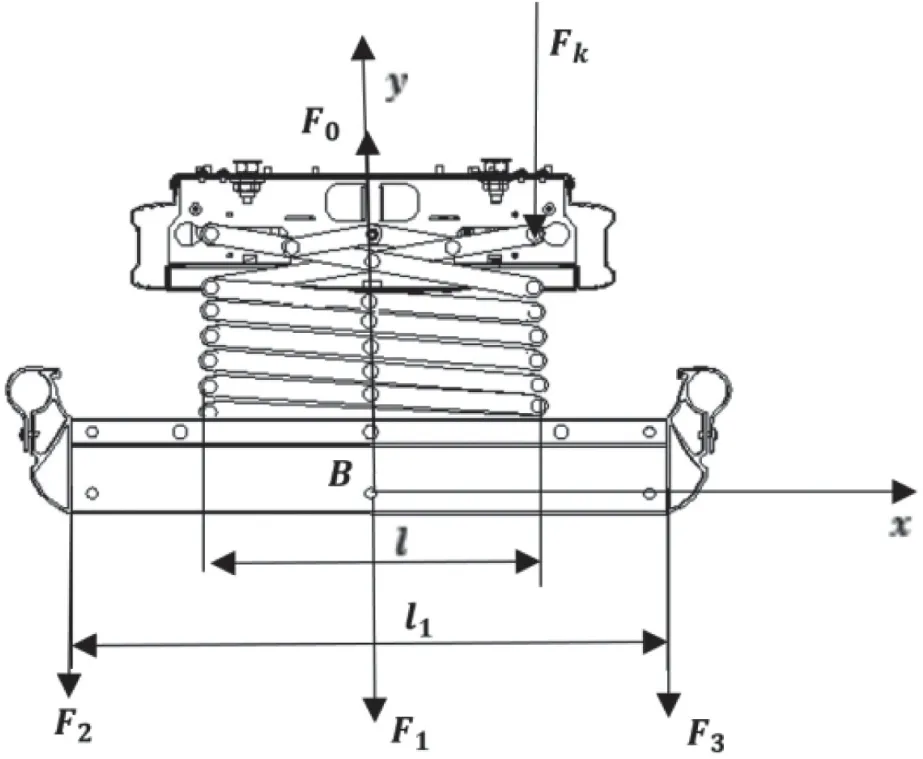
图5 托架收拢状态受力分析

其中，Fk为箱体固定件施加于托架折叠片，使其保持平衡的压力。取B 点为质心：

将（7）式代入（8）可以得出：

式中：

F0—钢丝绳拉力；

F1—托架和晾杆自身的重力；

F2—挂于托架左端的衣物重力；

F3—挂于托架右端的衣物重力；

l1—托架主体长度；

l—折叠片长度。

考虑最极端的受力不均情况，取0，此时得到：

式中：

F0—钢丝绳拉力；

F1—托架和晾杆自身的重力；

F2—挂于托架左端的衣物重力；

l1—托架主体长度；

l—折叠片长度。

钢丝绳目前采用7*7 规格，直径1.5 mm。通过查表2 得，此规格钢丝绳最小破断拉力为1.67 kN。将钢丝绳最小破断拉力代入式（10）的F0，求钢丝绳所能承受的施加于托架的最大不平衡力F2：

为使钢丝绳不失效，施加于托架的不平衡力F2应小于582.8 N。

1.2.2 折叠片铆钉受力方程

取单根折叠杆为研究对象，由式（3）得：

结合公式（4）：

考虑最极端的受力不均情况，F3取0。结合公式（4）公式（12）得：

式中：

Fn—托架折叠片轴向拉力；

Fm—托架折叠片轴向推力；

F0—钢丝绳拉力；

F1—托架和晾杆自身的重力；

F2—挂于托架左端的衣物重力；

α—折叠片倾斜角度；

β—托架倾斜角度。

使用Matlab 软件，绘制铆钉所受剪力Fn与折叠片倾斜角度α，托架倾斜角度β 的函数曲线，见图6。

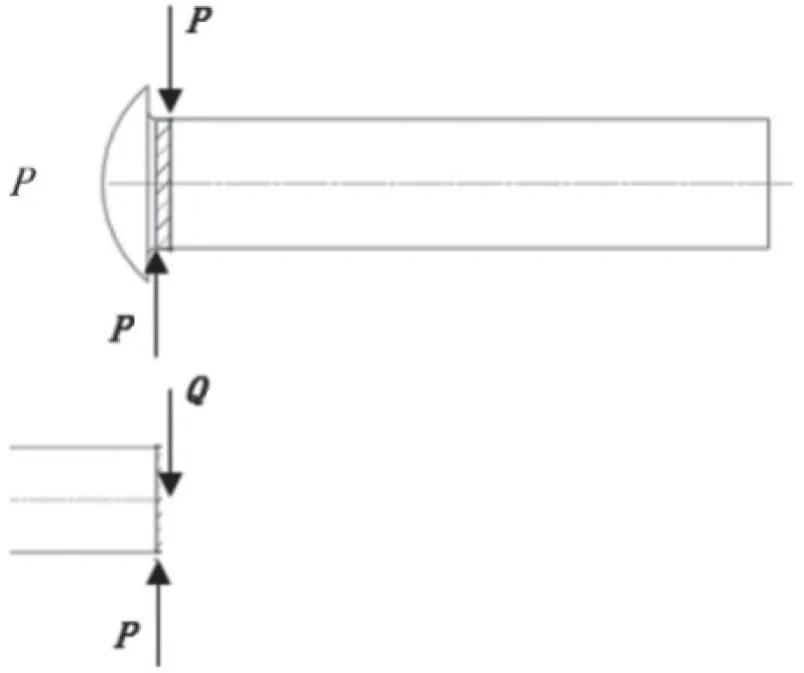
图7 铆钉剪切力

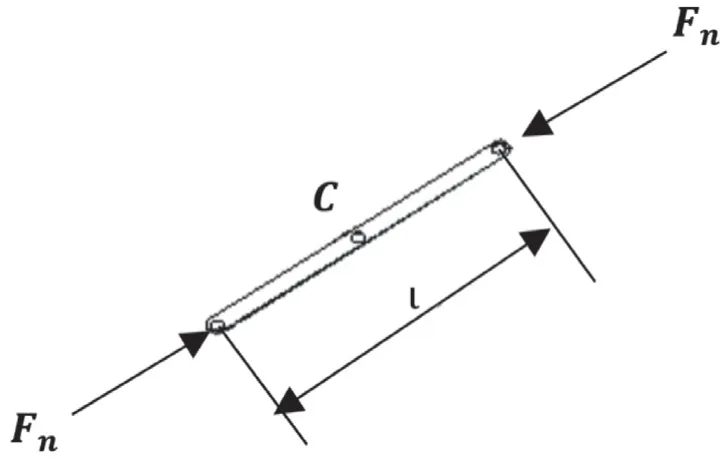
图8 单条折叠杆受力分析

根据约束条件：托架最大斜度β ≤15 °，折叠片最小斜度α ≤110 °，利用Matlab 软件边界条件函数工具解得铆钉剪力函数Fn在最大值时，β=2.87 °，α=97.45 °。

从铆钉的受力情况来分析，认为其仅受到纯剪切应力的作用，折叠杆所使用为圆铆钉，设铆钉截面直径为d，则铆钉的剪切面的面积为：

式中：

A—铆钉剪切面的面积；

d—铆钉截面直径。

根据剪切应力计算公式：

式中：

τ—铆钉剪切面所受到的剪应力；

Q—铆钉剪切面所受到的剪切力；

A—铆钉剪切面的面积。

铆钉在n 点所受到的剪力：

将公式（6）取0 得：

将公式（18）代入公式（19）得：

式中：

τn—铆钉所受到的剪应力；

d—铆钉截面直径。

F1—托架和晾杆自身的重力；

F2—挂于托架左端的衣物重力；

11—托架主体长度；

l—折叠片长度。

α—折叠片倾斜角度；

β—托架倾斜角度。

根据材料力学理论，判断材料正常工作容许采用的最高应力，一般都按以下公式来确定[11]：

式中：

[σ]—材料的许用拉应力；

σs—材料的屈服强度；

ns—安全系数。

铆钉的材质采用12Cr17Mn6Ni5N 不锈钢【SUS201】，[σ]为许用拉应力，[σ]=σs/n，n 为安全系数取1.7，σs取值275 MPa[12]。计算出：

将代入即

代入表1 参数，计算得：

F2＜551.29 N

为了使铆钉不受折叠片剪力失效，施加于托架单边的不平衡力应小于551.29。

1.2.3 折叠杆受力公式推导

从折叠杆的受力分析可知，当托架受到单边不平衡力时，单条折叠杆两头受挤压力而产生形变位移，从而导致折叠杆塑性变形失稳。

取单条折叠片进行受力分析，根据欧拉公式，折叠片失稳临界力Fcr[13]：

式中：

Fcr—折叠片的失稳临界力；

E—折叠片的抗弯刚度;

I—折叠片的惯性矩；

l—折叠片的长度。

折叠片的临界应力：

式中：

бcr—折叠片失稳的临界应力；

Fcr—折叠片的失稳临界力；

A—折叠片的截面积。

设折叠片的厚度及折叠片厚度和宽度分别为a，b，则折叠片的惯性矩：

式中：

I—折叠片的惯性矩；

a—折叠片的厚度；

b—折叠片的宽度。

折叠片失稳临界力：

为确保折叠片稳定，折叠片所受压力 Fn应小于临界压力Fcr，即：

Fn＜Fcr

代入公式（14）与公式（26），得到：

公式变换得到：

式中：

F1—托架和晾杆自身的重力；

F2—挂于托架左端的衣物重力；

l1—托架主体长度；

l—折叠片长度。

α—折叠片倾斜角度；

β—托架倾斜角度。

E—折叠片抗弯刚度;

a—折叠片的厚度；

b—折叠片的宽度。

折叠杆采用Q235 材料，通过查表得[14]，Q235 抗弯刚度E=200 GPa，安全系数ns取1.7，代入表1参数运算得：

F2＜790.9

1.3 失效模式对比分析

综上计算结果

1）考虑钢丝绳断裂失效模式，施加于托架单边的不平衡力：

F2(绳)＜582.84 N

2）考虑折叠杆铆钉受剪力失效，施加于托架单边的不平衡力：

F2(铆)＜551.39 N

3）考虑折叠杆受挤压力失稳失效，施加于托架单边的不平衡力：

F2(杆)＜790.9 N

对比：

由式（30）可知，随着施加于托架单边的不平衡力逐步增大，最先出现的失效模式为铆钉受剪力失效，然后出现钢丝绳断裂失效，最后出现折叠杆受挤压力失稳失效。

1.4 托架设计可靠性提升方案

综上计算分析结论，提升托架设计可靠性提升，应首先提高折叠杆铆钉的抗剪强度，铆钉受剪力公式为：

式中：

τn—铆钉所受到的剪应力；

d—铆钉的截面直径。

F1—托架和晾杆自身的重力；

F2—挂于托架左端的衣物重力；

l1—托架主体长度；

l—折叠片长度。

α—折叠片倾斜角度；

β—托架倾斜角度。

因折叠片长度，托架长度受到晾衣机实际使用条件制约，调整空间不大。由上述公式可知，在负载不变的情况下，加大铆钉的直径，可大大提高铆钉的抗剪强度，进而提升托架的设计强度。

提高钢丝绳的破断拉力，也是提升托架设计可靠性的重要手段，参考国标GB 8918-2006《重要用途钢丝绳》[10]，选用大直径钢丝绳，提升钢丝绳的材质，均为提高钢丝绳破断拉力的有效方法。

提升折叠杆的受压稳定性也是提高托架的设计可靠性的必要条件，折叠杆的失稳临界力公式：

式中：

Fcr—折叠片失稳临界力；

E—折叠片抗弯刚度;

a—折叠片的厚度；

b—折叠片的宽度；

l—折叠片长度。

由上公式可知，提高折叠杆的宽度和厚度和减少折叠杆的长度，均可有效提高折叠杆的耐受压力。因折叠片的宽度和长度受到晾衣机实际使用条件制约，提高折叠杆稳定性最有效的方案为提高折叠片的厚度。当然，选用抗弯刚度E 更高的材料，也可提高折叠杆稳定性，但考虑到经济性和提升幅度，选用抗弯刚度E 更高的材料为次优方案。

2 托架的经济性最优设计

因晾衣机有额定承重要求，实际使用中施加于托架的力不可能无限增大，本篇以市场上主流额定承载45 kg的晾衣机为例，根据前面建立的力学模型，反推出钢丝绳，铆钉，折叠杆的理论设计最小值，以供后期设计参考。

2.1 初始条件

假设挂于晾衣机的负载为45 kg，且按最极限状态，45 kg 负载全部挂于一侧晾杆，因单台晾衣机托架为两个，故单个托架单边所受力：

2.2 钢丝绳受载计算

将F2=220.5 N 代入公式（33）：

代入表1 参数求得 F0=694.9 N，钢丝绳需承载质量：

查表2 钢丝绳规格选用表得，7*7 规格，直径1.2 mm 钢丝绳最大承载质量为122.4 kg。故钢丝绳理论最低规格可选用7*7，直径1.2 mm。

2.3 铆钉受载计算

将F2=220.5 N 代入公式（23）：

τ0=129 MPa，代入表1 参数，求得：

d＞3.59 mm

由计算可得，铆钉的最小规格，可选用φ4 规格。

2.4 折叠杆受载计算

将F2=220.5 N 代入公式（29）：

代入表1 参数，求得：

a＞2.1 mm

由计算可得，折叠片最小厚度可选用2.1 mm。

2.5 对比总结

因晾衣机有耐用性要求（一般为使用运行寿命大于6 000 次）[15]，考虑到长期运行中钢丝绳磨损，铆钉，折叠杆受应力冲击产生金属疲劳，金属长期暴露在外受环境腐蚀等因素[16]，实际使用选型应比理论最小值高一等级，以确保晾衣机在长期使用中的可靠性。依据以上的分析计算，推荐3 个关键零件选型见表3。

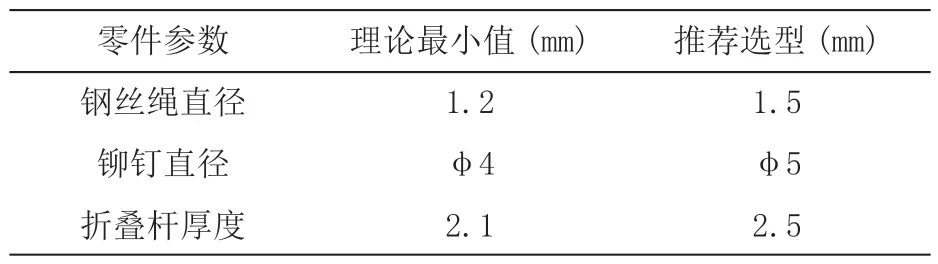
表3 各零件理论与推荐选用规格对比

3 结束语

本文通过对晾衣机托架折叠结构进行理论力学建模，研究晾衣机负载工作时，托架组件的受力和运动情况，推导托架上易损零件钢丝绳，铆钉，折叠杆的受力方程。分析托架在承受单边不平衡负载的情况下，各个部件的拉伸、剪切、弯曲等不同状况，并借助matlab 软件结合强度理论计算出各种失效模式下托架所承受的单边极限负载值，通过对比单边极限负载值，得出各种失效模式的发生顺序，分析发生原因，提出解决托架失效的措施，为托架设计的可靠性安全性提升提供理论指导。

根据前面所建立的负载及失效的理论模型，通过晾衣机额定负载值的约束，结合材料力学相关理论，反推出各零件的理论设计最小值，为托架设计的经济性提供理论指导，为企业创造客观的效益。