构建微专题,让复习更高效
2023-09-06祁胜林
祁胜林
摘要:在“双减”政策的背景下,教师只有实施精准化教学,才能实现减负高效提质的目标.而精准化教学的组织方式多种多样,其中微专题教学是值得推崇的一种教学方法.尤其是在学期末的总复习阶段,实施微专题复习模式,会使复习更有针对性、更易于操作,效率也会更高.
关键词:微主题;中点;辅助线;复习
1背景分析
进入八年级,学生的学习进入了关键时期.尤其是数学学科,与七年级阶段的基础性内容偏多相比,八年级是整个初中阶段学习难度提升较大的一年.具体体现在要求学生掌握的知识点增多,尤其是几何部分中性质定理的抽象性、几何图形的复杂多变性,对学生分析和解决问题的能力、抽象概括能力、逻辑推理能力、证明和表达的能力提出了更高的要求.因此,八年级是初中生学习的分水岭,一些能力较好的学生能迎难而上、攻克难关,而许多学生由于基础较薄弱,容易出现畏难情绪,数学成绩走下坡路.人教版八年级上册涉及的几何部分有《三角形》《全等三角形》《轴对称》,在期末复习阶段,这些内容涉及的概念、性质、定理以及应用是复习的重难点,当这些知识点糅合在一起对学生进行考查时,条件相对隐蔽和复杂,综合性强,灵活性大,往往需要教师拨开迷雾,指点迷津,辅之以总结方法,提炼思想.例如辅助线的作法和构造技巧,是这学期学生需要掌握的重难点,需要教师腾出较多的时间,给学生作专题复习.然而专题复习要求教师全面系统地归纳总结知識点和各类题型,提炼数学思想和方法,需花费大量时间准备,教学实施起来也需要大量时间和精力.为了在有限的时间里实现精准化教学,提高课堂教学的效率,不妨把这种专题细化成一个个微小专题,即现在提倡的微专题教学.
2构建微主题,实施高效复习策略
与传统的大专题复习相比,微专题复习的教学容量少,往往只是针对某一个知识点展开的,其讲授形式上可以多样化,时间上也不受限制,针对性强,易于操作,是一种精准化教学模式.从人教版八年级数学上册的几何部分的内容来看,有关辅助线的作法和构造技巧在内容上可以细分为中点的处理技巧、线段和差的处理技巧、角平分线问题的处理技巧、半角与倍角的处理技巧、一线三垂直模型的作法、利用等腰三角形“三线合一”的性质作辅助线的方法、构造全等三角形和等腰三角形的技巧.下面就以中点的处理技巧——与中点有关的辅助线作法为一个微专题,具体谈谈如何实施微专题教学.
2.1复习作法,确立微专题
在期末总复习阶段,教师首先需要帮助学生整合各章节的知识点,将平时学到的零散的、零碎的知识,尤其是一些有某种关联性的知识点,通过纵横比较、归纳与总结,有机地整合在一起,建立知识网络,形成结构体系.复习的过程,也是学生对之前学习的知识的重新认识和进一步深化和巩固,还可以帮助学生查漏补缺.
在教学实施中,教师可以通过提出问题:在这学期我们学习了哪些中点类问题呢?我们又是怎么处理这些问题的呢?帮助学生简单地回顾一些有关的知识点.从《三角形》章节中中线的概念和性质,到《全等三角形》章节中的遇到中线,如何作辅助线构造全等三角形,再到《轴对称》章节中的线段垂直平分线、等腰三角形、等边三角形,每一章里都涉及了中点、中线,整个学习过程从简单的三角形过渡到特殊三角形,在逐渐深入的探索和应用中,中线的性质也逐渐丰满起来.中线这一知识点无疑可以形成一个大板块的专题,而与中点有关的辅助线的作法是其中的一个细微又重要的专题,它是一种构图法,是基于中线的性质,再综合一些辅助线,构建基本图形的方法.大体上讲,可以归纳为四种方法.
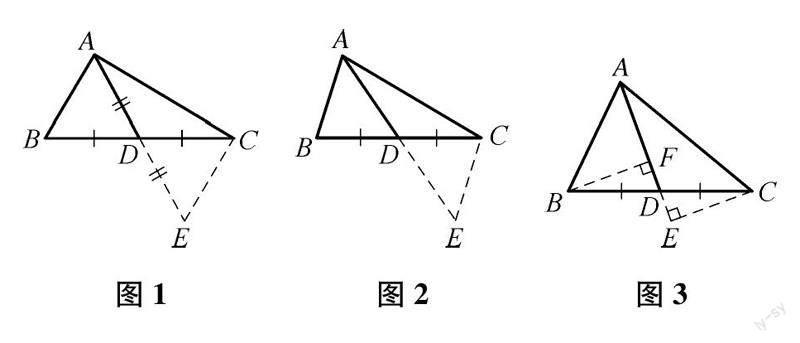
如图1-3,已知△ABC,D为BC的中点.
方法1:倍长中线法,如图1,延长中线AD,使DE=AD,连接CE,可得△ABD≌△ECD(SAS).
方法2:作平行线法,如图2,过点C作CE∥AB,交AD的延长线于E,可得△ABD≌△ECD(AAS).
方法3:作垂直法,如图3,过点B作BF⊥AD交AD于F,过点C作CE⊥AD交AD的延长线于E,可得△BDF≌△CDE(AAS).
这三种方法都能将题目条件转化到同一对三角形中来处理问题,可用于构造全等三角形、平行线、相等线段.
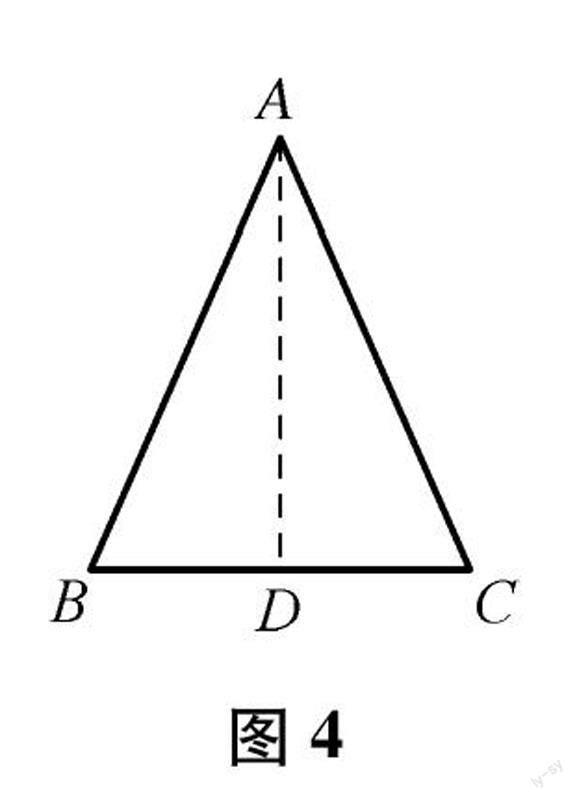
方法4:等腰三角形的“三线合一”法,如图4,已知等腰三角形ABC,且AB=AC.取底边BC的中点D,连接AD,则AD⊥BC,且AD平分∠BAC.
事实上,在△ABC中,① AB=AC;② AD平分∠BAC;③ BD=CD;④ AD⊥BC.对于以上四条语句,任意选择两个作为条件,都能推出另外两个结论,即“知二得二”.
2.2典例应用,巩固微专题
教师在选择例题时,可以先选择一些经典的、基础的、示范性的例题,若能将与中点有关的辅助线的多种作法用于解决同一题,实现一题多解,则可以帮助学生深入理解所学的知识.
例1如图5,在△ABC中,AD为中线,E为AB上一点,AD与CE交于F,且AE=EF,求证:AB=CF.
证法一:延长FD至G,使FD=DG,连接BG,如图6,
显然△BDG≌△CDF(SAS),∴∠G=∠CFD,CF=BG.
∵AE=EF,∴∠EAF=∠AFE.
∵∠AFE=∠CFD,∴∠EAF=∠G,
∴AB=BG,∴AB=CF.
证法二:如图7,延长AD至P,使AD=DP,连接CP.
显然△BDA≌△CDP,所以AB=CP,∠BAD=∠P,根据AE=EF,有∠EAF=∠AFE.又根据对顶角相等,故∠P=∠CFP.所以CP=CF,所以AB=CF.
证法三:过点B作BH∥CF,交AD的延长线于H,如图8,
显然△BDH≌△CDF(AAS),∴CF=BH.∠H=∠CFD.
∵AE=EF,∴∠EAF=∠AFE.∵∠AFE=∠CFD,∴∠EAF=∠H,∴AB=BH,∴AB=CF.
证法四:如图9,过点C作CQ∥AB交AD的延长线于Q.显然△BDA≌△CDQ,所以可得∠BAD=∠Q,AB=QC,根据AE=EF,有∠EAF=∠AFE.又根据对顶角相等,故∠Q=∠CFQ.所以CQ=CF,所以AB=CF.
证法五:如图10,过点B作BM⊥AD于M,过点C作CN⊥AD,交AD的延长线于N.
显然△BDM≌△CDN(AAS),∴BM=CN.
∵AE=EF,∴∠BAM=∠AFE.又∵∠AFE=∠CFN,
∴∠BAM=∠CFN.再证△BAM≌△CFN(AAS).
∴AB=CF.
这是一道典型的与中点有关的题目,证法一和证法二都运用了倍长中线法.由于存在中点,则必有一组边相等和中点处的对顶角相等,将中线或部分中线延长一倍,通过证明全等,从而实现相等线段和相等角转化的目的.证法三和证法四运用了作平行线法,由于有中点存在,则有一组边相等和中点处的对顶角相等,通过作平行,可得另一对角相等,根据“ASA”或“AAS”证明全等,为解决问题打开思路并提供必备条件.证法五则是运用了作垂直法.同样由于中点的存在,有一组边相等和中点位置的一对对顶角相等,通过作垂直,也可构造全等三角形继而解决问题.
将与中点有关的辅助线的三种作法灵活巧妙地运用于同一道题的解决中,体现了题目不在多而在精的原则,有利于学生比较这三种方法的区别和联系,进一步巩固所学的知识,在一题多解中打开思路,提高学习热情,体会数学解题的妙处.
2.3变式探究,深化微专题
变式探究题涉及的知识点多,综合性强,难度颇大,需要对已知条件的多方位挖掘,对几何图形的直观把握,对作辅助线的方法和技巧的熟练运用,这要求学生有较高的分析和综合运用所学知识解决问题的能力.
例2如图11,△ABC为等腰直角三角形,CA=CB,∠ACB=90°,M,N为直线BC上两点,BN=CM.连接AM,过C作CD⊥AM交直线AB于D,连接DN.
(1) 如图12,当M,N重合时,求证:∠AMC=∠DNB.
(2) 当M,N不重合时,(1)中结论还成立吗?试说明理由.
(3) 如图14,当M,N分别在BC,CB的延长线上时,作图并直接写出∠AMC与 ∠DNB之间的数量关系.
解析:(1) 作CF⊥AB于F,交AM于G,如图10,根据等腰直角三角形的“三线合一”的性质得到∠ACF=∠BCF=45°.因为CD⊥AM,所以∠1+∠ACD=∠2+∠ACD=90°,根据余角的性质得到∠1=∠2,推出△AGC≌△CDB(ASA),于是得到CG=BD,证得△CGM≌△BDN(SAS),所以∠AMC=∠DNB.
(2) 结论还成立.作CF⊥AB于F,交AM于G,如图15,同理(1),可以推出△AGC≌△CDB(ASA),于是得到CG=BD,再证得△CGM≌△BDN(SAS),根据全等三角形的性质即可得到结论.
(3) 如图16,过点C作CF⊥AB交AM的延长线于G,由CH⊥AM,得到∠GHC=∠GFB=90°,由于∠GCH=∠FCD,得到∠G=∠CDB,根据邻补角的性质得到∠ACG=∠CBD=135°,推出△ACG≌△CBD(AAS),得到BD=CG.证得∠MCG=∠NBD=45°,又由已知的BN=CM,推出△CGM≌△NBD(SAS).于是得到∠GMC=∠N,由于∠AMC+∠GMC=180°,等量代换得到∠AMC+∠DNB=180°.
例3已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,AB=AC,AD=AE,连接BE,CD,O是BE的中点,连接AO.
(1) 特例探究:如图17,当点D,E分别在AB,AC上时,线段AO与CD的数量关系是________,位置关系是________.
(2) 深入探究:如图18,当点D,E不在AB,AC上时,试判断(1)中的两个结论是否成立,若成立,请证明你的结论;若不成立,请说明理由(仅就图② 的情形).
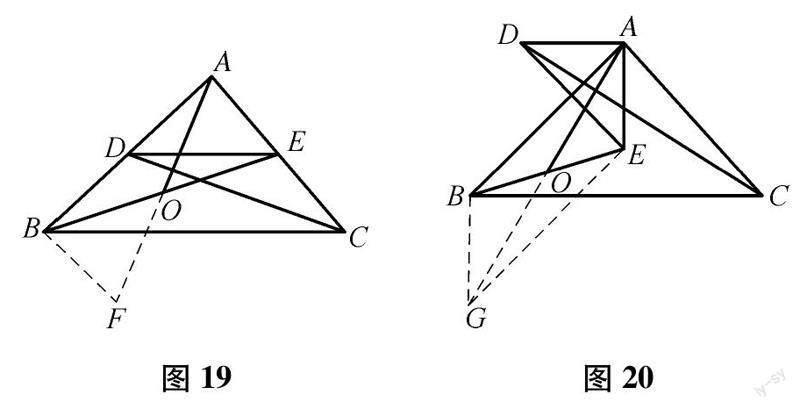
解析:(1) 由已知条件,先证明△DAC≌△EAB(SAS),所以CD=BE,∠ACD=∠ABE.再过点B作BF∥AE交AD的延长线于F,如图19,可得到△AOE≌△FOB(AAS),所以AE=FB,∠OAC=∠F,继而证得△ABE≌△BAF(SAS),所以AF=BE,所以AO=1/2AF=12BE=1/2CD,即AO=OE=OB,所以∠OAE=∠OEA=∠ADC.又∠DAO+∠OAE=90°,所以∠DAO+∠ADC=90°,所以AO⊥CD.
(2) 如图20,延长AO到G,使OG=AO,连接BG,EG.显然可以得到△AOE≌△GOB(SAS),所以AO=GO,AE=GB,∠OAE=∠BGO,所以AE∥BG,所以∠ABG+∠BAE=180°.又∠DAE+∠BAC=180°,即∠DAC+∠BAE=180°,所以∠ABG=∠DAC.故可以得到△ABG≌△CAD(SAS),所以AG=DC,所以AO=1/2CD.因为∠BAG+∠CAG=90°,所以∠ACD+∠CAG=90°,所以AO⊥CD.
例2是对等腰三角形“三线合一”法的综合应用,例3是以等腰直角三角形为背景的对中点辅助线的作法——作平行线法和倍長中线法的应用.两道题都是先从特殊情况着手,再过渡到一般情形的探究,虽然已知条件和图形变得更加复杂、抽象,但是特殊情形的解答过程往往隐含着一般情形的解决方法,所以只要厘清题目的条件,抓住问题的本质,找寻解决问题的突破口,确定基本的解题思路,解决问题也是水到渠成的.
像这种变式探究的综合题,作对辅助线是解决问题的突破口,一般来说需要借助辅助线巧妙地构造出全等三角形.有时会出现多根辅助线,和多次证明全等三角形的情况,这需要解题者步步为营,可以从待求的结论出发,采用逆向思维来推理,为含有结论的两个全等三角形找对应相等的边角关系.总之,基本的思路可以概括为从“未知”看“需知”,逐步靠拢“已知”.
3关于微主题复习的教学思考
以提升能力为目标的微专题复习是对重难点知识和重点题型的集中突破,是专题复习的进一步深化,是实现从学生已经掌握的知识或思想方法向实际解题能力转化的重要手段.
微主题的内容需要教师基于教情、学情、考情有针对性地选取材料,可以是教学的重点、难点,学生的易错点、易混点、疑问点,考试的高频知识点、易错点.这个“点”是建立在学生已具备初步的知识和能力的基础上的,它的切口要小,以便于在课堂有限的时间内进行具体地实施.
习题的讲解是实施微专题的关键环节,要以学生最近的能力生长点为落脚点,解法的依据是教材中要求掌握的知识点和基本数学思想方法,是学生必须具备的解题方法和技巧,切忌搞偏题怪题以及古怪的解法,否则就失去了微专题的构建意义.如果说知识点是微专题复习的圆心,那么习题是微专题复习的圆环.题目的讲解过程要呈现一个“圆形”的路径,从最基本的知识点出发,经过对题目的一系列分析和求解之后,再回过头来指导学生反思这些基本的知识点是如何应用于解题的.
微专题复习中引导学生进行思考,进行深度学习,把知识目标转化为能力目标,让学生有积极的情感体验,是教师的重要任务.教师除了需要在教学内容的呈现上要多加琢磨外,教学方式方法和教学评价上也要仔细研究.复习最忌一味地灌输式的讲解,其过程是可以丰富多彩的,如多媒体的介入,小组之间的合作与交流,讲练结合都可以让复习过程更有趣.
总之,微专题复习是一个系统的过程,从教学目标到内容设计,再到具体实施过程,都是需要教师精心准备和预设的.也只有这种有针对性、灵活性的微专题复习,才能提高复习的效率,提升学生的能力,培养学生的学科素养.参考文献:
[1] 杨小丽.初中几何概念教学的有效策略——以“线段中点”为例[J].数学通报,2021,60(9):3336.
[2] 史宁中.数学基本思想18讲[M].北京:北京师范大学出版社,2016.
[3] 史宁中.义务教育数学课程标准解读[M].北京:北京师范大学出版社,2012.
[4] 顧大权.数学教学中“微专题”复习的开展与运用[J].教学与管理,2018(31):5658.
[5] 李宽珍.“微专题”引领高效数学复习的思考[J].教学与管理,2015(28):6164.
