基于模糊概率法的土石方工程爆破开挖方案优选
2023-09-06吴建兵刘金鑫雷进生
吴 超,吴建兵,周 珂,刘金鑫,雷进生
(1.浙江华东工程咨询有限公司,杭州 311122;2.三峡大学 土木与建筑学院,宜昌 443002)
土石方开挖为水利、市政、房建等工程项目建设中常见的工作内容,也是项目建设全生命周期的重要一环。考虑各项目土石方工程的特点,筛选并构建土石方开挖工程影响因子论域,优选出合适的土石方工程开挖方案是确保土石方工程顺利开展的前提,对于整个工程项目的顺利完成具有重要意义。
土石方开挖有诸多种方法,常见的有人工开挖、机械开挖、工程爆破开挖、CO2致裂开挖等[1]。其中工程爆破作为一门古老而又新颖的技术学科,直接服务于国民经济建设的多个领域[2-4]。如卢文波[5]以三峡工程临时船闸及升船机岩体爆破开挖为依托,对与围岩爆破损伤影响范围有关的岩石基础开挖中的合理爆破方式与程序选择、岩质高边坡及中隔墩的爆破振动控制等几个与爆破开挖相关的主要问题作了概括性的介绍;基于LS-DYNA二次开发的累积损伤仿真技术,胡英国等[6]对光面爆破和预裂爆破2种不同爆破方式下的开挖损伤分布特征进行了全过程数值仿真,并对比了两者的不同;以实验为基础,费鸿禄等[7]利用数值分析软件ANSYS/LS-DYNA对3种方案的爆破振动下在役管线的影响规律进行了研究,选出了管沟爆破开挖的最优方案;罗笙等[8]对锦屏二级水电站辅助洞爆破开挖的损伤进行了研究,给出了一种基于法向冲击荷载的爆破损伤模拟法。
本文针对白鹤滩迁建集镇土石方工程开挖量大、开挖条件复杂、工期短等特点,结合AHP法及模糊概率基本原理[9],在充分考虑影响因子权重的复杂性、不确定性及模糊性等自身故有特性的基础上,对人工开挖、机械开挖、爆破开挖与CO2致裂4种土石方开挖方法进行评价,工程爆破开挖评选结果为最优。为此设计4种工程爆破方案,将3种主要的工程爆破灾害及总成本共4种影响因子作为方案的评选因子进行土石方爆破施工方案的优选,以期为类似土石方工程爆破开挖方案的优选及工程应用提供参考。
1 模糊概率模型评选步骤
事件发生的程度即为模糊,事件发生与否的不确定性即为随机,事件随机出现的统计规律称为概率[10-12]。许多事件往往模糊性与随机性并存,此类问题的研究是将2种不确定性结合起来考虑,这即为模糊概率可以解决的问题[13]。模糊概率基本原理中的模糊权重能够覆盖传统确定性方法所涉及的权重取值范围,更具科学合理性,具体论述可参见文献[14]。
模糊概率模型评选的主要步骤如下:
(1) 根据工程实际,建立方案的论域A={a1,a2,…,am}及影响因子的论域B={b1,b2,…,bn};
(2) 对影响因子bi进行单因素评价,选择合适的隶属函数aj(bi),即确定了aj是论域B上的一个模糊子集。进而求出两个论域间的模糊关系矩阵R
(1)
式中:aj(bi)表示第i个影响因子对应的第j个方案的隶属度;模糊关系矩阵R=(rji)m×n,其中rji=aj(bi)。
(3) 确定影响因子bi的模糊权重(即把模糊权重看做模糊数)πi(i=1,2,…,n)
(2)
式中:λi,0为相对权重;系数βi,1…βi,2k的值可从0.5、0.6、0.7、0.8、0.9中合理挑选;可参照λi,0对λi,1…λi,2k进行合理取值。
(4) 利用模糊语言概率公式对模糊事件的各评选方案aj的概率进行计算
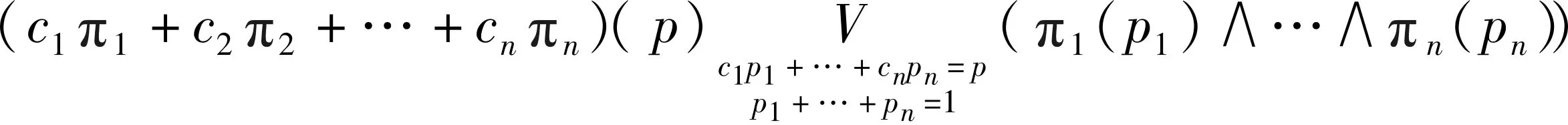
(3)
p(aj)=aj(b1)π1+aj(b2)π2+…+aj(bn)πn
(4)
式中:πi为第i个方案影响因子的模糊权重;pi为相应论域{λi,1,…,λi,k,λi,0,λi,k+1,…,λi,2k}上的任意取值;p(aj)为评选方案aj的模糊概率;ci为评选方案的第i个隶属度,对于第j个评选方案ci=aj(bi),算子∨为“取平均”,∧表示“取小”。
(5)
(6)
(7)
2 土石方开挖方法的评价
2.1 工程概况
白鹤滩水电站会东县迁建集镇移民工程溜姑营盘山场平工区,地处金沙江左岸。西面有一处276人永久性不拆迁民房,结构为土墙,距离最近开挖点约190 m,工区面积约为0.28 km2,土石方开挖量约为622万m3。
受到白鹤滩水电站下闸制约,土石方开挖要求工期为1 a且不可延长。受到各种不利因素制约,运输平均强度大,且高峰施工运输强度持续时间长,因此开挖方法的筛选对施工效率的影响是十分关键的。在保障安全的前提下,提升施工进度,是本工程面临的重大难题之一。
依托本工程所遇到的上述问题,为寻求可行的技术方案,组织专家开展复杂条件下的大体量高强度开挖技术方案的研讨,以实现经济效益及社会效益的最大化。
2.2 AHP及模糊矩阵R的构造
通过对实际问题的研究分析,首先构造合理的综合评判递阶层次结构图,共3个层次,即目标层、准则层、方案层(图1)。
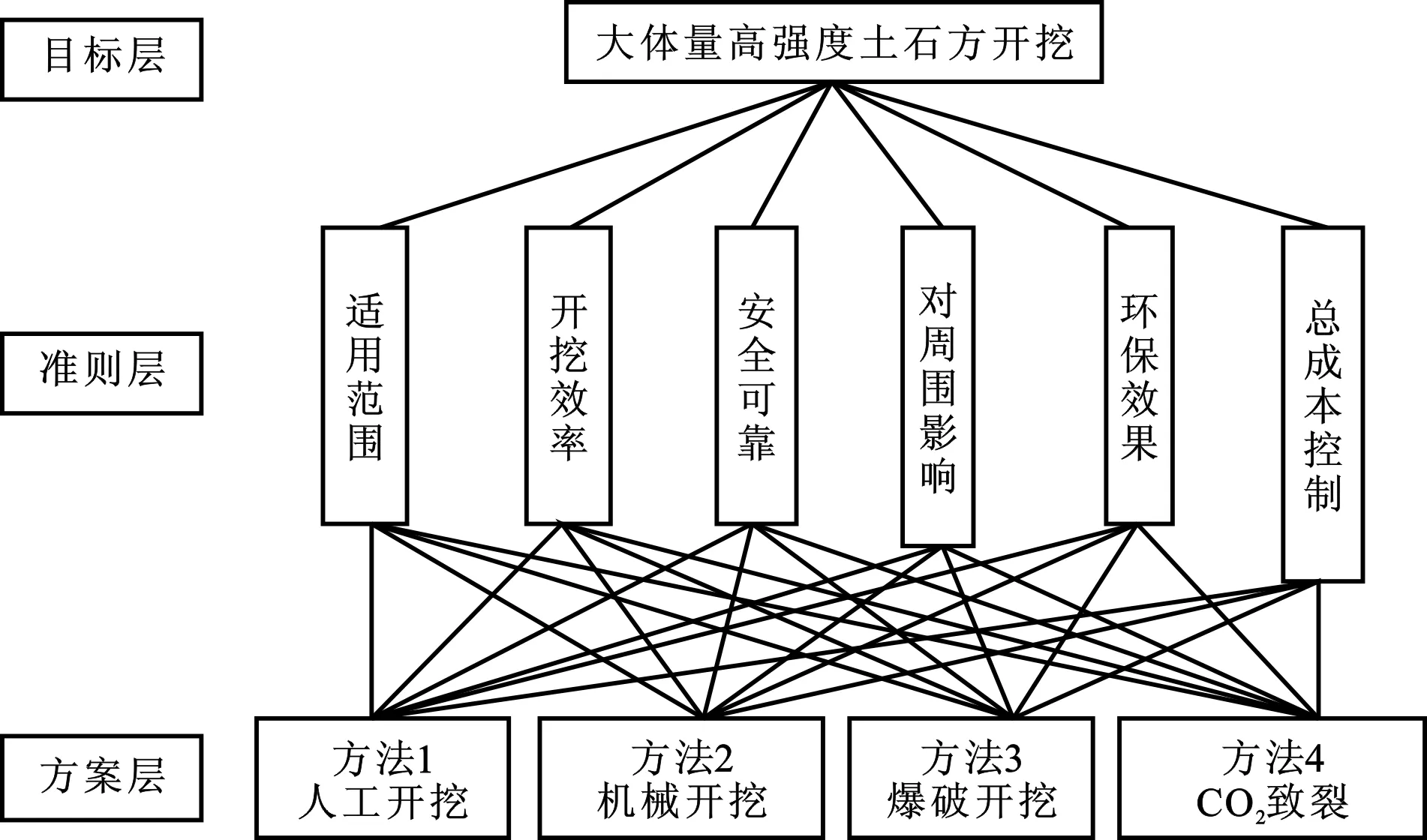
图1 土石方开挖方法评判递阶层次结构图Fig.1 Hierarchical structure diagram of earth-rock excavation method evaluation
影响土石方开挖的因子较多,各影响因子的影响程度也有大小轻重之分,结合工程实际的地质条件、工程特征等,经相关资料查阅及专家研讨,将首选的4种土石方开挖方法及筛选的6种影响因子运用模糊语言进行逻辑评判(表1),其中方法论域A={a1,a2,…,an},影响因子论域B={b1,b2,…,bm}。

表1 土石方开挖方法影响因子及逻辑评判Tab.1 Influence factor and logical evaluation of earth-rock excavation method
以上逻辑评判将逻辑评语划分为{很差,差,较差,一般,较好,好,很好}共7个等级,将逻辑评语等级一一对应集合{0.0,0.2,0.4,0.5,0.6,0.8,1.0}中的值,根据式(8)对逻辑评语等级进行模糊数的赋值
(8)
通过式(5)~式(7),对7个逻辑评判等级进行归一化处理,得:{0.024,0.057,0.110,0.143,0.176,0.228,0.262};结合表1,可得每个影响因子对于各个方法的对应隶属度,表示成矩阵形式即为模糊矩阵R。
2.3 模糊权重的计算
较为传统的相对权重计算方法有:Delphi法、特征向量法、最小平方和法、AHP法等[15]。本文首先运用专家调查1~9标度法及AHP法列出正反判断矩阵并进行相对权重的计算(表2),再运用模糊概率模型评选式(2)进行模糊权重的计算。

表2 正反判断矩阵的构造Tab.2 Construction of positive reciprocal judgment matrix
对表2中的正反判断矩阵进行一致性校核,得:λmax=6.150,CI=0.030,RI=1.24,CR=0.024<0.1,表明校核结果符合预期。运用MATLAB对6种土石方开挖方法影响因子的相对权重λi,0进行计算,可得
λi,0=[0.176,0.382,0.106,0.041,0.061,0.234]
6种土石方开挖影响因子的模糊权重可根据式(9)进行计算,式中系数λi,j和βi,j的取值可参见表3及表4。

表3 系数λi,j的取值Tab.3 Values of coefficientλi,j

表4 系数βi,j的取值Tab.4 Values of coefficient βi,j
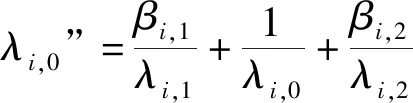
(9)
以上影响因子的模糊权重计算充分考量了权重的模糊、不确定等概率特性,权重的可信赖程度大幅提升。根据式(3)~式(7)对土石方开挖的4种方法的评判值进行计算,可得:(0.093,0.230,0.369,0.308),可见,在选取的6种影响因子条件下,工程爆破开挖评选结果为最优。
3 工程爆破方案的优选
3.1 爆破开挖方案
考虑到工程爆破方案的选择对开挖效果同样具有较大的影响,工程施工中设计了4种爆破开挖方案[5-7]:(1)梅花布孔。采用倾斜钻孔形式,钻孔深度控制在2~5 m,进行耦合装药,使用反向塑料导爆管雷管进行排间顺序微差起爆,排间时差△t控制在30 s左右;(2)方形布孔。各排孔依次向着前排爆破出现的临空面,钻孔深度控制在2~5 m,采取分段间隔不耦合装药,且各孔洞放入多发同规格塑料导爆管雷管,并进行多排孔梯形微差起爆,排间时差△t控制在30 s左右;(3)预软化爆破方法PSBM(Pre-Softening Blasting Method)。在较难爆破的土石方工区先行布孔,预先进行爆破。在其内部发生松动后再次进行全面钻孔爆破。后期钻孔形式为倾斜多排方孔,进行耦合装药,使用反向塑料导爆管雷管进行排间顺序微差起爆;(4)综合爆破方法CBM(Comprehensive Blasting Method)。考虑到方案2及方案3中分段间隔不耦合装药及预软化爆破的可能优势,在较难爆破工区先进行不耦合装药并先行起爆;后采用倾斜多排方形布孔,进行分段间隔不耦合装药,并进行多排孔梯形微差起爆,起爆各孔依次向着前排爆破出现的临空面,且各孔洞放入多发同规格塑料导爆管雷管。
3.2 AHP及模糊矩阵R的构造
同理,根据专家调查1~9标度法及AHP法,从所设计的4种工程爆破方案中筛选出4种工程爆破的主要影响因子,进而进行工程爆破方案评判递阶层次结构图的构造及影响因子的逻辑评判,分别见图2和表5。

表5 工程爆破方案影响因子及逻辑评判Tab.5 Influence factor and logical evaluation of project blasting scheme
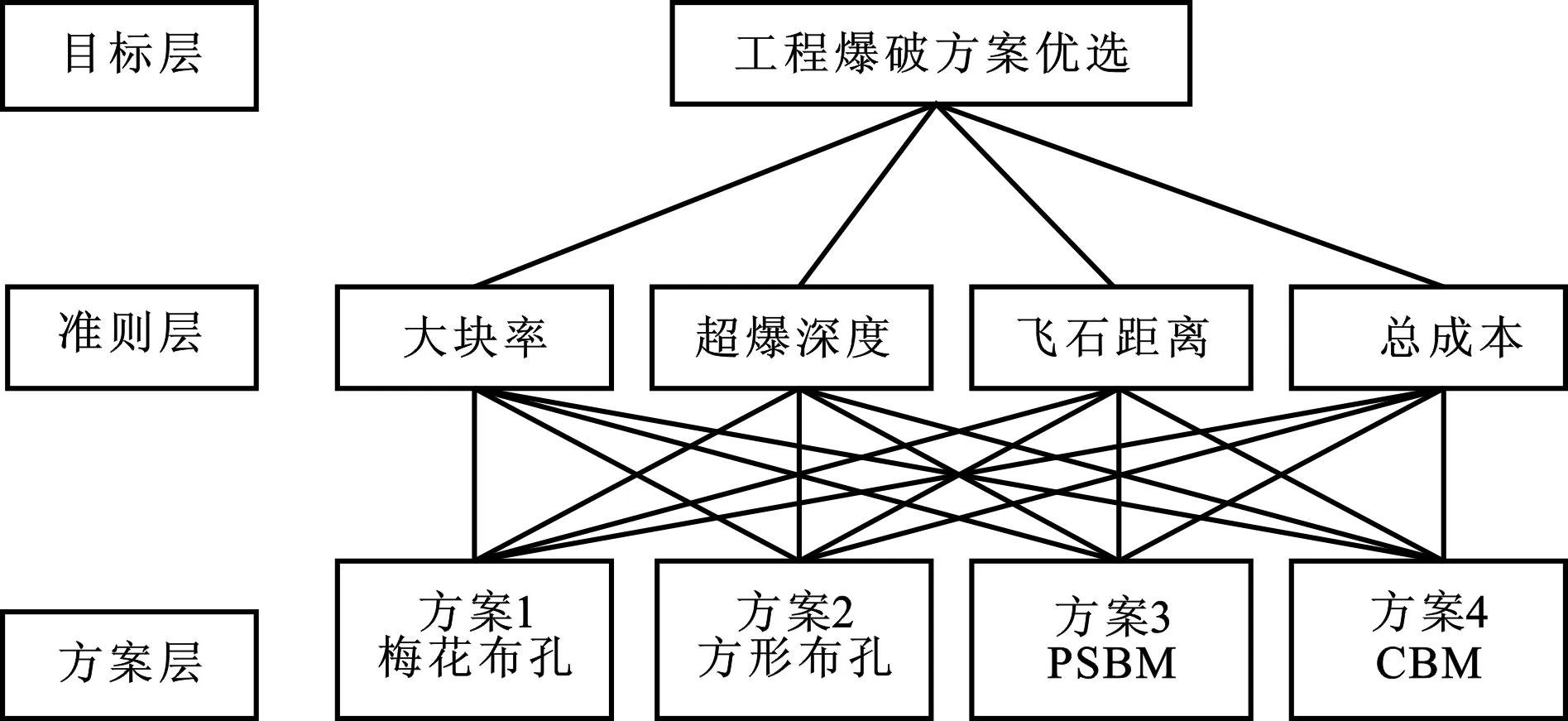
图2 工程爆破方案评判递阶层次结构图Fig.2 Hierarchical structure diagram of engineering blasting scheme evaluation
根据式(8),对逻辑评语的等级划分进行模糊数的赋值。同理可得工程爆破4种影响因子隶属度取值组成的模糊矩阵R
3.3 模糊权重的计算
表6中给出了4种影响因子的正反判断矩阵,对其进行一致性校核,可得:λmax=4.071,CI=0.024,RI=0.9,CR=0.026<0.1。表明一致性符合预期。

表6 正反判断矩阵的构造Tab.6 Construction of positive reciprocal judgment matrix
经MATLAB计算,可得4种工程爆破影响因子的相对权重为
λi,0=[0.293,0.185,0.415,0.107]
根据式(9)对模糊权重进行计算,系数λi,j和βi,j的取值可参见表7及表8。最后由式(3)~式(7)计算可得,4种工程爆破方案的评判值依次为(0.214,0.205,0.283,0.298),即:方案4优于其他3种方案。

表7 系数λi,j的取值Tab.7 Values of coefficient λi,j

表8 系数βi,j的取值Tab.8 Values of coefficient βi,j
4 结论
(1)针对土石方工程中开挖方案优选问题,考虑影响因子权重的复杂性、不确定性及模糊性,基于模糊概率法原理,结合工程实际的地质条件、工程特征,将开挖方法及影响因子运用模糊语言进行逻辑评判,可以很好地优选出满足工程实际要求的土石方开挖方案;(2)考虑土石方工程爆破开挖方案的选择对开挖效果的影响作用,从设计的4种工程爆破方案中筛选出4种工程爆破的主要影响因子,计算出对应的模糊权重进行逻辑评判,结果表明,综合爆破方案优于其他爆破方案;(3)研究可为类似土石方工程爆破开挖方案的优选及工程应用提供参考。
