基于IAFSA-SVM的岸电电源IGBT电气故障诊断
2023-09-06李伟昊吴佳彬崔广开王冠妍王郭靖岳晓丰
李伟昊,吴佳彬,崔广开,王冠妍,张 晨,王郭靖,岳晓丰
(1.天津水运工程勘察设计院有限公司,天津 300456;2.天津东方泰瑞科技有限公司,天津 300192)
随着中国经济的快速发展,能源消耗问题和环境污染问题日益加剧。船舶在港口停泊期间,采用柴油发电机进行发电所产生的污染物是造成空气污染的主要原因之一[1],同时还产生了较大的资源浪费。为强化船舶大气污染物排放控制,落实船舶靠港使用岸电要求,2018年12月,交通运输部印发《交通运输部关于印发船舶大气污染物排放控制区实施方案的通知》,《通知》对须使用岸电的船舶进行了具体说明。因此,船舶岸电技术以接入港口陆地电网取代停泊期间的柴油发电机发电的方法,逐渐成为解决能源消耗问题和环境污染问题的主要途径。目前,我国拥有许多港口岸电码头,然而大部分远洋船舶负载用电频率为60 Hz,与我国陆地电网的供电频率50 Hz不符,因此陆地电源不能够直接为停泊船舶供电[2]。船舶用电的特殊性也对岸电电源的电能质量提出了更高的要求,变频电源作为岸电系统核心部件,其运行的可靠性决定了岸电系统的稳定性。
岸电变频电源由移相整流变压器、功率单元、输出滤波器和控制部分组成,其控制为电压外环电流内环的双闭环控制模式。绝缘栅双极性晶体管(Insulated Gate Bipolar Transistor,IGBT)是变频电源内部核心元器件之一,以其为主的驱动电路位于主电路和控制电路之间,在变频电源内部担任非常重要的角色[3]。IGBT不仅具有高可靠性、驱动简单、易保护、开关频率高的特点且无需缓冲电路。通常情况下,可通过开发高电压、大电流、频率高的高压IGBT来获得不同频率的电流[4]。但由于变频系统的功率器件为电力电子元件,其特性较其他设备软,短时过压过载能力比较脆弱,对工作环境要求较高,故出现故障后具有排除故障时间长、修复费用高等特点。因此,利用人工智能技术,对IGBT故障的类型、机理特征及影响因素进行分析,寻找故障原因与特征参数之间的内在规律,运用大数据及人工智能进行类比、分析,对可能产生的IGBT故障进行前期预测,并采取相应的技术措施,能够极大提升岸电使用的稳定性和运行的经济性,对于岸电系统的正常使用以及安全性的提升有着重要意义。目前关于岸电系统逆变器故障诊断的研究较少,但其主要组成与普通逆变器相似,可以利用相关的理论方法来研究和讨论岸电电源逆变器的故障诊断[5]。IGBT故障诊断方法主要是基于人工智能算法对电流、电压信号的分析。PENG等[6]提出了一种基于有限控制集模型预测控制(FCS-MPC)识别单个开路开关故障的故障诊断方法,其采用矩阵变换器(MC)拓扑的时间离散模型和成本函数来选择下一个采样周期的最佳开关状态,并通过监测负载电流和判断开关状态来定位故障开关实现IGBT故障诊断。WANG等[7]基于核熵分量分析理论,结合极限学习机分类算法,探讨了应用名为KECA-ELM的集成方法处理超级降压转换器电路(SCC)中的硬故障和软故障诊断的可行性。ZHOU等[8]提出了一种基于正常和故障条件下电容器电压的相似性分析的子模块电压相似性、实时、快速的模块化多电平转换器(MMC)开路故障检测和定位(FDL)方法,实验结果验证了所提出的方法可以在一个基本周期内快速准确地检测和定位开路故障。
本文提出了一种改进的人工鱼群算法(Improved Artificial Fish Swarm Algorithm,IAFSA)结合支持向量机(SVM)的故障诊断算法,通过短时傅立叶变换(Short-Time Fourier Transform,STFT)的变频器输出电流的功率谱密度(PSD)特征为输入特征,将IAFSA引入,作为SVM的参数优化算法。IAFSA将步长修正因子和全局随机行为作为改进方法引入到人工鱼群算法(Artificial Fish Swarm Algorithm,AFSA)当中的鱼群步长来提高全局搜索和局部搜索的性能,提出基于该改进方法的IAFSA,并构建IGBT故障诊断模型,为IGBT故障诊断提供一种新的可能性。
1 岸电变频电源供电方式及指标
目前,基于变频电源的岸电供电方式主要分为“一对一”和“一对多”供电[9]。本文研究基于“一对一”供电方式,即一艘船舶停靠期间的用电只由一个变频电源所供应。在该供电方式下,码头变电站相互独立,其中一个或多个故障并不会影响其他变电站。
目前,船舶岸电配电电压等级分为低压和高压2种,低压岸电电源输出为440 V/60 Hz、400 V/50 Hz,高压岸电电源输出为6.6 kV/60 Hz、6 kV/50 Hz,本文所提及的岸电变频电源以岸电高压上船式为例(图1),其中陆地输出高压为10 kV/50 Hz的电源作为岸电系统的输入,主电路由功率单元串联构成多电平变频电源,其控制部分采用电压外环电流内环的双闭环控制模式,最终输入到船舶用电系统中为6.6 kV/60 Hz高压交流电,其中逆变单元的系统拓扑结构如图2所示。此外,根据JTS155—2012《码头船舶岸电设施建设技术规范》中所规定的岸电供电系统标准,变频电源性能指标峰值时间Tp、调节时间Ts以及超调量Mp须分别满足0.4 s、1.5 s和5%的要求。

图1 典型岸电电源供电系统结构Fig.1 The typical shore power supply system structure

图2 变频电源逆变单元拓扑结构Fig.2 The inverter unit topology of variable frequency power supply
2 基于SVM的诊断模型
2.1 支持向量机(SVM)
支持向量机(SVM)是一种二分类模型。它的基本模型是一个线性分类器,在特征空间上定义了最大边距,最大边距将其与感知器区分开来。支持向量机的学习策略是最大化边距,对于做出标记的两组向量,给出一个最优分割超曲面把这两组向量分割到两边,使得两组向量中离此超平面最近的向量(即所谓支持向量)到此超平面的距离都尽可能远,可以形式化为求解凸二次规划的问题,也等价于最小化正则化铰链损失函数的问题[10]。
SVM还包含内核函数,这使得它可以成为一个非线性分类器。在处理线性不可分问题时通过将核函数映射到更高维度的空间中进行线性可分来解决。其中,高斯核函数、多项式核函数、径向基核函数(RBF)等核函数是SVM常用的核函数[11]。本文采用具有较好的泛化能力以及快速学习收敛能力的RBF函数作为最终选择的核函数。在IGBT故障诊断模型中,构建非线性SVM分类器需要确定两个主要参数:惩罚因子c以及核函数参数g。
2.2 人工鱼群算法(AFSA)
在自然界中,鱼能够自行寻找或尾随其他鱼寻找食物,即鱼群聚集地即为生存所需要的物质存在最多的地方。人工鱼群算法就是根据这一行为,通过构建人工鱼群模仿鱼群聚集(即鱼为保证生存和躲避危害而产生的聚集,遵循分隔、对准、内聚规则)、追尾(即当鱼群中的一条或者几条鱼发现食物时,其相近的鱼会迅速向其聚拢)以及觅食(即鱼在水域中自由移动,一旦发现食物则迅速游往食物点)等生存行为来实现参数寻优的仿生智能算法[12]。AFSA实现步骤如下:
(1)初始化基础参数,包括鱼群规模(N)、每条鱼的初始位置、视野(Visual)、步长(Step)、鱼群的拥挤度(δ)以及寻优次数(Trynumber);
(2)计算鱼群中每个个体的适应值,并选取其中最优值赋值给公告牌;
(3)对鱼群各个体进行评分,选取需要执行的生存行为,包括聚集、追尾、觅食以及评分行为;
(4)执行(3)所选择行为,更新自身,生成新的鱼群;
(5)对鱼群所有个体进行评分,若其中个体评分优于公告牌,则公告牌数值更新为该个体数值;
(6)当公告牌最优解达到设定阈值或完成循环次数,迭代终止,否则继续跳转至步骤(3)进行循环。
2.3 改进的人工鱼群算法(IAFSA)
传统的AFSA中人工鱼的步长被设定为一个固定值,过小的步长则会造成收敛缓慢的问题,更容易陷入局部最优,并导致寻优时间过长优化成本增加等问题;但是如果设置较大的人工鱼步长,则在寻优过程中很容易跳过所要寻找的最优值,也会导致寻优失败,参数优化时间变长等问题。为解决这一问题,本文采用自适应变步长来改进AFSA,通过该方法,在同一个循环中,增加离更优解距离较远的人工鱼的步长,以加速收敛过程;降低距离较近的人工鱼的步长,同样提高了收敛速度。本文在IAFSA中引入修正因子β,定义如下
(1)
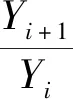
Visuali+1=Visuali×β
(2)
Step=a×Visual
(3)
式中:a为视野步长系数(0 此外,为防止寻优过程陷入局部最优,本文引入了全局随机行为来解决这一问题,即引入公告板机制,若公告板中最优值在循环一定次数之后的变化范围仍然小于设定阈值ε,考虑其陷入了局部最优,将鱼群中最差评分的指定个数的个体实行全局随机行为,以式(4)实行 xi+1=xi+α×Visual×rand() (4) 式中:α为设定值,其值越大越容易脱离局部最优,计算量也随之增加。 经过IAFSA来选取SVM的最优参数,构建IGBT故障诊断模型,以得到最优分类结果,图3为模型流程图。 图3 IGBT故障诊断流程图Fig.3 The flow chart of IGBT fault diagnosis 为验证IAFSA的有效性,选择了3个测试函数与AFSA进行对比[13],AFSA和IAFSA初始参数设置如表1所示。 表1 AFSA和IAFSA初始参数Tab.1 The initial parameters of AFSA and IAFSA 测试函数f1(x1,x2),f2(x1,x2),f3(x1,x2)定义如式(5)~式(7)所示,其中-4≤xi≤4。 (5) (6) f3(x1,x2)=-[x12-10cos(2πx1)+x22-10cos(2πx2)]-20 (7) f1(x1,x2)在定义域内只有一个极值点,求取该极值即为该函数最优解,在(0,0)处取得最小值为-1;f2(x1,x2)在定义域内有无数个极值点,但只有一个最大值,求取最大值即为该函数最优解,但容易陷入局部最优点即局部极值点,在(0,0)处取得最大值为1;f3(x1,x2)在定义域内求取最大值即为该函数最优解,但由于其复杂多峰的函数特性,同样容易陷入局部最优点即局部极值点,在(0,0)处取得最大值0。图4、图5和图6分别为AFSA和IAFSA在三个函数上的求解最优解的过程,结果表明,IAFSA在求解过程中表现出了更好的收敛速度和性能,能够在较少的迭代次数中得到最优解,并且能够很好地解决局部最优的问题。 图4 对f1(x)的求最优解过程Fig.4 The process of finding the optimal solution for f1(x) 图5 对f2(x)的求最优解过程Fig.5 The process of finding the optimal solution for f2(x) 图6 对f3(x)的求最优解过程Fig.6 The process of finding the optimal solution for f3(x) 实验以拓扑结构中的一组6个IGBT构成变频电源逆变单元的受控通断为例,通过MATLAB进行仿真,变频电源仿真模型图如图7所示。对变频器中的6个IGBT进行编号,分别为VT1、VT2、VT3、VT4、VT5、VT6,对应单管故障命名为F1、F2、F3、F4、F5、F6。经研究发现,IGBT故障发生时,大多数情况只有最多2个IGBT发生故障。此外,由于逆变单元在同一相上的两个IGBT同时发生故障时就已损坏[14],因此在本文中排除这种情况。经过组合,得到18种故障类型如表2所示。 表2 故障类型及对应标签Tab.2 The fault type and the corresponding labels 图7 变频电源仿真模型图Fig.7 The variable frequency power supply simulation model diagram 本文对18种故障类型分别进行仿真得到12组数据,共216组数据样本。对每种故障类型选取其中的6组样本作为训练数据,剩余6组样本作为测试数据进行验证模型有效性实验。变频电源输出信号在故障时和正常状态下是不同的,在发生故障时输出在同一频带下具有不同的能量值,通过STFT对输出信号进行分析,并计算PSD分析不同频段的能量值来进行故障诊断。 在本文中,STFT采用窗长为256的海明窗进行分析,以避免频谱泄漏导致的幅度信息不准确的问题[15]。离散时间序列的STFT计算式如下 (8) (9) 由于经STFT后提取的特征数值较大,采用归一化对特征进一步处理,计算式如下 (10) 式中:y为最终的特征值;x为当前特征值;xmin和xmax分别为特征数据的最小值和最大值。 利用改进的人工鱼群算法选择SVM最优参数,将经特征提取之后的特征序列作为输入,实验样本被分为18类,得到分类结果。此外为验证IAFSA对于SVM参数优化在IGBT故障诊断中的有效性,本文还使用了随机参数、粒子群优化算法(PSO)和AFSA对SVM进行参数更新,完成了分类任务。PSO的初始种群大小设置为20,加速因子为c1=1.0,c2=1.6,迭代次数设置为100[16];AFSA的初始鱼群数量为30,迭代次数为100,拥挤度因子为0.5,最大寻优次数设置为15,初始步长为1,视野范围设置为1.5。IAFSA具体参数设置见表2。 随机参数和各算法下的基于SVM的IGBT故障诊断分类准确率如表3所示。 表3 各参数SVM分类准确率Tab.3 The accuracy of SVM with different parameters 通过验证结果进行可视化如图8所示,可以得出随机参数下的SVM虽然可能达到较好的分类性能,但不可避免的具有较差的泛化性,训练集测试集分类准确度相差较大。此外,基于IAFSA的SVM分类准确度明显优于PSO和AFSA算法下的SVM分类器,分类准确度达到了训练集100.00%和测试集90.93%。结果表明,IAFSA可以通过引入自适应变步长和全局随机行为来改进AFSA,进而对SVM参数进行优化,可以显著提高IGBT故障诊断模型的泛化能力和分类性能。 8-a 随机参数 8-b PSO算法 本文对IGBT的故障诊断进行研究,建立岸电变频电源的仿真模型,计算经过STFT变换的输出电流PSD作为诊断模型的特征。以此为基础,通过自适应变步长和全局随机行为构建IAFSA优化SVM参数,提高SVM的泛化性,在对18种故障数据样本分类时达到了90.93%的准确度,可以很好地识别岸电变频电源中IGBT的故障类型,以便进行后续维修。2.4 基于IAFSA的IGBT诊断模型
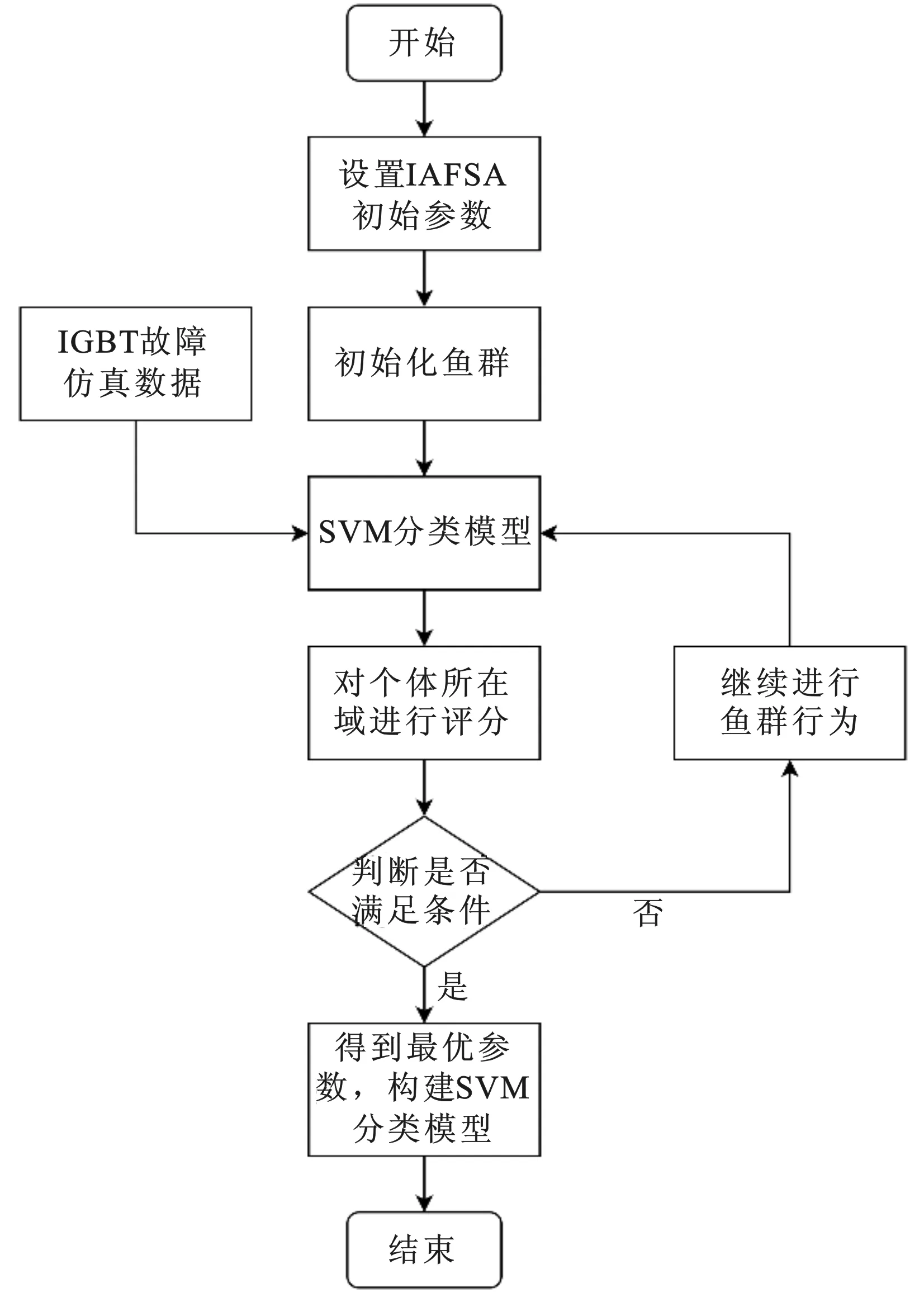
3 IAFSA算法验证
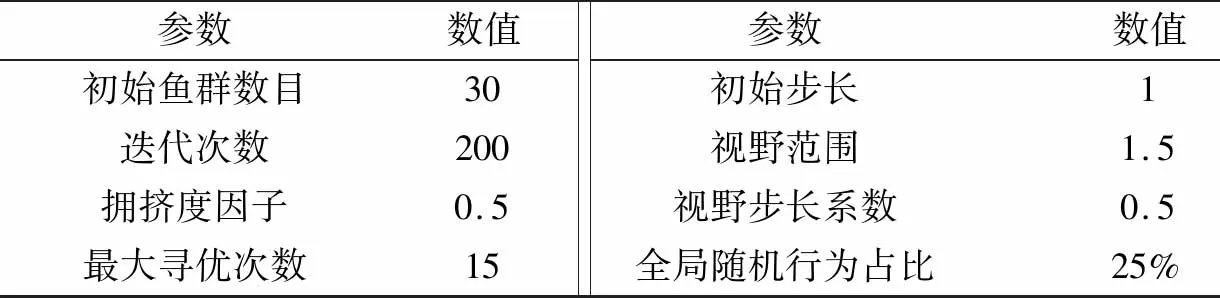
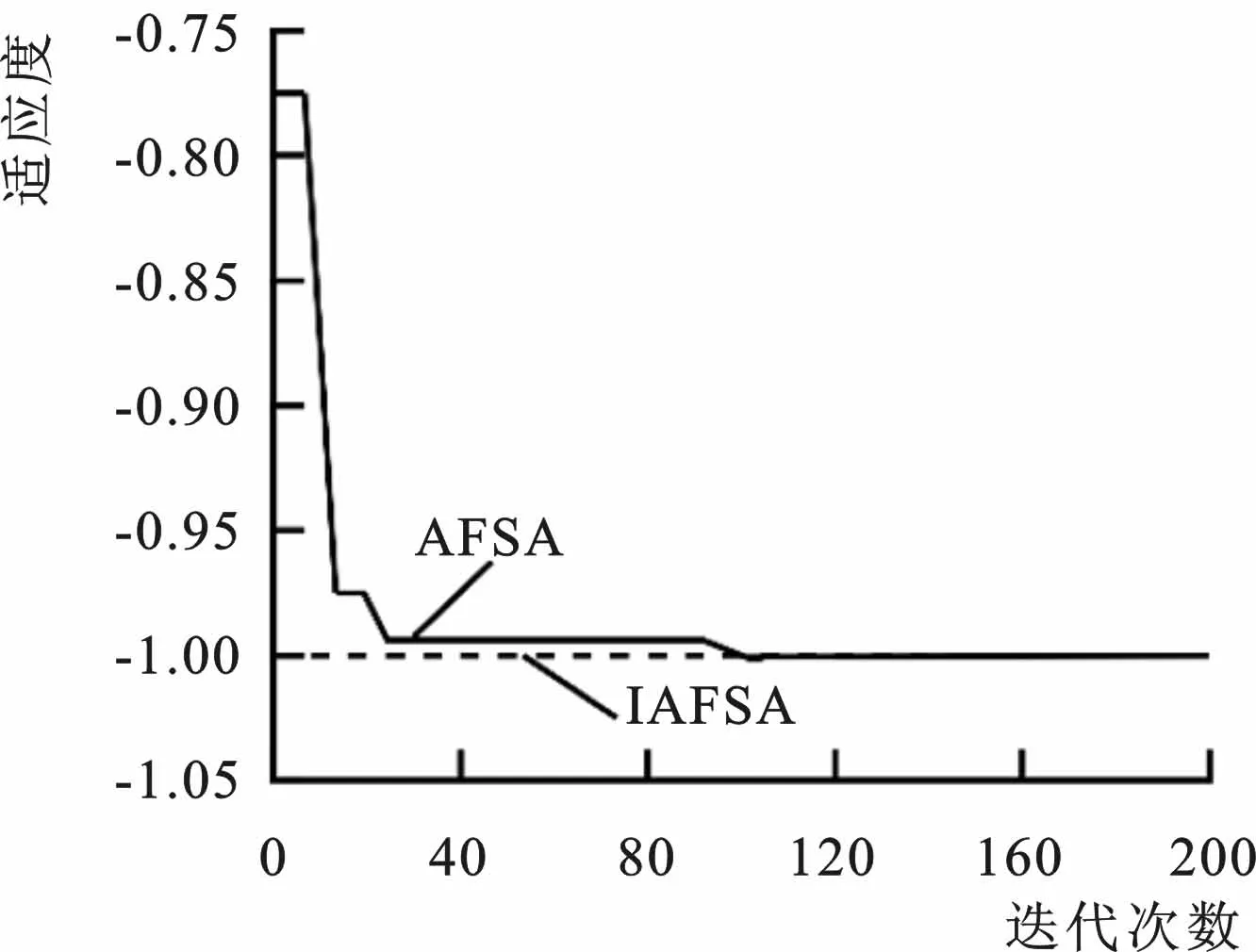

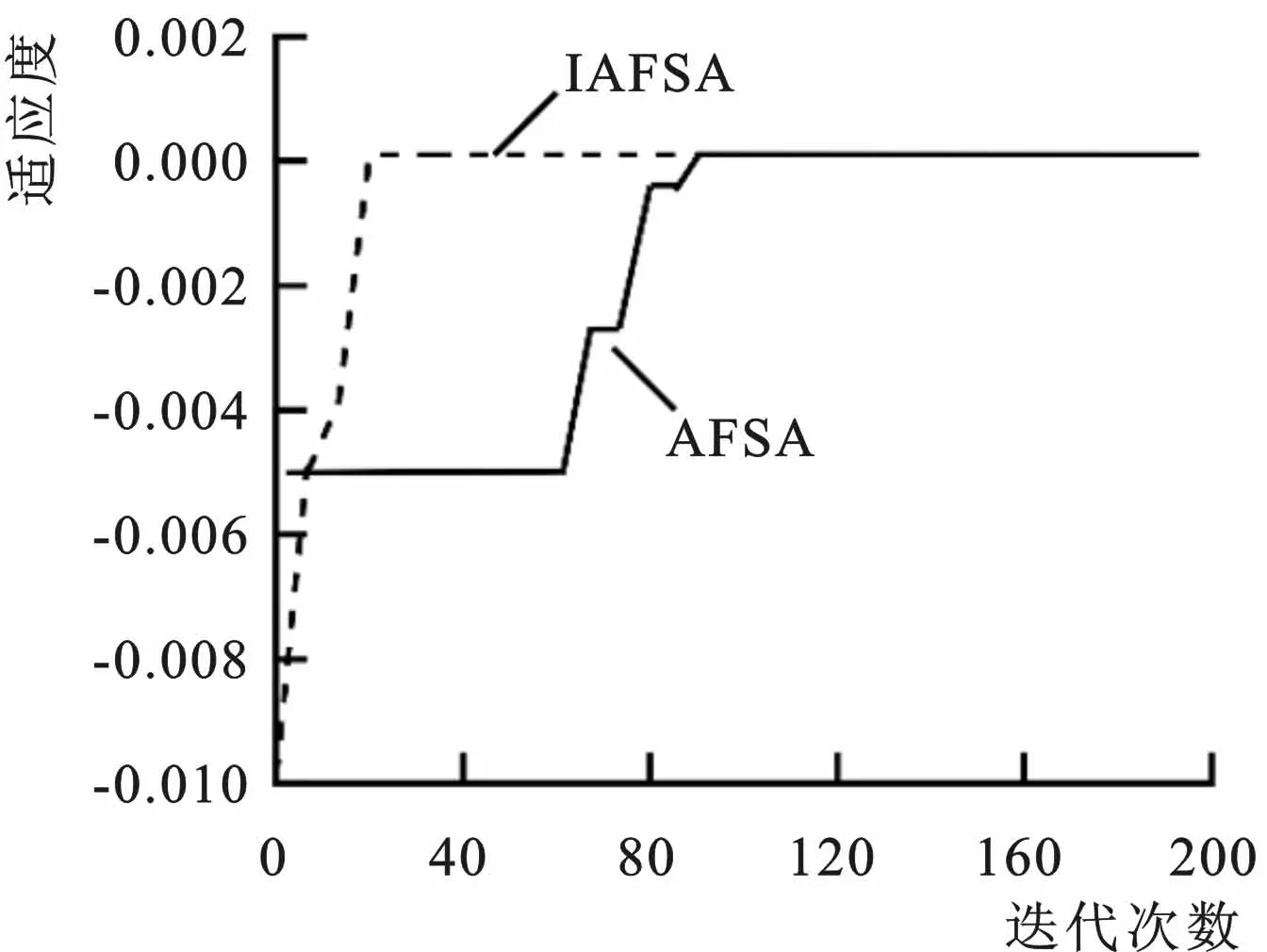
4 仿真
4.1 特征提取
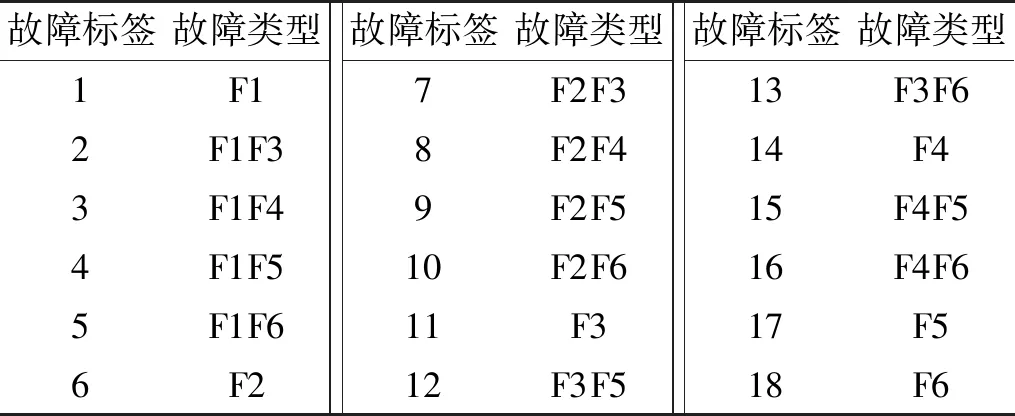


4.2 IGBT仿真故障诊断结果

4.3 结果分析

5 结论
