基于凸多边形粗骨料模型的混凝土氯离子扩散细观数值模拟

2023-09-06袁春坤王元战

水道港口 2023年3期

李伟,袁春坤,王栋,廖镜,王铎,王元战

(1.中国路桥工程有限责任公司,北京 100011;2.天津大学水利工程仿真与安全国家重点实验室,天津 300072)

海洋环境下,由于氯离子侵蚀诱发的混凝土内钢筋锈蚀是导致结构物发生耐久性失效破坏的主要因素之一,混凝土中氯离子传输扩散特性是钢筋混凝土耐久性研究的重要内容。目前,对混凝土中氯离子扩散的研究方法大多采取物理试验[1-4],但进行物理试验往往需要耗费较大的成本,且试验周期和试验条件有很大的局限性。随着计算机技术的发展,近年来一些学者采用更加高效、方便的数值模拟方法研究混凝土中氯离子的扩散特性[5-8]。数值模拟包括宏观概化模型和细观模型两种。宏观概化模型把混凝土看作一个均质的介质,不能考虑其内部骨料和界面过渡区的传输特性[9],这种宏观概化模型忽略了混凝土的复合材料特性,难以清晰地揭示混凝土内各相组成对氯离子扩散特性的影响。细观模型将混凝土考虑为由水泥砂浆、粗骨料及界面过渡区组成的三相非均质材料[10]。由于粗骨料的硬度和致密性较高,通常假设氯离子不在粗骨料中传输,但对氯离子传输存在曲折、稀释效应。界面过渡区由于含有较高的孔隙率,会加速氯离子的扩散[11]。因此,粗骨料及界面过渡区的随机生成及投放技术对混凝土内氯离子扩散细观数值模拟具有重要意义。

有关氯离子扩散细观数值模拟研究中,彭国军等[12]用有限元方法研究了二维八边形骨料体积分数对氯离子扩散的影响。DU等[13]建立了圆形、规则四边形、椭圆形粗骨料形状的二维细观有限元模型,分别探讨了粗骨料体积分数、水灰比等因素对混凝土中氯离子扩散的影响。LIU等[14]建立了二维多离子传输有限元模型,研究了界面过渡区、离子结合等在氯离子扩散中的作用。WANG等[15]采用三维球形细观模型进行混凝土氯离子扩散数值模拟,建立了海洋潮汐区环境下混凝土内氯离子长期扩散预测模型。此外,部分学者也提出了建立不规则形状粗骨料的细观数值模型。WITTMANN等[16]建立了具备一定随机程度的多边形骨料模型,但其形状与实际差别较大,且没有考虑界面过渡区的影响。ABBAS等[17]采用二维成像技术生成混凝土多边形粗骨料细观模型。高政国等[18]提出以圆为基础建立基骨料,并通过在最长边上随机延凸的方式建立随机凸多边形粗骨料模型。ZHENG等[19]基于随机游走算法,建立混凝土粗骨料模型,并研究了混凝土中氯离子的扩散特性。

目前,大多数学者在研究中都将粗骨料简化为圆形、正多边形等规则的几何形状,建立混凝土氯离子扩散细观数值模型。但实际上混凝土粗骨料多为碎石,其形状为随机多边形,采用规则形状的粗骨料模型进行数值模拟与实际工程存在较大差异。少数研究者建立的不规则形状骨料模型,其生成和投放效率较低,且没有考虑界面过渡区影响。针对上述问题,本文提出插点排序算法,考虑粗骨料位置和粒径分布的随机性与不重叠性,生成更接近实际形状的随机凸多边形粗骨料,建立了混凝土氯离子扩散的细观数值模型。相比于目前延凸算法生成的凸多边形粗骨料模型,本文建立的细观数值模拟方法具备更高的计算效率。通过物理试验数据,对本文建立的细观数值模型进行了验证。采用细观数值模拟方法,研究了粗骨料体积分数对混凝土内氯离子扩散规律的影响。

1 混凝土凸多边形随机骨料细观模型

首先建立符合实际骨料粒径大小、级配以及位置分布的砂浆-粗骨料-ITZ三相细观模型。设置混凝土为a×b的长方形单元,粗骨料体积分数fa定义为所有粗骨料与模拟单元的面积比。根据相关研究,碎石骨料的边数可设为4～12[20]。为了简化并确保最终模型具有显著的随机特征,假定凸多边形骨料边数n=12。

1.1 生成混凝土凸多边形随机粗骨料

基于富勒级配的粗骨料二维粒径累积频率分布可以用下式表示[21]

(1)

式中：F(d)为骨料粒径大于d的累积频率;d为骨料粒径;dmin为最小骨料粒径;dmax为最大骨料粒径。在粗骨料生成算法中,粗骨料粒径即为凸多边形的最小外接圆直径。

粒径分布服从F(d)的粗骨料生成算法如下：

(1)联合求解式(1)和式(2)得到di。

F(di)=ui1

(2)

式中：F(di)为粗骨料粒径小于di的累积频率;ui1为unifrd(0,1)函数生成的[0,1]区间的任意随机数。

(2)判断是否满足dmin≤di≤dmax,如果满足则进行下一步,否则重复步骤(1)直到满足条件。

(3)在直径为di的圆上任意选取3个点形成三角形。

(4)判断形成三角形是否为锐角三角形,如果不是则重复步骤(3)直至生成锐角三角形。

(5)存储三角形点和线的信息,并计算其面积si,并记录多边形边数初始值n=3。

(6)在圆内随机选取一个点作为凸多边形的一个新顶点;判断形成的新多边形是否为凸多边形;如果是,n=n+1进行下一步骤。

(7)记录每个顶点的坐标,并将新的三角形面积si,new添加到si中,即

si=si+si,new

(3)

(8)当n=12时,停止并将骨料的信息数据保存到单元格数组中。

这是一种新的生成具体凸多边形随机骨料的插值分类算法。重复此过程,直到总骨料含量大于设置的粗骨料体积分数,即停止循环。插值排序算法采用蒙特卡罗方法生成符合FULLER分级曲线的随机凸多边形集合。与传统的延凸算法相比,其算法简便且计算效率较高。

1.2 骨料的随机投放和ITZ生成

在投放过程中,应保证粗骨料随机分布在模拟单元内。根据相关试验结果[22],在混凝土表面层0.1 mm范围内为无粗骨料的纯砂浆层。因此,设置了0.1 mm的纯砂浆层。具体算法如下：

(1)将1.1节生成的粗骨料按粒径从大到小进行排序,后续投放也按此顺序进行。

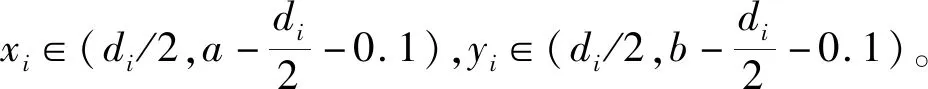
(3)判断骨料i和j( 1,2,…,i-1)骨料是否重叠。凸多边形粗骨料重叠的可能情况有3种,如图1所示。重叠判别的具体步骤如下：

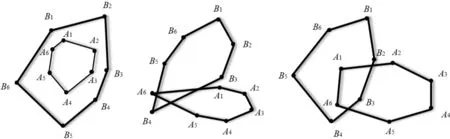
图1 凸多边形骨料可能的重叠情况Fig.1 Possible cases of overlapping convex polygon aggregates

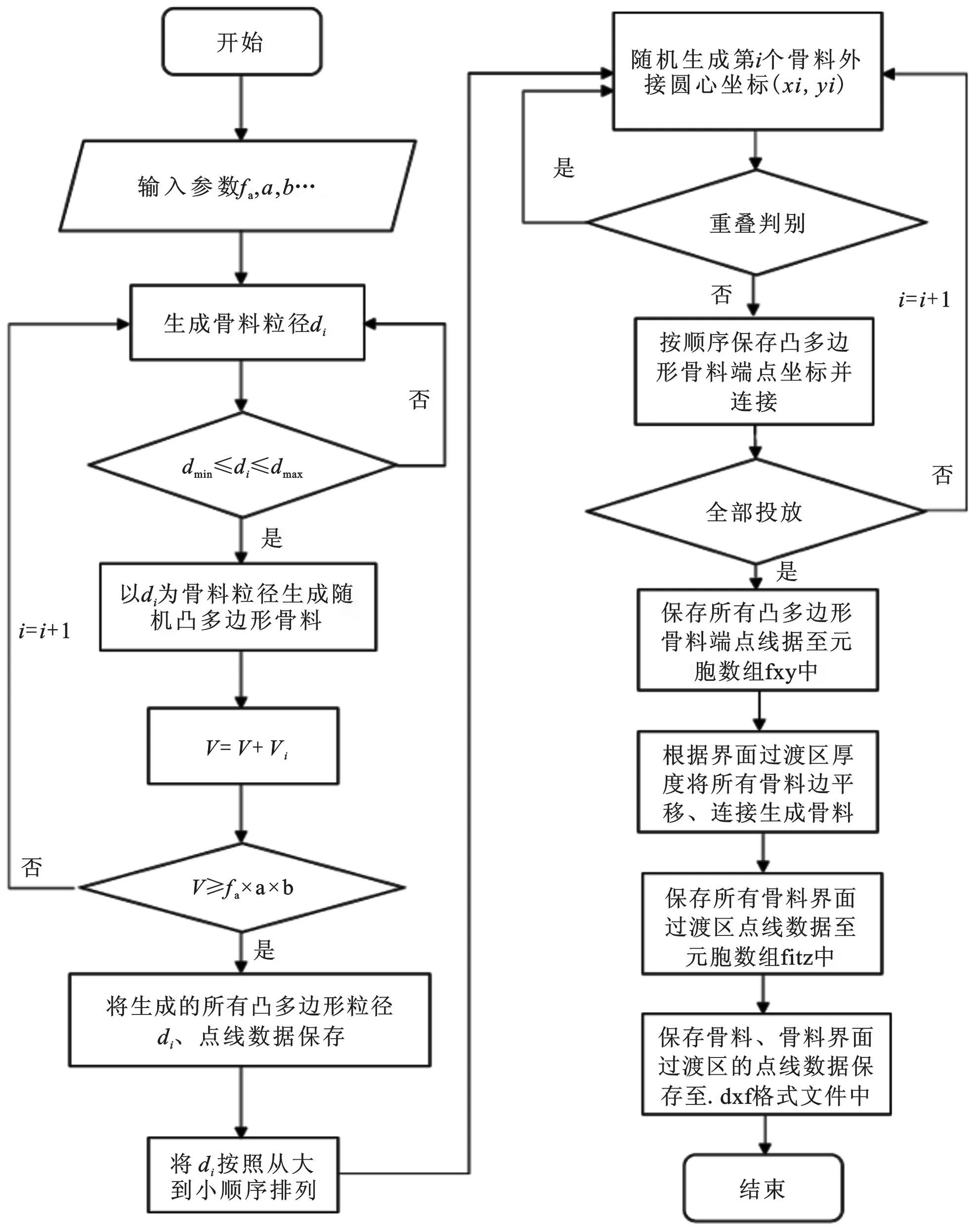
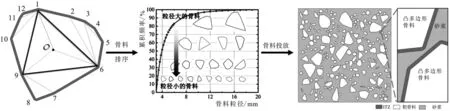
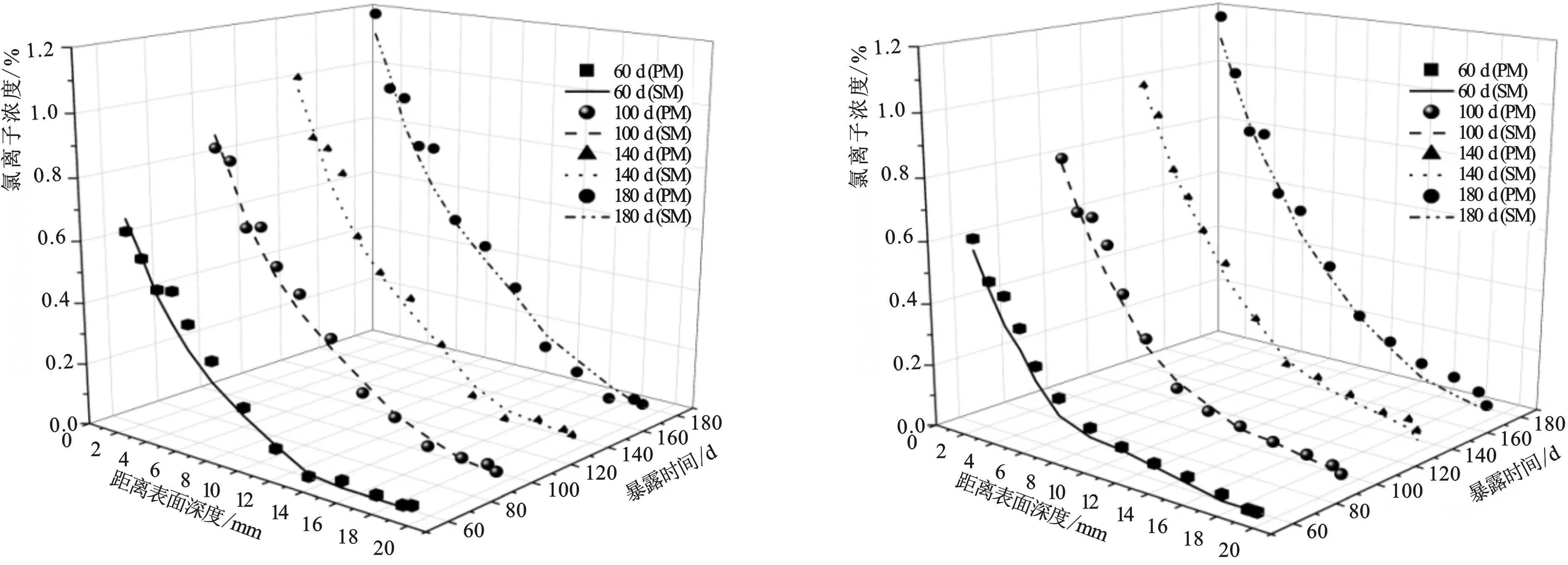
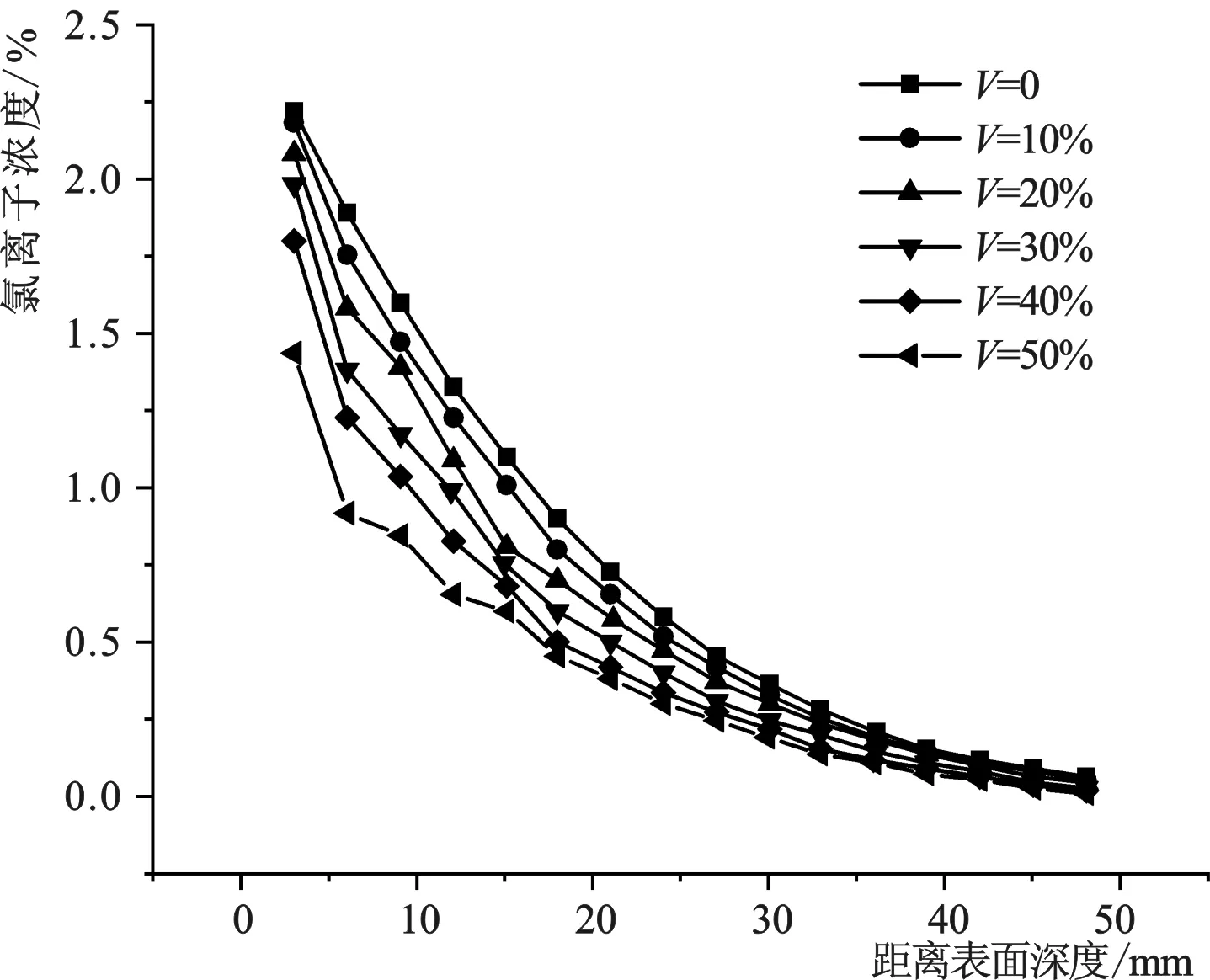
①判断第i个骨料的圆心和第j个骨料的圆心距离Lij是否大于两骨料的半径和,如果di/2+dj/2

②判断第i个骨料是否存在顶点在第j个骨料的内部。若存在,则重叠,返回步骤(2)重新生成骨料坐标;否则,继续进行下一步判断。

③判断第i个骨料和第j个骨料是否有交点。如有交点,则重叠,返回步骤(2)重新生成骨料坐标;若没有交点,则骨料不重叠,投放成功,继续进行第i+1个骨料的投放。

直至将所有生成的骨料全部投放完成后,在每个骨料周围生成固定厚度的界面过渡区[23](Interfacial Transition Zone,ITZ)。由于ITZ是质软的可重叠物质,因此ITZ之间无需进行重叠判断,也无需进行ITZ与粗骨料之间的重叠判断。

1.3 程序流程图

根据1.1节、1.2节,生成混凝土凸多边形随机骨料模型的程序流程图如图2所示。

图2 凸多边形随机骨料模型流程图Fig.2 Flow diagram of convex polygon random aggregate model

根据上述步骤,设置粗骨料体积分数为0.3,混凝土单元尺寸为100 mm×100 mm,粗骨料粒径范围为5～20 mm,生成的混凝土模型如图3所示。生成的骨料随机分布在混凝土结构单元中,级配合理,与实际混凝土截面类似,说明本文生成的随机模型具有正确性和合理性。

图3 骨料生成和投放过程Fig.3 Generation and distribution process

2 氯离子扩散细观数值模型验证

2.1 氯离子扩散试验

胶凝材料选用密度为3 100 kg/m3的PO.42.5型普通硅酸盐水泥,细骨料采用细度模数为2.7、表观密度为2 610 kg/m3的河砂,粗骨料采用表观密度为2 690 kg/m3的碎石。根据规范[24]制作尺寸为100 mm×100 mm×100 mm的正方体素混凝土试件。粗骨料体积分数分别为0、20%、30%、40%,粗骨料最大粒径为20 mm。混凝土试件配合比如表1所示。为保证氯离子传输只从单一表面扩散,除侵蚀面以外的其他5个表面均匀涂抹环氧树脂。

表1 混凝土配合比Tab.1 Mix proportion

试验采用人工海洋环境自动化模拟装置来模拟实际的潮汐循环过程[15]。试验前,配置3.5%的氯化钠溶液,将混凝土试件均匀放置在4个盛有氯化钠溶液的实验箱中。潮汐循环周期为24 h(12 h干燥、12 h湿润),循环次数为180次,分别在60 d、100 d、140 d、180 d时取出试件进行磨粉取样。将混凝土粉末通过0.63 mm筛子,筛余的粉末放置于温度为(105±5)℃的烘箱中烘干,2 h后取出放入干燥器冷却至室温。

选用CL-E型氯离子含量快速测定仪进行混凝土粉末的自由氯离子含量测定。在清洗干净的锥形瓶中放入样品粉末2 g,倒入60 mL的蒸馏水,用磁力搅拌器搅拌均匀,静止后取上层清液,将清洗好并用滤纸吸干的氯离子电极和参比电极同时插入上层清液中,测定自由氯离子含量。

2.2 模型验证

为了验证本文创建数值模型计算结果的合理性,基于物理试验模型确定相关参数进行数值模拟。根据试验数据确定的相关参数主要包括初始氯离子浓度、砂浆初始氯离子扩散系数、龄期系数、表面氯离子浓度。初始氯离子浓度由试验直接测得。氯离子扩散模型采用基于菲克第二定律的时变扩散模型[15]。不同龄期下的砂浆扩散系数通过纯砂浆试件在不同龄期下的氯离子浓度分布曲线拟合得到,再用砂浆扩散系数拟合Thomas时变公式[15]即可得到砂浆初始氯离子扩散系数和龄期系数。表面氯离子浓度也通过拟合过程得到。具体过程可见文献[15]。

基于上述物理试验的研究条件,分别建立相同尺寸、粗骨料体积分数下的混凝土凸多边形骨料随机细观模型。模型建立结果如图4所示。对不同粗骨料体积分数各10组混凝土试件分别进行数值模拟,数值模拟各项参数设置见表2。计算得到不同扩散时间下氯离子浓度沿深度的分布,取均值作为结果进行数据分析。

表2 数值模拟计算参数Tab.2 Numerical simulation calculation parameters

4-a V=20% 4-b V=30% 4-c V=40%图4 粗骨料体积分数分别为20%、30%、40%的混凝土细观模型Fig.4 The mesoscopic model of concrete with coarse aggregate of 20%,30%,40%

将不同骨料体积分数下数值模拟计算得到的氯离子浓度结果与物理试验结果进行对比,绘制三维对比图如图5所示。在图5中,SM为数值模拟计算结果,PM为物理模型试验结果。可以发现,数值模拟得到的氯离子浓度分布与物理试验得到的浓度分布趋势相同,误差在25%以内。在深度较大处,出现了数值模拟计算结果比物理试验结果偏高的情况,其原因可能是氯离子浓度测量仪器在浓度较低时灵敏度不足。综上所述,本文建立的混凝土随机模型通过数值计算得到的氯离子扩散结果与物理试验结果吻合良好,可靠度较高,验证了本文建立的混凝土细观模型进行氯离子扩散数值模拟的正确性和合理性。

5-a V=20% 5-b V=30%

3 粗骨料体积分数对氯离子扩散的影响

分别建立粗骨料体积分数为0(仅含砂浆)、10%、20%、30%、40%和50%的混凝土细观模型。初始条件、边界条件等参数设置同表2。利用本文建立的数值模拟方法,研究了粗骨料体积分数对混凝土中氯离子扩散特性的影响。暴露时间t=1 800 d时,粗骨料体积分数为30%的混凝土氯离子轨迹图如图6所示。

从图6可以看出,由于粗骨料的存在,氯离子集中在粗骨料前部,而在骨料后方氯离子浓度相对降低,进一步说明了粗骨料的存在会阻碍混凝土中氯离子传输。

由于模型建立的随机性,每次建立的模型都会存在差异。针对粗骨料体积分数分别为0、10%、20%、30%、40%、50%的混凝土,各建立10组数值模型。为了减少模型随机性引起的计算误差,每种粗骨料体积分数下取10组模型计算氯离子浓度的平均值进行分析。不同暴露时间下氯离子浓度沿深度的分布曲线如图7所示。从图7中可以看出,随着扩散时间的增加,相同深度处氯离子浓度也随之增加。为观察粗骨料体积分数对氯离子扩散的影响,分析在扩散时间t=1 080 d时不同粗骨料体积分数混凝土的氯离子浓度,如图8所示,随着粗骨料体积分数的增加,相同深度处氯离子浓度显著降低。如在距离混凝土表面12 mm 处,粗骨料体积分数为50%的混凝土中氯离子浓度相比于纯砂浆模型计算得到的氯离子浓度降低了51%。这说明与ITZ效应相比,粗骨料的稀释效应和曲折效应起主导作用。