容性耦合硅烷等离子体尘埃颗粒空间分布的二维流体模拟*

段蒙悦 贾文柱 张莹莹 张逸凡 宋远红†

1) (大连理工大学物理学院,三束材料改性教育部重点实验室,大连 116024)

2) (西南大学人工智能学院,重庆 400715)

基于自主研发的二维流体尘埃模型,研究了射频容性耦合硅烷等离子体放电中不同腔室结构对尘埃颗粒密度空间分布的影响.模拟发现,有别于一维模型,径向电场和作用在尘埃颗粒上的离子拖拽力径向分量是导致尘埃颗粒密度分布径向不均匀的主要因素,使其在极板边缘处呈现两个局部峰值,其中一个峰值表明尘埃颗粒有可能会克服电场力的支撑更接近极板.在极板半径较小或极板间距较小的情况下,径向离子拖拽力的作用增强,使尘埃颗粒更易于在极板边缘处和腔室侧壁附近聚集,出现环状尘埃颗粒分布带.在放电极板有介质材料包裹的情况下,尘埃颗粒密度径向分布的均匀性得到改善.最后,还模拟了单个尘埃颗粒在极板边缘处的涡旋运动规律.

1 引言

20 世纪80 年代末,IBM 研究团队的Selwyn等[1]在寻找芯片加工过程中的污染源时偶然发现,被加工基片上方悬浮了一层“尘埃云”.这些悬浮的尘埃颗粒实际上是由放电室中的反应性气体在放电过程中生成并聚集.特别地,在太阳能电池、各类晶圆的薄膜沉积过程中[2],射频容性耦合硅烷等离子体放电过程中更容易产生大量的尘埃颗粒.尘埃颗粒的出现,会造成腔室污染,进而影响加工器件的形貌、性能和可靠性.

自尘埃颗粒在实验室内被发现以来,研究者们针对尘埃颗粒在等离子体中的空间分布展开了广泛研究.结果发现,在一定条件下尘埃颗粒会在等离子体中形成许多复杂而有趣的物理现象,例如尘埃晶格、马赫锥、尘埃波、尘埃空洞和涡旋等[3-8].Goree 等[7]从实验和理论两方面分析了尘埃空洞产生的原因,他们认为尘埃粒子受到电场力和离子拖拽力共同作用导致了尘埃空洞的形成.随后,Chai 和Bellan[8]在实验中观察到了尘埃空洞和尘埃涡旋,并模拟提出尘埃颗粒的涡旋运动主要是由非保守力即离子拖拽力引起.事实上,在微重力条件下,更容易观测到尘埃颗粒在三维空间中形成的空洞和涡旋.Morfill 等[9]基于国际空间站建立的PKE 实验装置,观测到尘埃颗粒在腔室中心呈现出稳定的空洞,同时在极板边缘附近观察到两个稳定的尘埃涡旋流.通过建立二维氩等离子体的流体模型,Akdim 等[10]详细分析了微重力条件下尘埃颗粒所受到的各种力,最终得出结论是尘埃涡旋运动主要是粒子受到了离子拖拽力、电场力以及库仑排斥力的共同作用,与热泳力无关.

在地面实验条件下,射频容性耦合硅烷(SiH4)等离子体放电生成的尘埃颗粒尺寸一般在纳米量级.在忽略重力的影响下,Rozsa 等[11]利用激光散射仪测量了低气压SiH4气体放电中尘埃颗粒的空间分布,发现尘埃颗粒在两极板之间垂直于极板的轴向成双峰分布.随后,De Bleecker 等[12]采用一维流体模型模拟了SiH4放电中尘埃颗粒的输运、生长及分布情况,发现尘埃粒子受到的离子拖拽力和电场力共同影响了尘埃颗粒的轴向分布.基于一维流体耦合蒙特卡罗(MCC)模型,本课题组[13]详细分析了SiH4放电中放电气压、电压和频率等外部参数对尘埃颗粒分布的影响,发现尘埃颗粒的生成导致放电变得更具电负性,引起等离子体体区电场明显增强.

以上关于容性耦合SiH4等离子体尘埃颗粒分布的研究,均基于一维模型,而尘埃颗粒在平行于极板的径向力作用下,容易形成尘埃空洞、涡旋等其他现象.此外,放电腔室的结构对尘埃颗粒的径向分布也会造成影响.本文通过建立二维流体尘埃模型,研究了不同腔室结构下,包括介质环包裹的极板结构等,SiH4容性耦合等离子体放电中纳米尘埃颗粒密度的二维分布情况,着重分析了尘埃颗粒密度径向分布的变化.最后,还模拟了尘埃颗粒的涡旋运动规律.本研究能为SiH4等离子放电有关的薄膜沉积、微重力条件下尘埃颗粒的空间分布提供理论借鉴依据.

2 模型介绍

基于二维流体模型,等离子体中的所有粒子均由流体方程描述[14].具体地,电子由连续性方程、能量方程以及通量的漂移扩散近似共同决定[15],离子、中性粒子和尘埃颗粒由连续性方程和通量方程描述.

粒子所采用的连续性方程为

其中nj,Γj,Sj分别是粒子密度、通量和碰撞源项.

对于较高气压条件下,电子、离子和中性粒子动量平衡方程满足漂移扩散近似[15]:

其中µj和Dj分别为粒子的迁移率和扩散率,E为电场.

中性粒子、离子、尘埃颗粒进行冷流体近似,其中温度为常数.为获得电子温度,需要求解电子的能量方程:

其中能流通量及能量损失项分别为

尘埃颗粒漂移扩散方程表达式为[15]

离子渐近线倾角为π/2 时的碰撞参数为

在区间bc至线性德拜长度λDe之间的库仑对数积分为

正常情况下,尘埃颗粒在等离子体中受到电场力、重力、热泳力以及离子和中性粒子拖拽力的共同作用.而对于纳米级尘埃颗粒,所受的重力相对于其他力可以忽略[12].此外,在假定恒温的情况下,背景气体温度梯度产生的热泳力近似为零,因此本文尘埃颗粒主要受离子拖拽力和电场力的共同作用.

离子拖拽力由收集力和散射力两部分[16]组成,表达式如下:

电场力FE=QdE,Qd为尘埃颗粒表面所带电荷量,满足[17]:

其中Ie和Ii是流向尘埃表面的电子流和离子流,由模型自洽算出.电子流和离子流可以通过轨道运动限制理论[18]得到.

等离子体中的电场E和电势V通过泊松方程获得:

如果考虑上下极板外侧包裹的介质材料,泊松方程则为

其中εr是介质的相对介电常数,材料内部和表面上的电荷密度ρM可以根据电荷连续性方程得到[19].

需要说明的是,文中SiH4等离子体放电考虑了31 种粒子,包括11 种自由基、3 种正离子、8 种负离子和中性粒子,如表1 所列,具体化学反应可参考文献[13].原则上,利用气相化学反应的链式生长可以近似描述尘埃颗粒的成核、凝聚的起始过程,然而即使较小的尘埃颗粒也会包含上千个硅原子,模拟过程非常耗时,要想做到完全自洽也是不现实的.本文沿用前期工作的处理方法[13],为了简化计算,模拟硅烷的链式反应截止到和,并将这两种负离子作为产生尘埃颗粒的前驱粒子,将密度与链式反应系数的乘积作为尘埃颗粒的生成反应碰撞频率,代入连续性方程(1)的源项中,计算得到尘埃颗粒的密度.由于尘埃颗粒的充电时间在ms 量级[20],远远大于一个射频周期(几十纳秒)而小于尘埃颗粒的生长时间(s)[21],因此在模拟过程中,可以认为尘埃颗粒的悬浮电势及电荷量在一个射频周期内是恒定的.为提高计算效率,在模拟中尘埃颗粒的计算采用大时间步长,等离子体中的电子、离子和中性粒子采用小时间步长推进[12].

表1 除电子外,模型中包含的不同粒子情况Table 1.Overview of the different species incorporated in the model,besides the electrons.

为了研究尘埃颗粒在腔室中的涡旋现象,利用牛顿第二定律跟踪尘埃颗粒运动:

其中vd,FE,FI分别为尘埃颗粒的速度、所受到的电场力和离子拖拽力.

3 结果与讨论

放电腔室结构如图1 所示.上极板接射频电源φ=Vssin(2πft),下极板和侧壁接地;射频频率为13.56 MHz,电压幅值为50 V,放电气压为 1 Torr(1 Torr=133.32 Pa),中性气体温度为 400 K;腔室半径R1=10 cm,腔室间距z1=5 cm.

图1 放电腔室结构示意图Fig.1.Schematic diagram of the capacitive reactor.

首先讨论等离子体中电子、尘埃颗粒以及SiH4放电中最主要的正、负离子的密度二维分布情况,其中极板间距z0=3 cm,电极半径R0=9 cm,如图2 所示.可以看出,体区正负离子密度远高于电子密度,符合电负性气体放电的主要特性,如图2(a)—(c)所示.与其他粒子不同,尘埃颗粒主要分布在上下两个极板附近,以及极板与腔室侧壁之间,如图2(d)所示.尘埃颗粒密度沿轴向(z方向)呈马鞍形分布,这与一维尘埃模型[13]结果相同,是轴向电场力和轴向离子拖拽力的共同作用的结果,使尘埃颗粒在上下鞘层边界处达到平衡,由图3(a),(c)可知.然而,二维模拟结果中可以发现,尘埃颗粒密度沿径向(r方向)分布极不均匀,在靠近极板边缘处的r1=8.9 cm (点1)和r2=9.5 cm (点 2)出现两个极大值,且点2 处的峰值更高.事实上,尘埃密度的径向分布当然也与电场力以及离子拖拽力密切相关.在靠近极板边缘处,除了电场力和离子拖拽力的轴向分量,其径向分量也逐渐变得重要,特别是离子拖拽力的径向分量变化显著,这成为影响尘埃颗粒分布的重要因素,如图3(b)和图3(d)所示.

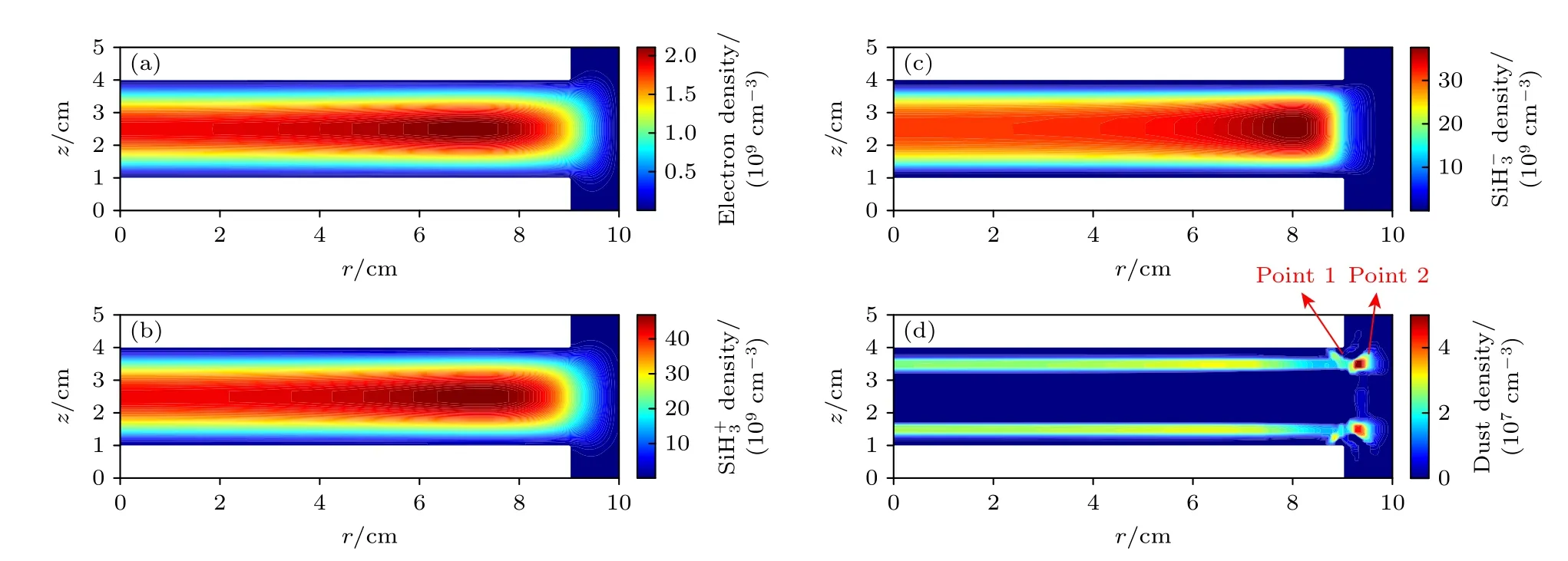
图2 z0=3 cm,R0=9 cm 时,等离子体中的密度空间分布 (a)电子;(b) 正离子;(c) 负离子;(d)尘埃颗粒Fig.2.Spatial density distributions in plasma at z0=3 cm and R0=9 cm: (a) Electron;(b) ;(c) ;(d) dust particles.

图3 z0=3 cm,R0=9 cm 时,尘埃颗粒所受电场力(a)轴向分量、(b)径向分量,以及离子拖拽力(c)轴向分量、(d)径向分量的二维空间分布Fig.3.Spatial distributions of (a) axial component and (b) radial component of the electric field force,(c) axial component and (d)radial component of the ion drag force at z0=3 cm and R0=9 cm.

为进一步分析尘埃颗粒密度径向分布的影响因素,图4(a)给出径向离子拖拽力(FIr)在靠近上极板鞘层处(z=3.88 cm)沿着r方向的变化情况,其中z=3.88 cm 为经过尘埃密度的两个峰值位置.由图4(a)可知,图中点1 位置左端,离子拖拽力的径向分量FIr＞0 ,说明其方向指向腔室侧壁,可拉动尘埃颗粒向侧壁方向移动;而图中点1 右端,离子拖拽力的径向分量FIr＜0 ,其方向指向腔室内部,拉动尘埃颗粒远离侧壁;而点1 位置处于FIr为零的附近,加上该点微弱的电场力径向分量(图3(b)),尘埃颗粒在此处达到平衡,可稳定地存在,分布形成峰值.同样地,点2 位置左端的尘埃颗粒受到较大的离子拖拽力径向分量,拉动尘埃颗粒不断向侧壁移动,直到在点2 位置处与侧壁处的电场力达到平衡,形成较大的密度分布峰值.

图4 (a) z=3.88 cm 时,径向离子拖拽力随r 的变化;(b) 正离子通量矢量图(极板间距z0=3 cm,电极半径R0=9 cm)Fig.4.(a) Radial component of the ion drag force along r direction at z=3.88 cm;(b) flux vector map of (Gap distance z0=3 cm and the electrode radius R0=9 cm).

另外,可以注意到图2(d)中点1 位置的尘埃密度峰值更加靠近上极板,说明此处径向离子拖拽力的作用使得尘埃颗粒有脱离电场力的支撑而更加接近极板的趋势.图4(b)给出了上极板边缘附近(z=2.5—5.0 cm,r=8.0—10.0 cm)通量矢量图.由图可知,正离子通量矢量线在靠近上极板边缘内侧附近聚焦于A区域且逐渐紧密,说明尘埃颗粒受到很大的离子拖拽力迫使其向A区域聚集.其实在工业应用中,尘埃颗粒也就是黄粉,一般会在断电瞬间由于缺少电场力的作用会掉落到基片对薄膜造成损伤.但是,从本文二维模拟中可以预测,即使没有切断电源,在某些特殊参数条件下,径向电场的增强和径向离子通量的增大,也会在极板边缘处出现黄粉的聚集,这是薄膜沉积工艺不愿意看到的.

图5 极板间距z0=3 cm,极板半径不同时, 密度(a)—(c),尘埃颗粒密度(d)—(f),离子拖拽力径向分量(g)—(i)的二维空间分布情况 (a),(d),(g) R0=9 cm;(b),(e),(h) R0=8 cm;(c),(f),(i) R0=7 cmFig.5.Spatial distributions of densities (a)—(c),dust particles densities (d)—(f) and radial component of the ion drag force(g)—(i) at the different electrode radius and z0=3 cm: (a),(d),(g) R0=9 cm;(b),(e),(h) R0=8 cm;(c),(f),(i) R0=7 cm.

图6 电极半径R0=8 cm,极板间距不同时, 密度(a)—(c),尘埃颗粒密度(d)—(f),离子拖拽力径向分量(g)—(i)的二维空间分布情况 (a),(d),(g) z0=3.0 cm;(b),(e),(h) z0=2.0 cm;(c),(f),(i) z0=1.4 cmFig.6.Spatial distributions of (a)—(c) densities,(d)—(f) dust particles densities and (g)—(i) radial component of the ion drag force at the different electrode spacing and R0=8 cm: (a),(d),(g) z0=3.0 cm;(b),(e),(h) z0=2.0 cm;(c),(f),(i) z0=1.4 cm.

图7 为上下两极板边缘处有、无介质层包裹的情况下,正离子密度以及尘埃颗粒密度的二维空间分布情况.“极板边缘”是指在极板8—9 cm处,使用长度为1 cm 的介质材料进行包裹,其中介质材料使用泊松方程(9)式.可以看到,在有介质层的情况下,正离子密度更加均匀地分布在两极板之间,且密度值较无介质层的情况高,如图7(a),(b)所示,相当于等离子体被拉回到两个极板之间,进而导致尘埃颗粒在r＜ 6.5 cm 的径向范围内具有较好的均匀性,且密度较无介质层的情况高,如图7(d)所示.这主要是由于介质层会抑制边缘效应,等离子体的均匀性得到优化.由图7(d)还可以发现,在上下极板介质层的两侧,分别出现了两处更加靠近极板的尘埃颗粒密度流,这同样是由于正离子通量聚集在介质层两侧,进而使该处的离子拖拽力相对增强造成的,同图4(b)所述.由以上模拟结果可以看出,在工业生产中,介质材料的应用能明显改善两极板之间放电的均匀性,但在介质边缘处黄粉(尘埃颗粒)也会更多地聚集和偏向极板,进而影响沉积工艺.根据本文研究内容,可适当减小极板半径或极板间距,使尘埃颗粒尽量远离极板,避免放电熄灭后掉落在基片上对薄膜造成的损伤.

图7 z0=3 cm,R0=9 cm 时,上下极板在无介质层包裹和有介质层包裹的情况下 密度(a),(b)和尘埃颗粒密度(c),(d)Fig.7.Spatial distributions of densities (a),(b) and dust particles densities (c),(d) in the case of discharge electrode without or with dielectric materials at z0=3 cm and R0=9 cm.

此外,还模拟了极板间距z0=3 cm,极板半径R0=9 cm 的情况下,单个尘埃颗粒的涡旋运动轨迹.从图8(a),(b)可以看到,尘埃颗粒随着时间的变化呈涡旋运动,在靠近上极板边缘位置呈顺时针运动,靠近下极板呈逆时针运动,该结果与PKE[9]实验中观察到的涡旋现象一致.为了更好地显示尘埃颗粒的涡旋运动轨迹,图8(c)—(f)为尘埃颗粒的轴向、径向位置随时间的演化过程.可以看出,无论上极板还是下极板边缘附近的尘埃颗粒,其轴向和径向位置随时间演化均展现出正弦波的特点,但是二者轴向位置在每个时刻上方向相反,相位差为 π (图8(c),(d)),而径向位置二者没有差别(图8(e),(f)),这是导致上、下极板边缘处尘埃颗粒呈相反方向涡旋运动的主要原因.事实上,尘埃颗粒所受到的电场力为保守力,旋度为0,若所受到的离子拖拽力旋度也为零,尘埃颗粒必然不会形成涡旋运动,这也从侧面证明了尘埃颗粒所受到的离子拖拽力为非保守力.

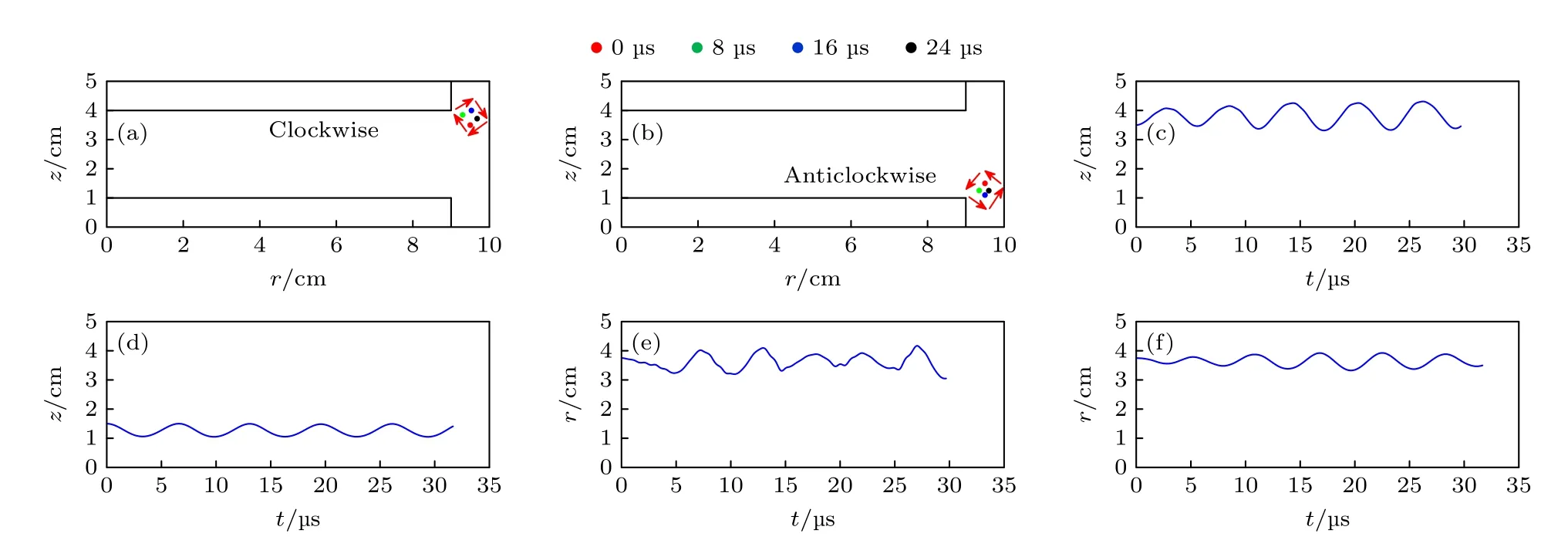
图8 上极板边缘(a)和下极板边缘(b)位置处的尘埃颗粒涡旋运动轨迹;尘埃颗粒轴向位置(c),(d)及径向位置(e),(f)随时间演化过程(极板间距z0=3 cm,电极半径R0=9 cm)Fig.8.Vortex trajectory of dust particles at the edge of (a) the upper plate and (b) the lower plate;axial position (c),(d) and radial position (e),(f) of dust particles over time (Gap distance z0=3 cm and the electrode radius R0=9 cm).

4 结论

通过建立二维流体模型研究了不同腔室结构下,射频容性耦合硅烷等离子体放电中尘埃颗粒的二维空间分布情况.研究发现,除了轴向电场力和离子拖拽力的共同作用使尘埃颗粒聚集在上下极板的鞘层边界处,在极板边缘附近,径向电场力和径向离子拖拽力的明显增大会使尘埃颗粒密度沿腔室径向分布变得不均匀,在靠近极板边缘处出现两个局部的密度峰值,其中一个峰值所在位置是尘埃颗粒趋于克服电场力的作用而接近极板所致.对于极板半径较小、极板与侧壁间距增大的情况,不同方向的离子拖拽力径向分量驱使尘埃颗粒分别向腔室侧壁或极板边缘聚集,导致类似环状的尘埃颗粒分布带的出现.另外,随着放电腔室内上下极板之间的放电间距减小,等离子体主要分布于极板边缘与腔室侧壁之间,尘埃颗粒也相应地聚集在极板与侧壁之间,进而在腔室中心形成明显的尘埃空洞,极板和侧壁之间形成的“环状分布带”也更加明显.在介质材料包裹上下极板的情况下,研究发现,无论是放电产生的正离子密度还是尘埃颗粒密度,在两极板之间均形成较好的径向均匀性,且密度值均较无介质材料的情况高.最后,通过跟踪单个尘埃颗粒随时间的运动情况,发现尘埃颗粒在腔室中的上、下极板边缘位置呈旋转方向相反的涡旋运动,这主要是由非保守的离子拖拽力作用造成的.

本文研究结果可以为与硅烷等离子体放电有关的薄膜沉积工艺或微重力条件下,尘埃颗粒的空间分布和输运特性研究等提供理论借鉴依据.可通过适当调整极板半径或极板间距,或在极板边缘处包裹介质层等办法,改变尘埃颗粒密度空间分布,例如在沉积薄膜工艺中可以避免在极板边缘处形成尘埃颗粒聚集,有效避免黄粉(尘埃颗粒)掉落在基片上对薄膜造成的损伤.