NO+离子系统热力学性质的理论研究*

胡敏丽 房凡 樊群超† 范志祥‡ 李会东 付佳 谢锋

1) (西华大学理学院,高性能科学计算四川省高校重点实验室,成都 610039)

2) (清华大学核能与新能源技术研究所,先进核能技术协同创新中心,先进反应堆工程与安全教育部重点实验室,北京 100084)

基于课题组前期获得的研究双原子分子某电子态完全势能函数改进后的Hulburt-Hirschfelder (improved Hulburt-Hirschfelder,IHH)势能模型,结合实验测量得到的光谱常数和Rydberg-Klein-Rees (RKR)光谱数据,对NO+离子基态包含离解区在内的全程势能曲线进行研究.利用获得的完全势能曲线数值求解一维薛定谔方程,得到了体系包含高激发态在内的振转能级,并以此为基础计算获得体系总的内部配分函数,最后借助量子统计系综理论计算NO+离子系统在100—6000 K 温度内的摩尔热容、摩尔熵、摩尔焓和约化摩尔吉布斯自由能.对NO+离子系统的研究结果表明,IHH 势模型同样也适用于离子系统,计算的势能曲线与实验数据吻合良好,其精度优于HH 势和MRCI/aug-cc-pV6Z 势,且预测的热力学性质较HH 势模型更接近实验值.本文提出的研究方法为通过双原子离子微观信息获取系统宏观热力学性质提供了一条新的有效途径.

1 引言

离子系统的宏观热力学性质对农业、化学、工程、物理和生物科学等领域的发展具有重要意义[1−5],它不仅是测量热效应和区分反应过程的重要依据,而且是确定化学反应方向的重要判据.近年来,许多研究团队对双原子离子的热力学性质进行了相关研究.

早在1970 年,Horton[6]利用近似配分函数、比自由能和比焓的解析表达式,给出了OH+,CH+,等离子在T≥3000 K 时的比自由能和比焓.1989 年,Bartl 和Bartlova[7]采 用MGM (Mayer,Geppert-Mayer)方法和直接求和法计算了,SiF+等离子的配分函数和振转能级,得到了体系在1000—15000 K 温度内的热容和熵等标准热力学函数.2001 年,Peterson 等[8]采用单双耦合聚类方法,确定了BBr+和BBr–离子的势能函数,进而计算了其光谱常数和热力学性质.2005 年,Capitelli等[9]获得了与火星大气相关的CN+和CO+等离子在50—50000 K 温度内的热力学性质,为高温混合气体热力学模型的研究提供了重要的数据支撑.2016 年,Maltsev 等[10]通过Morse 势和远距离静电吸引势构造了VAr+和CoAr+的内部配分函数,得到了这两个离子在298.15—104K 温度内的热容、熵和焓等热力学量.2018 年,Qin 等[11]使用Rydberg-Klein-Rees(RKR)方法获得了和CO+

等离子较低电子态的势能曲线,并求解薛定谔方程确定了振动能级,计算了和CO+等离子在平衡和非平衡状态下的热力学性质.2021 年,Liang 等[12]利用双温模型推导了热容方程,并计算了等离子在5×104K 温度下的热容,与ESA 表的误差在15%以内.2022 年,Euybe 等[13]通过修正后的双曲势能(modified hyperbolical-type potential,MHTP)模型,利用Varshni 条件得到了束缚态振动能级和热力学函数表达式,研究了SiF+和离子的热容、熵等热力学函数.近年来,Maltsev 等[14−17]考虑自旋轨道和自旋分裂,通过从头计算方法确定了ArN+,,ArH+,ArO+等离子基态和激发态的原子间相互作用势,进而得到了这些离子在298.15—104K 温度范围内的配分函数和热容、焓等热力学性质.

上述理论方法为双原子离子系统宏观热力学性质的研究作出了重要贡献.虽然研究者们可以通过精确的势能函数来确定离子的配分函数从而计算系统的宏观热力学量,但许多势能函数对于复杂的双原子体系构建的势能曲线在长程区域附近难以取得令人满意的结果,因此最终计算获得的系统热力学性质其误差精度也受到了一定的影响.

最近,Tian 等[18]重新构建获得了研究双原子分子某电子态完全势能函数改进后的Hulburt-Hirschfelder (improved Hulburt-Hirschfelder,IHH)势能模型,并将该模型应用于计算部分双原子分子体系的内部配分函数,所得结果与实验数据符合得很好.除双原子分子体系外,在双核离子体系中,NO+离子作为大气层的重要组成部分,也是星际云中最稳定的双原子阳离子之一[19],其离子结构与性质在生物、原子分子物理等领域一直受到广泛关注[20−25].本文从IHH 势能模型出发,首先构建NO+离子的全程势能曲线,然后求解一维薛定谔方程确定其包含高激发态在内的振转能级,从而建立体系总的内部配分函数,最后通过量子统计系综理论计算系统的摩尔热容、摩尔熵、摩尔焓和约化摩尔吉布斯自由能,并将计算结果与美国国家标准与技术研究院数据库(NIST)实验数据[26]进行比较和分析.

2 理论与方法

对于简单的双核离子系统,首先利用离子体系精确的势能曲线有效构造体系的配分函数,再借助量子统计系综理论获得离子的宏观热力学量.IHH 势能函数表示为[18]

式中r为核间距,De为离解能,ωe为振动光谱常数,Be为转动光谱常数,re为平衡位置,σ1,σ2为无量纲常数.

式中ωe,ωeχe为振动光谱常数,αe,Be为转动光谱常数.变分基函数q定义为

式中,λ为可调变分参数.IHH 势能函数的迭代过程是对双原子分子电子态RKR 数据的拟合.λ的最优值由最小方均根误差(root-mean-square deviation,RMSD)确定.

其中,VIHH为IHH 势,VRKR为RKR 势,NP为RKR数据点数目.

通过IHH 势能函数,构建体系的势能曲线,代入薛定谔方程[29]可得体系的完全振转能级Eυ,J:

式中,µ为体系的约化质量,ℏ=h/(2π),h为普朗克常数,υ,J分别为振动量子数和转动量子数,VJ(r)为体系的势能函数,φυ,J(r) 为体系的波函数.而体系的振转能级Eυ,J可借助LEVEL 程序[29]数值求解.

在不考虑自旋相互作用时双原子离子的内部配分函数可表示为[30]

式中σ为对称因子(同核分子σ=1/2,异核则为σ=1),n为电子量子数,(2-δΛ,0)(2S+1) 为电子简并度,Λ和S分别为电子轨道角动量投影到核间轴上的量子数和电子自旋角动量量子数;(2J+1)为转动简并度,c为光速,ε0为最低能级,kB为玻尔兹曼常数,T为开氏温度.另外,离子平动配分函数表示为[31]

其中V为体积.则体系总的配分函数为[32−34]

利用构造的配分函数,通过量子统计系综理论即可求得体系的摩尔热容Cm为

其中NA为阿伏伽德罗常数.体系的摩尔熵Sm为

体系的摩尔焓Hm为

体系的摩尔吉布斯自由能Gm为

相对摩尔焓、约化摩尔吉布斯自由能分别为

式中,H298.15为T=298.15 K 时的摩尔焓值.另外,采用RMSD 验证IHH 势模型预测热力学性质的准确性:

其中,N为该离子某一热力学性质数据点的个数,Pcal和Pexpt为该离子热力学性质的计算值与实验值.

3 应用与讨论

热力学性质在宏观层面揭示了系统的能量变化,掌握气体全面的热力学数据是探索星际气体组成的关键[9].本文采用HH 势及IHH 两种势模型,分别研究了NO+离子宏观气体的摩尔热容、摩尔熵、相对摩尔焓、约化摩尔吉布斯自由能.

首先应用HH,IHH 势模型,分别计算NO+离子全程势能曲线,并与MRCI/aug-cc-pV6Z (简称MRCI)计算的势能曲线结果[35]进行对比分析.本文所需NO+离子基态的6 个分子常数[36],包括ωe,ωeχe,Be,αe,re和De.唯一可调节的参数λ由IHH 势与RKR 势[36]的最小方均根误差确定,最优值为1.045.表1 为使用IHH 势、HH 势、MRCI计算的势能值[35]与RKR 实验值[36]的绝对误差值和方均根误差值,其中,IHH 势与RKR 势的方均根误差为96.9 cm–1,而HH 势的方均根误差为112.7 cm–1,MRCI 势能曲线[35]的方均根误差为133 cm–1,这表明IHH 势在平衡位置附近具有更高精度.而在原子间距较大的渐近区和离解区,本文将结合体系的微观振转能级,求解其宏观热力学量进一步验证IHH 势模型的可靠性.

表1 NO+离子不同势能及其与RKR 实验值[36]的误差值Table 1.Different potential energy of NO+ ion and its absolute error with the experimental value of RKR[36].

其次,对IHH 势,HH 势,MRCI 势[35]以及实验RKR 势[36]进行可视化对比分析,如图1 所示.IHH 曲线与HH 曲线、MRCI 曲线[35]在短程区间(1 .19 Å ≤r≤1.69 Å)与实验RKR 数据[36]吻合良好;在长程区域(1 .69 Å ≤r≤5.01 Å),随着核间距增大,IHH 势迅速收敛于离解能,而HH 势和MRCI 势[35]收敛较缓慢.在长程区域内IHH 势,HH 势与MRCI 势[35]三者之间出现明显的偏差.基于此客观事实,将借助IHH 和HH 两种势函数计算得到的热力学量来进一步验证IHH 和HH 两种势函数的可靠程度.

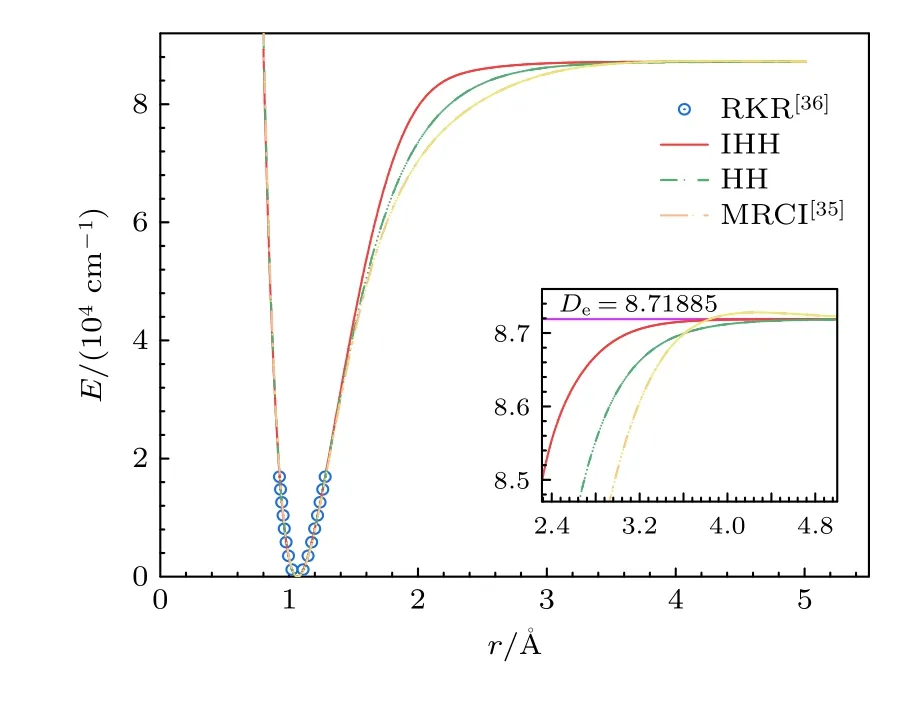
图1 NO+离子的势能曲线对比Fig.1.Comparison of potential energy curves of NO+.

在获得NO+离子的全程势能曲线后,利用LEVEL 程序可确定其完整的振转能级,通过构造体系总的配分函数,并结合量子统计系综理论,进一步得出NO+离子在100—6000 K 温度内的宏观热力学量.表1 给出了基于HH,IHH 势模型计算的热力学数据与NIST 实验数据的方均根误差,图2—图6 给出了使用两种势模型计算的内部配分函数、热力学量与实验值的比较图.图2 给出了基于IHH 势得到的内部配分函数值(灰色实线)、通过HH 势获得的内部配分函数值(绿色虚线)以及Barklem 和Collet[37]的数据结果(粉色圆点).可以看出,尽管IHH 和HH 的结果在整个温度范围内与Barklem 和Collet[37]的结果吻合很好,但从相对误差曲线中可知,在较高温度范围区间,HH 结果与Barklem 和Collet[37]的值偏差更大.

图2 NO+离子的内部配分函数与其他数据[37]结果对比(ARE 为相对误差的绝对值)Fig.2.Comparison of internal partition function of NO+and other data[37] (ARE means the absolute relative errors).

摩尔热容Cm是实验中常用的物理量,在表2中基于IHH 势模型计算的Cm的方均根误差为0.021733 J/mol K,小于HH 势的方均根误差.另外,图3(a)展示了通过IHH 势得到的摩尔热容值(灰色实线)、基于HH 势获得的摩尔热容值(绿色虚线)以及NIST 实验热容值(粉色圆点)[26].随着温度T的升高,Cm逐渐增大,在800—1200 K 温度内增长较快,随后增长较缓趋于平稳;在5000—6000 K 区域,,相比而言更接近实验值.图3(b)展示了两种势模型摩尔热容值相对误差随温度的变化规律,随着温度升高,二者的相对误差出现增大趋势,在同一温度下(T≥1800 K),HH 势能模型摩尔热容值相对误差均大于IHH 的结果.这说明在高温下,精确的振转能级信息更能有效影响热力学量的计算精度,相比而言,基于IHH 势模型得到的结果更优.另外,通过分析相对摩尔焓 ΔH,摩尔熵Sm和约化摩尔吉布斯自由能Gr的计算结果也发现了类似结论.从表2 可以看出基于IHH 势模型计算的NO+离子 ΔHIHH的方均根误差为0.034329 kJ/mol,为0.02293 J/(mol·K),为0.017711 J/(mol·K),均小于HH 势的误差.

图3 NO+离子摩尔热容与NIST 实验数据[26]对比Fig.3.Comparison of molar heat capacity of NO+ and NIST experimental data[26].

表2 HH,IHH 势模型计算得到的NO+离子不同热力学性质的RMSDTable 2.RMSD of HH and IHH potential models for different thermodynamic properties of NO+ ions.

图4—图6 分别展示了NO+离子的 ΔH,Sm和Gr随温度的变化,也给出了两种势模型的预测值与实验值的相对误差曲线.在温度较低时,两种模型的相对误差曲线相互重叠;随着温度升高,两者的误差均逐渐增大,其曲线走向出现较大偏离.当温度达到T=6000 K 时,基于HH 势模型的ΔH偏差升高到0.110%,Sm偏差提升到0.023%,Gr偏差升高到0.012%,而此时,IHH 势计算的 ΔH最大偏差为0.044%,Sm为0.012%,Gr为0.008%,其计算结果精度均优于HH 势.这些结果再次验证了用于计算热力学量振转能级的精确性,进一步说明IHH 势模型的可靠性.

图4 NO+离子相对摩尔焓与NIST 实验数据[26]对比Fig.4.Comparison of the molar enthalpy increment of NO+and NIST experimental data[26].

图5 NO+离子摩尔熵与NIST 实验数据[26]对比Fig.5.Comparison of the molar entropy of NO+ and NIST experimental data[26].

图6 NO+离子约化摩尔吉布斯自由能与NIST 实验数据[26]对比Fig.6.Comparison of the reduced molar Gibbs free energy of NO+ and NIST experimental data[26].

综上所述,IHH 势模型可以较好地预测双原子离子气体的宏观热力学性质.两种理论模型的方均根误差和相对误差曲线表明,IHH 模型在预测气态NO+离子的摩尔热力学量方面优于HH 模型.而这种无需使用大量实验参数的方法可为计算其他气体的热力学性质提供有效途径.

4 结论

首先采用IHH 势模型构建基态NO+离子的解析势能曲线,分析表明,在平衡位置附近,IHH 曲线,HH 曲线与MRCI 曲线差异较小并与RKR 数据吻合,但IHH 势与实验数据的方均根误差小于HH 势和MRCI 势的结果,而在长程区域IHH 势要高于HH 势和MRCI 势,借助LEVEL 程序计算得到了NO+离子精确的完全振转能级,以此获得其内部配分函数.最后预测了NO+离子在100—6000 K温度内的摩尔热容、摩尔熵、摩尔焓和约化摩尔吉布斯自由能.结果表明,通过IHH 势模型计算的热力学性质获得的结果比采用HH 势模型更接近实验值,整体误差更小.因此,本文结论是气态双原子离子精确的微观结构信息,对于体系的热力学性质至关重要,构建可靠的解析势能函数获得体系精确的能级信息,并结合量子统计系综理论,是一种快速获得气态双原子离子热力学量的可行方法,同时可为其他双原子体系的分析与研究提供重要参考.