多孔介质内气泡Ostwald 熟化特性三维孔网数值模拟*

2023-09-06张沐安王进卿吴睿冯致詹明秀徐旭池作和

物理学报 2023年16期

张沐安王进卿† 吴睿冯致詹明秀徐旭池作和

1) (中国计量大学计量测试工程学院,杭州 310018)

2) (上海交通大学机械与动力工程学院,上海 200240)

多孔介质内气泡的Ostwald 熟化行为广泛存在于CO2 地质封存、多孔材料制备、燃料电池等领域.为探究孔隙尺度下多孔介质内气泡的熟化特性,建立了基于浓度耦合计算的三维孔隙网络模型,该模型考虑了气泡形态、多孔介质结构以及气液之间的传质,通过求解三维孔隙网络内各孔体的气相浓度,得到各气泡的演化过程,并采用四孔隙结构微流体芯片可视化实验验证了模型的可靠性.为分析多孔介质非均质性对气泡熟化过程影响,构建了两种不同孔隙尺寸的三维孔网结构,对两个区域内的气泡熟化过程进行了数值模拟.结果表明: 气泡初始分布会对熟化过程产生影响,当气泡非均匀分布时,气泡从小孔隙区域传输至大孔隙区域的同时,也会各自向自身区域的大气泡区域传质;气泡初始尺寸的差异,会加速熟化进程,使熟化时间明显短于均匀分布状态.孔隙数的选取对平均毛细力、饱和度等连续尺度等效参数具有显著影响,孔隙数增加时毛细力与饱和度呈现更具规律性的非线性变化.该模型的建立可以预测地质封存过程中CO2 的演化过程,为CO2长期封存过程中非均质性的影响机制研究提供指导.

1 引言

气泡Ostwald 熟化效应是一种在气液两相流体系中,受气泡间不同毛细压力的影响,小气泡通过润湿相分子扩散将自身质量传递给附近大气泡的现象.毛细力决定气泡间浓度分布,浓度梯度驱动的扩散效应是传质的主导机制.该过程普遍存在于自然界及能源、化工、生化和环境保护等领域,如超疏水表面自清洁技术[1,2]、油水分离工艺[3]、岩浆脱气[4,5]、多孔材料制备[6,7]和CO2地质封存[8,9]等.最典型的是在CO2地质封存中,这种熟化效应会引起CO2气体在局部区域的重新聚集,增加了地质储存泄漏的风险[10,11].因此,对多孔介质内气泡熟化特性的研究至关重要.

Ostwald 熟化效应可根据空间状态分为自由流体空间与受限空间(多孔介质)熟化两种形式.早在20 世纪众多国内外学者已经对气泡在溶液中的熟化特性进行研究,提出并改进了气泡簇半径与时间的稳态生长理论[12-15].在自由流体中,气泡熟化可以不受空间限制,呈现标准的Ostwald 熟化现象.而在多孔介质中,空间结构限制会增加Ostwald熟化过程的复杂性.目前,国内外学者已对多孔介质环境下的熟化效应进行了广泛的实验研究.Xu 等[16]在实验过程中成功捕捉到小气泡与大气泡的熟化过程,验证了CO2地质封存过程中Ostwald 熟化机制的存在;Xu 等[17]通过2.5D 玻璃微流体芯片实验发现气泡在均质多孔介质内的熟化受限于孔喉的几何结构,最终气泡尺寸趋于一致,发生反Ostwald 熟化效应.Ostwald 熟化是长时间尺度的过程,在毫米尺度空间域,CO2达到毛细平衡需要数月至数年的时间,而对于米级系统,熟化则需要一万年甚至更久[18].可见实验仅能对短时间内的熟化效应进行研究,采用数值模拟方法对长时间尺度气泡熟化过程进行预测是有效手段.

在Ostwald 熟化数值模型的建立方面,相关的研究工作主要集中在孔网模型方面.孔网模型的核心思想是将孔隙结构简化为孔隙和孔喉的组成[19-21],从而对其中内部平衡问题和传质计算进行简化.与直接模拟法(DNS)相比具有计算范围广、计算效率高的优点,能够较好地反映多孔介质内孔隙结构对扩散过程的影响,揭示传质过程孔隙尺度机理.Xu 等[22]通过双气泡孔网模型证明重力会诱导CO2向上迁移影响多孔介质内Ostwald 熟化,并放大孔隙尺度得到一维连续介质模型以评估CO2地质封存安全性;Xu 等[23]基于实验建立了能准确预测气泡演变的均质孔网模型,并指出多孔介质内孔喉的结构会影响Ostwald 熟化方向;Mehmani 等[24]通过孔网模型模拟混相气泡的熟化过程,提出一种完全隐式算法求解多孔介质内被捕获气泡的演化过程,并开发了一种预测气泡稳定平衡分布状态理论,证明气泡在非均质多孔介质中的平衡比均匀介质中的平衡要慢得多.以上文献主要在一维和二维条件下开展数值研究,而自然界和工业上的问题多为三维多孔介质.Chalendar 等[25]建立了一种三维锥形孔喉数值模型,模拟地质封存时CO2气泡演化,通过算法寻找每个有效扩散路径并对每条路径的传质进行叠加,实现了对简单连续气泡群演化时间尺度的数值模拟.但该模型随着熟化过程中气泡数量减少,可搜索的有效扩散路径数量大幅增加,算法复杂度将呈指数增长.

基于质量守恒与气液传质方程,本文构建一种通过耦合计算每个孔隙中气相浓度场来获得气泡生长速率的孔隙网络数值模型.该模型考虑气泡形态、多孔介质结构以及气液之间的传质,并通过四孔隙结构微流体芯片可视化实验验证模型的可靠性.最后以CO2地质封存为研究背景,采用该模型对包含两种不同孔隙尺度多孔介质内的气泡熟化过程进行三维数值模拟,分析气泡初始分布和孔隙数对熟化的影响特性,并探究孔隙尺度平均毛细力与饱和度的关系,为后续的连续尺度熟化机制研究提供指导.

2 数值计算模型

2.1 基本方程

气泡熟化过程主要受3 个方程控制: 拉普拉斯方程、亨利定律和菲克定律:

式中,pn为气泡内部毛细压力,ps为溶液压力,Ra和Rb分别为气泡的平面和层面曲率半径,C为溶质的浓度,A为两气泡间扩散面积,L为两气泡间扩散距离.本文计算时选用的扩散面积与扩散距离如图1 所示,其中A1为气泡1 与喉道切线对应的弧面面积,A2为喉道截面积,A3为气泡2 与喉道切线对应的弧面面积;L1为气泡1 到孔体的距离,L2为喉道长度,L3为气泡2 到孔体的距离.因此,扩散面积A与扩散距离L之比为

图1 双气泡系统传质过程Fig.1.Two-bubble system mass transfer process.

2.2 计算模型

2.2.1 模型框架

建立的孔网模型假设熟化过程是准静态的,只考虑气体扩散作用.在整个孔隙网络中,孔体为圆柱体结构,喉道为长方体结构,当气泡直径小于孔体深度时,气泡为球形气泡,其余情况气泡为圆柱形气泡.同时做出以下假设: 气泡与液相均处于局部热力学平衡状态,即溶解与生长都是瞬时的;一个孔体内只能存在一个气泡且不可移动,在整个溶解或生长过程中,气泡质量中心始终与孔体中心重合;当气泡尺寸达到孔体尺寸后,气泡即停止生长,不侵入喉道.

如前所述,国内外学者已对Ostwald 熟化问题开展了数值研究,不同于他们建立的数值模型,本模型通过计算孔体内的气相浓度分布得到气泡生长速率,使整个计算过程更加简便,提高了计算效率.如图2 所示,该模型会依次判断各孔体内是否存在气泡以及该孔体周围充满液相的孔体个数,并根据孔体内是否存在气泡将(3)式中的浓度计算分为两种情况: 当孔体内为气泡时,根据拉普拉斯方程和亨利定律求解气泡浓度;当孔体内为液相时,基于质量守恒方程建立线性方程组求解孔体内气相浓度.以下对两种情况的浓度计算进行介绍.

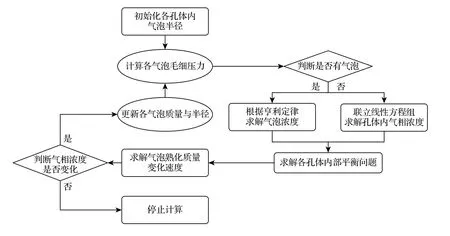
图2 计算程序算法流程图Fig.2.Flow chart for the calculation algorithm.

2.2.2 孔体内为气泡

如图3(a)所示,孔体i内存在气泡i,其相邻六个方向的孔体j内均存在气泡j.根据这些气泡的初始半径,代入(1)式和(2)式可以分别得到i和j孔体中气相浓度Ci与Cj,即

图3 数值计算模型 (a)孔体i 内为气泡;(b)孔体i 内为液相Fig.3.Numerical calculation model: (a) Pore body i with a bubble;(b) pore body i filled with liquid phase.

2.2.3 孔体内为液相

当孔体i内充满液相时,无法依据拉普拉斯方程与亨利定律求解气相浓度Ci,需基于质量守恒与气液传质方程建立线性方程组求解.构建的孔网模型考虑了孔体连接方式的结构化,即每个孔体周围都有6 个孔隙连接.如图3(b)所示,孔体i中充满液相,相邻6 个方向的孔体j内均存在气泡j,根据气泡j的初始半径,代入(5)式可分别得到相邻气泡的气相浓度Cj,则充满液相的孔体i中气相浓度Ci可基于传质方程(6)求解:

在整个三维孔网模型中,孔体内气泡与液相随机分布,因此对于孔体i内充满液相的情况,需要依次判断周围孔体j是否充满液相,建立关于浓度的线性方程组,并采用BiCGSTAB 方法[26]求解出充满液相的孔体内气相浓度.根据各孔体的气相浓度,可以得到气泡的生长速率.气泡i通过熟化效应在单位时间变化的质量为该气泡与其相邻气泡传递质量的和,见(7)式.当熟化系统中所有孔隙内的气相浓度相等时,熟化结束,停止计算.

2.2.4 时间步长

在该程序中,一个时间步长为整个孔隙空间内所有气泡中半径增大或减小指定长度R'所需要的最短时间.因此,时间步长会随着熟化程序的迭代进行自动优化.在熟化初期,气泡间尺寸半径差异大,熟化速率快,时间步长短;而熟化后期,熟化速率减慢,时间步长增大.本文计算模型选取的R'值为0.1 µm.

(8)式为适用于球形与圆柱形气泡的体积公式,计算程序中单次输出的熟化时间步长为

2.3 计算对象

在实际多孔介质环境中,多孔介质结构通常呈现非均质性,为了探究孔隙结构非均质性对熟化过程的影响,选取了由两种不同孔隙尺度区域构成的三维孔网结构作为计算对象,对两个区域内的气泡熟化过程进行数值模拟.如图4 所示,小孔隙区域、大孔隙区域孔体半径分别为20 和50 µm,两个区域深度均为30 µm;所有喉道半径均为5 µm,深度为5 µm.

图4 多孔隙结构熟化模型Fig.4.Multi bubble ripening model.

在孔隙尺度,气泡群初始分布会显著影响熟化过程,气泡群非均匀分布时的熟化规律相较均匀分布有明显差别[23],因此选取了两种不同气泡群初始分布工况(工况1#、2#)进行分析(表1).与工况1#相比,工况2#仅改变第3 层气泡群初始半径.同时,孔隙数的选取对平均毛细力、饱和度等连续尺度等效参数的获取具有显著影响,为了分析孔隙数对熟化过程的影响,本文构建了孔隙数分别为325 个(工况1#)和10800 个(工况3#)两种多孔介质,具体参数见表1.工况3#气泡群初始分布与工况1#相同.模拟在常温常压条件下进行,表2 整理了气泡熟化模拟时选用的参数.

表1 模拟工况参数Table 1.Simulation parameters of three conditions.

表2 四孔隙及多孔隙结构气泡熟化模拟参数Table 2.Simulation parameters of four bubble and muti bubble ripening system.

3 实验方法

本实验选用硅基微流体芯片,以去离子水作为液相,CO2作为气相.芯片分别对硅基底进行两次刻蚀制备出孔隙与喉道图案,得到具有不同深度流道的2.5D 结构,能对芯片内的气泡进行夹断,使每个孔隙里只有一个气泡[17].芯片观察部分为四孔隙结构,具体结构如图5 所示,其中孔隙深度为30 µm,喉道深度为10 µm.本文采用气泡熟化可视化实验装置对气泡在四孔隙结构内熟化过程进行研究,具体的实验装置与方法见参考文献[29].

图5 微流控芯片内部结构Fig.5.Internal structure of microfluidic chip.

4 讨论部分

4.1 模型验证

对四孔隙结构气泡熟化系统进行实验及模拟研究,结果如图6 所示.熟化过程中,虽然气泡1 的半径小于气泡3,但熟化结束后气泡3 消失而气泡1 并未消失.这是由于气泡1 受到了气泡2 的质量传输,而气泡3 周围存在半径更大的气泡4,使得气泡3 向气泡4 传质,最终导致上述现象的发生.可见气泡的初始分布不同,会导致不同熟化过程的发生.

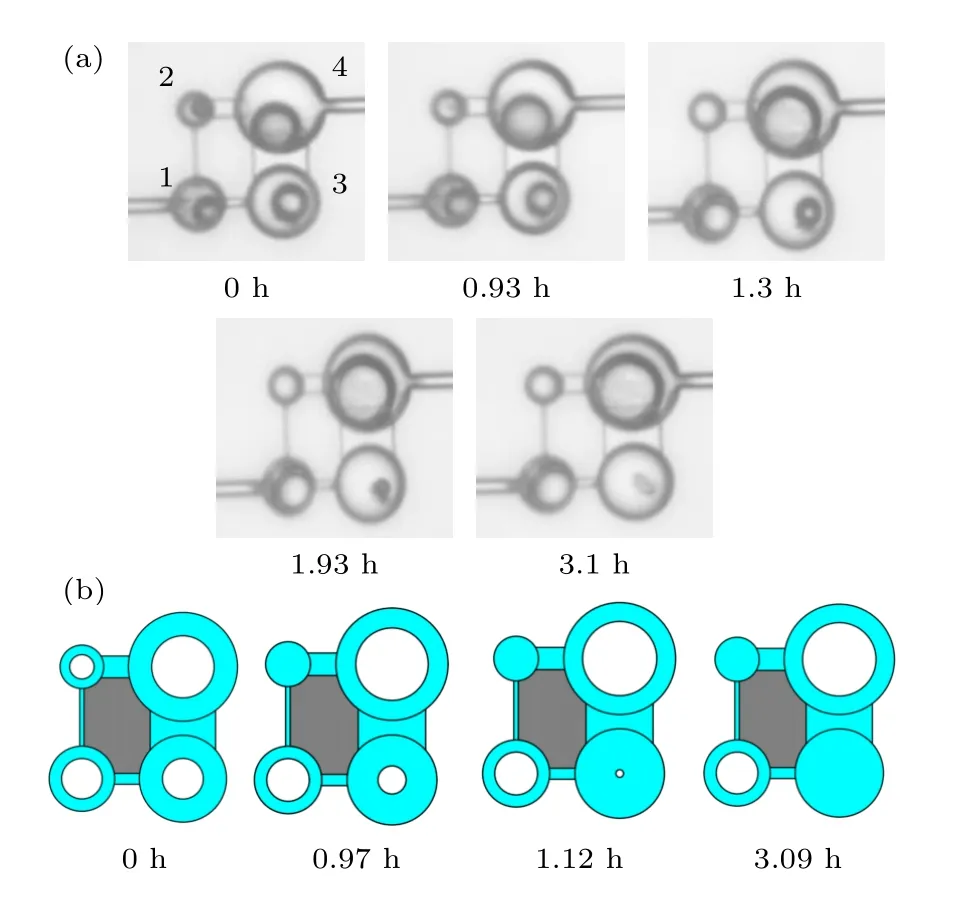
图6 四孔隙结构气泡熟化过程 (a)实验过程;(b)模拟过程Fig.6.Four bubble ripening system: (a) Experiments process;(b) simulations process.

图7 为四孔隙结构熟化过程中气泡半径变化的模拟和实验结果对比,模拟和实验结果符合较好.在熟化时间上,除气泡3 存在差别,其余气泡达到稳定的模拟时间与实验较为吻合.造成这种差别的原因在于模拟过程中气泡位置始终位于孔体正中心,而在实际实验中,气泡的位置会与孔体正中心存在一定偏差.随着熟化的进行,模拟和实验结果偏差会随之变大.

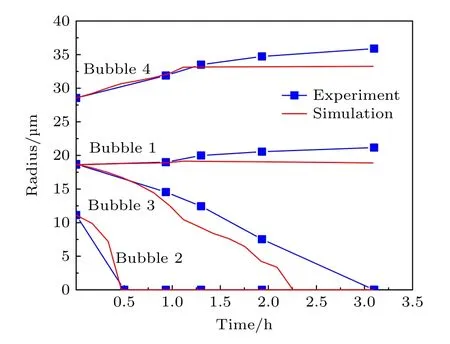
图7 四孔隙结构气泡半径随时间变化Fig.7.Evolution of curvature radius in four bubble ripening system.

4.2 气泡初始分布对熟化过程影响

由于工况1#各层孔隙结构和气泡初始半径均相同,因此三维空间内不同深度方向之间不存在传质,故选用单层二维平面数据进行讨论.工况1#中气泡熟化过程如图8 所示.观察图8 发现:1)由于小孔隙区域气泡半径小,毛细压力大,因此在熟化初期小孔隙区域气泡半径显著减小,气体从该区域传输至大孔隙区域;2)熟化过程中,大、小孔隙区域气泡的消失顺序呈现间隔性,如熟化进行至14 h 时,小孔隙区域残留气泡呈现规则性的间隔分布,4.4×1018h 的大孔隙区域残留气泡分布也呈现相同规律;3)在熟化末期,小孔区域残留气泡集中在中间区域,即靠近及远离大孔隙区域的气泡最先消失,该现象对连续尺度模型的建立具有指导意义,目前文献认为小孔隙区域气泡消失的顺序应从靠近大孔隙区域开始逐列向远离该区域的方向推进.

图8 工况1#模拟结果 (a)气泡演化过程,其中白色区域为CO2 气泡,蓝色区域为去离子水,灰色区域为硅颗粒;(b) CO2 气泡曲率半径变化图Fig.8.Simulation results of condition 1#: (a) Bubble evolution process,where the white regions are CO2 bubble,blue regions are filled with DI water,and the gray regions are silicon grains;(b) curvature radius variation diagram of each CO2 bubble.

为了解释上述现象,采用一维孔隙结构的气泡熟化过程进行说明(图9).一维孔隙结构由3 个小孔体和1 个大孔体构成,每个孔体间通过喉道相连.小孔体内的气泡大小相同,且小于大孔体内气泡.气泡间传质受毛细力决定的浓度梯度与扩散距离影响.因此,熟化开始时,与大气泡4 毗邻的小气泡3 最先发生熟化,导致气泡3 半径减小,此时气泡4、气泡3 和气泡2 的半径大小关系为R4＞R2＞R3,故气泡3 同时向气泡4 和气泡2 传质(见图9 箭头方向).气泡2 获得传质后半径增大,使得R2＞R1,引起气泡1 向气泡2 传质.上述传质现象的存在,使得气泡发生规则性的间隔消失.在多孔隙结构(图8(a))中,这种间隔变化使小孔隙区域内气泡质量往大孔隙区域传输的同时,还会往中间区域积累,因此在小孔隙区域内位于中间列的气泡最慢消失.

图9 一维孔隙结构气泡熟化过程Fig.9.Bubble evolution process of one-dimensional structure.

工况2#中,由于孔体结构和气泡初始尺寸的对称性,第1 层和第5 层的熟化情况相同,第2 层与第4 层的熟化情况相同.工况2#中气泡熟化过程如图10 所示.观察图10 发现,由于气泡非均匀分布,熟化过程与工况1#存在以下区别: 1)工况1#中由于气泡均匀分布,不存在向不同深度的中间层区域传质的现象,而工况2#中气泡从小孔隙区域传输至大孔隙区域的同时,大、小孔隙区域也会各自向自身区域的大气泡区域传质,因此整个熟化过程会向中间层区域逐层推进;2)如图10(b),(d)所示,由于气泡初始分布的差异,小孔隙区域内气泡熟化进行更快,整个孔隙空间内所有气泡完成熟化的时间为1.7×1018h,与工况1#中完成熟化的时间量级上较为相近.进一步证明了气泡熟化是一个长时间尺度的过程,CO2地质封存中达到平衡需要数百万年时间[30],时间尺度的研究可以确定封存过程中CO2的长期储存能力,评估地质封存系统的稳定性和长期效果;3)对比工况1# (图8(b))与工况2# (图10(b),(d),(f))中气泡曲率半径变化发现,由于工况2#中自身熟化现象更显著,在熟化末期大孔隙区域内大部分气泡都会充满孔隙.该模型可以模拟CO2气泡在地下储层中的传输和分布过程,确定潜在的CO2泄漏路径和风险,为CO2地质封存技术提供重要的指导意义.

图10 工况2#模拟结果 (a)第1 层和第5 层气泡演化过程;(b)第1 层和第5 层CO2 气泡曲率半径变化;(c)第2 层和第4 层气泡演化过程;(d)第2 层和第4 层CO2 气泡曲率半径变化;(e)第3 层气泡演化过程;(f)第3 层CO2 气泡曲率半径变化Fig.10.Simulation results of condition 2#: (a) Bubble evolution process in layers 1 and 5;(b) curvature radius variation of each CO2 bubble in layers 1 and 5;(c) bubble evolution process in layers 2 and 4;(d) curvature radius variation of each CO2 bubble in layers 2 and 4;(e) bubble evolution process in layer 3;(f) curvature radius variation of each CO2 bubble in layer 3.

4.3 孔隙数对熟化过程影响

熟化过程连续尺度模型参数的构建依赖于孔隙尺度熟化特性的研究,可基于孔隙尺度模拟获得连续尺度等效参数,如平均毛细力、饱和度等参数.孔隙尺度下多孔介质孔隙数的选取对连续尺度等效参数的获取具有显著影响.为此,本文对工况1#和工况3#熟化过程中CO2气泡受到的毛细力与饱和度变化进行统计.熟化过程中气泡受到的平均毛细力如图11(a)所示,当孔隙数较少时,个别气泡半径的突变也会对整个孔隙空间产生较大的影响,使毛细力曲线走势振荡;当孔隙数较多时,毛细力呈下降趋势,曲线波动较少.熟化过程中饱和度随时间的变化如图11(b)所示,熟化初期小孔隙区域内的气泡向大孔隙区域传质,导致小孔隙区域饱和度持续下降,而在熟化后期大孔隙区域内的气泡之间也会发生熟化使大孔隙区域整体饱和度降低.孔隙数的增加提供了更多的气体扩散路径,使大孔隙区域内气泡自身熟化的情况更复杂.

图11 CO2 气泡各参数变化图 (a)毛细力;(b) CO2 饱和度Fig.11.Variation diagram of CO2 bubble parameters: (a) Capillary pressure;(b) CO2 saturation.

在构建连续尺度熟化模型时,毛细力与饱和度关系式的选取直接影响熟化模型精度[31].目前国内外学者在建立多孔介质内CO2熟化连续尺度模型时,认为熟化过程中CO2气泡毛细力与饱和度呈线性关系,如Li 等[18]提出的连续尺度数值模型中选用了“Pc=a+bSg”的毛细力模型.本文分别对两种工况模拟过程中气泡毛细力与饱和度进行统计,其变化关系如图12 所示,两种工况下大、小孔隙区域内的毛细力与饱和度的变化均呈现非线性关系.对比图12(a)和图12(b)发现,当孔隙数增加时,大孔隙区域和小孔隙区域内毛细力与饱和度关系的规律性显著提升.这是由于熟化过程中气泡的变化情况非常复杂,气泡所受的毛细力与饱和度都经历了大幅改变.工况3#中毛细力与饱和度关系的变化具有更明显的规律性,故对该工况下的数据点进行非线性拟合,得到小孔隙区域内毛细力与饱和度的关系式为大孔隙区域内毛细力与饱和度的关系式为Pc=.研究毛细力和饱和度的关系,可以提升连续尺度熟化模型的可靠性和预测能力,为CO2地质封存过程提供指导和决策支持.

图12 气泡毛细力与CO2 饱和度关系对比图 (a)小孔隙区域;(b)大孔隙区域Fig.12.Comparison of capillary pressure with CO2 saturation curves: (a) Small pore region;(b) large pore region.