混沌光注入半导体激光器中极端事件的演变*
2023-09-06戈杉杉王腾午戈静怡周沛2李念强2
戈杉杉 王腾午 戈静怡 周沛2)† 李念强2)‡
1) (苏州大学,光电科学与工程学院,苏州纳米科技协同创新中心,苏州 215006)
2) (苏州大学,教育部/江苏省现代光学技术重点实验室,江苏省先进光学制造技术重点实验室,苏州 215006)
基于相位共轭光反馈混沌激光系统(主激光器)产生的极端事件,研究了将其输出注入到一个自由运行的半导体激光器(从激光器)的演化情况.通过注入参数空间中极端事件相对数量的二维统计图分析注入参数对极端事件产生的影响,发现在主从激光器混沌输出高相关性参数区域,从激光器中的极端事件的相对数量趋向于一个接近主激光器中极端事件相对数量的稳定值;在某些特定的弱相关区域,从激光器中的极端事件的相对数量趋向于增加.研究结果证明了通过光注入控制极端事件的可能性,有利于优化混沌激光系统性能或拓展其应用场景.
1 引言
具有高影响、异常量级、不可预测性和偏离高斯统计特点的异常波(rogue wave,RW)最初是在海洋学中被提出的,用来描述罕见的高振幅海浪,在自然、技术和社会环境系统中受到了极大的关注[1].由于高振幅RW 在现实场景中会造成破坏性影响,因此研究RW 的产生与形成机制是非常有意义的.然而,RW 自身的稀有性以及实验实施的困难性一直限制着人们理解RW 形成机理.2007 年,Solli 等[2]将光场在光纤中的传播与海洋中RW 的出现进行类比,引入了光学RW 的概念,即极端事件(extreme event,EE).得益于快速的动态特性,光纤传输系统成为检测EE 的最佳测试平台之一.此后,EE 的研究进入了一个繁荣期,人们提出了不同的光学系统来分析EE 的产生和演变.线性系统是研究EE最广泛的系统之一,例如玻璃纤维[3]、随机介质[4]和线性干涉模型[5]中的线性光传播.除了上述线性系统,人们还致力于研究产生EE 的非线性系统,如微结构光纤[2]和锥形渐变折射率非线性光纤[6].在这些非线性系统中,主要是利用非线性薛定谔方程来研究EE 的形成机理.近年来,确定性非线性系统,如半导体激光器,被广泛用于研究EE 的产生,这极大地加速了EE 相关研究的发展.
一方面,具有丰富动力学特性的半导体激光器为理解和预测EE 提供了一个廉价和可控的平台.另一方面,EE 的行为是理解不同激光系统中基础物理的有力工具.目前,已经有很多研究集中在受到光注入以及光反馈的半导体激光器中[7−20].例如,Bonatto 等[19]实验观察到光注入半导体激光器输出强度中出现了罕见的巨脉冲,脉冲幅度的长尾概率分布符合EE 的特征.利用最大李雅普诺夫指数(largest Lyapunov exponents,LLE),发现EE只出现在混沌区域,表明这种EE 源于确定性非线性.在后来的工作中,结合相空间轨迹图,他们进一步证明了确定性EE 是由一个类似混沌危机的过程产生的[9].物理机制的理解为提高注入半导体激光器的性能提供了一条途径,例如,EE 可以在较长的时间内被预测,并且可以随着噪声的变化而增加或抑制其产生概率.此外,时滞非线性光学中也研究了EE 的形成[7,8,12,14,16].例如,Dal Bosco 等[7]报道了一个光学时滞系统的脉动动力学中的极端事件,研究了反馈强度对极端事件性质的影响.Reinoso 等[8]对具有光反馈的半导体激光器在短腔区产生的脉冲进行了数值研究,发现对于某些参数,偶尔会产生高到足以被认为是极端事件的脉冲.2015 年,Mercier 等[12]在一个相位共轭反馈的激光二极管中观察到与异常涌浪具有相似统计特性的极强脉冲,证实了EE 产生于自脉动解的一系列分岔,即外腔模式.
尽管具有光注入或光反馈的半导体激光器中EE 的研究已经得到了相当多的关注,但是对于两者相结合的系统中EE 的产生与调控仍然缺乏深入和全面的研究.一个有趣的问题是,具有EE 的光反馈主激光器(master laser,ML)的混沌输出注入到一个从激光器(slave laser,SL)中,是否能够触发、增强或抑制从激光器中EE 的产生.近期,Huang 等[17]通过实验研究了受到混沌光注入的SL中EE 的演变,其中ML 受到传统光反馈(conventional optical feedback,COF).他们揭示了注入参数对SL 中EE 出现的重要性,在所选择的注入参数范围内,可显著提高EE 的出现概率,SL 中EE 的出现与注入锁定机制相关联.相位共轭反馈(phaseconjugate feedback,PCF)是另一种类型的光反馈,与COF 相似,在适当的工作条件下,PCF 可以诱导出混沌动力学[21].然而,相比于COF,对于相同的系统固有参数和操作参数(延迟、泵浦电流和反馈强度),PCF 系统产生的混沌带宽更大,光谱平坦度更优以及复杂性更高[22],这些优越特性增加了使用PCF 代替COF 的内在优势,即反馈场的自对准和高反馈耦合效率.相位共轭反射镜也很容易实现,例如,利用自泵浦的、适当对齐的光折变晶体的内部反射率[23].因此,本文致力于利用PCF代替COF,进一步研究PCF 与光注入相结合的混沌光注入系统中EE 的产生与调控.基于此,对基于PCF 的混沌光注入系统(chaotic optical injection system based on PCF,COIS-PCF)进行了数值模拟,研究输出中EE 的演变情况,通过讨论不同注入参数的选择对EE 出现的作用,发现当主从系统的互相关系数(cross-correlation coefficient,CC)进入部分区间内(如0—0.2,0.4—0.6),SL 中会对EE出现产生明显的增强作用.此外,还发现调节反馈强度和ML 的泵浦电流大小也会对系统中EE 的出现产生影响.
2 理论模型
基于Lang-Kobayashi 模型提出了下列的方程用于描述当前研究的系统[24−26],其中ML 方程为
式中,下标M 和S 分别代表主激光器ML 和从激光器SL;E(t)和N(t)表示慢变电场和载流子密度;G为光增益;g为差分增益系数;ε为增益饱和系数;α为线宽增强因子;N0为透明载流子数;τp为有源区内光子的寿命;τe为有源区内载流子的寿命;J为泵浦电流(Jth为阈值电流);q为电子电荷;ϕPCM为相位共轭反射镜引起的相移(不失一般性,假定ϕPCM=0);kf为反馈强度;τM为主激光器中的反馈时延;fML为主激光器的中心频率;kinj为注入强度;τc为注入时延(不失一般性,假定τc=0);Δf为主从激光器频率失谐(Δf=ΔfML– ΔfSL,其中fSL为从激光器的中心频率).
这里采用四阶龙格-库塔算法来解方程(1)—方程(6),选取步长h=1 ps,仿真时长为11 µs,选取后10 µs 计算EE 的相对数量.激光器的参数取值为[12,24−26]:
为了描述两个激光器之间的相关性,计算了互相关系数CC,表达式如下[27−29]:
其中I(t) 表示强度时间序列;下标M 和S 分别表示ML 和SL;Δt为时间偏移;〈·〉 为时间平均值.CC值越大,两激光器输出之间的相关性越高.特别地,值为1 对应于完全同步,而值为0 表示没有相关性.
这里定义事件为序列中的局部极大值,而为了将EE 与所有其他事件区分开来,采用了一种常见的标准异常指数(abnormality index,AI),该指数在以往的研究中被广泛使用[12,16,30−32].一个事件n的AI 被定义为
其中Hfn为事件n的峰值高度与该序列所有事件平均高度之差,而H1/3为Hfn中最高三分之一事件峰值的平均值.如果一个事件n的异常指数满足AIn≥2,该事件即为极端事件.此外,EE 的相对数量表示强度时间序列中的EE 占所有峰值的比例.
3 结果与讨论
首先,研究了作为混沌注入信号源ML 中的时序.图1 为ML 的输出时序和峰值强度的概率密度函 数(probability density function,PDF).结合图1 中PDF 呈现的长尾特征和ML 的输出时序,很容易知道ML 处于混沌状态.经计算,在反馈强度kf=9 ns–1时,ML 中EE 的相对数量为1.84%,当反馈强度增加到kf=15 ns–1,EE 相对数量增加到3.13%,再进一步增加反馈强度到kf=30 ns–1,EE 相对数量减小为2.29%.事实上,增加反馈强度会使带有PCF 的半导体激光器振荡在一个或几个谐波频率越来越高的外腔模式之间[14],正如图1(a1)—(c1)所示,在10 ns 的时间范围内,随着反馈强度增加,脉冲数量逐渐增多.当反馈强度从9 ns–1增加到15 ns–1时,由于反馈强度的增加,激光器可能工作在更高阶的外腔模式下,于是在固定的时间间隔内更多的高强度脉冲出现,EE 的相对数量增加.而反馈强度从15 ns–1增加到30 ns–1时,由于更多强度低于EE 阈值的脉冲产生,因而EE 的相对数量减小.这些分析表明反馈强度可显著影响EE 的产生,类似的现象在带有COF 的垂直腔面发射激光器(vertical-cavity surface-emitting laser,VCSEL)中也被观察到[30].

图1 ML 的时序图和峰值强度的统计分布图(红色虚线和竖线代表极端事件的阈值AI=2) (a) kf =9 ns–1;(b) kf =15 ns–1;(c) kf =30 ns–1Fig.1.Time series and statistical distributions of peak intensity in ML (Red dashed lines and vertical lines represent the threshold of EEs,AI=2): (a) kf =9 ns–1;(b) kf =15 ns–1;(c) kf =30 ns–1.
接着,分析SL 输出中的EE 情况.这里选择了一个适中的注入强度kinj=100 ns–1和反馈强度kf=15 ns–1,展示了三种频率失谐下的SL 中的时序和对应的峰值强度的PDF.图2(a)为频率失谐为正失谐Δf=15 GHz 时的情况,此时在10 μs的时序中EE 的相对数量为2.12%;在图2(b)所示的零失谐情形中,EE 的相对数量为4.71%;而图2(c)对应负频率失谐Δf=–20 GHz,通过计算得到EE 的相对数量为1.29%.相比于零失谐情形,在正失谐的情形中,可以在固定的时间间隔内观察到更多的高强度振荡脉冲,这导致EE 的阈值显著变高,一些原来刚高于零失谐阈值的EE,由于新阈值变高不再是EE,因而EE 的相对数量较零失谐情形下有所降低.同样,负失谐情形中,也可以在固定的时间间隔内观察到更多的振荡脉冲,但是出现的主要是强度不太大的脉冲,很少有高强度脉冲出现,甚至零失谐中的部分高强度脉冲被抑制,导致EE 的阈值和零失谐阈值相比几乎不变,同时由于更多低于阈值的脉冲的出现,这种情形下EE 的相对数量低于零失谐情形.由以上结果可以知道,频率失谐也可以影响EE 的产生.

图2 kf=15 ns–1,kinj =100 ns–1 时,SL 的时序图和峰值强度的统计分布图 (红色虚线和竖线代表极端事件的阈值AI=2) (a) Δf=15 GHz;(b) Δf=0 GHz;(c) Δf=–20 GHzFig.2.Time series and statistical distributions of peak intensity in SL at kf =15 ns–1 and kinj =100 ns–1 (Red dashed lines and vertical lines represent the threshold of EEs,AI=2): (a) Δf=15 GHz;(b) Δf=0 GHz;(c) Δf=–20 GHz.
下面研究注入强度对SL 中EEs 的影响.图3展示了在 Δf ∈[-20,15]GHz,kf∈[9,30]ns-1条件下,EE 相对数量随注入强度kinj的变化情况.在零失谐情形下,SL 中EE 的相对数量几乎在整个参数范围内都是高于ML 中EE 的相对数量,表现为增强作用.对于负失谐的情形,即Δf=–20 GHz时,当注入强度约小于150 ns–1时,SL 中EE 相对数量低于ML,表现为抑制作用,超过150 ns–1,SL中EE 相对数量主要表现为增强作用.对于Δf=15 GHz 正失谐情形,EE 的相对数量会随着注入强度的增大先增大后减小,随着注入强度的进一步增大,EE 的相对数量会再次增加并逐渐达到饱和,在整个注入强度的参数范围内,EE 的相对数量会在一些区域被抑制,另外一些区域被增强,当反馈强度达到30 ns–1,EE 相对数量得到增强的区域最为广泛.通过比较图3(a)—(c),发现随着反馈强度增加,零失谐和负失谐情形中,SL 中EE 相对数量得到增强的参数范围几乎不发生改变,而在正失谐情形中的EE 相对数量得到增强的参数范围先缩小,后扩大.因而可知: 注入强度对SL 中EE 的相对数量的增强、抑制同样也很关键,同时注入强度的作用还会受到反馈强度的影响.

图3 SL 中EE 的相对数量随着注入强度变化情况(灰色虚线代表ML 中EE 的相对 数量) (a) kf =9 ns–1;(b) kf =15 ns–1;(c) kf =30 ns–1Fig.3.Relative number of EEs versus injection strength(Gray dashed lines represent the relative number of EEs in ML): (a) kf =9 ns–1;(b) kf =15 ns–1;(c) kf =30 ns–1.
为了全面研究SL 中EE 相对数量随注入参数的变化情况,图4(a1)—(c1)展示了不同反馈强度下SL 中EE 相对数量随注入参数 Δf,kinj变化的二维图.图4(a1)—(c1) ML 中的EE 相对数量分别为1.84%,3.13%,2.29%,图中的蓝色区域表示SL 中EE 相对数量受到抑制,黄绿色区域表明SL 中EE 的相对数量接近于ML 中EE 的相对数量,深红色区域对应EE 相对数量得到增强.考虑到SL 中EE 的发生可能与ML 和SL 之间的相关性有关,还展示了注入参数空间中对应的CC 的二维映射图,如图4(a2)—(c2)通过三种反馈强度的比较可以发现,随着反馈强度的增加,用暗红色标记的高相关性的区域在选定的参数空间中越来越小.值得注意的是,在该区域内反馈强度为9 ns–1时,SL 中EE 的相对数量接近于ML 中EE 的相对数量.然而,随着反馈强度的增大,例如,反馈强度为15 ns–1以及30 ns–1时,高相关性区域内EE的相对数量显著增加.有趣的是,在该区域之外,当CC 在0.4—0.6,对应图4(a2)—(c2)中的黄绿色区域时,相应的参数区域在图4(a1)—(c1)均被标记了暗红色,也就是说,在三种不同的反馈强度下,正负失谐部分都存在EE 相对数量得到明显增强的区域.进一步观察,还发现该增强区有逐渐扩大的趋势,同时负失谐增强区始终大于正失谐增强区,这揭示了非零线宽增强因子带来的关于零失谐的不对称行为[2].此外,在图4(a2)—(c2)中的蓝色区域,即CC 低于0.2 时,在对应的图4(a1)—(c1)中正失谐部分还有一块暗红色增强区域,该增强区域的产生类似于已经报道的传统光反馈形成的混沌光注入系统 (chaotic optical injection system based on COF,COIS-COF)[17].上述讨论表明: 在ML和SL 相关性不高的特定参数区域中,SL 中EE 相对数量可能会被增强,尤其在CC 处于0.4—0.6时,被增强的概率很大,当CC 低于0.2 时,正失谐参数下EE 的产生也可能被增强.而反馈强度的增大,一方面可以扩大高相关系数外的增强区域,另一方面可以增加高相关性区域内的EE 相对数量.
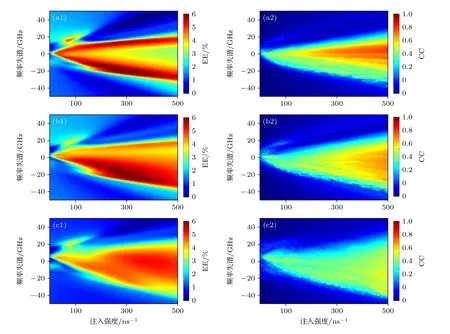
图4 COIS-PCF 中EE 相对数量在注入参数空间内的二维图(a1)—(c1)以及对应的主从激光器互相关系数的二维映射图(a2)—(c2) (a) kf =9 ns–1;(b) kf =15 ns–1;(c) kf =30 ns–1Fig.4.Maps of relative number of EEs generated from the COIS-PCF in the injection-parameter space (a1)–(c1) and corresponding CC between the ML and SL (a2)–(c2): (a) kf =9 ns–1;(b) kf =15 ns–1;(c) kf =30 ns–1.
下面考虑在COIS-PCF 中调节ML 的泵浦电流JM对EE 产生的影响.在讨论SL 之前先讨论ML中产生的EE.为了便于讨论,固定了ML 的反馈强度kf=30 ns–1和阈值电流Jth=14.7 mA,只调节ML 的泵浦电流.通过观察图5 中展示的不同泵浦电流下ML 中的时序和对应的峰值强度的PDF,很容易知道ML 输出均处于混沌状态,都有少量EE产生,经计算其相对数量分别为2.29%,1.90%,1.30%,1.36%.对于图5(a)—(c),尽管随着泵浦电流变大,有高强度的脉冲出现,但信号时序的平均强度增加使得EE 的阈值变高,导致EE 的相对数量降低.而在图5(c),(d)中,泵浦电流进一步增加,由于激发强度较小的脉冲数量变少,后者中EE 相对数量反而略高于前者.由此可知,ML 的泵浦电流JM同样影响着EE 的产生.

图5 kf =30 ns–1 时,ML 的时序图和峰值强度的统计分布图 (红色虚线代表极端事件的阈值AI=2) (a) JM=1.05Jth;(b) JM=1.30Jth;(c) JM=1.50Jth;(d) JM=2.00JthFig.5.Time series and statistical distributions of peak intensity in ML at kf =30 ns–1 (Red dashed lines and vertical lines represent the threshold of EEs,AI=2): (a) JM=1.05Jth;(b) JM=1.30Jth;(c) JM=1.50Jth;(d) JM=2.00Jth.
接着我们进一步研究JM对SL 中EE 的影响.图6(a1)—(d1)为JM/Jth∈[1.05,2],kf=30 ns–1条件下,SL 中产生EE 的相对数量随注入参数Δf和kinj变化的二维图,其中ML 的EE 相对数量分别为2.29%,1.90%,1.30%,1.36%,对应图中淡蓝色区域.同样地,图6(a2)—(d2)也展示了注入参数空间中对应的CC 的二维映射图.通过对比4 种JM的映射图,发现随着JM不断增加,参数空间中用暗红色标记的ML,SL 高相关性区域不断扩大,而在高相关性区域参数下SL 中产生EE 的相对数量均趋向于一个接近ML 中EE 相对数量的稳定值,并且类似于图4,主从激光器CC 在0.4—0.6 的参数区域也出现了红黄色的增强区域.值得注意的是,在图6(a2)中CC 低于0.2 的蓝色区域对应的参数下,尽管在正失谐部分有EE 增强区,却并未在负失谐部分触发EE 增强区,但当JM不断增加,如图6(b1)—(d1)所示,负失谐部分逐渐产生了一块不断增大的红黄色增强区.于是可以得出结论: ML 的泵浦电流JM增加会导致参数空间中高相关性区域的扩大,同时促进低相关性区域中EE 负失谐增强区的产生与增大.
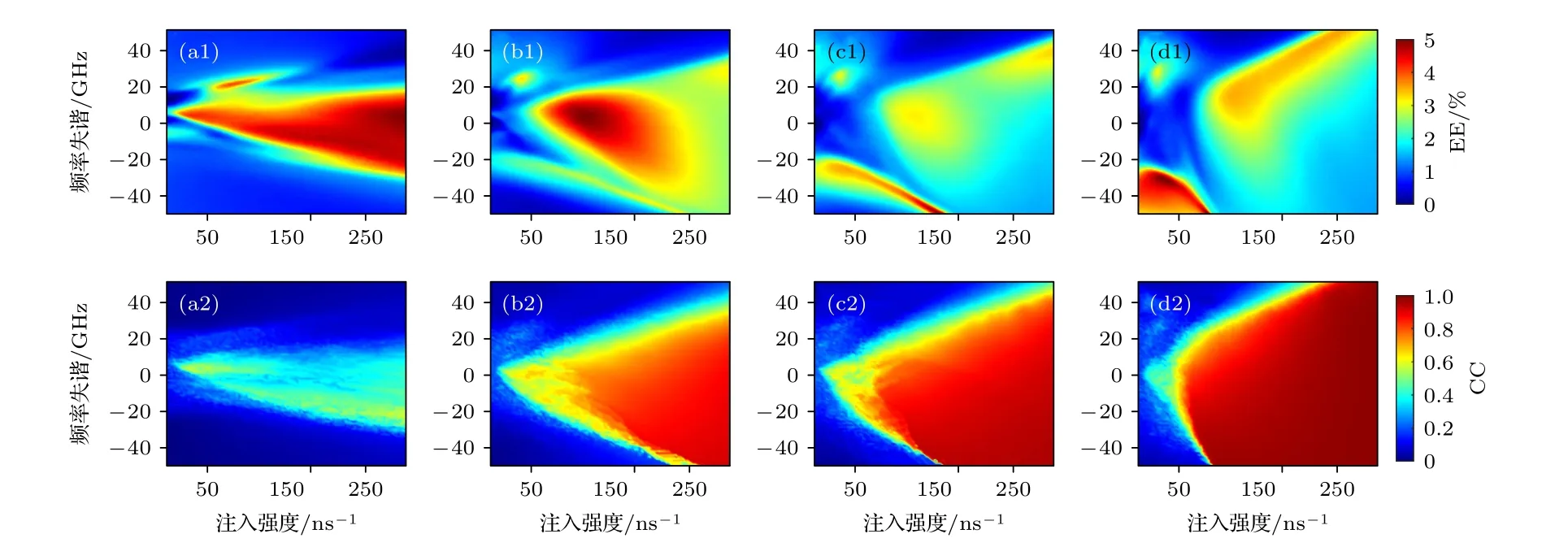
图6 COIS-PCF 中EE 相对数量在注入参数空间内的二维图(a1)—(d1)以及对应的主从激光器互相关系数(a2)—(d2) (a) JM=1.05Jth;(b) JM=1.30Jth;(c) JM=1.50Jth;(d) JM=2.00JthFig.6.Maps of relative number of EEs generated from the COIS-PCF in the injection-parameter space (a1)–(d1) and corresponding CC between the ML and SL (a2)–(d2): (a) JM=1.05Jth;(b) JM=1.30Jth;(c) JM=1.50Jth;(d) JM=2.00Jth.
4 结论
本文对COIS-PCF 系统进行仿真,数值分析了混沌输出中EE 的特性.通过观察可知在研究的参数范围内,作为注入源的ML 和被注入的SL 始终工作在混沌状态,输出中均有EE 的产生.接着讨论了注入参数对输出中EE 相对数量的影响,结果表明: 在高相关性参数区域,SL 中EE 的相对数量趋向于一个接近ML 中EE 相对数量的稳定值;在CC 处于0.4—0.6 的参数区域,有很大概率会出现EE 的增强区;而CC 低于0.2 的区域仅在正失谐部分有增强区的出现.进一步,发现对于相同的注入参数范围,反馈强度的增加不仅会扩大增强参数区域,还会增加高相关性区域内的EE 相对数量.此外,在一个适当的反馈强度条件下,不断增加ML 的泵浦电流并进行比较,发现ML 泵浦电流的增大会导致主从系统有更大的锁定参数范围,还会在负失谐部分产生一个不断扩大的EE 增强区.
