质子碰撞硼原子非辐射的电荷转移过程*

朱宇豪 袁翔 吴勇 王建国

1) (西安建筑科技大学理学院,西安 710055)

2) (北京应用物理与计算数学研究所,计算物理重点实验室,北京 100084)

重粒子碰撞中的电子转移涉及复杂的电子关联机制,极大地影响等离子体中电荷态平衡,也是X 射线的辐射的重要来源之一.电子转移截面与速率系数是国防工业发展核聚变等离子体所需要的重要原子参数.基于全量子的非辐射分子轨道密耦合方法,系统研究了质子碰撞硼原子在 10-3—103 eV/u 能量区间内的硼原子电子转移过程.计算采用多参考组态方法得到总共15 个电子转移、激发以及弹性散射的通道,每个通道对应的分子态能量得到了与实验符合较好的结果.分子态的绝热势能曲线间的避免交叉现象明显,构成了电子转移的主要途径.计算发现,质子碰撞硼原子过程中2s 轨道的电子转移是占主导地位,2p 轨道的电子转移贡献较小.在低能区,电子转移截面出现了明显的量子共振现象,这些共振主要来源于不同能量通道的耦合.此外,还计算了不同温度下的质子碰撞硼原子的电子转移速率,该速率可为复杂等离子体环境的模拟诊断提供重要的原子参数支持.

1 引言

重粒子碰撞中的电子转移涉及多电荷动力学以及多体相互作用等复杂物理过程,因为其在天体和等离子体物理中有非常重要的应用,吸引了广泛的理论和实验研究[1].在磁性约束核聚变中,质子对电子的俘获极大影响了整个系统的电荷态平衡以及等离子体冷却过程.电荷态平衡是诊断复杂等离子体系统基础的指标,从中可以获得元素丰度、电荷密度等物理信息[2].在天体环境中,X 射线谱是识别天体可观测气体元素重要的手段之一,并且各类元素的X 射线辐射都与电子转移有密切的关系.特别对于内壳层电子的转移过程,是原子系统X 射线辐射的重要来源[3].所以,为了模拟上述X 射线谱和等离子体中电荷态平衡等过程,获得重粒子碰撞中的电子转移态选择截面和总截面是很有意义的.那么,重粒子碰撞的电子转移截面等相关信息已经成为不可或缺的原子参数,为国防工业发展核聚变技术,以及为等离子体物理等学科中演化模拟复杂等离子体系统提供强有力的原子参数支持[4,5].

近年来,对重粒子碰撞的理论研究也迅猛发展,在不同的入射能区,理论计算可以做到与实验测量符合较为精确的结果.如在中高能区的原子轨道密耦合方法[6−9],能够精确计算重粒子碰撞的电子激发和转移的态选择截面以及总截面.因为其只对电子做全量子化的处理,而原子核依然采用经典力学的运动方式,所以该方法为半经典的理论方法.在低能入射区,量子效应更加明显,需要采用全量子的碰撞方法才能考虑足够的物理信息得到精确的电子转移截面.目前,较为常见的全量子的理论方法是非辐射分子轨道密耦合方法,Liu 等[6,10−14]基于此方法成功计算出了He,Li 以及Be 等原子系统的电子转移截面,并与相关精密实验测量结果符合得较好.全量子的分子轨道方法,因为分子轨道模型可以准确描述较低能区的散射态波函数,并能够有效处理各个分子轨道之间的耦合,其在计算低能区对电子转移的截面计算属于国内外公认的最高精度方法.当然,分子轨道方法的精确度主要取决于分子态能量,即分子电子态结构的精度.这要求在计算分子结构时,需考虑足够大的组态空间和足够多的电子组态,充分考虑电子关联对分子结构的影响[14].

在实验研究方面,重粒子碰撞是阐明量子多体关联,揭示靶粒子内部结构信息的重要科学手段.国内外已经开展了数十年的重粒子碰撞实验,诸多质子或氢原子与重元素原子不同价态系统的碰撞实验都相继展开.比如,Bruhns 等[15,16]使用合并束技术研究了氢原子与Si3+离子在地能区碰撞的电子转移过程,并精密测量了电子转移截面.Gieler等[17,18]研究了质子碰撞K 原子的低能区电子转移总截面,其中Gieler 等[17]的碰撞能区在 1 —10 keV/u,Ebel 等[18]的研究能区在 0 .1—1.0 keV/u .虽然诸多原子系统与质子碰撞中电子转移过程被实验陆续研究[19-22],但是据目前调研所知,还从未开展对B原子的实验研究,然而B 原子在天体中也具有较高丰度,因此迫切需要B 原子参数.此外,B 原子与质子的碰撞过程也是研究多体相互作用系统的良好平台,其中涉及多体相互作用的电子转移机制还没有被发掘.因此,质子碰撞B 原子的理论研究,不仅可以更深一步了解其电子转移机制,还能认识碰撞过程中多电子关联效应.

本文基于全量子非辐射的分子轨道密耦合方法,系统研究大范围碰撞能区内质子碰撞B 原子电子转移过程.考虑足够多的电子态,以确保整个计算中通道的收敛性.第2 节详细阐述计算的理论方法;第3 节展示计算结果并讨论相关电子转移的物理机制;第4 节对研究工作做简短的总结.

2 理论方法

2.1 分子电子态结构计算

分子电子态结构的计算,采用Buenker 等[23−25]提出的Table-direct CI 结合多参考单双激发组态相互作用方法(MRDCI).该方法在自洽场计算(HF-SCF)之后,能基于单双激发的参考组态,可以最优化选取占比重要的组态,缩小了组态空间,且可以保证精度.则说明MRDCI 可以快速优化组态构成,得到精确的电子态波函数,其具体计算公式为

其中,ψα(PJM) 是电子态波函数,ϕr(PJM) 为参考组态考虑单双激发后的优化的组态波函数,cr(r)是混合系数.实际计算中,通常选取对内、外壳层和极化作用考虑较好的芯-价关联极化的多Zeta 基组,加入弥散基来弥补由于高激发态离核较远导致电子云分布较大的影响.做完自洽场计算后,构建组态空间,对于选定的参考组态进行单双电子激发,但是这样经常会导致组态空间偏大,因此可以通过设定阈值、结合“有效势场”控制活动电子数量来缩小组态空间,选取贡献较大的组态.

2.2 重粒子碰撞动力学计算

非辐射分子轨道密耦合方法(QMOCC)对于重离子散射系统,采用质心坐标和原子单位,两原子体系碰撞系统的总哈密顿量表示为

式中,R为入射离子相对靶粒子核间距,V为所有电子以及原子核的库仑相互作用之和,质量项M=M1+M2,µ=M1M2/M,m=M/(M+1),注意(2)式忽略了极化相互作用项.

令ϕi为电子总波函数,在R→∞时候,电子相对于原子核运动,以核为中心,电子总波函数能在绝热表象下有如下形式:

式中,e xp[iγ(R,r)] 称电子转移因子.在微扰的稳态近似下,可以忽略电子转移因子,把系统的总波函数近似用绝热电子波函数代替,利用Born-Oppenheimer 近似,则总波函数可以用电子绝热波函数展开:

其中对i的求和限于完备的绝热矢量集合{ψi}中的子集.而且,每一个ψi在渐进区对于这不同的原子态,这些原子态也称为通道.

将(4)式代入能量本征方程,可得到微扰的稳态方程:

式中,I为单位矩阵,u为对角的绝热势矩阵,uij=εjδij,εj是绝热态的本征能量,M(R) 和>P(R)是耦合矩阵分别满足:

在球坐标系里,(5)式可以写为

对于求解(12)式,定义一个新的函数gl,满足fl=Cgl,其中C是正交变换矩阵.若f是(12)式的一个解,那么g同样是另一个解,因此可以这样构建C:

式中u是对角的绝热势矩阵,Uγ,γ′是非绝热势矩阵,P是转动耦合矩阵.(14)式满足以下边界条件:

其中jJ和ηJ分别为通道的规则和非规则的库仑函数,Kl为实对称的K矩阵.从K矩阵可以得到S矩阵:

其中Sl表示第l个分波对应的S矩阵.

对于速率系数的计算,采用Maxwellian-Boltzmann 分布对散射截面求平均,那么反应速率为

其中,k为玻尔兹曼常数,T为温度,µ是约化质量.

3 计算结果和讨论

对于BH+分子的电子态,总共计算了9 个2Σ+态和6 个2Π 态,这15 个电子态的绝热势能曲线如图1 所示,横坐标为原子核间距,纵坐标是电子态能量.从图1(a)可看到较低的5 个分子态之间有较大的能量差,较高的激发态能级比较密集,处于近简并的状态.电子态之间的避免交叉近区相护作用很强烈,这些避免交叉现象在耦合矩阵元中也有明显的表现.图1(b)中,在R=3.8 Å 处,32Π 和42Π态有一个显著的避免交叉,而分别在R=2.3,3.2,4.6 Å 处,42Π 和 52Π 也有比较明显的避免交叉现象.对于QMOCC 的计算,这些避免交叉能量相近的点起到关键的作用,因为绝热分子态的耦合构成了非辐射电子转移的主要途径.

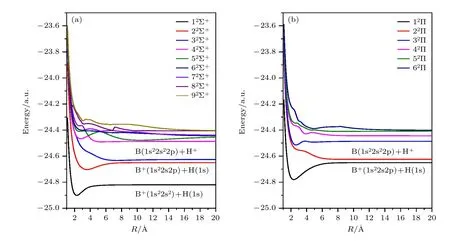
图1 (a) BH+分子 Σ 态势能曲线;(b) BH+分子 Π 态势能曲线Fig.1.(a) Energy curve of BH+ molecule with Σ states;(b) energy curve of BH+ molecule with Π states.

为了保证后续动力学计算的准确性,表1 列出了这15 个电子态的理论结果和实验结果,以及各个不同分子态解离极限所对应的原子态.在QMOCC 的理论框架下,散射末态对应的原子能级与分子态解离极限对应的原子态一一对应.上述计算构建的散射矩阵,可以清晰说明不同散射通道之间跃迁的物理信息.从表1 还可以看到,分子态的解离极限涉及的原子态能级最大到2p 电子轨道,电子从B 原子的转移主要来源于2s 和2p 电子轨道.除了非弹性的散射通道之外,计算还包括一些弹性散射通道,如分子态 32Σ+和 22Π .这些弹性散射通道与非弹性散射通道的耦合,对最终散射态之间的跃迁有不可忽略的影响.

表1 不同分子态对应的解离极限下的原子态以及态能量的理论结果和实验结果Table 1.Atomic states corresponding to different molecular states under dissociation limit,and the theoretical and experimental results of state energy.

表1 中所有的散射通道都被考虑在QMOCC计算内,计算能区从 10-3— 103eV/u .图2 和图3分别为B 原子2s 和2p 轨道的电子转移截面随入射能量变化的函数图像.在图2 中,对分子的态的精细结构也进行区分,分别为3P 和1P 态.因为1P态的散射通道能量较高,所以需要较大的入射能量,该通道才被打开.在图3 中,将两个2p 轨道的电子转移截面加和,得到2p 轨道的电子转移总截面.然而,从图3 可以得到,2s 和2p 轨道的电子转移截面在计算的能区范围内,有至少两个数量级的差异.所以内壳层的2s 轨道的电子转移在整个电子转移过程中占主导地位.因为QMOCC 考虑各种电子态的散射通道之间的耦合,从图3 可以看到,在低于1 eV/u 能量,电子转移截面具有较多的 共振 现象.尤其在靠近 10-3eV/u 能 量附 近,2s 和2p 轨道的电子转移截面都有强烈的共振,这是低能区碰撞过程量子效应比较强的一种表现.重粒子碰撞过程中,往往内壳层的电子转移都会伴随退激发光辐射现象.

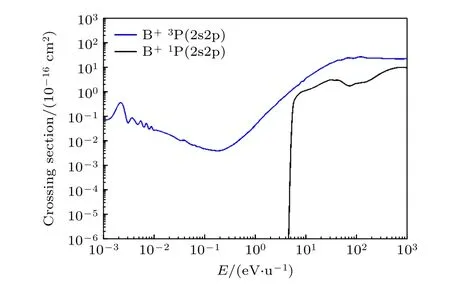
图2 质子碰撞B 原子过程中2p 轨道电子转移截面Fig.2.Electron transfer cross section of 2p orbitals in the process of protons colliding with B atom.

图3 质子碰撞B 原子过程中2s 和2p 轨道电子转移截面Fig.3.Electron transfer cross section of 2s and 2p orbitals in the process of protons colliding with B atom.

对于质子碰撞B 原子,如表1 所列,电子转移通道包括 12Σ+,22Σ+,12Π+,42Σ+,32Π+,42Π+,52Σ+,62Σ+,82Σ+和 52Π+这10 个绝热分子态,其中涉及内壳层2s 电子转移的通道有6 个,导致外壳层2p 电子转移的通道有4 个.弹性通道有32Σ+,22Π 两个绝热分子态,其开通道能量为5.3 eV左右,所有其在低能区并未与电子转移通道存在竞争关系.此外,还有3 个电子从2p 轨道跃迁到3s轨道的激发通道,分别是 72Σ+,92Σ+和 62Π+绝热分子态,激发通道都需要较大的能量才能打开,主要贡献都在于与其他电子转移通道耦合.图4 和图5为部分耦合较强的绝热分子态之间的径向耦合矩阵元和转动耦合矩阵元随核间距的变化.从图4 可以看到,径向耦合中,分子态 52Σ+-62Σ+之间的耦合最强,这两个通道都对2p 轨道的电子转移有贡献.而且,除了分子态 22Σ+-32Σ+的耦合为2s轨道的电子转移有影响,剩下几个耦合比较强的径向耦合矩阵元,比如 12Σ+-22Σ+和42Σ+-52Σ+也都对2p 轨道的电子转移有影响.然而,2s 轨道的电子转移涉及较多的绝热分子态通道,所以其总体截面大于2p 轨道电子转移.虽然,影响2p 轨道电子转移的径向耦合强度较大,但是图3 的计算说明,这些耦合更多的造成2p 轨道电子转移截面的减小.

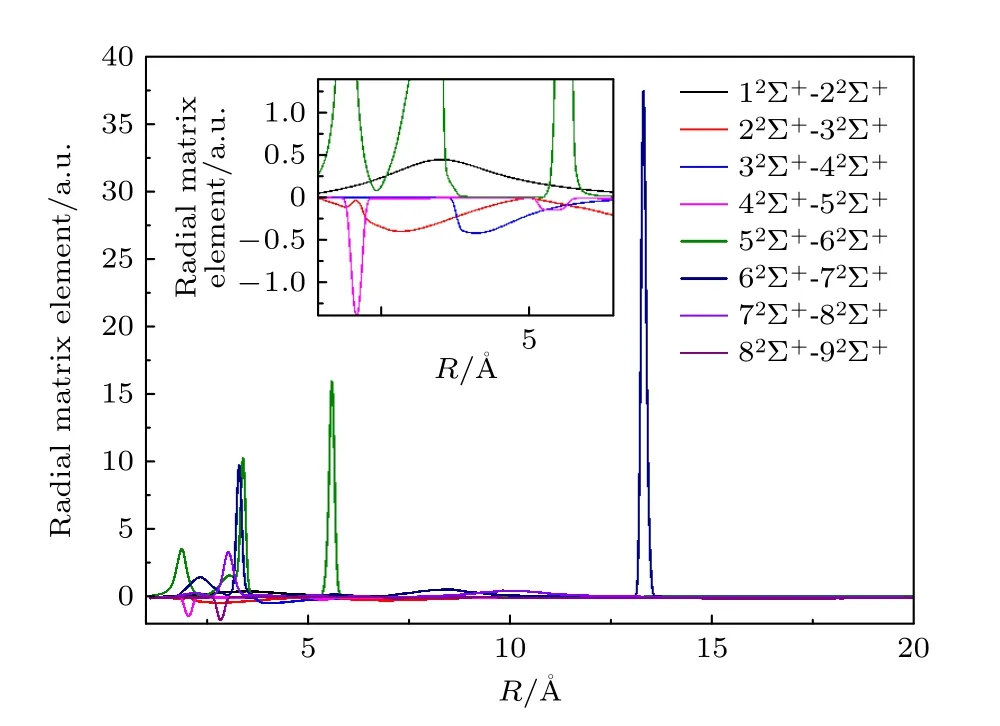
图4 径向耦合矩阵元随核间距的变化Fig.4.Radial coupling matrix element changes with the nuclear distance.

图5 转动耦合矩阵元随核间距的变化Fig.5.Rotation coupling matrix element varies with the nuclear distance.

同样图5 中最大的两个转动耦合矩阵元分别是分子态 42Π—52Π 和 52Π—62Π .其中42Π—52Π之间的转动耦合也是影响2p 轨道电子转移,但52Π—62Π 之间的耦合却对 2s 轨道的电子转移有贡献.42Π,52Π,62Π 三个态是较高的激发态,因为要打开最低能量的态 42Π 也需要一定入射能量,所以转动耦合虽然大,但是对电子转移过程在低能区的影响极其有限.涉及2s 轨道的电子转移通道,虽然耦合贡献不及2p 轨道电子,但是这些通道对应的分子态大多处于较低能级,且数量较多,所以最终计算的2s 轨道的电子转移截面远大于2p 轨道电子.

在表2 中,考虑整个系统服从麦克斯韦-玻尔兹曼能量分布.计算的电子总的转移速率系数α(T),计算的温度点量级从101—107,这个温度跨度范围比较广泛,可以反映宏观系统电子转移的物理性质,注意计算的电子转移的速率将包含2s 和2p 轨道.从表2 还可以发现,因为相对高能态,低能态的布局对速率系数的影响较大,随着温度的升高,电子转移总速率系数增长幅度越来越平缓.当温度高于105K,系统的电子转移总速率变化幅度明显小于低温区.虽然我们考虑总的电子转移速率,但是2s 轨道电子转移占绝对主导地位,所以总的电子转移速率,也可以在一定程度上反映内壳层电子转移后导致的X 射线辐射的强度.

表2 电子转移总的速率系数,其中包含2s 和2p 轨道的电子转移Table 2.Total rate coefficient of electron transfer,including electron transfer of 2s and 2p orbitals.

4 结论

采用QMCOCC 全量子的理论方法,研究了质子碰撞B 原子电荷转移过程.通过MRDCI 的第一性原理计算,得到了耦合分子9 个2Σ+态和6 个2Π 态,取得了与实验测量较好的结果.得到的分子态势能曲线可避免交叉,这些能量点的避免交叉对绝热分子态耦合具有重要的意义.本文所计算的15 个散射通道中,不仅包含弹性散射通道,还有电子激发和转移的非弹性散射通道.其中,电子转移通道都集中在中低能区,而电子激发处于较高能区.经过计算,得到了从 10-3— 103eV/u 的质子入射能区的电子转移截面,并发现在低能区出现较强的共振现象,这主要是因为低能区通道耦合造成的散射量子效应.电子转移截面分为2s 和2p 轨道的电子转移截面,其中2s 轨道的电子转移截面占据绝对主导地位.这些内壳层的电子转移过程,往往伴随这高能量的辐射退激发发光想象.从15 个通道分析,发现包含2s 轨道的电子转移的绝热分子态数量最多,且这些通道的所需要的开通道能量也比较小.此外,还计算了大能量跨度的电子转移速率系数,为等离子体模拟提供重要的原子参数.对于宏观大尺度系统的电子转移过程,低能区的散射截面占比较大.通过计算也验证了这点,研究发现电子转移速率随着系统温度的升高,增长的幅度越来越小.众所周知,B 元素在天体中的丰度也较高,所以第一性原理计算不仅可以提供精确的原子参数,也可以帮助人们深入认识质子碰撞B 原子的物理机制.

感谢西安建筑科技大学理学院和北京应用物理与计算数学研究所对本工作的支持.