AlH 分子10 个Λ-S 态和26 个Ω 态光谱性质的理论研究*

邢伟 李胜周 孙金锋 曹旭 朱遵略 李文涛 李悦毅 白春旭

1) (信阳师范大学物理电子工程学院,信阳 464000)

2) (河南师范大学物理学院,新乡 453000)

3) (潍坊科技学院,寿光 262700)

在修正了各种误差(自旋-轨道耦合效应、标量相对论效应、核价相关效应及基组截断)的基础上,本文利用内收缩的多参考组态相互作用(icMRCI) +Q 方法计算了AlH 分子10 个Λ-S 态和26 个Ω 态的势能曲线.利用包含自旋-轨道耦合效应的icMRCI/AV6Z*理论计算了态之间的跃迁偶极矩.计算得到的光谱常数和跃迁数据与现有的实验值符合很好.研究发现:1) (0,2),(1,0),(1,1),(1,2),(1,3),(1,4)和(1,5)带Q(J'')支的跃迁比较强,随着J''的增大,Δυ=0 带的爱因斯坦A 系数和振动分支比值逐渐减小,加权的吸收振子强度值逐渐增大;Δυ ≠ 0 带的爱因斯坦A 系数、振动分支比和加权的吸收振子强度值逐渐增大;2) A1Π1 态υ'=0 和1 能级的辐射寿命随着J'的增大而缓慢增大;3) AlH 分子的跃迁满足双原子分子激光冷却的准则,即对角化分布的振动分支比,A1Π1(υ'=0 和1,J'=1,+)态极短的辐射寿命, a 3Π0+,a3Π1 和a3 Π2 中间电子态不会对激光冷却产生干扰.因此,基于1,—)循环跃迁,本文提出了激光冷却AlH 分子的可行性方案,冷却时使用四束可见光波段的泵浦激光就可以散射2.541×104 个光子,这足以冷却到超冷温度,并且主跃迁的多普勒温度和回弹温度为µK量级.

1 引言

AlH 分子在天体物理[1-5]和激光直接冷却极性分子[6]等方面扮演重要的角色.例如,Herbig[1]在米拉变星天鹅座χ,Kamiński 等[2]在米拉变星鲸鱼座o的光球,Pavlenko 等[3]在半人马座比邻星,Karthikeyan 等[4]在太阳黑子的发射光谱发现了AlH 分子,Halfen 和Ziurys[5]预测在晚型恒星的星周包层中可能存在AlH 分子.此外,AlH 分子是潜在的激光冷却和俘获材料[6].AlH 分子精确的光谱和跃迁数据在恒星大气和星际空间中AlH 分子的识别、恒星大气模型的构建以及AlH 分子激光冷却方案的构建等方面起着至关重要的作用.

实验上自1901 年Basquin[7]首次对AlH 分子光谱观测以来,科学家们通过电子吸收、发射和振动-转动光谱研究了AlH 分子的X1Σ+,a3Π,A1Π,b3Σ—,C1Σ+态的光谱性质,并在红外线、可见光和紫外线中识别出许多带[4,5,7-21].例如,Halfen 和Ziurys[5]利用太赫兹直接吸收光谱测量了755 GHz 附近AlH 分子X1Σ+态J=2 ← 1 的转动光谱.Deutsch等[8]利用发射光谱测量了AlH 分子X1Σ+(Δυ=2,υ=0—8)带.White 等[9]和Ito 等[10]利用高分辨率红外发射技术研究了X1Σ+态的振动-转动光谱.Karthikeyan 等[4]利用观测到的太阳黑子的高分辨率傅里叶变换光谱,对AlH 分子A1Π → X1Σ+(0,0)和(1,1)带转动线的存在进行了研究.Rice等[11]利用发射光谱技术测量了A1Π → X1Σ+(0,0),(0,1),(1,0),(1,1)和(1,2)带的爱因斯坦A系数的比率、振子强度的比率和振动跃迁概率的比率.Ram 和Bernath[12]利用傅里叶变换发射光谱测量了A1Π → X1Σ+(0,0)和(1,1)带.Baltayan和Nedelec[13]利用染料激光激发光谱测量了A1Π(υ'=0,1)的辐射寿命.Szajna 研究组[14-16]利用高分辨率的常规光谱技术研究了可见光区域A1Π →X1Σ+(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(1,3)带和C1Σ+→ A1Π (0,0)和(1,1)带,紫外区域C1Σ+→ X1Σ+(0,0),(1,1)和(1,2)带.最近,Szajna 研究组[17]采用傅里叶变换光谱仪观测到AlH 的高分辨率可见光发射光谱,覆盖了A1Π → X1Σ+系统的(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(1,3)和(1,4)带.Zhang 和Stuke[18]利用可调谐染料激光质谱法研究了C1Σ+→ X1Σ+跃迁(0,0),(1,0)和(1,1)带.Zhu 等[19]利用激光诱导荧光法测量和分析了AlH 分子C1Σ+← X1Σ+(0,0)带和b3Σ—← X1Σ+(0,0)和(1,0)带.Tao 等[20]报道了25500—26400 cm—1紫外区域内AlH 分子b3Σ—→ a3Π (0,0)带的激光荧光激发光谱.在25900—26500 cm—1紫外区域内,Szajna 等[21]利用高精度色散光谱技术测量了AlH 分子b3Σ-→ a3Π (0,0)和(1,1)带.这些实验研究[4,5,7-21]旨在确定所涉及辐射跃迁的线波数,A1Π (υ'=0,1)和b3Σ—(υ'=0)的寿命,基态(X1Σ+)和激发态(a3Π,A1Π,b3Σ—和C1Σ+)的光谱常数和分子常数.但未报道这些电子态之间跃迁的振动分支比、吸收振子强度和加权的吸收振子强度、波长、激发态的辐射宽度等数据及考虑自旋-轨道耦合效应后Ω 态的光谱数据.近年来,随着ab initio方法的快速发展,理论科学家对AlH 分子的电子结构进行高精度的研究.Wells 和Lane[6],Woon 和Dunning[22]以及Shi 等[23]利用多参考组态相互作用(MRCI)方法和相关一致基组计算了AlH 分子基态(X1Σ+[6,22,23])和激发态(a3Π,A1Π,13Σ+,b3Σ—,23Σ+,23Π,C1Σ+,15Σ—和15Π)[6]的势能曲线,并报道了束缚的单重态和三重态的部分光谱常数、A1Π 和a3Π 态到 X1Σ+态跃迁P(1)支的波数和Franck-Condon 因子[6]、并基于A1Π→X1Σ+跃迁对角化的Franck-Condon 因子研究了激光冷却AlH 分子的可行性[6].Tao 等[20]利用内收缩(ic)的icMRCI/aug-cc-pV5Z(AV5Z)理论计算了X1Σ+,a3Π,13Σ+,b3Σ—,23Σ+和C1Σ+的势能曲线、13Σ+和b3Σ—态之间的自旋-轨道耦合矩阵元,并报道了X1Σ+,a3Π 和b3Σ—态υ=0 能级的部分光谱常数(T0和B0).基于Davidson 修正(+Q),Zhao 等[24]使用MRCI+Q/AV5Z 理论计算了X1Σ+,a3Π,A1Π,13Σ+和C1Σ+态的势能曲线以及A1Π 态到X1Σ+态的跃迁偶极距,报道了束缚态的光谱常数和A1Π 态的寿命.Qin 等[25]利用icMRCI+Q/aug-cc-pV6Z(AV6Z)理论计算了8个单重态(X1Σ+,A1Π,C1Σ+,31Σ+,21Π,31Π,41Σ+,41Π)的势能曲线和7 个激发态到X1Σ+态的跃迁偶极距,报道了这些态的光谱常数、从基态到7 个激发态跃迁的光解离截面和光解离率.Gutsev 等[26],Brown 和Wasylishen[27],Hirata 等[28]以及Karton和Martin[29]分别利用不同级别的耦合簇理论[CCSD(T)[26,27],DK3-CCSD[28],DK3-CCSDT[28],DK3-CCSDTQ[28],W4-CCSDTQ[29]]计算了X1Σ+[26-29]和a3Π[26]态的电子结构,并报道了这两个态的光谱常数.Ferrante 等[30]利用冻结核完全组态相互作用(FCI)方法获得了X1Σ+态完全基组极限时的势能曲线,并报道了X1Σ+态的光谱常数.Koput[31]纳入相对论效应、绝热和非绝热效应并利用多参考平均耦合对泛函(MR-ACPF)方法和aug-cc-pCVnZ(n=5—7)基组计算了X1Σ+态的势能曲线,并报道了部分光谱常数.Yurchenko 等[32]基于拟合实验数据得到的势能曲线及从头算跃迁偶极距曲线,通过求解核运动薛定谔方程,获得了AlH 分子X1Σ+和A1Π 态的振动-转动解析列表(态的寿命、爱因斯坦A系数、跃迁波数和1—5000 K 内的配分函数等数据).Sindhan 等[33]利用Rydberg-Klein-Rees(RKR)势对实验振动能级进行数值积分计算了AlH 分子A1Π → X1Σ+和C1Σ+→ A1Π 辐射跃迁参数.

综上所述,实验和理论科学家们已对AlH 分子的基态和低电子激发态的电子结构和跃迁特性进行了一系列的研究.然而,考虑自旋-轨道耦合效应后激发Ω 态的光谱和跃迁数据仍然未知.虽然Wells 和Lane[6]基于A1Π→X1Σ+跃迁的Franck-Condon 因子(计算值)和跃迁频率(实验值)构建了AlH 分子的激光冷却方案,但是他们未计算A1Π→X1Σ+的跃迁偶极矩,相应的未报道爱因斯坦A系数和A1Π 态的辐射寿命等数据,另外他们未研究中间态 a3Π0+,a3Π1和a3Π2对激光冷却的影响,也就无法确定AlH 分子是否满足双原子激光冷却的第二和第三准则(A1Π1态短的辐射寿命,a3Π0+,a3Π1和a3Π2中间电子态不会对激光冷却产生干扰)[34].因此,本文纳入标量相对论效应、自旋-轨道耦合效应、核价相关效应和外推势能到完全基组极限对AlH 分子10 个Λ-S 态和26 个Ω 态的电子结构、光谱和跃迁特性进行系统深入的研究,并利用振动分支比、加权的吸收振子强度、激发态的辐射寿命和辐射宽度分析激光冷却AlH 分子的可行性,进而构建激光冷却AlH 分子的振动-转动方案,并评价冷却效果.

2 计算方法

H 原子2p2Pu← 1s2Sg的激发能大于Al 原子3s24s2Sg← 3s23p2Pu和3s3p24Pg← 3s23p2Pu的激发能[35].因此,AlH 分子的第一离解极限为Al(3s23p2Pu)+H(1s2Sg),并且此离解极限生成AlH(X1Σ+,a3Π,A1Π,13Σ+);第二离解极限为Al(3s24s2Sg)+H(1s2Sg),这个离解极限生成AlH(C1Σ+,23Σ+);第三离解极限为Al(3s3p24Pg)+H(1s2Sg),此离解极限生成AlH(b3Σ—,23Π,15Σ—,15Π).自旋-轨道耦合效应使这10 个Λ-S 态分裂为26 个Ω 态.本文在MOLPRO 2010.1 程序包[36]C2v点群中对AlH 分子的电子结构进行从头计算.首先基于Hartree-Fock 方法得到X1Σ+态的初始猜测分子轨道和电子波函,接着使用态平均的完全活性空间自洽场(SA-CASSCF)方法对初始猜测分子轨道和波函进行优化,获得并分析X1Σ+态和 9 个激发 ΛS 态不同键长处自然轨道能量,得到各电子态在各自平衡位置附近的电子组态,最后采用icMRCI +Q方法计算10 个Λ-S 态的势能.因为基组和活性空间的选择决定了SA-CASSCF 和icMRCI +Q计算的精度[37,38],为了获得高精度的结果,对H 原子选用AV5Z 和AV6Z 基组[39],对Al 原子选用aug-cc-pV(5+d)Z[AV(5+d)Z]和aug-cc-pV(6+d)Z[AV(6+d)Z][40]基组.将以上的混合基组分别记为AV5Z*和AV6Z*.活性空间由5 个价轨道(Al 原子的3s3p 轨道和H 原子的1s 轨道)和1 个虚轨道(Al 原子4s 轨道)组成,记为(4e,6o).在0.10400—1.0840 nm 的核间距内,步长为0.02 nm;在0.14400—0.24200 nm 的核间距内,即每个态的平衡位置附近,步长为0.002 nm.

为了获得这10 个Λ-S 态完全基组极限时精确的势能曲线,基于上述计算,本文修正了标量相对论效应、核价相关效应和基组截断带来的误差.具体修正方法为: 基于icMRCI+Q/aug-cc-pV5ZDK(AV5Z-DK)[41]理论,利用三阶Douglas-Kroll-Hess (DKH3)[42]近似计算标量相对论效应贡献的势能(表示为+SR);利用icMRCI +Q/aug-ccpCV5Z(ACV5Z)[43]理论计算核价相关效应贡献的势能(表示为+CV),其中,全电子计算时,AlH分子活性空间中的4 个电子和Al 原子2s2p 闭壳层轨道的8 个电子参与计算;冻结核计算时,AlH 分子活性空间中的4 个电子参与计算;本文使用Oyeyemi 等[44]的外推方案,通过将icMRCI +Q/AV5Z*和icMRCI+Q/AV6Z*获得的参考能和相关能分别外推得到10 个Λ-S 态完全基组极限的势能,表示为icMRCI+Q/56;将标量相对论效应和核价相关效应贡献的势能加到icMRCI+Q/56 势能里,便得到icMRCI+Q/56+CV+SR理论水平上10 个Λ-S 态的势能曲线,如图1 所示.

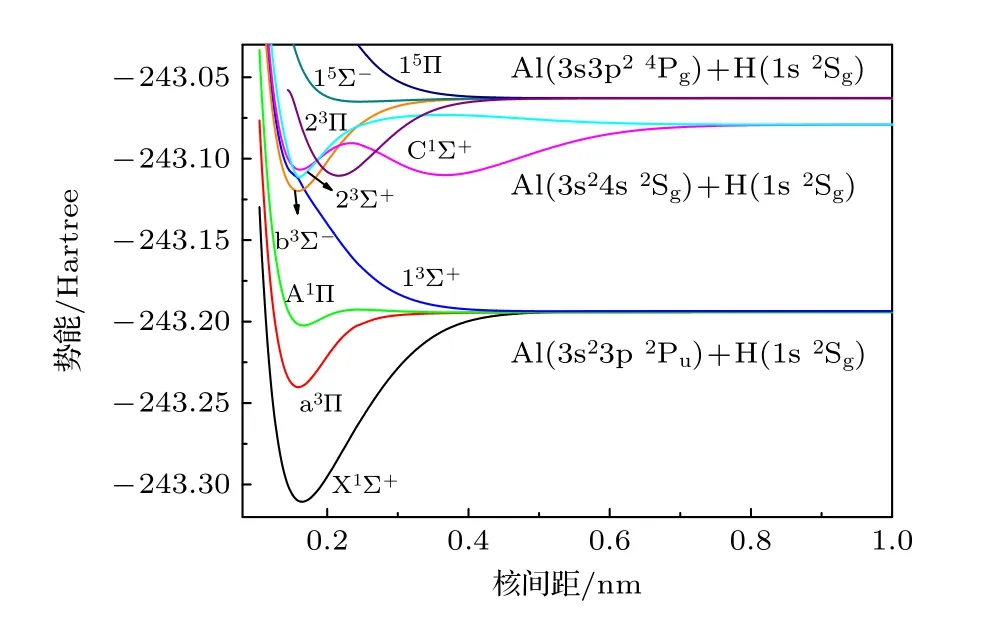
图1 AlH 分子10 个Λ-S 态的势能曲线Fig.1.Potential energy curves of 10 Λ-S states of the AlH molecule.

(1)式—(7)式中,g为低能量态振转能级的统计权重;Ai,υ'J'是从高能量态能级υ'J'发射的第i个系统的总爱因斯坦A系数.

3 结果与讨论

3.1 8 个Λ-S 态的光谱常数

icMRCI+Q/56+CV+SR 理论水平上计算的10 个Λ-S 态的离解关系列于表1.由表1 可知,本文结果与实验值[35]符合非常好,例如第二离解极限和第三离解极限的相对能量分别比实验值[35]小74.43 cm—1(0.2943%)和229.89 cm—1(0.7922%),仅Qin 等[25]报道的第二离解极限的相对能量比本文的计算值稍微接近实验值[35].

表1 AlH 分子前3 个离解极限产生的10 个Λ-S 态的离解关系Table 1.Dissociation relationships of the 10 Λ-S states generated from the first three dissociation asymptotes of the AlH molecule.

仅以X1Σ+态为例,简要讨论基组截断误差、核价相关和标量相对论修正分别在总能量中的比重和对计算结果的精度的影响.在0.10400 —1.0840 nm 的核间距内,基组截断误差修正使icMRCI+Q/AV6Z*理论计算的X1Σ+态的能量降低0.000307—0.000572 Hartree,在总能量中的比重为1.261×10—4%—2.353×10—4%.核价相关效应贡献的势能为—0.321265 到—0.315680 Hartree,在总能量中的比重为0.1298%—0.1321%.标量相对论效应贡献的势能为—0.437010 到—0.436652 Hartree,在总能量中的比重为0.1795%—0.1797%.为了阐明基组截断误差、核价相关效应和标量相对论效应对光谱常数的影响,表2 为icMRCI+Q/AV6Z*,icMRCI+Q/56,icMRCI+Q/56+CV,icMRCI+Q/56+SR 和icMRCI+Q/56+CV +SR 理论获得的光谱常数、挑选的实验值[8-10,13-15,18]和其他理论值[6,22-31].由表2 可知,基组截断误差修正使Re减少了4×10—5nm,使ωe,Be和De分别增大0.93 cm—1,0.00301 cm—1和0.0047 eV,它们与实验值[8-10,13-15,18]的最大偏差分别减少4×10—5nm (精度提高0.0243%),0.93 cm—1(精度提高0.0553%),0.00301 cm—1(精度提高0.0471%)和0.0047 eV (精度降低0.1487%).为了进一步提高光谱常数的计算精度,在icMRCI+Q/56 理论基础上考虑核价相关效应和标量相对论效应.

表2 AlH 分子X1Σ+态的光谱常数Table 2.Spectroscopic parameters of the X1Σ+ state of AlH molecule.

由表2 可知,仅考虑核价相关修正时,Re和De分别减小了8.9×10—4nm 和0.054 eV,ωe和Be分别增大了17.95 cm—1和0.04377 cm—1;仅考虑标量相对论修正时,Re增大了2×10—5nm,ωe,Be和De分别减小了2.76 cm—1,0.00118 cm—1和0.0035 eV;可见,核价相关修正对光谱常数的影响比标量相对论修正对光谱常数的影响显著.同时考虑这两种修正时,Re和De分别减小了8.7×10—4nm和0.0575 eV,ωe和Be分别增大了15.26 cm—1和0.04313 cm—1,它们与实验 值[8-10,13-15,18]的最大偏差分别减小5×10—5nm(精度提高0.0308%),12.47 cm—1(精度提高0.7411%),0.04313 cm—1(精度提高0.6746%)和0.0575 eV(精度提高1.8196%).由此可得,当进行高精度计算时,还必须考虑这两种修正.综上分析,我们将利用icMRCI+Q/56 +CV+SR 理论获得的光谱常数进行讨论.

X1Σ+态在Re处的主要价电子组态为4σ25σ22π06σ07σ0(89.52%).其势阱深度为25669.75 cm—1,包含26 个振动态.由表2 可知,本文计算的Re,ωe,Be和De与实验值[8-10,13-15,18]吻合很好,它们与实验值[8-10,13-15,18]的最大偏离分别为0.00051 nm(0.3096%),1.49 cm—1(0.0886%),0.04195 cm—1(0.6561%)和0.0225 eV (0.7120%);仅文献[25,27—31]中的Re值、文献[23,29,30]中的ωe值、文献[23,25,27,28,30]中的Be值和文献[22,23,28,31]中的De值与实验值[8-10,13-15,18]的最大偏离稍微小于本文的结果.

由图1 可知,除了排斥态13Σ+和15Π 之外,其他8 个Λ-S 态为束缚态.为便于讨论,表3 列出了计算的7 个束缚Λ-S 激发态的光谱常数、挑选的实验值[13-17,19,20]和其他理论值[6,20,24-26].

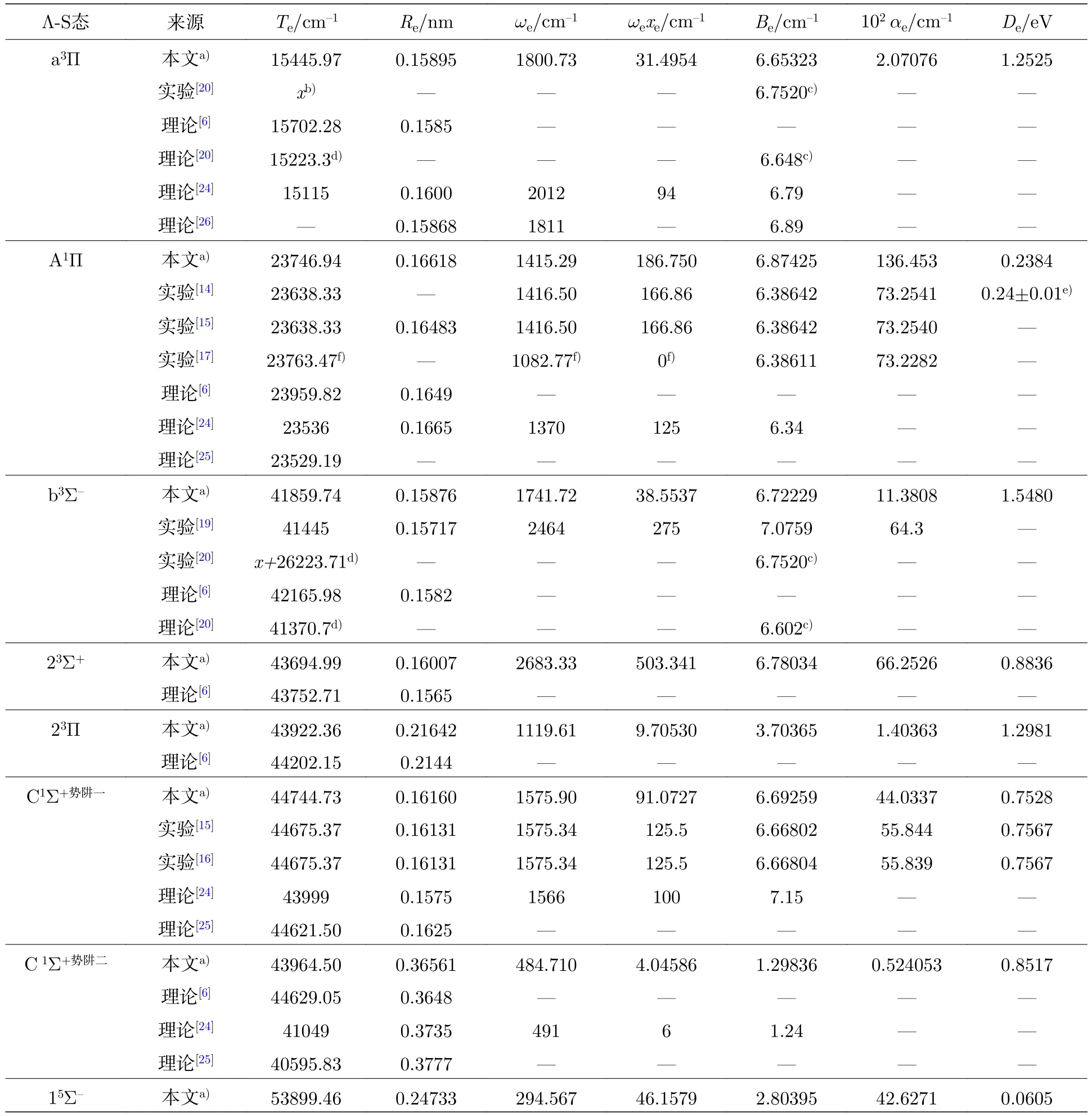
表3 AlH 分子a3Π,A1Π,b3Σ—,23Σ+,23Π,C1Σ+和15Σ—态的光谱常数Table 3.Spectroscopic parameters of the a3Π,A1Π,b3Σ—,23Σ+,23Π,C1Σ+,and 15Σ— states of AlH.

5σ1→ 2π1的电子激发形成a3Π 和A1Π 态,它们在各自Re处的主要价电子组态分别为4σ25σ12π16σ07σ0(89.72%)和4σ25σ12π16σ07σ0(88.39%).a3Π态的势阱深度为10102.42 cm—1,包含10 个振动态.本文计算的a3Π 态的惯性转动常数Bυ(υ=0,1)分别为6.74781 cm—1和6.49597 cm—1,它们分别比Szajna 等[21]报道的相应值稍大0.03872 cm—1(0.5771%)和0.04273 cm—1(0.6621%).A1Π 态 在R=0.244 nm 附近出现势垒,势垒顶部的势能高于无穷远处的势能,势阱深度为2145.17 cm—1,包含2 个振动态,这与实验[11-15,17]和理论[6,24,25]的结论相同.由表3 可知,本文计算的A1Π 态的Te,Re,ωe和De与实验值[13-15,17]吻合得也很好,它们与实验值[13-15,17]的最大偏差分别为108.61 cm—1(0.4595%),0.00135 nm (0.8190%),1.21 cm—1(0.0854%)和0.0016 eV (0.6667%).

5σ → 2π 的双电子激发形成b3Σ—态,其在Re处的主要价电子组态为4σ25σ02π26σ07σ0(84.37%).b3Σ—态的势阱深度为12485.91 cm—1,包含12 个振动态.5σ → 6σ 的单电子激发形成排斥态13Σ+,它与b3Σ—态在R=0.16716 nm 处交叉,计算表明b3Σ—态的预解离始于υ'=0 能级.排斥态13Σ+通过5σ → 6σ 的单电子激发形成.

5σ→7σ 的单电子激发形成23Σ+态和C1Σ+势阱一态,它们在各自Re处的主要价电子组态分别为4σ25σ12π06σ07σ1(91.10%)和4σ25σ12π06σ07σ1(89.15%).由图1 可知,在R=0.15800 nm 附近,23Σ+态与13Σ+态避免交叉,以致23Σ+态形成势阱.23Σ+态势阱深度为7122.83 cm—1,包含5 个振动态.C1Σ+态在R=0.23400 nm 附近出现势垒,势垒低于无穷远处,第1 个势阱深度为3561.94 cm—1,包含3 个振动态.由表3 可知,本文计算的C1Σ+势阱一的Te,Re,ωe和De与实验值[15,16]符合得也很好,其中Te,Re和ωe仅比实验值[15,16]大69.36 cm—1(0.1553%),0.00029 nm (0.1798%)和0.56 cm—1(0.0355%),De与仅比实验值[15,16]小0.0039 eV (0.5154%).C1Σ+态的第2 个势阱具有明显的多参考特征,其在Re处的主要价电子组态为4σ25σ22π06σ07σ0(46.03%),4σ25σ12π06σ17σ0(22.47%)和4σ25σ12π06σ07σ1(11.50%);它的势阱深度为4342.09 cm—1,包含11 个振动态.

4σ1→ 2π1以及5σ2→ 2π16σ1的电子激发形成23Π 态,其在Re处的主要价电子组态为4σ15σ22π16σ07σ0(70.06%)和4σ25σ02π16σ17σ0(12.34%).由图1 可知,在0.18529—0.33399 nm 的核间距范围内,23Π 态与C1Σ+,23Σ+和b3Σ—态交叉,计算表明23Π (υ'≥ 0)能级将受到C1Σ+势阱一(υ'≥ 0),b3Σ—(υ'≥ 1),23Σ+(υ'≥ 1)和C1Σ+势阱二(υ'≥ 7)能级的微扰.

4σ15σ1→ 2π2的电子激发形成15Σ—弱束缚态,其在Re处的主要价电子组态为4σ15σ12π26σ07σ0(96.67%).它的势阱深度为488.33 cm—1,仅包含3 个振动态.排斥态15Π 通过4σ1→ 2π1和5σ1→6σ1的电子激发形成.

3.2 19 个Ω 态的光谱常数

自旋-轨道耦合效应使AlH 分子前3 个离解极限Al(3s23p2Pu)+H(1s2Sg),Al(3s24s2Sg)+H(1s2Sg)和Al(3s3p24Pg)+H(1s2Sg)分裂成6 条离解极 限,即Al(3s23p2P1/2)+H(1s2S1/2),Al(3s23p2P3/2)+H(1s2S1/2),Al(3s24s2S1/2)+H(1s2S1/2),Al(3s3p24P1/2)+H(1s2S1/2),Al(3s3p24P3/2)+H(1s2S1/2)和Al(3s3p24P5/2)+H(1s2S1/2).表4 中列入了这6 个离解极限的能量间隔及它们所产生的26 个Ω 态.

表4 AlH 分子26 个Ω 态的离解关系Table 4.Dissociation relationships of the 26 Ω states of the AlH molecule.

由表4 知,本文计算的Al 原子的自旋-轨道耦合分裂值与实验值[35]符合得很好,它们分别比相应的实验值[35]小8.13 cm—1(3s23p2P3/2— 3s23p2P1/2),66.18 cm—1(3s24s2S1/2— 3s23p2P1/2),259.55 cm—1(3s3p24P1/2— 3s23p2P1/2),254.30 cm—1(3s3p24P3/2—3s23p2P1/2)和249.62 cm—1(3s3p24P5/2— 3s23p2P1/2).本文计算得到的19 个束缚和准束缚Ω 态的光谱常数和Re处Ω 态的构成见表5.

表5 利用icMRCI+Q/56+CV+SR+SOC 理论获得的19 个Ω 态的光谱常数Table 5.Spectroscopic parameters obtained by the icMRCI+Q/56+CV+SR+SOC calculations for the 19 Ω states.

表6 A1Π1 — X 1系统(0,0)和(0,1)带Q 支的振转跃迁Table 6.Rovibrational transitions of the Q branch for the (0,0) and (0,1) bands of the A1Π1 — X 1 system.

表6 A1Π1 — X 1系统(0,0)和(0,1)带Q 支的振转跃迁Table 6.Rovibrational transitions of the Q branch for the (0,0) and (0,1) bands of the A1Π1 — X 1 system.

表7 A1Π1 —X 1 系统(0,2)和(0,3)带Q 支的振转跃迁Table 7.Rovibrational transitions of the Q branch for the (0,2) and (0,3) bands of the A1Π1 — X 1 system.

表7 A1Π1 —X 1 系统(0,2)和(0,3)带Q 支的振转跃迁Table 7.Rovibrational transitions of the Q branch for the (0,2) and (0,3) bands of the A1Π1 — X 1 system.

表8 A1Π1 —X 1 系统(1,0)和(1,1)带Q 支的振转跃迁Table 8.Rovibrational transitions of the Q branch for the (1,0) and (1,1) bands of the A1Π1 —X1 system.

表8 A1Π1 —X 1 系统(1,0)和(1,1)带Q 支的振转跃迁Table 8.Rovibrational transitions of the Q branch for the (1,0) and (1,1) bands of the A1Π1 —X1 system.

表9 A1Π1 — X 1系统(1,2)和(1,3)带Q 支的振转跃迁Table 9.Rovibrational transitions of the Q branch for the (1,2) and (1,3) bands of the A1Π1 — X1 system.

表9 A1Π1 — X 1系统(1,2)和(1,3)带Q 支的振转跃迁Table 9.Rovibrational transitions of the Q branch for the (1,2) and (1,3) bands of the A1Π1 — X1 system.

表10 A1Π1 — X 1系统(1,4)和(1,5)带Q 支的振转跃迁Table 10.Rovibrational transitions of the Q branch for the (1,4) and (1,5) bands of the A1Π1 — X 1 system.

表10 A1Π1 — X 1系统(1,4)和(1,5)带Q 支的振转跃迁Table 10.Rovibrational transitions of the Q branch for the (1,4) and (1,5) bands of the A1Π1 — X 1 system.

表11 a3Π0+ (υ'=0—3,J'=0,+) — X 1(υ''=0—4,J''=1,—)系统的振转跃迁Table 11.Rovibrational transitions of the a 3Π0+(υ'=0—3,J'=0,+) — X 1 (υ''=0—4,J''=1,—) system.

表11 a3Π0+ (υ'=0—3,J'=0,+) — X 1(υ''=0—4,J''=1,—)系统的振转跃迁Table 11.Rovibrational transitions of the a 3Π0+(υ'=0—3,J'=0,+) — X 1 (υ''=0—4,J''=1,—) system.

表12 a3Π1(υ'=0—3,J'=1,+) — X 1(υ''=0 —4,J''=1,—)系统的振转跃迁Table 12.Rovibrational transitions of the a3Π1(υ'=0—3,J'=1,+) — X 1 (υ''=0—4,J''=1,—) system.

表12 a3Π1(υ'=0—3,J'=1,+) — X 1(υ''=0 —4,J''=1,—)系统的振转跃迁Table 12.Rovibrational transitions of the a3Π1(υ'=0—3,J'=1,+) — X 1 (υ''=0—4,J''=1,—) system.

由图1 可知,类似于BH 分子[38],AlH 分子4 个束缚态(X1Σ+,a3Π,A1Π 和15Σ—)和15Π 排斥态的势能曲线也不与其他Λ-S 态的势能曲线发生交叉,在自旋-轨道耦合效应的作用下,X1Σ+,a3Π,A1Π 和15Σ—态分裂为束缚态,15Π 态分裂为 15Π-1, 15Π0-, 15Π0+, 15Π1, 15Π2和 15Π3排斥态.由图1 和图2 可知,这15 个Ω 态势能曲线的形状与相应的5 个Λ-S 态势能曲线的形状相同.由表5 可知,在各自Re处,9 个束缚Ω 态波函的Λ-S 成分几乎全部来自相应的Λ-S 态;由表2,表3和表5 可知,这9 个Ω 态的光谱常数与相应ΛS 态的光谱常数差别很小.在R＜ 0.41208 nm 区域,a3ΠΩ(Ω=0—,0+,1,2)是正常态.Szajna 等[21]报道了a3Π 态的Aυ(υ=0,1)值分别为40.6040和40.4190 cm—1,由公式Aυ=Ae—αAe(υ+1/2),获得Ae=40.6965 cm—1.由表5 可知,在各自Re处,计算的Ae(a3Π1— a3Π0+)=40.04 cm—1和Ae(a3Π2—a3Π1)=40.82 cm—1,它们与实验值[21]符合得很好.a3Π1态势能曲线与 a3Π0+态势能曲线相交于R=0.41208 nm,当R＞ 0.41208 nm 时,a3Π1态的势能小于 a3Π0+态的势能,因此a3Π1态解离为Al(3s23p2P1/2)+H(1s2S1/2), a3Π0+态解离为Al(3s23p2P3/2)+H(1s2S1/2).

图2 AlH 分子26 个Ω 态的势能曲线Fig.2.Potential energy curves of 26 Ω states of the AlH molecule.

图3 AlH 分子 6 对跃迁的跃迁偶极矩曲线Fig.3.Curves of the transition dipole moments versus internuclear separation of six-pair states of the AlH molecule.

图4 利用A1Π1(υ'=0 和1,J'=1,+) ↔ X 1(υ''=0—3,J''=1,—)跃迁进行激光冷却AlH 分子的方案.红色实线表示激光驱动A1Π1(υ'=0 和1,+)← X 1(υ''=0—3,—)跃迁Q(1)支的激光波长(λυ'←υ'')Fig.4.The proposed laser cooling scheme for the AlH using A1Π1 (υ'=0 and 1,J'=1,+) ↔ X 1(υ''=0—3,J''=1,—) transition.The red solid line indicate the wavelength (λυ'←υ'') at which the laser drives the Q(1) branch of the A1Π1 (υ'=0 and 1,+) ←X1(υ''=0—3,—) transition.

在—243.118620 到—243.073393 Hartree 的能量范围内,b3Σ—态势能曲线与13Σ+,23Π,C1Σ+和23Σ+态势能曲线交叉,23Π 态势能曲线还与C1Σ+和23Σ+势能曲线交叉;自旋-轨道耦合效应使这5 个Λ-S态分裂出的9 个Ω=0—,0+和1 组分[(3)0+,(3)1,(4)0+,(3)0—,(4)0—,(4)0+,(5)1,(5)0+和(6)1]出现避免交叉现象,以致这9 个Ω 态势能曲线的形状发生很大变化(图1 和图2).由表3 和表5 可知,这9 个Ω 态的光谱常数也有很大的变化.

23Π2态的势能曲线与其他Ω 态的势能曲线没有避免交叉现象.由图1 和图2 可知,23Π2和23Π态势能曲线的形状相同.由表3 和表5 可知,23Π2和23Π 态的Te,Re,ωe和De差别仅为41.92 cm—1,2×10—5nm,0.01 cm—1和0.0089 eV.

3.3 跃迁特性和激光冷却方案

这些跃迁总Aυ'J'分别为γΣ=1.6278×107s—1,γ1=1.0838 s—1,γ2=0.18752 s—1和γ3=3.9806×10—2s—1,因此

这3 个值都远小于YO 的实验值4.0×10—4[47],这3 对跃迁极小的振动分支损失比表明 a3Π0+,a3Π1和a3Π2态不会对激光冷却产生干扰.

研究了A1Π1态υ'=0 和1 的辐射寿命随转动量子数J′的分布,图5 绘出了A1Π1态υ'=0,J'≤17 和υ'=1,J'≤5 的结果.由图5 可知,υ'=0 和1 的辐射寿命随着J'的增大而缓慢延长.Baltayan 和Nedelec[13]报道的A1Π(υ'=0,J'=7)和A1Π(υ'=1,J'=5)辐射寿命的测量值分别为(66 ± 4)和(83 ± 6) ns,Yurchenko 等[32]报道的计算值分别比实验值[13]大7.60 和19.50 ns,本文计算的相应值分别为62.91 和94.85 ns,可见当前的计算值与实验值[13]符合得较好.因此,本文计算的A1Π1(υ'=0 和1,J'=1,+)的辐射寿命τ01=61.43 ns 和τ11=91.36 ns 也应是精确的,另外我们计算的A1Π1(υ'=0 和1,J'=1,+) → X1(υ'',J''=1,—)的辐射宽度分别为8.642×10—5和5.811×10—5cm—1,这些结果表明可以快速高效地激光冷却AlH 分子.

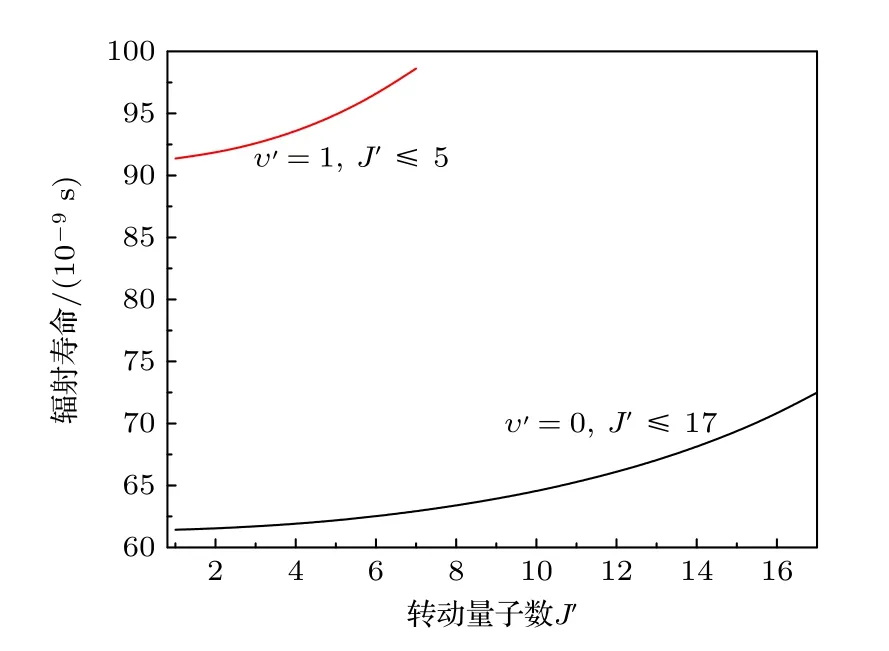
图5 A1Π1 态的辐射寿命随转动量子数J'的分布Fig.5.Distributions of the radiative lifetime varying as the J' of the A1Π1 state.

为了评价激光冷却效果,基于主冷却循环A1Π1(υ'=0,J'=1,+) ↔ X1(υ''=0,J''=1,—)的辐射寿命62.02 ns、激光波长425.30 nm 以及(5)式和(6)式,我们计算了主冷却循环的多普勒温度和回弹温度分别为61.567 µK 和3.782 µK.

4 结论

本文纳入各种相互作用(自旋-轨道耦合效应、标量相对论效应和核价相关效应)并利用icMRCI+Q方法对AlH 分子的电子结构进行从头算,获得了完全基组极限时10 个Λ-S 态和26 个Ω 态精确的势能曲线.在icMRCI/AV6Z*+SOC 理论水平上,获得了态之间6 对跃迁的跃迁偶极矩.并且本文得到的光谱和振转跃迁数据与现有的实验值符合得很好.研究发现以下几点.

2) A1Π1态υ'=0 和1 的辐射寿命随着J'的增大而缓慢延长;

3) A1Π1(υ'=0 和1,J'=1,+) → X1(υ''=0—3,J''=1,—)跃迁满足双原子分子激光冷却的准则: 对角化分布的振动分支比、极短的辐射寿命、 a3Π0+,a3Π1和a3Π2中间电子态不会干扰激光冷却.

因此,基于A1Π1(υ'=0—1,J'=1,+) ↔ X1(υ''=0—3,J''=1,—)跃迁,我们构建了激光冷却AlH 分子的可行性方案.激光冷却AlH 分子时,利用4 束可见光波段的泵浦激光(主泵激光λ0←0=425.30 nm,3 束再泵浦激光λ0←1=457.33 nm、λ1←2=468.68 nm 和λ1←3=505.03 nm)即可散射2.541×104个光子,这足以冷却到超冷温度,并且主冷却循环的多普勒温度和回弹温度分别为61.567 µK 和3.782 µK.这些结果表明AlH 是很好的激光冷却候选分子.