基于ARMA-GARCH组合模型的汇率波动性预测
2023-09-06蔡斌坚

摘 要:文章使用2015年8月11日至2022年11月30日人民币兑美元汇率的日交易中间价数据进行研究。首先对该数据进行对数差分处理,得到平稳的人民币汇率对数收益率序列。其次通过描述性统计分析发现该序列“尖峰厚尾”,而平稳性检验和ARMA模型建立证实了该序列的非随机性质,异方差性检验确认了波动聚集性。研究采用GARCH、EGARCH和TGARCH模型对波动率方程进行拟合,结果显示汇率存在杠杆效应。最终,使用最佳拟合效果的EGARCH(1,2)模型对汇率序列进行回测分析,并提出相关建议。
关键词:ARMA模型;GARCH族模型;杠杆效应
中图分类号:TP391 文献标识码:A 文章编号:2096-4706(2023)14-0129-05
Exchange Rate Volatility Forecasting Based on ARMA-GARCH Combined Model
CAI Binjian
(School of Mathematical Science, South China Normal University, Guangzhou 510631, China)
Abstract: This paper uses daily transaction middle price data of the RMB-USD exchange rate between August 11, 2015 and November 30, 2022 for research. Firstly, the data is processed by logarithmic difference to obtain a stable logarithmic return rate sequence of the RMB exchange rate. Secondly, through descriptive statistical analysis, it is found that the sequence has a “peaked ness and fat tail”. The stationarity test and ARMA model establishment further confirm the non-randomness of the sequence, and the heteroscedasticity test confirms the volatility clustering. This study uses GARCH, EGARCH and TGARCH models to fit the volatility rate equation, and the results show that there is a leverage effect in the exchange rate. Finally, the EGARCH (1, 2) model with the best fitting effect is used for backtesting analysis of the exchange rate sequence, and relevant suggestions are proposed.
Keywords: ARMA model; GARCH family model; leverage effect
0 引 言
2015年8月11日,央行改革了人民幣对美元中间汇率报价机制,增强了人民币汇率与汇率市场的紧密联系,也加强了汇率在经济和金融领域的作用,但同时也增强了人民币汇率的波动性。自2018年3月,中美贸易战爆发以来,人民币汇率市场大幅震荡。2020年1月21日新冠疫情大规模扩散之后,人民币汇率快速上升,对经济造成了一定的冲击。
随着我国经济水平不断提高和全球化不断发展,中国的经济发展状况备受世界各国关注,人民币汇率波动备受国家和投资者关注。研究汇率的波动规律,平衡人民币国际化和人民币汇率稳定的关系,对于影响国家经济和进出口企业走势至关重要。
1 研究方法与理论分析
本节将会主要介绍文章建模所需要的ARMA模型、GARCH模型以及GARCH模型的拓展模型——TGARCH模型和EGARCH模型。
1.1 ARMA模型
由自回归模型和滑动平均模型结合而成,能够分析时间序列数据的线性部分。表达式为:
1.2 GARCH模型
GARCH模型是一种用于建模时间序列波动率的经典方法。它是对ARCH模型的扩展,能够对高阶自回归和高阶移动平均过程建模,并能够描述更复杂的异方差性质。其数学表达式为:
其中,ht表示时间t的波动率,α0表示常数项, 表示时间t - i的误差项的平方,αi和βi分别表示ARCH和GARCH过程的系数,p和q分别表示ARCH和GARCH的阶数。GARCH模型的完整表达式为:
1.3 EGARCH模型
EGARCH[1]模型,又称为指数GARCH模型,由Nelson于1991年提出,该模型的结构为:
1.4 TGARCH模型
TGARCH模型[2],又称为门限GARCH模型,它将门限自回归的概念与GARCH模型相结合所得到的GARCH模型拓展形式,其具体表达式为:
2 汇率波动性分析及预测
2.1 数据来源
本文的实证研究对象为人民币兑美元汇率中间价,下文简称“汇率”。由于2015年8月11日起,人民币兑美元中间报价机制发生改革,因此本文选取了2015年8月11日至2022年11月30日的人民币汇率数据,并去除了节假日和个别日期的缺失数据,共得到2 691个汇率数据,数据来源为Choice金融。
2.2 數据处理
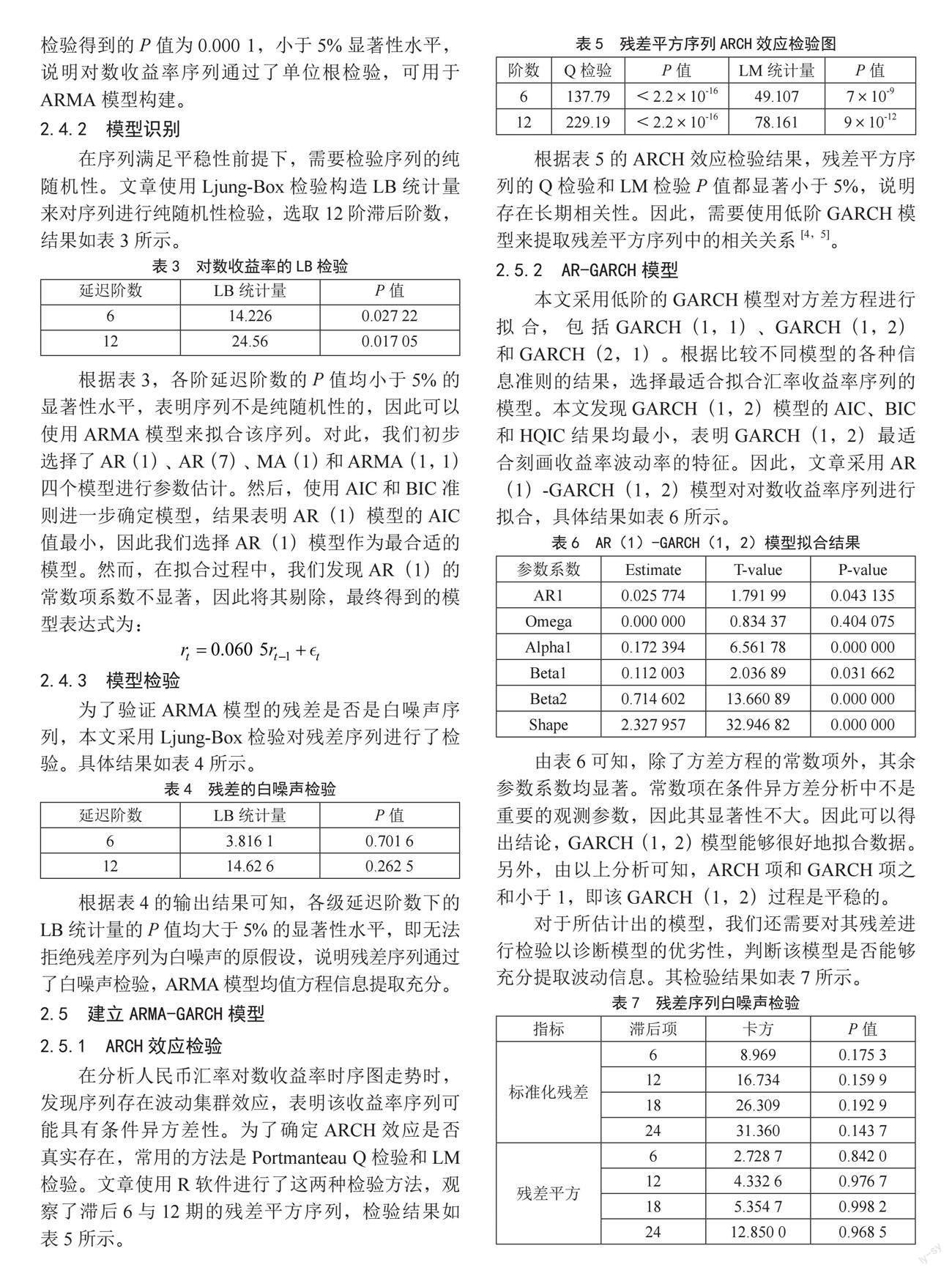
基于图1的趋势分析,可以初步推断人民币汇率原始序列存在较大波动,围绕平均值的波动情况并不稳定,这表明该序列可能是不平稳的。
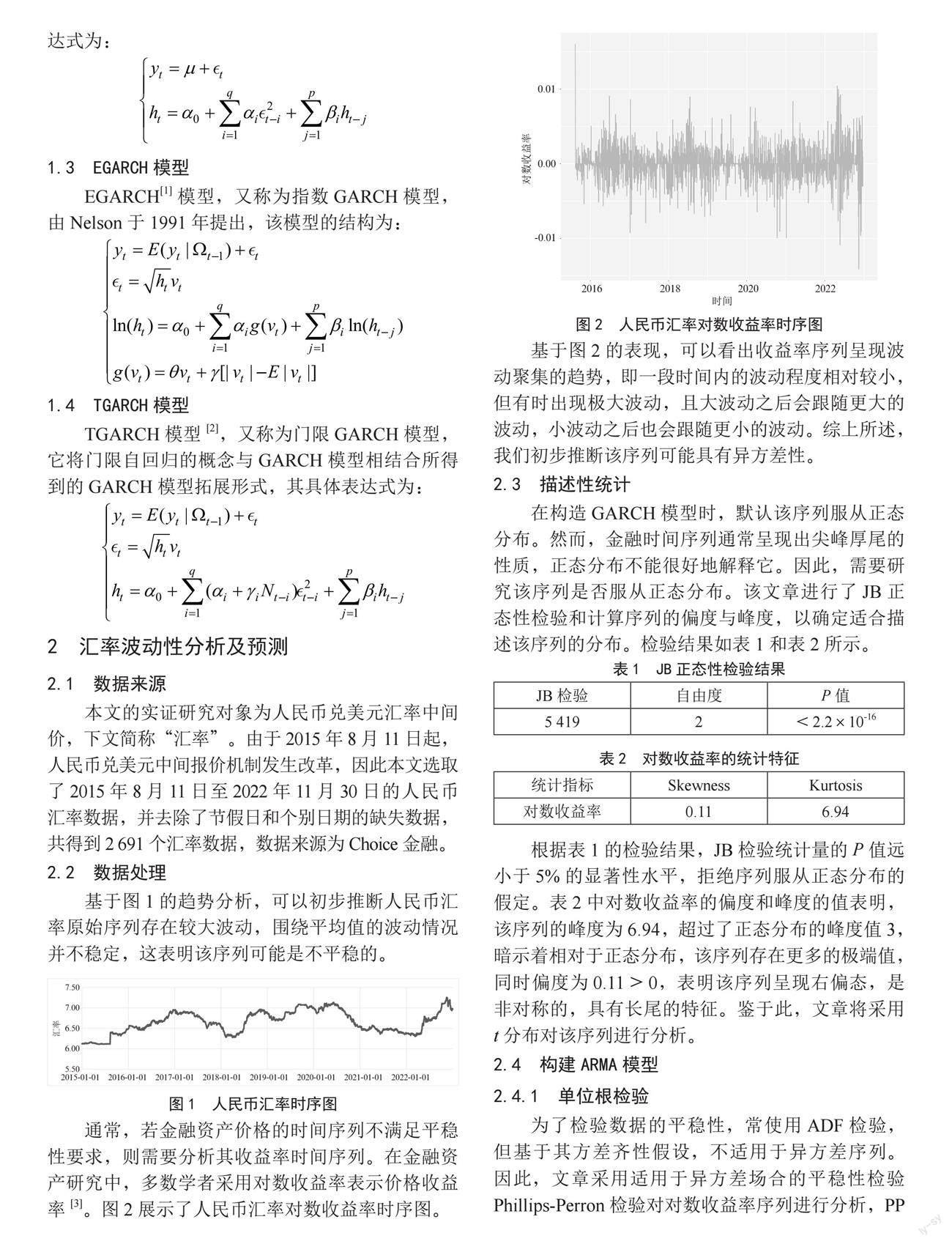
通常,若金融资产价格的时间序列不满足平稳性要求,则需要分析其收益率时间序列。在金融资产研究中,多数学者采用对数收益率表示价格收益率[3]。图2展示了人民币汇率对数收益率时序图。
基于图2的表现,可以看出收益率序列呈现波动聚集的趋势,即一段时间内的波动程度相对较小,但有时出现极大波动,且大波动之后会跟随更大的波动,小波动之后也会跟随更小的波动。综上所述,我们初步推断该序列可能具有异方差性。
2.3 描述性统计
在构造GARCH模型时,默认该序列服从正态分布。然而,金融时间序列通常呈现出尖峰厚尾的性质,正态分布不能很好地解释它。因此,需要研究该序列是否服从正态分布。该文章进行了JB正态性检验和计算序列的偏度与峰度,以确定适合描述该序列的分布。检验结果如表1和表2所示。
根据表1的检验结果,JB检验统计量的P值远小于5%的显著性水平,拒绝序列服从正态分布的假定。表2中对数收益率的偏度和峰度的值表明,该序列的峰度为6.94,超过了正态分布的峰度值3,暗示着相对于正态分布,该序列存在更多的极端值,同时偏度为0.11>0,表明该序列呈现右偏态,是非对称的,具有长尾的特征。鉴于此,文章将采用t分布对该序列进行分析。
2.4 构建ARMA模型
2.4.1 单位根检验
为了检验数据的平稳性,常使用ADF检验,但基于其方差齐性假设,不适用于异方差序列。因此,文章采用适用于异方差场合的平稳性检验Phillips-Perron检验对对数收益率序列进行分析,PP检验得到的P值为0.000 1,小于5%显著性水平,说明对数收益率序列通过了单位根检验,可用于ARMA模型构建。
2.4.2 模型识别
在序列满足平稳性前提下,需要检验序列的纯随机性。文章使用Ljung-Box检验构造LB统计量来对序列进行纯随机性检验,选取12阶滞后阶数,结果如表3所示。
根据表3,各阶延迟阶数的P值均小于5%的显著性水平,表明序列不是纯随机性的,因此可以使用ARMA模型来拟合该序列。对此,我们初步选择了AR(1)、AR(7)、MA(1)和ARMA(1,1)四个模型进行参数估计。然后,使用AIC和BIC准则进一步确定模型,结果表明AR(1)模型的AIC值最小,因此我们选择AR(1)模型作为最合适的模型。然而,在拟合过程中,我们发现AR(1)的常数项系数不显著,因此将其剔除,最终得到的模型表达式为:
2.4.3 模型检验
为了验证ARMA模型的残差是否是白噪声序列,本文采用Ljung-Box检验对残差序列进行了检验。具体结果如表4所示。
根据表4的输出结果可知,各级延迟阶数下的LB统计量的P值均大于5%的显著性水平,即无法拒绝残差序列为白噪声的原假设,说明残差序列通过了白噪声检验,ARMA模型均值方程信息提取充分。
2.5 建立ARMA-GARCH模型
2.5.1 ARCH效应检验
在分析人民币汇率对数收益率时序图走势时,发现序列存在波动集群效应,表明该收益率序列可能具有条件异方差性。为了确定ARCH效应是否真实存在,常用的方法是Portmanteau Q检验和LM检验。文章使用R软件进行了这两种检验方法,观察了滞后6与12期的残差平方序列,检验结果如表5所示。
根据表5的ARCH效应检验结果,残差平方序列的Q检验和LM检验P值都显著小于5%,说明存在长期相关性。因此,需要使用低阶GARCH模型来提取残差平方序列中的相关关系[4,5]。
2.5.2 AR-GARCH模型
本文采用低阶的GARCH模型对方差方程进行拟合,包括GARCH(1,1)、GARCH(1,2)和GARCH(2,1)。根据比较不同模型的各种信息准则的结果,选择最适合拟合汇率收益率序列的模型。本文发现GARCH(1,2)模型的AIC、BIC和HQIC结果均最小,表明GARCH(1,2)最适合刻画收益率波动率的特征。因此,文章采用AR(1)-GARCH(1,2)模型对对数收益率序列进行拟合,具体结果如表6所示。
由表6可知,除了方差方程的常数项外,其余参数系数均显著。常数项在条件异方差分析中不是重要的观测参数,因此其显著性不大。因此可以得出结论,GARCH(1,2)模型能够很好地拟合数据。另外,由以上分析可知,ARCH项和GARCH项之和小于1,即该GARCH(1,2)过程是平稳的。
对于所估计出的模型,我们还需要对其残差进行检验以诊断模型的优劣性,判断该模型是否能够充分提取波动信息。其检验结果如表7所示。
根据表7的检验结果可知,模型对水平信息以及波动信息提取均非常充分。这个AR-GARCH模型显著成立,拟合效果理想,该模型的拟合方程为:
2.5.3 AR-EGARCH模型
根据前文分析,判断人民币汇率收益率可能存在非对称性,为验证收益率的杠杆效应,需使用更贴合数据的GARCH族模型。文章首先采用EGARCH模型验证,通过比对不同模型的信息准则大小选择最适合拟合汇率收益率序列的模型得知,EGARCH(1,2)最小。因此,文章采用AR(1)-EGARCH(1,2)模型拟合对数收益率序列,结果如表8所示。
由表8可知,除了方差方程的常数项外的所有参数系数的P值均小于5%的显著性水平,均通过了显著性检验。又由于EGARCH模型的非对称性由参数αi刻画,αi为负则说明序列过程对负冲击的反应更大。而在以上的分析中,模型的系数α1为负且显著,说明对数收益率的杠桿效应存在,AR(1)-EGARCH(1,2)模型能较好地体现对数收益率的杠杆效应。
对AR(1)-EGARCH(1,2)模型拟合后显示的加权ARCH LM检验结果如表9所示。
根据表9可知,EGARCH模型拟合后的残差序列不存在ARCH效应。因此,我们最终可以确认该模型的拟合方程为:
2.5.4 AR-TGARCH模型
在本小节中文章将继续使用TGARCH模型来拟合出序列的杠杆效应,以对比EGARCH模型的效果。同样地,文章结合信息准则原理,选择合适的TGARCH模型为TGARCH(1,1)。
由表10可知,在10%的显著性水平下,该模型除了方差方程的常数项外其他系数均通过了显著性检验。同时,观察该拟合结果表可以发现,TGARCH模型的系数γ1>0且表现显著,说明对数收益率的非对称效应的存在,表明模型拟合合理。AR(1)-TGARCH(1,1)模型同样也能较好地体现对数收益率的杠杆效应。
根据表11的AR(1)-TGARCH(1,1)ARCH效应检验检验可知,TGARCH模型拟合后的残差序列不存在ARCH效应。
我们最终可以确认该模型的拟合方程为:
综上所述,由于AR-TGARCH模型在参数显著性上相对于AR-EGARCH模型表现较差,可得AR-EGARCH模型为最优拟合模型,其中,AR(1)-EGARCH(1,2)模型具有较好的解释力。
2.6 模型的拟合预测
为了检验AR-EGARCH模型有效性,本文采用回测方法:选定样本时期,使用模型预测该时间段内的VaR值,并比对真实收益率与VaR值来检验。如果有效,则落在VaR之外的样本量应与置信水平一致;无效则样本量过大,说明模型低估风险。
观察图3,圆圈圈出的地方为落在VaR曲线的样本点位置,它们大多分布在发生较大波动之前,说明该模型能在收益率发生大幅度波动之前发出相应信号,实现对波动发生的预警。由此可知,该模型的预测效果较好,具有一定的参考价值。
3 结 论
根据文章的实证分析,得出以下结论:首先,人民币汇率的对数收益率序列是平稳时间序列,呈现出明显的尖端厚尾特征,可使用t分布作为其密度分布;其次,人民币汇率的对数收益率并非纯随机过程,序列之间存在一定的相关性,可使用AR(1)模型消除其线性依赖;第三,经过ARMA模型提取了均值的序列显示出明显的条件异方差性,使用EGARCH(1,2)模型可较好地提取波动率信息。EGARCH模型方程中的杠杆效应系数小于0,说明汇率波动存在杠杆效应,且负面冲击比正面冲击对汇率的影响更大。第四,使用AR-EGARCH模型进行历史回测发现,在大幅度波动发生之前会有预警信号出现,波动并非突然发生。
基于以上研究,提出以下建议:首先,政府部门应积极适度地干预汇率变动,维护外汇市场交易秩序的稳定和汇率的平稳;其次,应权衡人民币国际化与汇率稳定的关系,在人民币国际化的进程中扩大外汇市场对内对外开放,鼓励“走出去”“迎进来”战略,降低人民币升值的预期,缓和杠杆效应中的负面冲击。当汇率波动增大时,应适当放缓人民币国际化的步伐,维护汇率稳定。
参考文献:
[1] 朱信凯,韩磊,曾晨晨.信息与农产品价格波动:基于EGARCH模型的分析 [J].管理世界,2012(11):57-66+188.
[2] 谢赤,禹湘,储慧斌.基于TGARCH模型的证券投资惯性反向交易策略实证研究 [J].管理科学,2007(3):68-75.
[3] TSAY R S.金融时间序列分析 [M].王远林,王辉,潘家柱,译.北京:人民邮电出版社,2012:1-129.
[4] 刘潭秋.人民币实际汇率的非线性特征研究 [J].数量经济技术经济研究,2007(2):11-18.
[5] 沙文兵,刘红忠.人民币国际化、汇率变动与汇率预期 [J].国际金融研究,2014(8):10-18.
作者简介:蔡斌坚(2001—),男,汉族,广东潮州
人,本科在读,研究方向:时间序列分析。
