利用体积分方程的弱化BCGS算法模拟各向异性地层中多分量低频海洋可控源电磁响应
2023-09-05魏宝君刘莹刘健李静陈涛边旭
魏宝君 刘莹 刘健 李静 陈涛 边旭


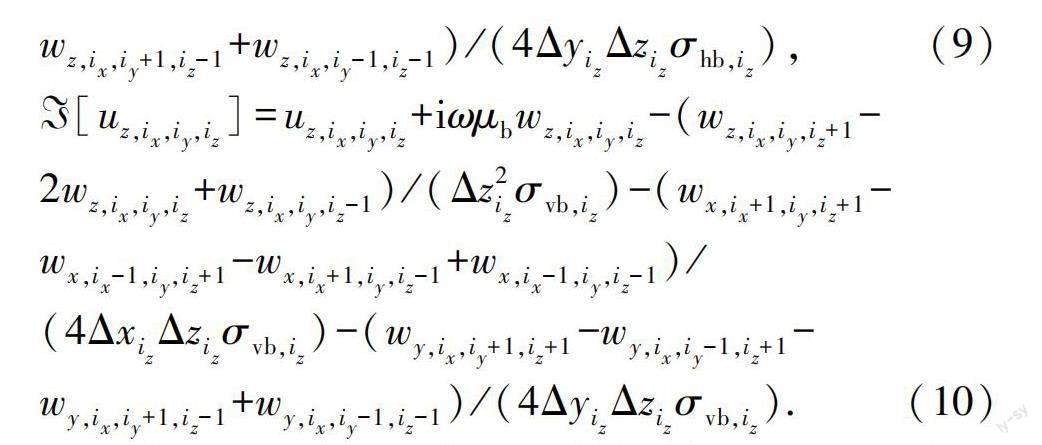
摘要:基于層状单轴各向异性介质的并矢Green函数和体积分方程的弱化稳定型双共轭梯度(BCGS)算法模拟各向异性背景地层中多分量低频海洋可控源电磁响应,并通过算例分析发射频率、海底背景地层各向异性和异常体埋藏深度对响应的影响特征。结果表明:发射信号的不同频率、电场强度的不同分量对海底油气藏的水平分辨能力不同;当测线沿x方向布设时,Ezz分量的分辨能力最强,Exx分量次之,Eyy分量的水平分辨能力最低;在海底背景地层水平电导率相同的情况下,背景地层垂向电导率的变化对Exx分量和Ezz分量的影响规律不同,而Eyy分量基本不受地层垂向电导率变化的影响;异常体埋藏深度越浅,Exx分量和Ezz分量对异常体的水平分辨能力越高,而无论异常体埋藏深浅Eyy分量均不能对其进行分辨。
关键词:体积分方程; 海洋可控源电磁; 各向异性; 多分量
中图分类号:P 631.9 文献标志码:A
引用格式:魏宝君,刘莹,刘健,等.利用体积分方程的弱化BCGS算法模拟各向异性地层中多分量低频海洋可控源电磁响应[J].中国石油大学学报(自然科学版),2023,47(1):62-73.
WEI Baojun, LIU Ying, LIU Jian, et al. Simulating multi-component low-frequency MCSEM responses in anisotropic formation using weak-form BCGS algorithm for volume integral equations[J]. Journal of China University of Petroleum (Edition of Natural Science), 2023,47(1):62-73.
Simulating multi-component low-frequency MCSEM responses
in anisotropic formation using weak-form BCGS algorithm
for volume integral equations
WEI Baojun, LIU Ying, LIU Jian, LI Jing, CHEN Tao, BIAN Xu
(College of Science in China University of Petroleum (East China), Qingdao 266580, China)
Abstract:The multi-component low-frequency marine controlled-source electromagnetic(MCSEM) responses in anisotropic background formation were simulated based on dyadic Green's functions for stratified uniaxial anisotropic medium and weak-form BCGS algorithm for volume integral equations. The influence of the transmitter frequency, anisotropy in the submarine background formation and the depth of the abnormal body were analyzed by numerical models. The results show that different frequencies of the transmitter and different components of the electric field have different horizontal resolutions for detecting the submarine oil reservoir. When the survey line is disposed alone x-direction, the resolving ability of the Ezz-component is most powerful, the Exx-component comes second, and the Eyy-component has lowest resolution ability. On the condition of the same horizontal conductivity of the submarine background formation, changes in the vertical conductivity of the background formation have different influences on Exx-component and Ezz-component, while the Eyy-component keeps unchanged. The horizontal resolving ability of Exx-component and Ezz-component become higher when the depth of the abnormal body becomes shallower, while the Eyy-component cannot resolve the abnormal body no matter whether the depth is shallow or deep.
Keywords: volume integral equations; MCSEM (marine controlled-source electromagnetic); anisotropy; multi-component
海洋可控源电磁(marine controlled-source electromagnetic,简称MCSEM)探测技术通过人工发射源在海底发射和接收低频电磁波以获取海底地层电阻率信息,从而达到识别高阻油气藏的目的,是一种与海洋地震勘探技术互补的海洋油气勘探技术,近几年获得了迅猛发展并被逐渐广泛采用[1-5]。数值模拟方法尤其是三维正演算法对于MCSEM仪器的研发、探测特性分析和海洋电磁数据的处理解释具有重要意义。可用于模拟三维MCSEM响应的算法比较多,主要包括有限元素法[2,4,6-9]、有限差分法[1,10]和体积分方程法[11-16]等。与有限元素法和有限差分法需要在全空间进行数据离散和求解相比,体积分方程的数据点只分布在三维异常体所处的区域,未知量数目和计算量均大大减少,根据需要既可以完全求解也可以近似求解,因此该方法一直是计算三维电磁响应的重要方法。需要指出的是,除个别文献在模拟可控源大地电磁响应时考虑到地层的各向异性外[15],目前应用体积分方程法求解三维电磁波问题主要集中在各向同性地层,而在海洋环境中海底地层因受沉积因素等影响呈现出各向异性特征[7],因此在用体积分方程法模拟三维MCSEM响应时需要考虑到背景地层和异常体的各向异性。笔者基于层状单轴各向异性介质并矢Green函数的递推矩阵算法[17]和体积分方程的弱化稳定型双共轭梯度(BCGS)算法[14,18-19],将二者有机结合,模拟各向异性地层中多分量低频MCSEM的响应,分析发射频率、海底背景地层各向异性、异常体埋深等因素对不同分量MCSEM响应的影响规律。
1 基本理论
1.1 层状各向异性地层中的体积分方程
所采用的坐标系和地层模型如图1所示,其中xyz为地层直角坐标系,其z轴为地层界面法线方向,三分量发射天线和接收天线分别沿x、y和z方向。该模型既包含水平层状单轴各向异性背景地层,也包含各向異性电导率异常体。背景地层的电导率张量为σb=diag(σhb,σhb,σvb),其中σhb为背景地层的水平电导率,σvb为背景地层的垂直电导率,不同的背景地层其电导率张量不同,异常体的电导率张量σ=[σij]为3×3阶矩阵。由于所采用的频率较低,在体积分方程中忽略位移电流的影响。将多分量低频电磁探测仪器的所有发射天线视为电偶极子,并假设发射源随时间的变化关系为exp(iωt),其中ω为角频率,则接收天线处的电场强度矢量可表示为如下体积分方程形式:
式中,rT、rR分别为发射天线和接收天线的位置坐标;D为包含电导率异常体的积分区域;GEJ(rR,r′)为层状各向异性背景地层中r′处的单位电流元在接收点rR处的电型并矢Green函数[17];Δσ(r′)=σ(r′)-σb(r′)为异常体与背景地层电导率张量之差;E(r′,rT)为发射天线在积分区域内产生的总电场强度;Eb(rR,rT)为发射天线在层状各向异性背景地层中产生的电场强度,可由层状各向异性介质中的电流源电型并矢Green函数GEJ(rR,rT)得到。式(1)称为数据方程,若积分区域内总电场强度E(r′,rT)的分布已知,由该式可获得接收天线处的电场强度。
在积分区域D内,总电场强度矢量E(r,rT)满足如下体积分方程:
式(2)的形式同式(1),只不过该式接收位置在积分区域D内。式(2)称为目标方程,是计算异常体内总电场分布的第二类Fredholm积分方程。
由于GEJ(r,r′)在r=r′处存在强奇异性,在积分区域D内不能直接求解式(2),而是根据GEJ与GAJ所满足的如下关系:
求解其等价形式的体积分方程:
式中,GAJ(r,r′)为层状各向异性背景地层中r′处的单位电流元在场点r处的磁矢势并矢Green函数[17]。由于GAJ的奇异性大大降低,并且对其含奇异点的积分可以进行弱化处理,故求解式(3)可避免奇异值的出现。
将积分区域D离散为N个立方体形小单元Dj(j=1,2,…,N),每个小单元的体积为ΔVj。假设在每个小单元内异常体与背景地层的电导率张量之差恒定,设为Δσj,并假设在每个小单元内电场强度值恒定且由其中心点的值代替,则式(1)可离散为
式(3)的离散形式为
式(5)可表示为如下线性形式:
其中I为线性算子,定义为
其中
设第i个小单元在地层直角坐标系中沿x、y、z三个方向的编号分别为ix、iy、iz(ix=1,2,…,Nx,iy=1,2,…,Ny,iz=1,2,…,Nz,则N=NxNyNz),并假设具有相同垂向编号iz的所有小单元的尺寸均相同,其边长分别记为Δxiz、Δyiz、Δziz,则式(7)可以展开为如下形式:
式(6)可采用稳定型双共轭梯度(BCGS)方法进行迭代求解[18],从而得到总电场强度在异常区域D内的分布。求解式(6)时先给定异常区域内总电场强度的任意初始猜测值E0(例如E0=0),并计算下列残差:
当║s║/║Eb║或║rk║/║Eb║小于给定的迭代误差时,迭代终止。将采用上述算法得到的总电场强度E(ri,rT)代入式(4),即可得到接收天线处的电场强度在地层直角坐标系中的各个分量。
1.2 层状各向异性背景地层的并矢Green函数
设多分量低频海洋可控源电磁探测仪器各分量发射天线的电偶极矩为PT,則发射天线在海底背景地层中产生的电场强度的各分量可表示为
在积分区域D内计算式(6)须针对所有小单元计算磁矢势并矢Green函数GAJ的体积分∫DjGAJ(ri,r′)dr′。选
GAJ为如下形式[17]:
并且有GAJxx=GAJyy。GAJ由背景项和散射项这两部分构成,即GAJ=PGAJ+SGAJ。由于散射项SGAJ不含奇异点,故对SGAJ的数值积分可近似表示为
若源点r′和场点ri不在同一背景地层中,则GAJ只包含散射项SGAJ。若源点r′和场点ri在同一背景地层中,GAJ除包含散射项外还包含背景项PGAJ。若r′和ri虽在同一背景地层但i≠j,即ri不在小单元Dj内,则对PGAJ的积分不存在奇异值问题,可近似为
若i=j,即源点r′和场点ri在同一个小单元Dj内,则对PGAJ的积分存在奇异值问题,需进行弱化处理。PGAJ各分量的具体表达式为
其中
式中,Kb为背景地层的各向异性系数。
对于式(14)和式(15)的积分,由于被积函数在小单元Dj内是相对于中心点rj的奇函数,故有
在计算体积分方程时,SGAJ的计算是非常耗时的。由于SGAJ是3个独立的Sommerfeld积分的组合,而这些Sommerfeld积分只依赖于、z和z′,并不直接依赖于x、x′、y或y′,所以只需根据不同的、z和z′预先计算和存储这些Sommerfeld积分,在针对所有小单元计算SGAJ时将其进行组合和插值即可,从而达到节约计算时间和内存的目的。
2 数值模拟
2.1 算法验证
采用文献[16]提供的半空间各向同性地层中存在相对高电导率块状异常体的大地电磁测量模型验证所开发算法的正确性。如图2所示,电导率为0.2 S·m-1的异常体位于均匀半空间的各向同性地层中,背景地层的电导率为0.02 S·m-1,异常体的尺寸为120 m×200 m×400 m,异常体中心点的坐标为(1000 m,0 m,300 m)。在地面沿x方向布设有限长的线电流源,发射源的长度为100 m,中心点坐标为(50 m,0 m,0 m),发射电流强度为1 A,发射频率为3 Hz。沿x方向布设一条测线,测线的起始位置为(400 m,0 m,0 m),终点位置为(1400 m,0 m,0 m)。采用体积分方程模拟时在异常体上所取的小单元的尺寸为20 m×20 m×20 m,故小单元数目为N=6×10×20=1200。
将采用上述体积分方程模拟得到的总电场强度Exx(下角标“xx”表示沿x方向发射源产生的电场强度的x分量,下同)和由异常体产生的散射场ESxx随接收天线横向位置xR的变化关系与文献[16]给出的非结构化有限元的模拟结果进行对比,对比曲线见图3。由图3可以看出,无论是总场还是散射场,上述体积分方程的计算结果(标记为VIE)均与文献[16]的结果(标记为FEM)高度吻合,验证了本文中体积分方程弱化BCGS算法的正确性。另由图3的计算结果可知,当接收天线到达异常体上方时,总电场强度的实部和虚部均出现下凹现象,数值变小。这是由于低电导率背景地层中相对高电导率异常体的存在使得感应电流更趋向于向高电导率异常体所处的区域流动,导致地面附近的电流密度降低。利用Exx曲线的这个特点可以对地层中异常体的存在与否、异常体电导率的相对高低及横向位置做出判断。
2.2 发射频率对多分量MCSEM响应的影响
考虑到海底油气藏的电导率低于海底背景地层的电导率,在分析发射频率对MCSEM不同分量响应的影响规律时采用如图4所示的三维海洋电磁探测模型。电导率为0.06 S·m-1的相对低电导率块状异常体位于海底的各向异性地层中,海水的电导率为4 S·m-1,海底背景地层的水平电导率为1 S·m-1、垂向电导率为0.8 S·m-1,异常体的尺寸、中心点坐标和小单元数目同图2所示模型。电流强度为1 A的单位长度三分量线电流源T位于海底上方,坐标为(50 m,0 m,-10 m)。三分量接收天线R位于海底表面且沿x方向布设,起始测量位置为(400 m,0 m,0 m),终点测量位置为(1400 m,0 m,0 m)。取发射频率分别为0.5、1和5 Hz,采用上述体积分方程模拟3个主分量电场强度Exx、Eyy和Ezz的背景场、总场和由异常体产生的散射场随接收天线横向位置xR的变化关系,计算结果分别见图5和图6。
由图5(a)可知,当频率为0.5 Hz时Exx分量实部信号的强度较大,随着频率的升高,由于电磁信号在地层中的衰减加剧,信号的强度逐渐变小。在接收天线逐渐远离发射天线的过程中,各频率信号的强度逐渐变小且频率为5 Hz的信号出现过零点现象。当接收天线到达异常体上方时,Exx分量總场和背景场的实部曲线开始出现分离,总场强度大于背景场强度。这是由于高电导率背景地层中相对低电导率异常体的存在使得沿x方向的感应电流更趋向于避开异常体所处的区域流动,导致海底表面附近电流密度升高。当频率为0.5 Hz时,Exx分量总场和背景场实部曲线的分离不明显,异常体产生的散射信号相对较弱;当频率为1 Hz时,由于异常体产生的散射信号强度变化不大(图6(a))而背景场信号强度变小,Exx分量总场和背景场实部曲线的分离较为明显;当频率升高到5 Hz时,由于背景场信号和异常体产生的散射信号的强度均明显变小(图6(a)),曲线分离程度与频率为1 Hz的情况差别不大。根据图5(a)和图6(a)的模拟结果,综合考虑信号衰减因素和对电导率异常体的分辨能力,选择1 Hz的发射频率要优于0.5 和5 Hz的发射频率。由图5(b)可知,3种频率下Exx分量背景场和总场的虚部曲线均比较接近,对电导率异常体的分辨能力较低。
由图5(c)可知,当接收天线到达异常体上方时,除频率为0.5 Hz的信号外,1和5 Hz频率Eyy分量总场和背景场的实部曲线均出现分离现象,但由于数据分离仅出现在过零点附近,因数值太小而不易区分。由图5(d)可知,3种频率下Eyy分量背景场和总场的虚部曲线均未出现明显的分离现象,不能分辨出电导率异常体。总体而言,Eyy分量对电导率异常体的分辨能力极低,远低于Exx分量。
由图5(e)和(f)可以看出,当接收天线到达异常体上方时,3种频率情况下Ezz分量总场和背景场的实部、虚部曲线均出现分离现象,电导率异常体的影响明显。与图5(a)中Exx实部曲线不同的是,Ezz总场和背景场曲线仅在异常体所处的区域范围内出现分离,而Exx总场和背景场实部曲线在接收天线跨越异常体后仍然分离,相比较而言Ezz曲线的水平分辨能力更高。这是由于地层中沿x方向的感应电流在避开相对低电导率异常体向海底表面附近流动后,仍会在异常体后方相当大的水平范围内继续在海底表面附近沿x方向流动,而沿z方向的感应电流仅在相对低电导率异常体上方的区域及其附近避开异常体并沿其侧面流动,跨过异常体后就不再受其影响。图5(e)与图5(a)的另一个不同之处就是在曲线分离区域内Ezz分量的总场强度小于背景场强度,这与图5(a)的结果正好相反。这是由于沿z方向的感应电流在相对低电导率异常体上方会避开异常体流动,从而导致异常体上方海底表面附近的电流密度降低。对比图5不同分量总场和背景场的曲线可以看出,Ezz曲线的水平分辨能力最高,Exx曲线次之,Eyy曲线的水平分辨能力最低。
由图6给出的散射电场曲线可以发现,频率为5 Hz的散射场信号最弱,频率为0.5 和1 Hz的散射场信号较强,再考虑到不同频率的电磁场总信号在导电媒质中的衰减程度不同,在这3种频率中选择1 Hz的发射频率探测效果最佳。综合对图5和6的分析可以看出,MCSEM探测技术中发射信号的不同频率、电场强度的不同分量对异常体的水平分辨能力不同,可以综合利用多频率、多分量电磁场信息实现对海底油气藏目标更加全面和准确的识别。
2.3 海底地层各向异性对多分量MCSEM响应的影响
在分析海底地层各向异性对MCSEM不同分量响应的影响规律时仍采用如图4所示的三维海洋电磁模型。取发射频率为1 Hz,海底背景地层的水平电导率固定为1 S·m-1,垂向电导率可变,其余参数同上。取海底背景地层的垂向电导率分别为0.5、0.6和0.8 S·m-1,即各向异性系数K2b分别为2.0、1.67和1.25,采用上述体积分方程模拟3个主分量电场强度Exx、Eyy和Ezz的总场和散射场的幅度随接收天线横向位置xR的变化关系,计算结果见图7。
由图7(a)可以看出,当接收天线与发射天线的水平距离较近时,海底背景地层各向异性的差异对Exx总场幅度的影响可以忽略,对Exx信号的贡献主要来自于背景地层的水平电导率。随着沿x方向发射—接收距离的增大,海底背景地层垂向电导率的影响逐渐增加,不同的各向异性系数对应的Exx总场幅度曲线开始分离,背景地层的垂向电导率越低,对Exx信号产生的衰减作用越弱,Exx信号的强度越大。在接收天线靠近和到达异常体上方后,由于散射场变强,总电场强度的幅度曲线出现上凸现象,高于背景场曲线(参考图5(a),就海底油气藏这种低电导率异常体情况而言,Exx总场幅度大于背景场幅度)。由图7(b)可知,异常体产生的Exx分量的散射场受海底地层各向异性的影响较大,且关系复杂。在异常体上方区域范围内,K2b=2.0对应的散射场最强,K2b=1.67对应的散射场最弱,而K2b=1.25对应的曲线则介于二者之间,从而使K2b=1.67的曲线对低电导率异常体的水平分辨能力较另两条曲线低。
由图7(c)可以看出,无论发射—接收距离是近是远,无论接收天线是否在异常体上方,3条曲线均基本重合,海底背景地层各向异性的差异对Eyy总场幅度的影响可以忽略,电导率异常体的存在也没有对Eyy分量产生影响。由于接收天线是沿x方向布设,接收天线和发射天线沿x方向的相对位置在改变,而它们沿y方向的坐标始终相同(即yR=yT),因而当沿x方向的发射—接收距离逐渐增大时,Eyy曲线呈现出与Exx曲线不同的变化特征。无论海底背景地层各向异性的差异是大是小,Eyy曲线对电导率异常体的分辨能力均为最弱。
由图7(e)可以看出,无论发射—接收距离是近是远,海底背景地层各向异性的差异对Ezz总场幅度的影响始终存在。背景地层的垂向电导率越低,Ezz信号的强度越小,这与图7(a)远距离的情况恰好相反。这是由于在3个主分量中Ezz分量的背景场受背景地层垂向电导率的影响最大,因此当背景地层的垂向电导率发生变化时Ezz分量的背景场也将改变。再考虑到散射场与海底地层的各向异性有关(图7(f)),因此Ezz分量的总场始终受地层各向异性的影响。另由图7(f)可知,异常体产生的Ezz分量的散射场受海底地层各向异性的影响规律也较复杂。与图7(b)类似,在异常体上方区域范围内,K2b=1.67对应的散射场最弱,从而使图7(e)中K2b=1.67对应的Ezz曲线对低电导率异常体的水平分辨能力较另两条曲线低。
综合考察图7可以看出,在海底背景地层水平电导率相同的情况下,背景地层不同的各向异性系数对Exx分量和Ezz分量的影响规律不同,而Eyy分量基本不受地层各向异性系数的影响且水平分辨能力最低。
2.4 异常体埋深对多分量MCSEM响应的影响
在分析异常体埋深对MCSEM不同分量响应的影响规律时仍采用如图4所示的模型。取发射频率为1 Hz,海底背景地层的水平电导率为1 S·m-1、垂向电导率为0.8 S·m-1,其余参数同上。取异常体顶部到海底地层表面的距离分别为50、100和200 m,采用上述体积分方程模拟3个主分量电场强度Exx、Eyy和Ezz的总场和散射场的幅度随接收天线横向位置xR的变化关系,计算结果见图8。
由图8可知,当异常体顶部到海底地层表面的距离为较浅的50 m时,由于异常体产生的散射场最强,Exx分量和Ezz分量对低电导率异常体的水平分辨能力最高。如前所述,在曲线分离区域内两个分量的变化正好相反,一个出现上凸现象,一个出现下凹现象。随着异常体埋藏深度的增加,散射场越来越弱,Exx和Ezz分量对异常体的水平分辨能力逐渐降低,当异常体顶部达到200 m深度时已不能分辨,此时总场幅度曲线与背景场幅度曲线基本重合。无论异常体埋藏深浅,Eyy分量均不能分辨出异常体的存在。
3 结 论
(1)在MCSEM探测中电场强度的不同分量对海底油气藏的水平分辨能力不同。当测线沿x方向布设时,Ezz分量的分辨能力最强,Exx分量次之,Eyy分量的水平分辨能力最低。发射信号的频率不同,MCSEM探测技术的水平分辨能力也不同。由于不同频率下异常体散射场信号的强弱不同,電磁场总信号在导电媒质中的衰减程度不同,因而针对海底某种异常体分布存在最佳频率范围。在实际MCSEM探测中可以综合利用多频率、多分量电磁场信息实现对海底油气藏目标更加全面和准确的识别。
(2)对海底油气藏这种相对低电导率异常体的分布而言,当接收天线在异常体上方的海底表面沿x方向进行探测时,Exx分量的总场强度大于背景场强度,而Ezz分量的总场强度小于背景场强度。
(3)在海底背景地层水平电导率相同的情况下,背景地层不同的各向异性系数对Exx分量和Ezz分量的影响规律不同,而Eyy分量基本不受地层各向异性系数的影响且水平分辨能力最低。
(4)异常体埋深越浅,Exx分量和Ezz分量对低电导率异常体的水平分辨能力越高。随着异常体埋藏深度的增加,两个分量的分辨能力逐渐降低。无论异常体埋藏深浅,Eyy分量均不能分辨出异常体的存在。
参考文献:
[1]殷长春,贲放,刘云鹤,等.三维任意各向异性介质中海洋可控源电磁法正演研究[J].地球物理学报,2014,57(12):4110-4122.
YIN Changchun, BEN Fang, LIU Yunhe, et al. MCSEM 3D modeling for arbitrarily anisotropic media[J]. Chinese Journal of Geophysics, 2014,57(12):4110-4122.
[2]杨军,刘颖,吴小平.海洋可控源电磁三维非结构矢量有限元数值模拟[J].地球物理学报,2015,58(8):2827-2838.
YANG Jun, LIU Ying, WU Xiaoping. 3D simulation of marine CSEM using vector finite element method on unstructured grids[J]. Chinese Journal of Geophysics, 2015,58(8):2827-2838.
[3]罗鸣,李予国.一维电阻率各向异性对海洋可控源电磁响应的影响研究[J].地球物理学报,2015,58(8):2851-2861.
LUO Ming, LI Yuguo. Effects of the electric anisotropy on marine controlled-source electromagnetic responses[J]. Chinese Journal of Geophysics, 2015,58(8):2851-2861.
[4]陈汉波,李桐林,熊彬,等.基于微增模型的海洋可控源电磁法三维非结构化矢量有限元数值模拟[J].地球物理学报,2018,61(6):2560-2577.
CHEN Hanbo, LI Tonglin, XIONG Bin, et al. 3D MCSEM modeling using an edge-based finite element method based on an unstructured grid and incremental model[J]. Chinese Journal of Geophysics, 2018,61(6):2560-2577.
[5]刘健,王江涛,王子鸣,等.洋流和潮波产生的感应电磁场的对比研究[J].中国石油大学学报(自然科学版),2022,46(4):52-62.
LIU Jian, WANG Jiangtao, WANG Ziming, et al. Comparative research on induced electromagnetic fields generated by ocean current and tidal wave[J]. Journal of China University of Petroleum (Edition of Natural Science), 2022,46(4):52-62.
[6]SCHWARZBACH C, BORNER R U, SPITZER K. Three-dimensional adaptive higher order finite element simulation for geo-electromagnetics—a marine CSEM example[J]. Geophysical Journal International, 2011,187(1):63-74.
[7]蔡紅柱,熊彬,ZHDANOV M.电导率各向异性的海洋电磁三维有限单元法正演[J].地球物理学报,2015,58(8): 2839-2850.
CAI Hongzhu, XIONG Bin, ZHDANOV M. Three-dimensional marine controlled-source electromagnetic modeling in anisotropic medium using finite element method[J]. Chinese Journal of Geophysics, 2015,58(8):2839-2850.
[8]叶益信,李予国,刘颖,等.基于局部加密非结构网格的海洋可控源电磁法三维有限元正演[J].地球物理学报,2016,59(12):4747-4758.
YE Yixin, LI Yuguo, LIU Ying, et al. 3D finite element modeling of marine controlled-source electromagnetic fields using locally refined unstructured meshes[J]. Chinese Journal of Geophysics, 2016,59(12):4747-4758.
[9]邱长凯,殷长春,刘云鹤,等.任意各向异性介质中三维可控源音频大地电磁正演模拟[J].地球物理学报,2018,61(8):3488-3498.
QIU Changkai, YIN Changchun, LIU Yunhe, et al. 3D forward modeling of controlled-source audio-frequency magnetotellurics in arbitrarily anisotropic media[J]. Chinese Journal of Geophysics, 2018,61(8):3488-3498.
[10]STREICH R. 3D finite-difference frequency-domain modeling of controlled-source electromagnetic data: direct solution and optimization for high accuracy[J]. Geophysics, 2009,74(5):F95-F105.
[11]WANNAMAKER P E, HOHMANN G W, SANFILIPO W A. Electromagnetic modeling of three-dimensional bodies in layered earths using integral equations[J]. Geophysics, 1984,49(1):60-74.
[12]AVDEEV D B, KUVSHINOV A V, PANKRATOV O V, et al. Three-dimensional induction logging problems, Part I: an integral equation solution and model comparisons[J]. Geophysics, 2002,67(2):413-426.
[13]MILLARD X, LIU Q H. Simulation of near-surface detection of objects in layered media by the BCGS-FFT method[J]. IEEE Trans Geosci Remote Sensing, 2004,42(2):327-334.
[14]WEI B J, SIMSEK E, LIU Q H. Improved diagonal tensor approximation (DTA) and hybrid DTA/BCGS-FFT method for accurate simulation of 3D inhomogeneous objects in layered media[J]. Waves in Random and Complex Media, 2007,17(1):55-66
[15]陈桂波,汪宏年,姚敬金,等.用积分方程法模拟各向异性地层中三维电性异常体的电磁响应[J].地球物理学报,2009,52(8):2174-2181.
CHEN Guibo, WANG Hongnian, YAO Jingjin, et al. Modeling of electromagnetic response of 3-D electrical anomalous body in a layered anisotropic earth using integral equations[J]. Chinese Journal of Geophysics, 2009,52(8):2174-2181.
[16]湯井田,周峰,任政勇,等.复杂地下异常体的可控源电磁法积分方程正演[J].地球物理学报,2018,61(4):1549-1562.
TANG Jingtian, ZHOU Feng, REN Zhengyong, et al. Three-dimensional forward modeling of the controlled-source electromagnetic problem based on the integral equation method with an unstructured grid[J]. Chinese Journal of Geophysics, 2018,61(4):1549-1562.
[17]WEI B J, ZHANG G J, LIU Q H. Recursive algorithm and accurate computation of dyadic Green's functions for stratified uniaxial anisotropic media[J]. Science in China: Series F, 2008,51(1):63-80.
[18]魏宝君, LIU Q H. 层状介质中计算体积分方程的弱化BCGS-FFT算法[J]. 中国石油大学学报(自然科学版), 2007,31(1):49-55.
WEI Baojun, LIU Q H. Weak-form BCGS-FFT algorithm for volume integral equations in stratified medium[J]. Journal of China University of Petroleum (Edition of Natural Science), 2007,31(1):49-55.
[19]魏宝君,LIU Q H.水平层状介质中基于DTA的三维电磁波逆散射快速模拟算法[J]. 地球物理学报, 2007,50(5):1595-1605.
WEI Baojun, LIU Q H. Fast algorithm for simulating 3-D electromagnetic inverse scattering in horizontally stratified medium via DTA[J]. Chinese Journal of Geophysics, 2007,50(5):1595-1605.
(编辑 修荣荣)
