圆渐开线变截面涡旋压缩机型线的参数优化

彭 斌, 陶耀辉, 刘慧鑫

(兰州理工大学 机电工程学院,甘肃 兰州 730050)

涡旋压缩机因效率高、噪声低、振动小、体积小等优点而被广泛应用于制冷、空调等领域。变截面涡旋压缩机由于能以较少的圈数实现高压缩比的优势,一直是研究的热点。文献[1]对变径基圆渐开线涡旋盘的结构进行了优化;文献[2]基于控制体积法建立了变壁厚涡旋压缩机的几何模型;文献[3]对变截面涡旋压缩机的结构及其性能优势进行了分析;文献[4]提出一种圆渐开线-高次曲线-圆弧组合的变截面型线,构建了涡旋压缩机的整体数学模型并进行了试验研究;文献[5]利用变径基圆构建了一种变壁厚涡旋齿,改善了涡旋齿的受力变形,得到在介质压力作用下的应力分布及变形规律;文献[6]基于泛函理论对变壁厚涡旋型线进行优化,建立了优化数学模型,得到了优化型线;文献[7]利用NSGA-Ⅱ算法对变截面涡旋压缩机进行了优化,并对优化模型与传统变截面涡旋盘进行了对比;文献[8]基于Frenet标架建立了圆渐开线变截面压缩机的数学模型,推导了工作腔容积计算公式,并对传统变截面涡旋压缩机做了定量分析;文献[9]提出一种新型圆渐开线变截面涡旋齿构建理论,并给出了通用模型几何参数;文献[10]分析了圆渐开线变截面涡旋压缩机的几何性能;文献[11]利用MATLAB遗传算法工具箱优化了圆渐开线截面涡旋盘的几何性能;文献[12]利用遗传算法对2种变截面涡旋盘的几何性能进行了优化,并得出优化后涡旋盘几何参数的非劣解集。

圆渐开线变截面涡旋压缩机几何性能优异,在压缩比、行程容积和面积利用系数方面比其他变截面涡旋压缩机优势更大。在圆渐开线变截面涡旋压缩机的优化方面,只考虑了几何性能的优化,忽略了力学性能对涡旋压缩机的影响,而涡旋压缩机所受气体力是引起压缩机振动、噪声和泄漏的一个主要原因,尤其当涡旋压缩机所受的轴向气体力过大时,会增大压缩机的轴向间隙,使径向泄漏量增加,严重影响压缩机的性能。因此有必要对涡旋压缩机进行几何性能和力学性能的综合优化,以构建在压缩比和轴向气体力方面都有优势的圆渐开线变截面涡旋机。

1 型线母线的建立

涡旋齿的母线由3段圆渐开线组成,其中第1段渐开线和第3段渐开线的基圆半径相同,第2段渐开线基圆半径比其余2段渐开线的基圆半径大。

第1段圆渐开线母线方程如下:

(1)

第2段圆渐开线母线方程如下:

(2)

第3段圆渐开线母线方程如下:

(3)

为保证型线的连续性和光滑性,曲率半径需满足以下条件:

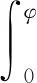
(4)

(5)

(6)

其中:φ1为第1段圆渐开线最大展角;φ2为第2段圆渐开线最大展角;φe为第3段圆渐开线最大展角;a为第1段和第3段圆渐开线基圆半径;a1为第2段圆渐开线基圆半径。为方便计算取x0(φ0)=a、y0(φ0)=0。

由渐开线母线方程生成的母线如图1所示。

图1 圆渐开线变截面涡旋齿母线

利用法向等距线法[13]由母线生成圆渐开线变截面涡旋齿,对生成的变截面涡旋齿的齿头采用双圆弧修正,双圆弧修正过程如图2所示。

图2 双圆弧修正

图2中:γ为修正角;φ为修正展角;λ为圆弧中心角;β为修正底角;Rd、Rx分别为大、小圆弧半径。以上参数中只有1个参数是独立的,只要确定1个,即可确定出其他参数。其中γ、λ、φ、β的关系为:

γ=φ-λ+π/2

(7)

λ=π-2β

(8)

φ=cotβ-π/2

(9)

修正后的圆渐开线变截面涡旋齿如图3所示。

2 优化数学模型的构建

2.1 压缩腔容积计算

圆渐开线变截面涡旋压缩机腔体如图4所示,由内到外分别是第1压缩腔、第2压缩腔和第3压缩腔。

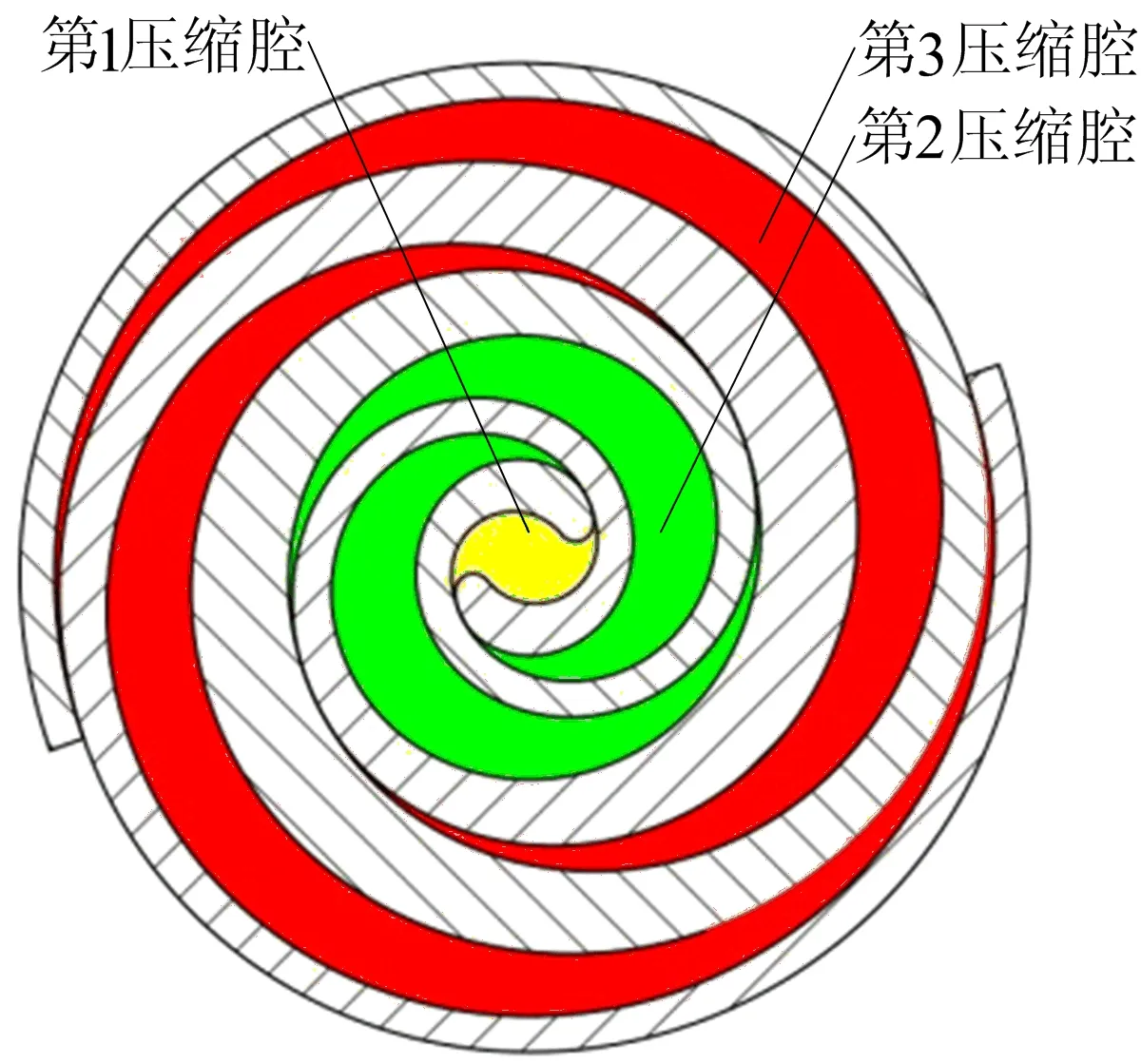
图4 涡旋压缩机腔体

2.1.1 第3压缩腔容积

当第3压缩腔由第2段和第3段圆渐开线组成时,第3压缩腔母线长度为:

(10)

第3压缩腔投影面积为:

A3(θ)=2Ror[L3+Rt(φe-2π)-Rt(φe)]

(11)

第3压缩腔容积为:

V3(θ)=hA3(θ)

(12)

其中:Ror为回转半径;h为涡旋盘齿高。

2.1.2 第2压缩腔容积

当第2压缩腔由第1段和第2段圆渐开线组成时,第2压缩腔母线长度为:

(13)

第2压缩腔投影面积为:

A2(θ)=2Ror[L2+Rt(φe-4π)-Rt(φe-2π)]

(14)

第2压缩腔容积为:

V2(θ)=hA2(θ)

(15)

2.1.3 第1压缩腔容积

1) 当第1压缩腔由第1段圆渐开线和修正圆弧组成时,第1压缩腔面积为:

(θ-π/2+δ)3+(φ+π+δ)3-

(φ+π-δ)3]-a2(π-4δ)-2Am

(16)

修正齿头轴向投影面积Am为:

(17)

第1压缩腔容积为:

V11(θ)=hA11(θ)

(18)

2) 当第1压缩腔完全由修正圆弧组成时,第1压缩腔面积为:

(19)

此时第1压缩腔容积为:

V12(θ)=hA12(θ)

(20)

其中:δ为渐开线发生角;γ为修正角;φ为修正展角;λ为圆弧中心角;Rd为大圆弧半径;Rx为小圆弧半径。

2.2 轴向气体力

涡旋压缩机涡旋盘上承受的轴向气体力是涡旋盘上承受的最重要的气体力,也是涡旋压缩机的一个主要缺点。动涡旋盘上承受的轴向气体力越大,动涡旋盘将沿轴向脱离静涡旋盘,增加涡旋盘之间的轴向间隙,导致压缩机径向气体泄漏量增加。因此,涡旋盘所受轴向气体力越小,对涡旋压缩机的力学性能越有利。

轴向气体力为:

(21)

其中,p1、p2、p3分别为第1、第2、第3压缩腔的压力,计算公式如下:

(22)

其中:ps为吸气压力;k为气体等熵指数。

2.3 压缩比

压缩比是衡量涡旋压缩机几何性能的一个重要指标,压缩比越大,涡旋压缩机容积效率越高。

压缩比为:

(23)

其中,θ*为开始排气角,θ*=1.5π-γ。

2.4 型线参数影响分析

由式(21)、式(23)可知,涡旋压缩机所受轴向气体力和压缩比都与连接点1处φ1、连接点2处φ2、修正底角β有关,下面利用控制变量法分别将各个型线参数对轴向气体力和压缩比的影响进行分析。

圆渐开线变截面涡旋压缩机第1段、第2段渐开线连接点1处φ1与压缩比v、轴向气体力Fa的关系如图5所示。

图5 φ1与压缩比、轴向气体力的关系

由图5可知,随着连接点1处φ1逐渐增大,圆渐开线变截面涡旋压缩机的压缩比和所受轴向气体力都逐渐减小,其中轴向气体力的减小速度小于压缩比的减小速度,说明φ1对轴向气体力的影响小于压缩比。因为压缩比的大小直接影响涡旋压缩机的几何性能,轴向气体力下降的同时,压缩比减小,不利于涡旋压缩机的几何性能,因此需要寻求两者的非劣解。

圆渐开线变截面涡旋压缩机第2段、第3段渐开线连接点2处φ2与压缩比v、轴向气体力Fa的关系如图6所示。

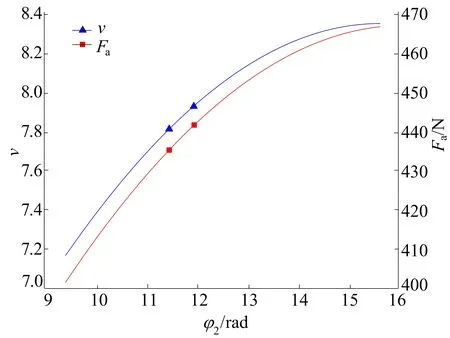
图6 φ2与压缩比和轴向气体力关系

由图6可知,随着连接点2处φ2逐渐增大,圆渐开线变截面涡旋压缩机的压缩比和所受轴向气体力都逐渐增大,其中轴向气体力的增加速度大于压缩比的增加速度,说明φ2对轴向气体力影响较大。因为轴向气体力的大小与涡旋压缩机的力学性能相关,所以轴向气体力越小,涡旋压缩机力学性能越好。但是压缩比增加的同时,轴向气体力也增加,涡旋压缩机的径向泄漏也增加,力学性能变差,因此需要寻求两者的非劣解。

修正底角β与压缩比和轴向气体力的关系如图7所示。

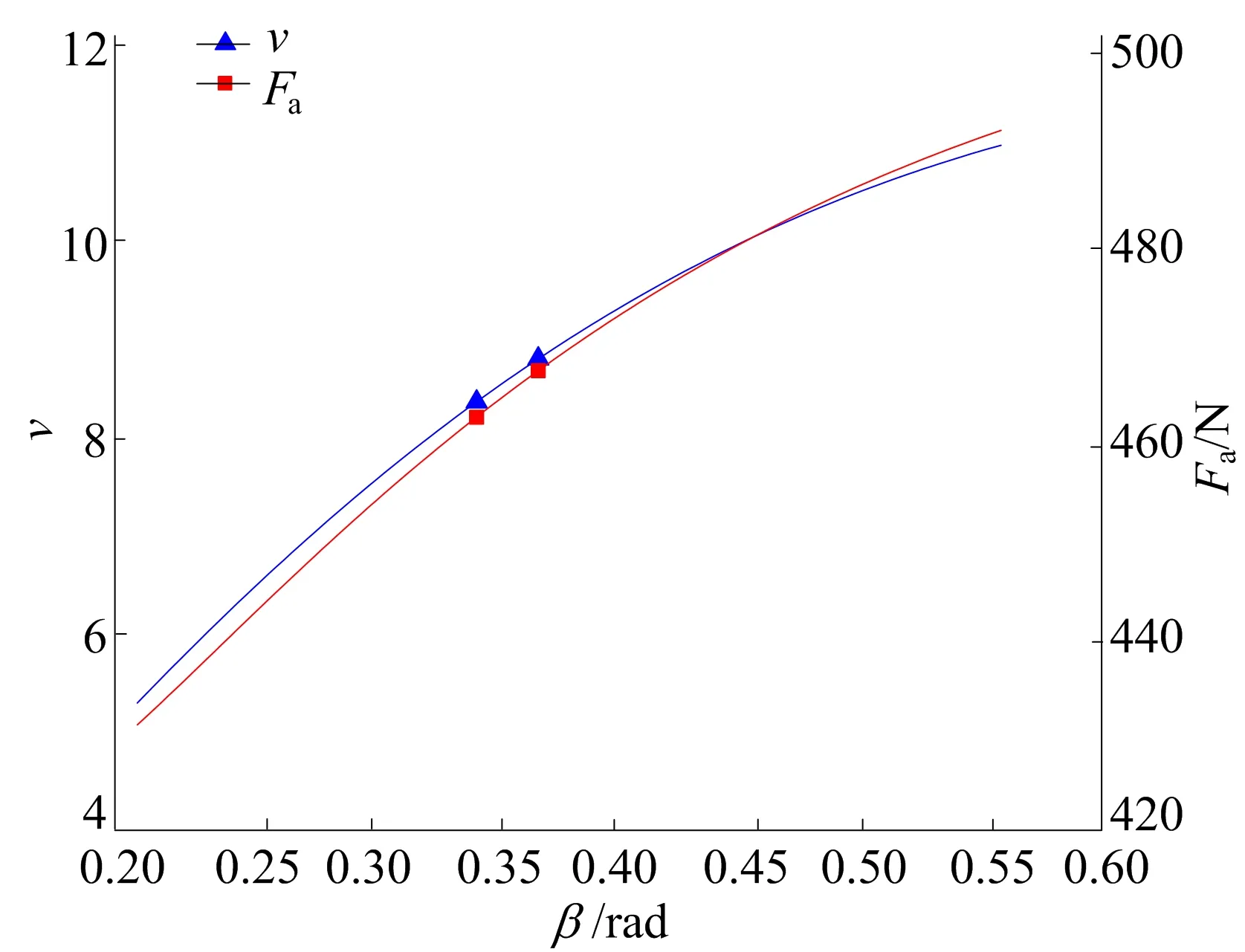
图7 β与压缩比和轴向气体力关系

与图5、图6对比可知,β对压缩比的影响明显大于φ1、φ2对压缩比的影响,对轴向气体力的影响小于φ1。

由图7可知,随着修正底角β的增大,圆渐开线变截面涡旋压缩机的压缩比和轴向气体力都逐渐增大,但是压缩比和轴向气体力的增速都逐渐减小,即随着修正底角的增大,对压缩比的影响和轴向气体力的影响逐渐减小。同样,压缩比增加的同时轴向气体力也增加,径向泄漏增加,对涡旋压缩机的力学性能不利,因此需要寻求两者的非劣解。

3 多目标遗传算法

3.1 多目标遗传算法

多目标遗传算法是利用仿生学中的选择、交叉、变异3个遗传算子,利用随机选择的父代对子代基因进行随机的交叉和变异,形成新的种群;并在新种群中利用适应度函数进行排序,选择出适应度较好的个体进行下一次迭代,直至得到最优解。

3.2 目标函数、优化变量和约束条件的选取

由图5、图6、图7可知,压缩比和轴向气体力在同一参数的区间变化上呈现相同的变化趋势,当其中一个目标性能变优的同时,另一个目标性能变差,因此需寻求两者的非劣解集。因为遗传算法优化默认的是最小值优化,所以目标函数选择为压缩比倒数(1/v)最小和θ=θ*时轴向气体力(Fa)最小。由于圆渐开线变截面涡旋压缩机的轴向气体力和压缩比有多个初始参数共同作用,因此在优化时,优化变量选择了相互独立的变量,即连接点1处φ1、连接点2处φ2和修正底角β。

综上,得到目标函数、优化变量和约束条件的关系如下:

(24)

3.3 单初始参数的优化

3.3.1 φ1、φ2的优化

由图5、图6可知,φ1、φ2都与轴向气体力和压缩比的性能好坏成相反的关系,因此利用多目标遗传算法对目标函数进行优化。分别对φ1、φ2利用多目标遗传算法进行优化,结果如图8、图9所示。

图8 优化连接点1处φ1

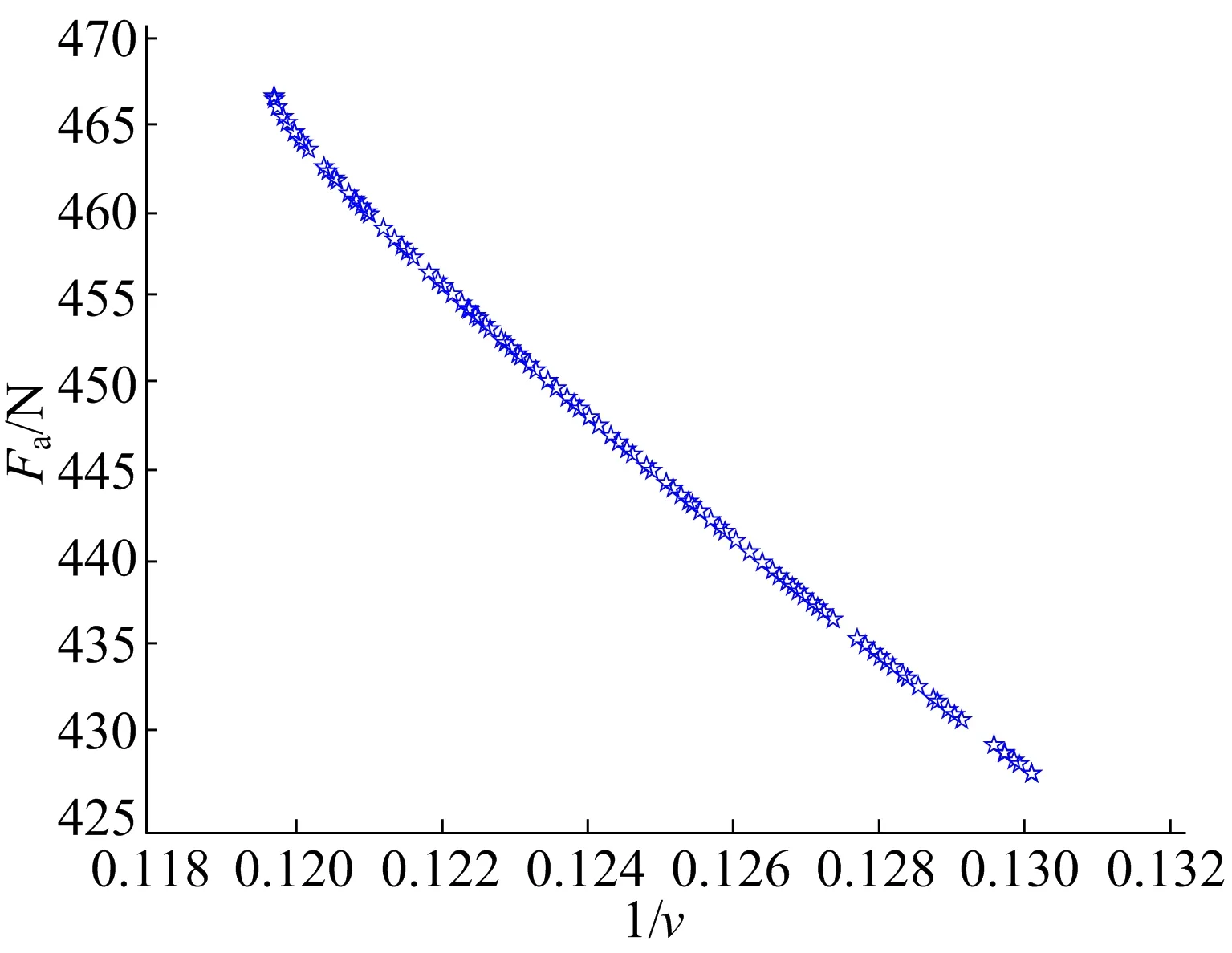
图9 优化连接点2处φ2

从图8、图9可以看出,随着φ1、φ2的变化,两目标函数呈现相反的变化趋势。

各自选取部分非劣解集见表1、表2所列。由表1、表2可知,随着连接点的变化,两优化目标的性能无法同时达到最优,而两表中φ1、φ2的取值则考虑了两优化目标性能的最优性。

表1 多目标优化下连接点1处φ1的非劣解集

表2 多目标优化下连接点2处φ2的非劣解集

3.3.2 β的优化

对修正底角β利用多目标遗传算法进行优化,结果如图10所示。

图10 优化β

从图10可以看出,随着β的变化,两目标函数呈现相反的变化趋势。与连接点处φ1、φ2的优化结果对比可知,修正底角β对压缩比的影响较大,对轴向气体力的影响较小。这同φ1、φ2、β与压缩比和轴向气体力的关系相对应,证明了优化结果的合理性。

选取部分非劣解集见表3所列。由表3可知,随着修正底角的变化,两优化目标的性能无法同时达到最优,而表3中β的取值则考虑了两优化目标性能的最优性。

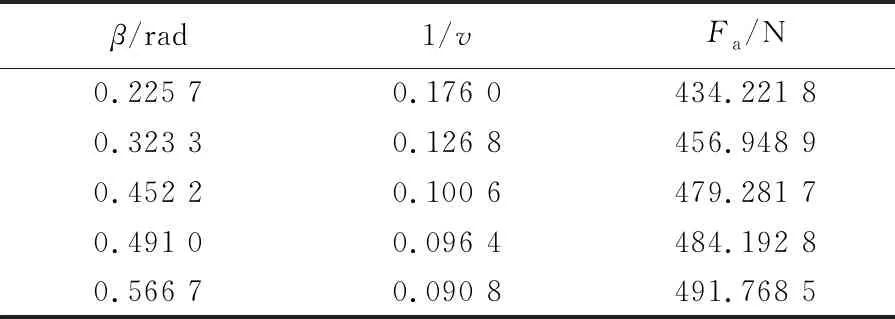
表3 多目标优化下β的非劣解集

3.4 多初始参数的优化

连接点处φ1、φ2和修正底角β同时变化时对两目标函数的取值进行优化,结果如图11所示。由图11可知,相对于单目标初始参数优化,多目标初始参数优化中轴向气体力和压缩比倒数的范围都更广,这为圆渐开线变截面涡旋压缩机设计时参数的取值提供了更大的选择空间。

图11 优化φ1、φ2和β

当φ1、φ2、β同时优化时,选取部分非劣解集见表4所列。

表4 多目标优化下φ1、φ2和β的非劣解集

由表4可知,两优化目标无法同时达到最优,而表4中φ1、φ2、β的取值则同时考虑了两优化目标性能的最优性。

3.5 优化前、后对比

在相同基圆半径和终端展角下,在多初始参数的非劣解集中选取一组优化型解集与未优化涡旋盘在压缩比和轴向气体力方面进行对比,结果见表5所列。

表5 多目标优化前、后涡旋盘参数对比

表5对比结果表明,经过多目标优化之后的优化型涡旋盘压缩比提升了16.14%,而轴向气体力减小了5.62%,有效改善了圆渐开线变截面涡旋盘的几何性能和力学性能。

4 结 论

本文以圆渐开线变截面涡旋压缩机为优化对象,分析得到连接点1处φ1与轴向气体力和压缩比负相关,连接点2处φ2、修正底角β都与轴向气体力和压缩比正相关;结合几何性能和力学性能对优化对象进行优化,利用多目标遗传算法分别在单初始参数和多初始参数条件下对目标函数进行优化,得到Fa和1/v的非劣解集;并得出在多初始参数优化下,目标函数的取值比单初始参数优化下范围更大;从定量角度将非劣解集中的优化型涡旋盘和未优化涡旋盘所受的轴向气体力和压缩比进行对比。结果表明,优化型涡旋盘在压缩比提升16.14%的同时,轴向气体力降低了5.62%,证明通过算法优化可以有效改善变截面涡旋盘的几何性能和力学性能。

因此,进行圆渐开线变截面涡旋压缩机设计时,可以根据相关性能的要求选取满足设计要求的型线参数,以得到兼顾几何性能和力学性能的圆渐开线变截面涡旋盘。