基于水动力分析的15 MW级半潜式漂浮基础优化研究

李 帅，任亚君，郝军刚，王富强，武明鑫，杨 阳

(1.水电水利规划设计总院，北京 100120；2.宁波大学海运学院，浙江 宁波 315211)

0 引 言

海上风电是可再生能源发展的重要方向，具备发展潜力大、离负荷中心近的优势。为实现“双碳”目标，十四五期间我国海上风电将进入规模化、商业化发展新阶段。深远海风能资源具有风速大、湍流强度小和发电利用小时数高、财务抗风险能力相对强等优点，考虑到资源潜力、生态影响及航运用海等因素，海上风电从近海走向深远海是必然发展趋势[1-2]，也是海上风电产业纵深发展的关键一环，同样是带动相关海洋产业协同发展的有效途径。

随着海上风电逐渐向深远海发展，传统的固定式基础难以满足经济性及安全性要求，漂浮式基础被证明适合深远海风电资源开发[3]。漂浮式基础可分为半潜式、驳船式、立柱式和张力腿等形式，其中半潜式基础具有适用水深范围广、稳性及耐波性好、建造运输方便、运行可靠、经济性相对较好等优点，是适合我国海况、具有巨大开发前景的基础形式。半潜式基础的研究相对较多，在较多示范项目中得到应用[4-6]，积累了较为丰富的工程经验。

虽然漂浮式风电技术得到一定发展，但我国目前工程技术成熟度较低、开发成本高，商业化规模应用仍面临较大挑战，我国也仅有三峡“引领号”、海装“扶摇号”、中海油“观澜号”等示范性工程。浮式基础单位兆瓦用钢量是浮式基础先进性的技术指标之一，也是影响漂浮式海上风电项目开发投资的重要因素。“引领号”三立柱半潜式浮式基础总用钢量5 500 t左右，单位用钢量1 000 t/MW；“扶摇号”三立柱浮式基础总用钢量3 900 t左右，单位用钢量为630 t/MW；“观澜号”四立柱浮式基础总用钢量4 000 t左右，单位用钢量555 t/MW。距离科技部重点专项中提出的500 t/MW考核指标还有差距。

一些学者指出，可以通过设计新的浮式基础形式[7]、使用混凝土材料[8-9]等方法降低用钢量及建造成本，典型研究成果包括由X1 Wind公司设计的PivotBuoy浮式风电基础、法国公司Eolink研发的浮式风电设计Eolink方案、丹麦的Tetraspar、Braceless半潜浮式以及双机头基础等。国内也有很多针对新基础形式的研究成果，丁红岩等[9]提出一种新型张紧式系泊系统的全潜式浮式风机基础，并采用FAST软件耦合水动力-空气动力-控制系统-系泊系统对不同风况下的浮式风机及全潜式浮式基础的动力特性进行分析；张浩等[10]结合半潜式和单立柱式海上风机浮式基础的特点，提出了一种用于海上风机的新型钢格构式基础，其纵摇、横摇及艏摇响应更小，具有更好的稳定性；Lai等[11]设计了一种适合我国海况的带有阻尼结构的深吃水半潜式平台，通过数值方法研究其水动力性能；蔡新等[12]基于初稳性设计原理并借鉴半潜式与单柱式浮式平台的结构特点，设计了一种大吃水、小水线面面积、具有倾斜侧柱的新型浮式平台，该新型浮式平台能够明显优化水动力系数，在受到外部载荷后具有较好的恢复能力；杜宇等[13]针对半潜漂浮式风电基础初步选型，采用Pareto-Optimal评价方法对不同吃水、平台立柱直径、立柱间距和垂荡板直径四个参数的不同组合进行了分析比较，力争确定最优的尺寸组合。

但以上研究多针对5～10 MW的风电机组，为进一步降低浮式基础单位兆瓦相关成本，使用大容量机组是实现浮式风电规模化商业开发的有效手段。平台优化设计不仅需要考虑浮式基础的经济性特征，还需要保证足够的稳定性与安全性。对15 MW大型风机而言，浮式基础的动力性能直接关系到漂浮式海上风机系统的运行安全。因此，需针对15 MW级漂浮式海上风机开展海洋环境荷载作用下的动力响应研究，优化基础平台设计方案，从而提高大型漂浮式风机系统稳定性、可靠性、安全性和经济性。

考虑到我国漂浮式海上风电尚处于起步阶段，本文以采用传统钢结构三立柱半潜式浮式基础形式(平台I)为研究对象，并通过减小边柱尺寸方式对浮式基础进行优化(平台II)，从而减小用钢量。采用ANSYS/AQWA建立数值计算分析模型，针对15 MW级三立柱半潜浮式基础平台开展水动力性能、动力响应及锚泊系统性能研究，并通过计算对比优化前后2种平台的附加质量、辐射阻尼、一阶波浪力以及波浪作用下的平台运动特性和系泊系统动力特性，评估分析优化方向的合理性及有效性。

1 浮式风电平台水动力分析基础理论

1.1 浮体运动控制方程

半潜漂浮式风机系统主要由发电机组系统、浮式基础系统和系泊系统等组成。整体系统的运动学方程可以表示为

(1)

式中，Mij为漂浮式风机系统的质量矩阵；Fplatform为浮式平台所受水动力载荷及系泊系统载荷；Fwind为风荷载。

浮式平台荷载Fi，platform可以表示为

Fi，platform=-Aijxi+Fi，hydro+Fi，lines

(2)

式中，Aij为附加质量矩阵；Fi，hydro为水动力荷载，包含静水恢复力、辐射阻尼力、浮力、粘性阻尼力和波浪力等；Fi，lines为锚链荷载。

1.2 势流理论

水动力荷载Fi，hydro可表示为以下形式

Fi，hydro=Fi，waves+ρgV0δi3-Cij，hydrostaticxi-

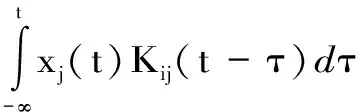
(3)

式中，Kij为辐射阻尼迟滞函数；Cij为静水恢复力矩阵；Fwaves为波浪荷载，即入射波对平台总激励力荷载。上述参数均可通过势流理论求解。

2 浮式基础模型参数

2.1 2种半潜浮式风机平台参数

本文对三立柱半潜漂浮式风机平台的相关水动力特性进行分析研究，平台设计基于美国可再生能源实验室(NREL)的OC4三立柱形式，并通过相关简化而成(平台I)：①取消撑杆并对垂荡板进行优化，可在一定程度上减小撑杆引起的疲劳荷载，并减小平台运动响应；②取消中柱并将风机放置在其中一根边立柱上。“扶摇号”、“引领号”等均采用此形式，利用浮心与重心间距产生与风倾力矩相反的回复力矩，可有效降低风倾力矩的作用，提升平台稳定性。

观察结构形式可知，当主柱上加载风机塔筒时，为了保持荷载平衡，需要在另外两个边柱上施加同样荷载的压载水，以平衡同等尺寸边柱提供的浮力。从受力角度而言，边柱提供的浮力只需要同自身重力与压载水重力之和相等即可，无需提供和主柱重力同等的浮力(即无需提供与风机同等质量压载水的浮力)，即可以降低边柱尺寸从而降低边柱提供的浮力。因此，为减少用钢量，提高经济性，在平台I的基础上，保持主柱直径不变，减小两个边柱直径，从而减小提供的浮力及压载水质量，同时保持系统平衡，形成平台II。

在同等壁厚情况下，相比于平台I，平台II可节约用钢量5.85%(约400 t)，两种半潜式平台示意见图1，平台的主要参数如表1所示。

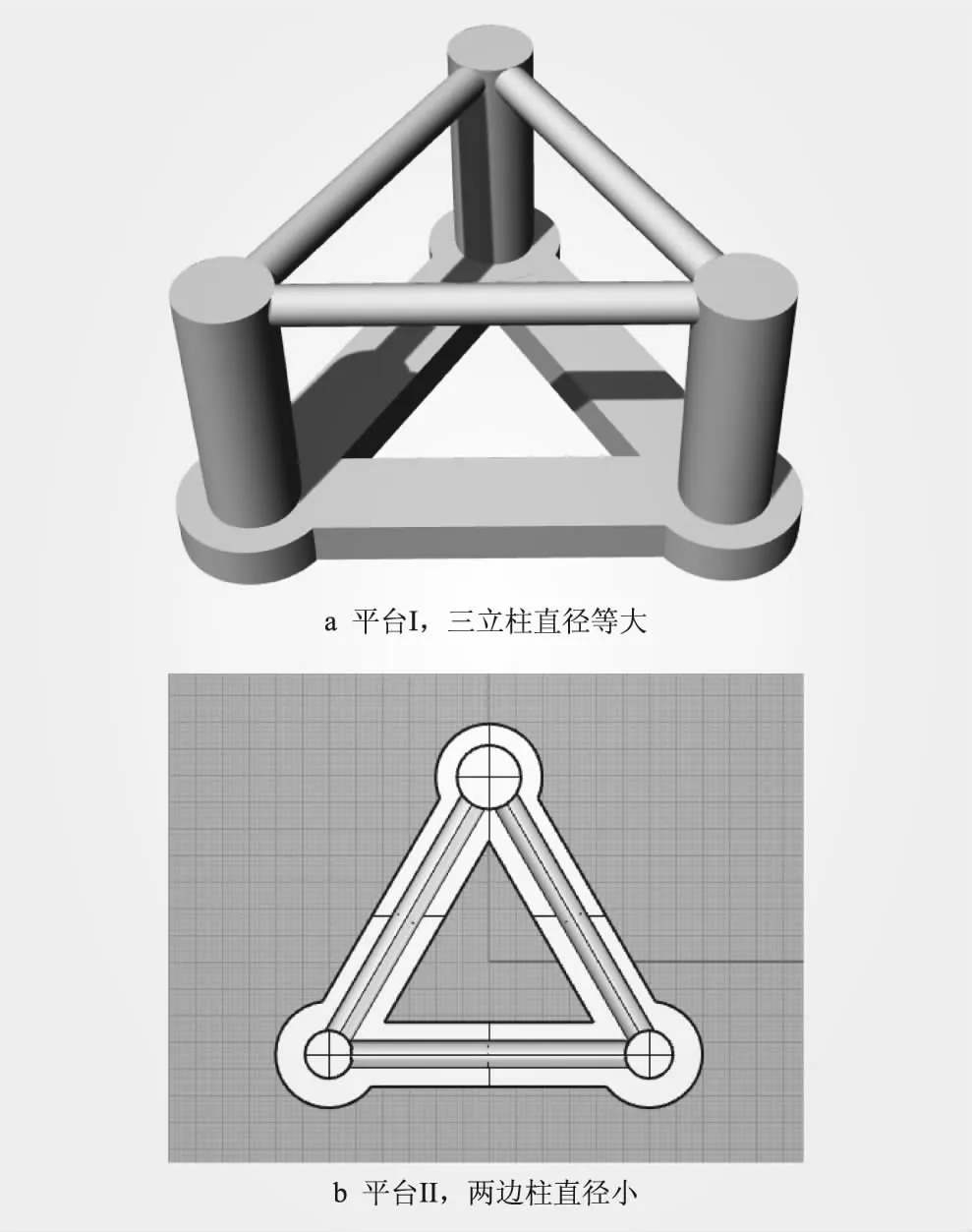
图1 半潜式浮式平台示意

表1 平台I和平台II相关信息

2.2 系泊系统参数

2个半潜浮式风机平台锚泊系统均由3根锚链组成，每两条锚链之间的夹角为120°，适用于100 m水深海域。锚泊系统布置示意见图2，其中波浪方向沿X轴正方向，锚链的相关参数见表2。

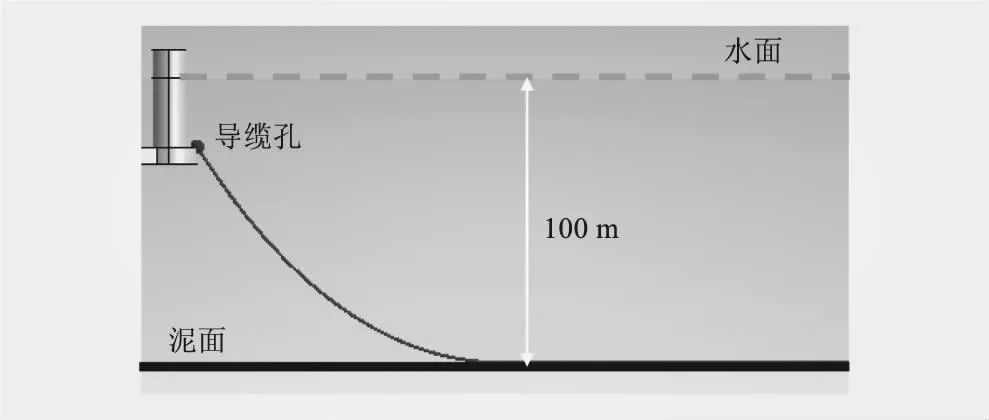
图2 系泊系统示意

表2 系泊系统相关参数

3 水动力分析成果

3.1 频域水动力分析

3.1.1 附加质量与辐射阻尼

浮体在自身运动时会产生附加质量与辐射阻尼。

图3为在ANSYS/AQWA中通过势流理论计算得到的2个半潜浮式风机基础(平台I和平台II)的附加质量(纵荡、垂荡、纵摇)。从图3可以看出，两个浮式基础的附加质量变化趋势基本一致；纵摇方向的附加质量大于纵荡和垂荡方向；纵荡和垂荡方向附加质量在高频区变化较小，逐渐趋于稳定。相比于平台I，平台II在纵荡、垂荡、纵摇方向的附加质量(最大值)分别减小23.5%、增加3.45%、增加4.89%。

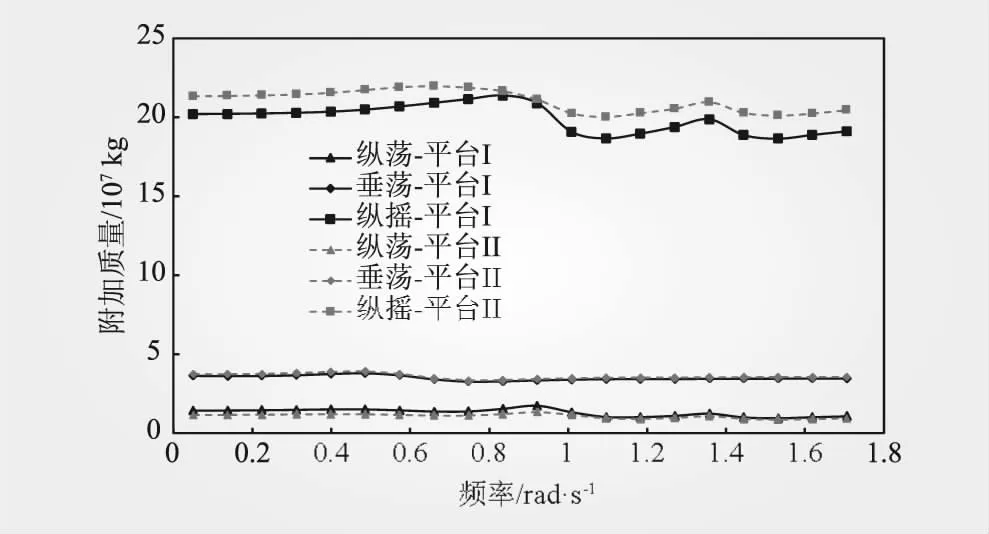
图3 两浮式平台附加质量曲线

3个方向的辐射阻尼如图4所示，纵摇方向辐射阻尼整体上大于纵荡和垂荡方向。纵摇和纵荡方向辐射阻尼在高频区较大且有2个峰值，分别出现在1 rad/s和1.42 rad/s；垂荡方向辐射阻尼最大值出现在0.6 rad/s；平台II与平台I的辐射阻尼变化趋势基本一致，纵摇和纵荡方向最大值分别降低36%、57%，垂荡方向变化较小。

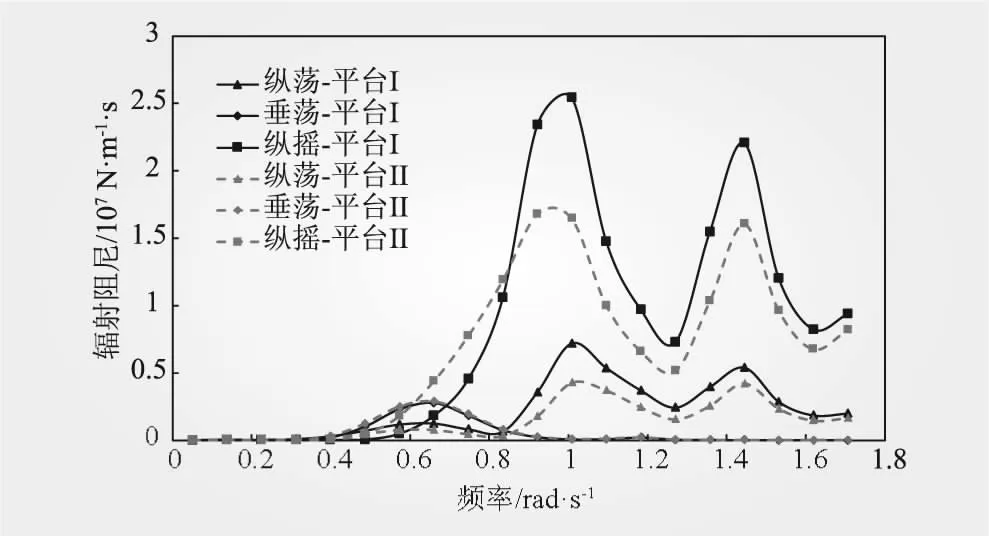
图4 两浮式平台辐射阻尼曲线

3.1.2 一阶波浪激励力

根据波浪理论，一阶波浪激励力即佛汝德-克雷洛夫力和绕射力的合力。本文两平台均关于X-Z平面对称，故仅考察0°、45°、90°入射波浪角时平台产生的一阶波浪力曲线。纵荡、垂荡、纵摇方向的一阶波浪力传递函数如图5所示。

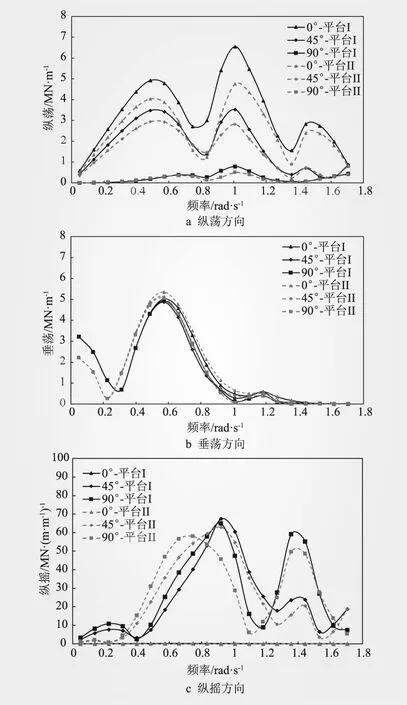
图5 两浮式平台一阶波浪力传递函数曲线

从图5a可以看出，纵荡方向一阶波浪力具有多个峰值，且各个入射方向的波浪力变化趋势基本一致；入射角为0°时一阶波浪力大于45°和90°；考虑到平台关于X轴对称，当入射角为90°时，平台所受波浪力较小。相对于平台I，平台II在0°、45°和90°入射角时所受波浪力分别降低29.3%、21.2%和36.8%。

从图5b可以看出，平台II和平台I所受波浪力的规律一致，最大值均出现在0.57 rad/s；此外，各个入射角度的一阶波浪力曲线基本一致，说明波浪入射方向对垂荡方向的一阶波浪力影响较小。两个平台所受波浪力在数值上差异较小，但低频区平台II所受波浪力小于平台I。

从图5c可以看出，0°方向的一阶波浪力较小；当入射角为45°和90°时，纵摇方向一阶波浪力具有多个峰值，且各个入射方向的波浪力变化趋势基本一致。当频率小于0.8 rad/s时，平台II一阶波浪力大于平台I，当频率大于0.8 rad/s时，平台II一阶波浪力小于平台I；相比于平台I，45°和90°的一阶波浪力极值差异分别为-11.0%、-5.43%。

3.1.3 幅值响应算子

幅值响应算子(RAO)为浮式风机平台运动幅值与波幅之比，表征浮式平台抵抗波浪荷载的能力。入射角0°、45°、90°的波浪作用于两浮式平台上时，纵荡、垂荡及纵摇方向的RAO如图6所示。

图6 两浮式平台幅值响应算子

从图6a可以看出，两平台纵荡方向的RAO数值及变化趋势基本一致，随着频率的增加逐渐下降，并逐渐趋近于0；由于两平台均关于Z-X平面对称，当入射角为90°时，纵荡方向的RAO较小。

从图6b可以看出，在频率小于0.4 rad/s时，平台II和平台I垂荡方向RAO曲线差异较大，平台I和平台II最大值分别出现在0.224 rad/s和0.312 rad/s；当频率大于0.4 rad/s时，两平台RAO变化趋势相同，随着频率增加逐渐减小并趋近于0；平台I受入射角度影响较小，变化趋势相同且数值上差异较小；平台II的RAO变化趋势受入射角影响较小，数值上受入射角影响较大。

从图6c可以看出，不同入射方向对纵摇RAO曲线有一定影响，当入射角为0°时，两平台RAO值均较小；当入射角为90°时，平台I和平台II的RAO峰值分别出现在频率为0.224 rad/s和0.573 rad/s；当波浪频率大于0.3 rad/s时，平台II的RAO大于平台I。

3.2 固有周期

为研究2个半潜浮式基础各运动方向固有周期，开展了平台在无风浪流荷载作用、给定初始位移或转角工况下，6个自由度方向上的自由衰减运动模拟。纵荡方向5 000 s的自由衰减时程曲线如图7所示，从图7可以看出，平台II纵荡方向周期略小于平台I；将自由衰减时程曲线转换为功率谱密度曲线(见图8)，功率谱密度峰值频率即为浮式基础在对应自由度方向上的固有频率(见表3)。从表3可以看出，平台II在纵荡、横荡、首摇方向周期小于平台I，而垂荡、纵摇、横摇方向周期大于平台I；整体而言，两平台固有周期满足均满足DNV规范要求[14-15](纵荡大于100 s，垂荡为15～25 s，纵摇为25～40 s)。

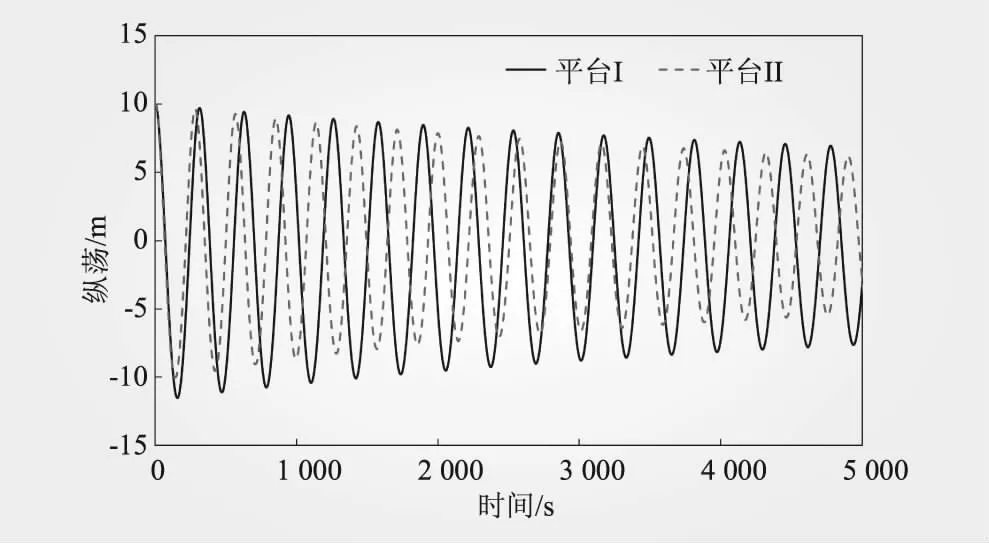
图7 两浮式平台纵荡方向自由衰减振动曲线

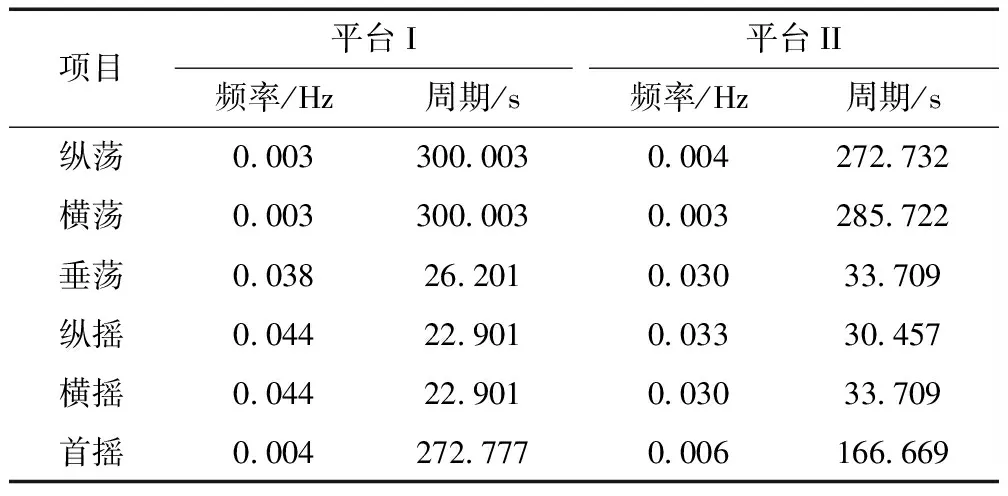
表3 两浮式平台固有周期统计

3.3 运动特性分析

针对2个半潜浮式风机平台进行海浪作用下的时域仿真模拟。结合海南某项目工程海域实测海况数据，结合15 MW风机系统工作环境要求，100 m水深极端工况下有义波高为11 m，谱峰周期12.1 s。波浪方向为0°，波浪谱选用JONSWAP谱，谱峰因子为3.3；波模拟时长为6 000 s。为消除瞬态效应，在时域及频域数据处理时均去掉前1 000 s的数据。

图9为两浮式基础在相应海况下纵荡、垂荡以及纵摇方向的时域运动响应。从图9可以看出，平台II和平台I在纵荡、垂荡方向的运动趋势基本一致，纵摇方向运动有一定差异，时域运动响应的特征指标统计值如表4所示。从表4可以看出，两平台在纵荡方向上的运动幅度差异较小，约0.21%，但是平台I在正向、负向运动差异较大；平台II垂荡方向运动幅度增加22.22%，两平台纵摇方向运动幅度均较小，且平台II减小72.54%。

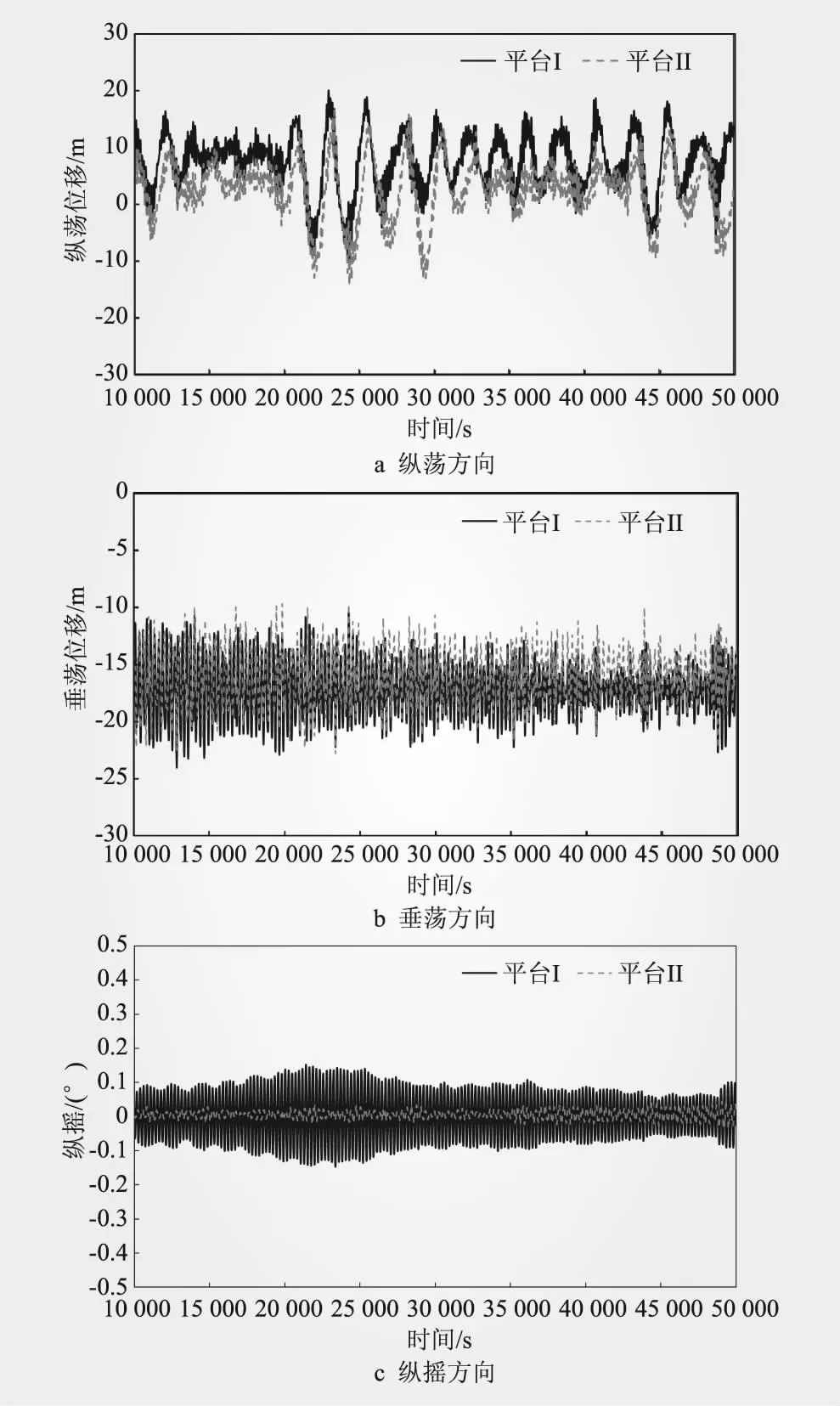
图9 两平台纵荡、垂荡以及纵摇方向的时域运动响应

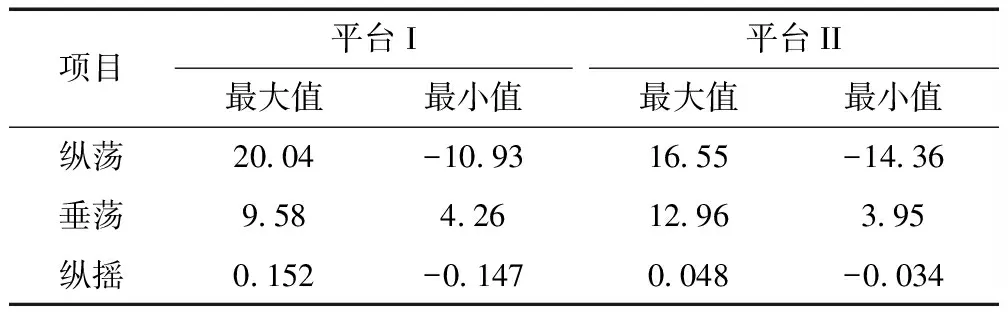
表4 两平台纵荡、垂荡、纵摇方向运动特征统计 m

图10为两平台相应海况纵荡、垂荡以及纵摇3个方向上平台运动的功率谱密度(PSD)曲线。从图10可以看出，纵荡方向幅值大于垂荡及纵摇方向，且纵荡、垂荡方向有2个峰值，纵摇方向有3个峰值。纵荡方向两平台峰值均为0.003 255 2 Hz和0.075 Hz，其中前者为纵荡方向固有频率，后者为波浪频率；垂荡方向，平台I的峰值频率分别为0.039 1 Hz(垂荡方向固有频率)、0.075 Hz(波浪频率)，平台II为0.029 3 Hz(垂荡方向固有频率)及0.075 Hz(波浪频率)；纵摇方向，平台I峰值频率为0.003 255 2 Hz(纵荡方向固有频率)、0.042 3 Hz(纵摇固有频率)，平台II峰值频率为0.003 255 2 Hz(纵荡方向固有频率)、0.032 6 Hz(纵摇固有频率)和0.075 Hz(波浪频率)。从图10还可以看出，平台固有频率处的峰值大于波浪频率处峰值，且平台I的波频响应明显大于平台II。

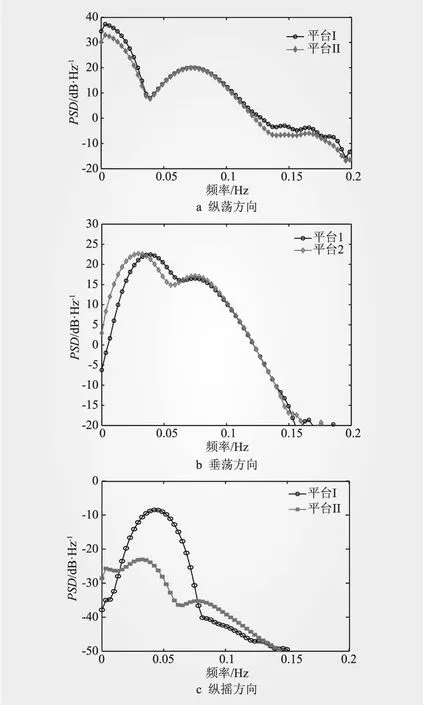
图10 两平台纵荡、垂荡以及纵摇方向的时域运动响应的功率谱曲线

3.4 系泊系统分析

漂浮式海上风电锚泊系统能够维持风机系统的稳定，限制风机平台的运动响应，保持风机正常工作，保证机组的发电效率。因此，研究锚泊系统的动力响应具有重要意义。本文旨在研究在两种浮式基础在相同海况下锚泊系统的动力响应，包括锚链张力、卧链长度及上拔力等。

3.4.1 锚链张力

锚泊系统张力荷载动力响应曲线如图11所示。从图11可以看出，两平台的系泊系统受力曲线变化规律基本一致，1号锚链受力大于2号锚链和3号锚链。相比于平台I的1 137 kN的1号锚链受力，受力为805.8 kN的平台II受力减小29.15%；由于对称性、入射角为0°，2号锚链和3号锚链受力基本一致，平台II受力峰值为316.8 kN，相比于平台I的289.4 kN，增加9.47%。

图11 两平台系泊锚链张力时程曲线

两平台的锚泊张力功率谱密度曲线如图12所示。从图12可以看出：平台II和平台I变化趋势相同，峰值频率均为0.003 25 Hz和0.075 Hz，说明锚链受力主要是由纵荡频率和波浪频率确定，这对于后期锚泊系统设计具有一定的指导意义。

图12 两平台的锚泊系统张力功率谱密度曲线

3.4.2 卧链长度

虽然卧链长度通常不作为评估系泊系统动力性能的指标，但考虑到优化系泊系统的需要，也将该指标进行对比。锚泊系统卧链长度动力响应曲线如图13所示。从图13可以看出，两平台的系泊系统卧链长度曲线变化规律基本一致，且1号锚链变化范围大于2号锚链和3号锚链。平台I的1号锚链卧链长度最小值为48.08 m，平台II为111.04 m；由于对称性，2号锚链和3号锚链的卧链长度及变化趋势基本一致，平台II的卧链长度为232.96 m，相比于平台I的250.30 m，减小6.93%。

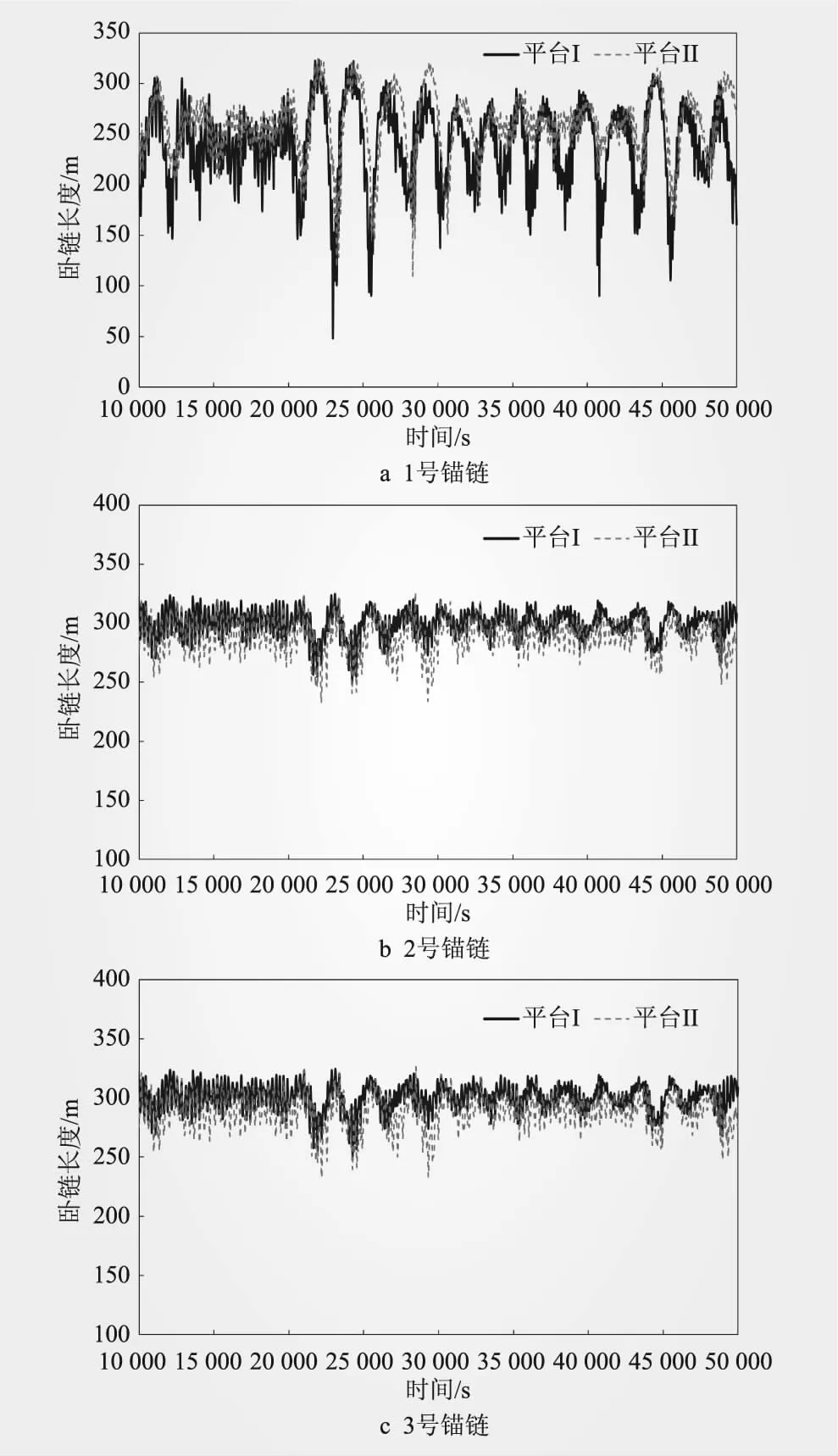
图13 锚泊系统卧链长度动力响应时程曲线

3.4.3 锚上拔力

锚泊系统锚固点承受的上拔力曲线如图14所示。从图14可以看出，两平台的系泊系统上拔力曲线在大部分时间趋近于0，仅1号锚链受力在个别时刻较大，2号锚链和3号锚链的受力均较小。平台I的1号锚链上拔力最大值为6 094.38 N，平台II为224.68 N，是平台I的3.69%；由于对称性，两平台的2号锚链和3号锚链上拔力变化趋势及数值基本一致，虽然平台II大于平台I，但数值上均较小，说明目前设计的系泊系统是合理的、安全的。

图14 锚泊系统锚固点承受的上拔力曲线

4 结 论

本文以三立柱半潜漂浮式基础平台(平台I)为研究对象，通过减小偏柱尺寸方式对其进行优化设计(平台II)，从而减小用钢量。采用ANSYS/AQWA建立两个浮式基础的水动力数值分析模型，并开展系统的水动力性能对比分析研究，得到如下结论：

(1)两平台的附加质量、辐射阻尼、一阶波浪力曲线变化规律相似；相比于平台I，平台II在纵荡、垂荡、纵摇方向的附加质量减小23.5%、增加3.45%、增加4.89%；纵摇和纵荡方向辐射阻尼最大值分别降低36%、57%，垂荡方向变化较小；平台II纵荡方向在0°、45°和90°入射角时所受波浪力分别降低29.3%、21.2%和36.8%，纵摇方向入射角为45°和90°的一阶波浪力极值差异分别为-11.0%、-5.43%。

(2)两平台固有周期有一定差异。相比于平台I，平台II在纵荡、横荡、首摇方向固有周期减小9.09%、4.76%、38.90%，在垂荡、纵摇、横摇方向固有周期增加28.65、32.99%、47.19%。平台II的固有周期均满足规范要求。

(3)两平台在相应海况下运动特性规律基本一致，相比于平台I，平台II纵荡方向上的运动幅度减小0.21%，垂荡方向运动幅度增加22.22%；两平台纵摇方向运动幅度均较小，相比而言，平台II较平台I减小72.54%。

(4)两平台的系泊系统受力曲线变化规律基本一致，且1号锚链受力大于2号锚链和3号锚链。相比于平台I，平台II的1号锚链受力减小29.15%，2号锚链和3号锚链增加9.47%，但整体数值小。

综上所述，本文中的两个浮式基础平台水动力性能较好，运动特征、系泊系统响应等特性合理，优化后的浮式基础水动力性能基本与优化前一致，用钢量减小5.85%(约400 t)，说明提出的优化方向是可靠、可行的，为降低三立柱半潜式基础平台用钢量提供了一种新思路，新方向。

值得说明的是，本文仅从水动力特性方面对平台优化进行了验证分析，后续还需针对整个浮式风机系统开展气动-伺服-水动-弹性全耦合一体化数值仿真，进一步验证优化的可行性、合理性。