卡尔曼滤波法在大跨度波形钢腹板刚构桥施工变形控制中应用研究

杨勃 陈艳茹 张鹏

摘 要： 大跨度连续钢腹板刚构桥悬臂施工中，由于跨度大控制不准确，容易造成线性偏离设计要求，或者合攏困难等工程问题。所以在施工过程中，对桥梁施工的线性进行控制进行十分必要的深入研究，结合XX连续T型钢腹板刚构桥的悬臂施工监控量测方案，采用卡尔曼滤波法来分析连续T型钢腹板刚构桥悬臂施工线性控制中误差的分析，通过数据分析和详细的演算并结合工程实际来验证施工控制误差调整的常用方法和原理，同时也为类型工程施工控制提供有效的借鉴经验。

关键词： T型刚构；线性控制；钢腹板；卡尔曼滤波法

中图分类号： TQ050.4+1

文献标志码： A  文章编号： 1001-5922（2023）08-0166-05

Application research of kalman’s filtering method on deformation control of rigid frame bridge with long span corrugated steel web

YANG Bo1，CHEN Yanru1，ZHANG Peng2

（1.Shaanxi Institute of Railway Engineering Technology，Weinan 714000，Shaanxi China；

2.China Rail Way First Survey and Designin Stitute Group Co.，Ltd.，Xi’an 710043，China）

Abstract： Due to the large span and inaccurate control of Long-span continuous rigid frame bridge in cantilever construction，it is prone to cause the linear deviate from the design requirements，and engineering problems like folding difficulty.So in large span continuous rigid frame bridge construction process，it’s necessary to perform in-depth research of the linear of bridge construction control.Combined with the cantilever construction monitoring and measurement scheme of continuous steel web rigid frame bridge，the Kalman filter method was used to analyze the error analysis in the linear control of continuous steel web rigid frame bridge construction，and the common methods and principles of construction control error adjustment were verified through data analysis and detailed calculation combined with the engineering practice，which also provided effective reference experience for the construction control of type engineering.

Key words： T rigid frame；linear control； cantilever construction； kalman’s filtering method

卡尔曼滤波法参数估计法很容易推广到非线性系统中去，成为推广的卡尔曼参数估计法。预应力混凝土刚构桥随着跨径逐渐的增大，采用分段施工后，为了满足成桥线形要求必须对施工过程进行有效控制，在施工控制中，根据计算条件模拟施工过程准确计算每个施工阶段的预拱度，采用科学方法对施工过程各种误差进行纠偏和调整。 预拱度的计算可以按照施工顺序采用结构计算软件分析获得，然而对于施工误差的控制，测量，评价，调整也很重要，桥梁结构的力学和变形数据状态基本是采用离散的数据序列表示（例如：标高、应力等），所以我们在施工控制中使用的是离散线性数据量系统的卡尔曼滤波法[1]。尤其对于钢腹板刚构桥梁的施工控制研究，大气温度、焊接温度对于钢腹板变形影响比较大。

1 建立Kalman滤波模型

1.1 原理

在忽略控制力条件状况下，系统的状态方程以及观测方程调整为：

[JB（{]x k+1=G k+1x k+w k

Z k=C kx k+v k  （1）

式中：

w k — n 维状态向量；

G K+1—n×n 状态转移矩阵；

w k—p  维随机干扰向量；

z k — m 维观测向量；

C K — m×n 观测矩阵；

v k — m 维观测噪声向量。

假设初始状态 x 0 的统计特性为

E（x 0）=m 0

E （x 0－m 0）（x 0－m 0）T =P 0

且 x 0与 w k 、 v k 均互不相关，即

E （x 0－m 0）wT k =0

E （x 0－m 0）vT k =0

现在用递进推演的方式来表达出每个时间点 k 在取得的观测数据的基础上所做出的状态 x k 的估计 x  ^  k 。这样，在 x  ^  0 ＝ m 0 的基础上，逐次令 k= 1，2，…就能用递推公式求出各个时刻的估计值 x  ^  1 ， x  ^  2 ，…。

基本离散线性系统

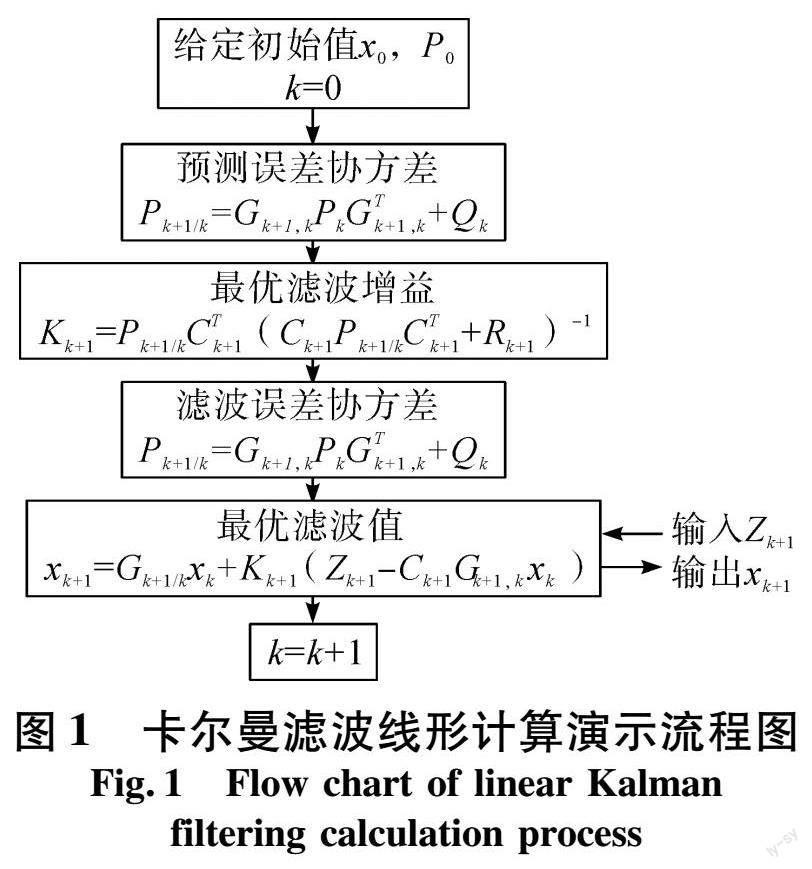
主要适用于可调变量极少的大跨径桥梁结构中，所以它很适合于悬臂施工的大跨径预应力混凝土连续刚构桥。具体的关系曼滤波线形计算演示流程如图1所示。

当结构某一节段施工完成后，无论结构参数处于什么样的状态（比如标高），我们基本上没有办法来改变本施工阶段的结构标高。我们所能做的是：根据本阶段的标高误差来预测或估计出下一节段的立模标高，使随后的结构实际状态符合结构的设计理想状态，这就是基本离散线性系统卡尔曼滤波的实际意义。

1.2 建立状态方程

对于悬臂施工的大跨径预应力混凝土鋼腹板连续T型刚构桥而言，可以把钢腹板连续T型刚构桥对称的大小里程方向的预留拱度值作为状态变量，对于已经施工阶段 k 及准备下一段施工阶段 k+1 ，则有状态方程：

x k+1=G k＋1x kw k

（2）

式中： G k+1 为 k+1 阶段与 k 阶段悬臂段预留拱度计算值之比，即

G k+1=x k＋1/x k

（3）

因为已经浇筑梁段的预留拱度值可以现场观测，所以才有下列观测方程：

Z k=X k＋v k

（4）

1.3 滤波方程的解

比较式（1）及式（4），可知 C k=I （单位矩阵），所以卡尔曼滤波求解递推公式则演变为：

1）滤波算法

X  ^  k+1=X  ^  k＋1/k＋K k+1（Z k+1－X  ^  k）   （5）

2）预测算法

X  ^  k+1/k=G k＋1，kX k   （6）

3）滤波增益

K k+1=P k+1/k（C k+1P k+1/kCT k+1+R k+1）－1

（7）

4）滤波误差协方差

P k+1=（I-K k+1C k+1）P k+1/k

（8）

5）预测误差协方差

P k+1/k=G k+1，kP kGT k+1，k+Q k

（9）

1.4 初始条件和误差参数的确定

预应力混凝土钢腹板连续T型刚构桥如果采用悬臂施工方法，计算预留的预拱度值和预留拱度差值的平方取为：

x（0/0）=x 0=0# 块左右两端理论计算预留拱度值， P（0/0）=P 0=0# 块左右两端理论计算预留拱度值与实测预留拱度值差值的平方[2]。为了得到各个阶段的预测值与滤波值，还需定义 R k+1 及 Q k ：

R k+1=   σ L（k+1）2  00  σ R（k+1）2

（10）

式中： σ L（k+1） ＝小里程悬臂端 k+1 阶段预拱度的测量误差的均方差；

σ R（k+1） ＝大里程悬臂端 k+1 阶段预拱度的测量误差的均方差6；

σ L（k+1） 、 σ R（k+1） 与测量仪器的性能及悬臂长度有关。

Q k=   σ 1/L（k）2  00  σ 1/R（k）2

式中： σ 1/L（k） ＝小里程悬臂端 k 阶段计算误差的均方差；

σ 1/R（k） ＝大里程悬臂端 k 阶段计算误差的均方差；

σ 1/L（k） 、 σ 1/R（k） 表示计算误差的范围，难以准确确定，可假定为悬臂长度的线性函数或二次幂函数。

P 0，0 =P 0=0 块大小里程两端理论计算预留拱度差值的平方。在实际悬臂施工应用过程中，可将悬臂端阶段末预留拱度定义为状态向量 x ，立模时的预留拱度可通过阶段末的预留拱度加上相应阶段的挠度计算值获得3，若将 k 阶段预测 k+1 阶段立模时的预留拱度值记为 X0 k+1，k ，将 k+1 阶段的端点挠度计算值记为 d k+1 ，则有

x0 k+1，k = x  ^  k+1，k + d k+1

（11）

对于系统误差，可以通过悬臂端各节段的预留拱度滤波值 x  ^  与理论计算值 x 的趋势比较分析确定，若滤波误差 x′＝x-x  ^  带有明显的方向性如图2的（a）、（b）、（c）、（d），则 x′ 为系统误差；若 x′ 无明显的方向性如图3的（e）、（f），则 x′ 不是系统误差，即系统误差不明显，可忽略不计[3]。

若存在系统误差，则当前阶段（已完成阶段）的系统误差为：

x′  k=x k-x  ^  k

下一阶段（待施工阶段）的系统误差预测值为：

x′ k+1=x k+1-x  ^  k+1，k

如果不存在系统误差，则参数与预留拱度不需要进行修正和调整，则可直接采用预测值 x  ^  k+1，k 下一阶段的预留拱度值[4]。如果系统误差存在，则参数和预留拱度调整需要进行[5]。按照参数调整后，对下一阶段预留拱度由原定理想状态到随后理想状态的改变量 δ k+1 与系统误差预测值 x′ k+1 的关系可分为以下两种情况来确定调整量（ δT k+1 ）[6]：

δT k+1 确定以后，将其加入下式的右端项，可以得到下一阶段立模时的预留拱度值[7]：

所以滤波误差计算的几种情况[8]如图2所示。

x0 k+1/k = x  ^  k+1/k + d k+1 + δT k+1

1.5 各施工阶段完成后预留标高的确定

各个梁段预设标高为： H a k =H s k +x k ；式中 H a k  为 k 节点施工立模板标高值， H s k  为 k 节段观测点的设计标高值； x k 为 k 节段施工抛高值[9]。

2 Kalman滤波法在施工控制中的应用

2.1 工程概况

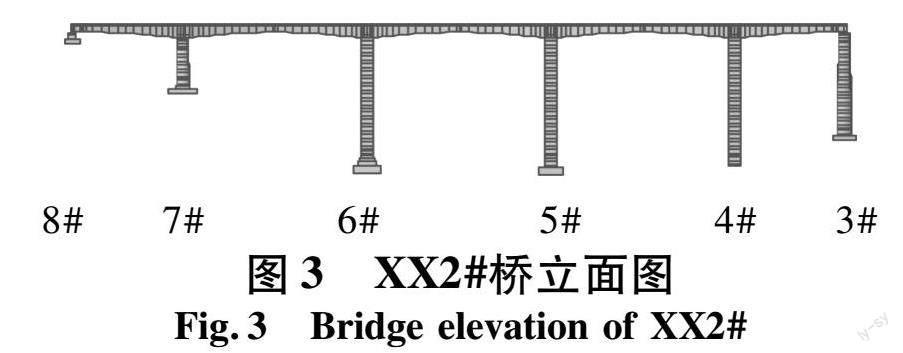
XX2＃桥为5跨刚腹板T型连续刚构体系。从左至右分别为8＃墩（连续墩），7＃墩高25 m（连续墩），6＃墩高63.5 m（刚墩），5＃墩高69.5 m（刚墩），4＃墩高69 m（刚墩），3＃高58 m（连续墩）。跨径布置为（54+3×90+54）m，具体如图１所示。

2.2 设计资料和参数标准

墩身截面均采用矩形空心墩，箱体采用单箱单室箱梁。腹板采用钢腹波纹板结构，根据受力要求，由腹板上下采用S-PBL加焊钉联结。顶板横向预应力钢束采用2φ15.2和3φ15.2钢绞线。钢绞线标准强度 f tk =1 860 MPa，采用扁锚，单向交错张拉。梁底曲线为二次抛物线，其抛物线方程为 Y=－0.002 853 745 541x2 。

2.3 施工标高计算结果

在大桥悬臂施工过程中，由于误差影响，施工阶段观测点的标高与理论计算值有一定的偏差，因此需要采取必要的方法进行调整[10]。计算前0号段悬臂施工较短误差很小，取 x 1 为0号观测点的理想计算施工抬值，并取 P  1=0。

对于 k =0即1号梁段施工标高预测调整有：

x  ^  1/0=G 1，0x  ^  0  =   1.661 00 1.563    0.0180.026   =   0.0300.041

因此1号梁段施工抬高值进一步优化为：西安方向为0.030 m，平凉方向为0.041 m。0号段预设标高分别为1 567.278 、1 567.276 m。

对 k =1 即2号梁段施工标高预测调整值有：

x  ^  k+1=x  ^  k＋1/k＋K k+1（Z k+1-x  ^  k）

本桥2号梁段预测误差协方差： P 2，1=G 2，1P 1GT 2，1，

+Q 1=Q 1=  0.0152 00 0.0152

西安方向和平凉悬臂端第2阶段预留拱度测量误差的均方差，本项目根据经验确定为 σ 1/L（1） = σ 1/R（1） =0.015；

本桥2号梁段滤波增益：

K k+1=P k+1/k（C k+1P k+1/kCT k+1+R k+1）－1

K 2=P 2，，1（C k+1P k+1/kCT k+1+R k+1）－1

西安方向和平凉悬臂端悬臂端2阶段计算误差

的均方差，本桥梁施工控制项目根据经验确定为 σ L（1） = σ R（1） =0.006；

K 2=P 2，1（P 2，1+R 2）－1=  0.0152 00 0.0152  ×

0.0152 00 0.0152 + 0.0062 00 0.0062  －1

=   0.862 00 0.862

x  ^  k+1=x  ^  k＋1/k＋K k+1（Z k+1-x  ^  k）=x  k + 1，k +K k+1 x k+1+v k+1-x  ^  k

x  ^  2=x  ^  1，0＋K 2（Z 2-x  ^  1）=x  2，1 +K 2× x 2+v 2-x  ^  1，0   =

0.0300.041  +  0.862 00 0.862    ×

0.0460.049  +  0.0060.006  －  0.0300.041    =   0.0460.053

1.46 00 1.385  =

1.46 00 1.385     0.0460.053   =   0.0670.073

所以第2階段的施工计算抬高值为1.46，1.385，最优一步预测值西安方向为0.067，平凉方向为0.073。因此1号梁段预设标高为

1 567.254 、1 567.257 m。

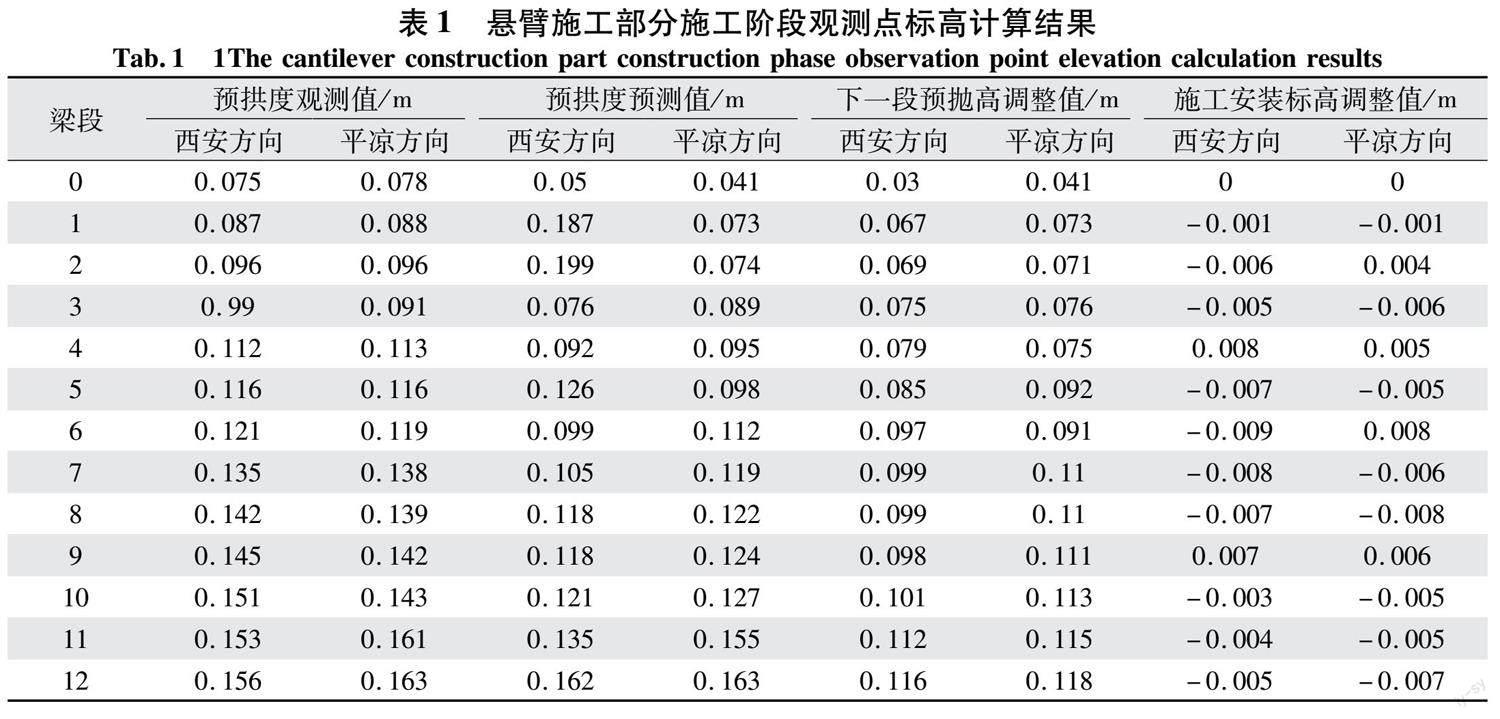
XXX2＃桥为5跨T型连续刚构体系采用悬臂施工控制，以实测参数预测施工预拱度的误差调整值，采用挂篮施工，中跨采用12段对称悬臂浇筑，边跨跨采用12段对称悬臂浇筑，跨中采用挂篮骑跨完成，边跨采用支架现浇完成，全桥对称悬臂浇筑施工结束后进行边跨合拢，然后进行次中跨合拢，最后进行中跨合拢顺序完成。严格控制施工工艺和规范施工，确保施工线形与设计相吻合。由于悬臂越长施工控制难度越大，所以施工线形控制过程中，由于篇幅有限只研究分析了西安和平凉方向6号桥墩跨中梁段各个施工阶段标高调整值。如表1所示。

由表1可知，悬臂施工12号梁段西安方向中跨合拢误差为：0.162-0.156=0.006 m；平凉方向中跨合拢误差为：0.156-0.163=-0.009 m，都符合合拢的误差要求。

从图4和图5可知，悬臂段越长，相对误差值就越大。不论是预拱度的观测值还是预测值都会随着施工推进，悬臂段的伸长，预拱度的数值明显增加。其次，抛高调整值和施工安装标高调整值也会随着增大，主要原因是悬臂段越长对温度和施工荷载、观测要求等因素越敏感，系统误差就越大，所以施工调整误差数值也会增大。

另外，从图4和图5还可以看出，施工预测数值和观测数值客观上存在一定的误差，所以采用合理的误差分析方法，合适的观测手段，准确的建模手段等因素对悬臂施工控制线形控制精度的影响至关重要；其中误差分析计算方法是弥补系统误差有效手段，尤其在大跨度悬臂施工的连续刚构桥由于分段数量较多，系统误差会随着施工阶段数量的增多对施工线形控制的精度影响越演越烈，所以必须采用合理的方法处理误差是施工控制需要的处理手段，所以采用卡尔曼滤波法在大跨连续梁桥施工控制中的应用有十分重要的作用。

3 结语

（1）气温影响主梁标高的测量放样精度，因为每天气温早上下午晚上都是变化的，每个时刻梁体混凝土的温差变化都不一致，导致测量放样时候的梁体标高和浇筑完混凝土时候的标高存在一定的差异，影响施工标高控制精度；

（2） 对于钢腹板桥梁变形收到温度的影响比较大，特别注意焊接高温影响。选择热输入低的焊接方法，如氩弧焊，控制层间温度，分段对称施焊，选用小参数的焊接规范；

（3） 悬臂段越长，相对误差值就越大，施工措施和温度对其影响就越敏感，因此对于大跨度钢腹板连续T型刚构桥采用Kalman滤波法的误差分析方法对每个施工段是十分必要的；

（4） 误差调整一方面要根据设计要求进行设计误差调整，通过先前几段施工来推算确定设计参数，根据计算模型利用软件进行确定。其次在施工误差调整中，运用Kalman滤波法的计算方法对后面的每个施工段施工误差进行合理的调整。经过监控组的认真分析和努力，大桥监控量测取得了很好效果，误差控制在合理范围内，为今后类似工程提供了很好的经验。

【参考文献】

[1]  孙宗磊，孟繁增.下穿高铁桥梁施工安全风险评估及变形动态控制技术[J].桥梁建设，2022，52（5）：135-141.

[2] 吴章华，多跨悬浇PC连续刚构桥施工阶段监测与控制研究[D].《重庆交通大学硕士论文》，2015，10-15.

[3] 王裕阳.连续刚构桥梁施工过程中的变形控制影响要素分析[J].工程技术研究，2019，4（15）：41-42.

[4] 王岩.预应力混凝土桥梁施工过程中的关键技术[J].山西建筑，2019，45（14）：126-127.

[5]  王士林，刘中仁，赵秀运.核电站钢制安全壳底封头拼装方式与焊接变形控制[J].电焊机，2019，49（4）：244-249.

[6] 万宇，曾春红.桥梁工程结构施工过程中的变形控制[J].交通世界，2017（32）：102-103.

[7] 種永峰.影响连续刚构桥梁施工过程中的变形控制要素分析[J].福建交通科技，2018（6）：77-79.

[8] 刘建明.桥梁工程结构施工变形控制质量研究[J].交通世界，2018（23）：101-102.

[9] 郭涛，刘红征.盾构隧道穿越既有桥梁施工变形控制[J].市政技术，2018，36（1）：101-104.

[10] 任全勇，张林江，冯子哲.大跨度桥梁结构施工中的变形控制处理[J].科技与创新，2018（1）：128-129.